高陡边坡形态对边坡稳定性的影响分析

2021-09-02刘正宇王飞飞王少林

中国钨业 2021年2期

马增，刘正宇，邹平，王飞飞，王少林

（1.长沙矿山研究院有限责任公司，湖南长沙 410012；2.国家金属采矿工程技术研究中心，湖南长沙 410012）

影响边坡稳定性的因素有很多，比如边坡工程地质条件、边坡高度、边坡下的空区、边坡角度、降雨、边坡的几何形态和暴露时间等[1-5]。在这些因素中，边坡的工程地质条件、边坡高度、降雨和暴露时间都无法进行人为的控制，与边坡所处位置和条件存在直接关系。然而边坡几何形态是后期工程师综合考虑各种条件后进行确定的，这其中必然会掺杂各种主观因素，但对于何种边坡形态才是最优的边坡几何形态，需要深入探究[6-9]。

马力等[10]为了研究平直边坡和凹形边坡的内部机理，建立了两种边坡形态的力学模型，论证了不同边坡形态对应的力学结构的差异，得到了凹形边坡能够缓解应力集中，稳定性优于平直边坡。马永志等[11]利用FLAC3D软件计算了不同滑动面几何形态下的边坡安全系数，结果表明，影响安全系数最大的是滑动面上下折线的倾角。杨金林[12]利用轴比来定义边坡形状，当边坡坡面为凹形边坡时，边坡高度不变，安全系数会随着轴比增大呈现先增大后减小的规律，且当轴比为1/3 时安全系数最大。

以上研究成果对于边坡几何形状对边坡稳定性的影响以及力学机理已经进行了详细的论证。但在实际边坡设计时通常将边坡分为上下两段且采用不同的边坡角，那么凹形边坡和凸形边坡的选择以及布置上下段转折点适当位置仍然并未做过多研究，本研究就这些问题进行探究，揭示边坡形状对边坡稳定性的影响规律，对上下段转折点位置的布置提出建议。

1 概述

1.1 分析模型

分析模型是进行边坡极限平衡计算的基础，也是与计算机交互的语言。合理的模型几何尺寸有助于精确的计算边坡安全系数，使得到的边坡安全系数与实际情况一致，在合理边坡模型尺寸研究方面前人已经开展了大量的工作，且每个岩土分析软件公司也对分析模型的尺寸进行了规定，此次边坡模型采用国际通用的标准模型尺寸，如图1 所示。

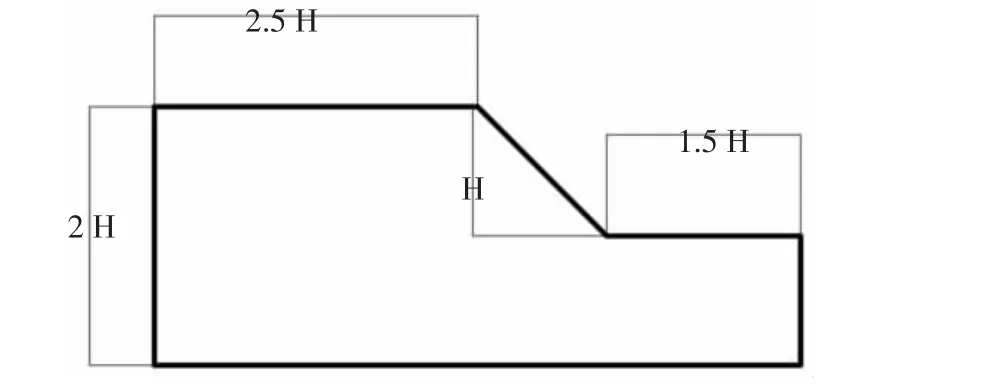
图1 合理边坡分析模型几何尺寸示意图Fig.1 Schematic diagram of geometric dimensions of reasonable slope analysis model

针对高陡边坡，边坡高度应大于300 m 且小于或等于500 m，边坡角度为40°～50°，此类边坡多为露天采场边坡。本研究分析论述的对象为高陡边坡，边坡高度设计为300 m，整体边坡角设计为45°。

1.2 岩体力学参数

岩体力学参数是直接反映边坡岩体强度质量的关键数据，也是极限平衡分析的基础。本研究分析不以某个具体矿山或某一种具体岩体为主，而是按照《非煤露天矿边坡工程技术规范》中对高边坡（I 级边坡）安全系数的要求为主，即在一面坡时边坡的安全系数大于1.25，进行反算得到边坡的岩体力学参数[13]，见表1。

表1 分析岩体力学参数表Tab.1 Analysis of rock mass parameters table

1.3 边坡形态分布

边坡形态是影响边坡稳定性的因素之一，在矿山的实际生产中影响边坡几何形态的主要因素有边坡稳定性、采矿经济指标、矿体形状及分布等。本研究分析的边坡形态是将高300 m、边坡角45°的边坡分为上下两段，通过改变边坡上下分界转折点位置来调整边坡形态。

固定边坡高度和整体边坡角，将边坡面以坐标网形式表示，每个网格20 m×20 m，通过改变上下段的转折点位置来调节边坡几何形态，根据矿山生产的实际情况，剔除极端的情况，剩下图中红线圈内部分，见图2 将图中红线圈出有效的点进行编号，坡顶处为1，坡脚处为68，每一个编号代表一种边坡形态。

图2 边坡形态分布Fig.2 Slope shape distribution map

2 分析结果

边坡的极限平衡分析应用Slide6.0 软件自动搜索边坡滑面，采用简化Bishop 法对不同编号边坡进行计算，得到了相应编号的安全系数，这些数据符合边坡的实际规律，计算结果见表2，图3。

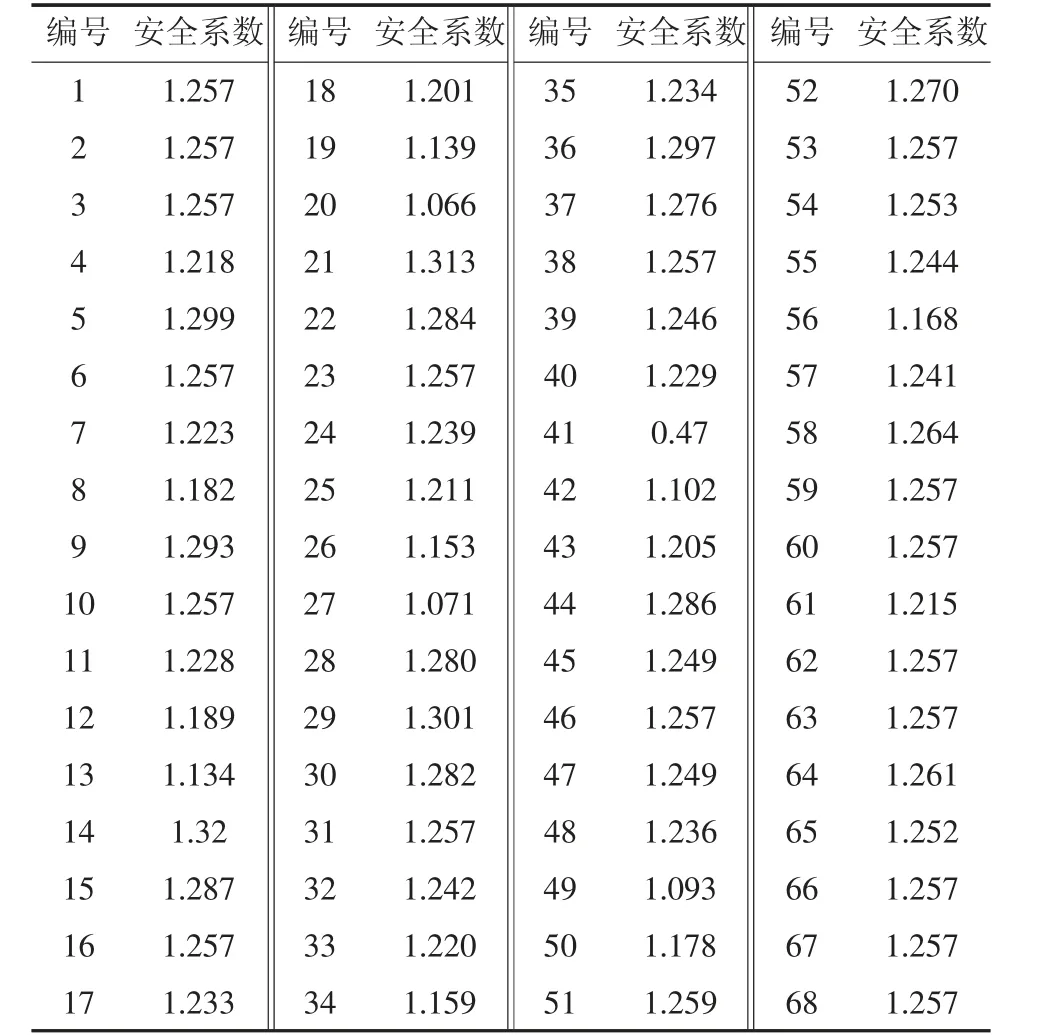
表2 计算安全系数结果Tab.2 Calculation results of safety factor

图3 简化Bishop 法边坡安全系数分析结果Fig.3 Analysis results of simplified Bishop method slope safety factor

从得到的安全系数可以看出：数据整体呈现规律性波动；最大安全系数出现在编号28 到30 之间，最小安全系数为编号41，其次是编号20；编号41 边坡通过对滑面进行检查发现，软件自动搜索到局部边坡安全性较低。

3 计算结果对比分析

3.1 凹形边坡和凸形边坡对比分析

凹形边坡和凸形边坡是相对于平直边坡相比较而言的，主要反映的是边坡基本形状。本次分析中凹形边坡和凸形边坡编号均有26 个，通过对这两大类52 种不同形态的边坡进行计算，得到了凹形边坡和凸形边坡的安全系数关系，见图4。

图4 凹、凸形边坡安全系数对比Fig.4 Comparison of safety factors of concave and convex slopes

从结果可以看出，在边坡转折点在160 m 以上时，凹形边坡的安全系数明显大于凸边坡的安全系数，但边坡转折点在160 m 以下时，凹形边坡的安全系数并不占优势，且边坡上部角度越陡边坡安全系数越低；与平直边坡相比，凹边坡中安全系数大于平直边坡安全系数的有16 个，凸形边坡中安全系数大于平直边坡安全系数的有2 个；因此从计算结果可以看出凹形边坡的安全系数要大于凸边坡的安全系数，在工程中采用凹形边坡比凸形边坡稳定性会更好。

3.2 同水平不同边坡形态的对比分析

在实际生产中，边坡的转折点位置是根据边坡岩体风化程度、岩性界线、矿体边界以及实际的需要而定的。在边坡高度和边坡角不变的条件下，边坡的稳定性与边坡转折点的位置有关，即与边坡形态有关。安全系数云图见图5。

从图5 可以看出在160 m 以上随着边坡转折点位置不断向右移动，安全系数逐渐减小，在160 m 以下随着边坡转折点位置不断向右移动，安全系数逐渐增大；通过计算得到的数据和图表可以看出，最优的边坡转折点位置应当布置在边坡中部靠上部位，即边坡的1/2～2/3 处。

图5 安全系数云图Fig.5 Safety factor cloud atlas

3.3 同垂直位置不同边坡形态的对比分析

同一垂直位置即在边坡上x 值不变，从对边坡形态的描述应当是x 值不变，随着y 值不断增大上部边坡由陡变缓，下部边坡由缓变陡。

从图5 分析结果来看，安全系数总体呈现为由小变大再由大变小的趋势，即靠近平直边坡安全系数较大，反之远离平直边坡安全系数较小。同时通过分析可以看出当x 值小于100 m 时，即小于边坡长度的2/3，呈现的细节有所变化，边坡的安全系数在未到达平直边坡处达到了最大值，而当x 值大于120m时，边坡的安全系数最大值在平直边坡处出现。