基于RecurDyn的4旋翼摆臂式清洗机器人设计

芦红利， 闫 娟

(上海工程技术大学 机械与汽车工程学院， 上海 201600)

爬壁机器人作为极限作业机器人中的一个重要结构分支，在桥梁检测、高楼建筑的外墙清洗等领域具有广阔的应用前景[1]。工作中，爬壁机器人在安全吸附的情况下，实现快速、平稳地移动，而且要对凸起、凹坑和交叉面等复杂的壁面情况做出即时、有效的应对，也是当今爬壁机器人研究领域的热点之一[2-3]。

国内外关于爬壁机器人如何进行高效越障和吸附做了长期的研究[4-5]，杨春等[6]针对如何越过壁面障碍物，设计了串联式轮足复合式爬壁机器人，通过机器人的2足交替抬起实现对障碍物的跨越，但该机器人越障效率低，越障控制复杂；董寒等[7]研制的十字框架爬壁机器人，通过固定在框架上的真空吸盘交替吸附壁面进行移动，其运动缓慢且无法跨过较高的障碍；冯伟博等[8]研究了仿尺蠖爬壁机器人，该机器人具备越障能力，但因为双足跨越式的越障方式，越障和移动速度较慢。采用吸盘方式的BPIPED式关节机器人，可以完成空间内的移动和越障，但吸盘负载能力有限，无法提供稳定的作业平台；潘雷等[9]提出依靠真空泵产生负压完成吸附的功能，但是当吸附壁面环境复杂，壁面凹凸不平时，吸附的稳定性大大下降；陈月强[10]设计的磁吸附履带式攀爬机器人，可以实现吸附和移动功能，但是由于磁吸附使用环境限制，在越障方面的能力较差。

针对目前爬壁机器人在越障方面控制复杂、运动不连续的问题[11]，基于地面摆臂式机器人攀爬障碍物原理，课题组设计了一种基于旋翼的摆臂式爬壁机器人，对机器人越障过程进行运动学分析，研究了旋翼电机输出转矩和壁面角度变化的关系，仿真实验对所设计的机器人越障性能进行验证和分析，为爬壁机器人实际开发应用和控制系统的设计提供了参考依据。

1 机械系统设计

机械系统的三维模型如图1所示，由推力机构、摆臂机构、行走机构、车体等组成。为了实现机器人越障及多变化姿态， 2个摆臂均可进行360°旋转。机器人主要由 7个电机驱动，其中4个驱动旋翼叶片，2个驱动机器人的左右主履带，1个驱动左前摆臂机构和右前摆臂机构的共同运动。机器人上层布置的旋翼提供机器人向上行进和越障过程中所需要的吸附力，同时，2个摆臂机构通过套筒轴连接，使得2个摆臂机构的旋转运动和2个主履带系统旋转运动互不干涉，从而实现机器人在行进过程中对自身的姿态进行调整。

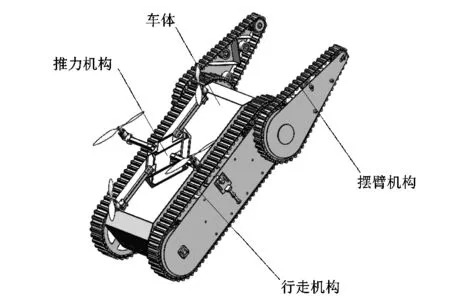
图1 爬壁机器人造型Figure 1 Wall-climbing robot modelling

爬壁机器人前端与牵引绳索连接，通过外接电缆来提供机器人所需的电力，使得机器人运行更加平稳具有更大的承载能力，机器人可根据实际需求，扩展相应的模块，如激光测距仪、摄像头、红外线热成像仪、清洗模块和机械手等，以满足不同环境下，勘察、清洗墙壁、救援和反恐等不同工作的需求，机器人基本参数如表1所示。

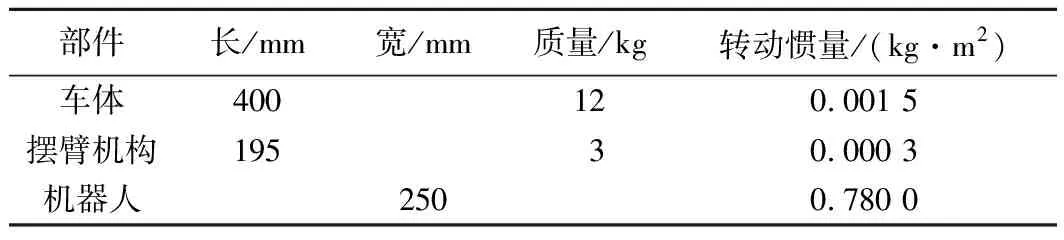
表1 爬壁机器人结构参数Table 1 Structural parameters of wall-climbing robot

2 爬壁越障性能分析

2.1 机器人的质心分布

如图2所示，以机器人的履带后轮轴心为原点，建立坐标系xO1y，前后履带轮轴心O1和O2的距离为l0，主车体质心G1坐标为(l1,h1)，机器人主车体的质量为m1，越过障碍物时，需要2摆臂同步旋转，设2个摆臂的质量为m2，摆臂质心为G2，并处于2摆臂的中心线O2O3上，履带前带轮轴心距摆臂质心G2的长度为l2，假设摆臂的2个履带轮轴心的距离为l3，2摆臂与壁面的夹角均为θ，且θ∈[0,2π]，假设机器人的宽度为b，主履带的带轮的半径为R，摆臂履带轮的半径为r，都包含履带的宽度，则机器人质心G(xG,yG)的坐标为：

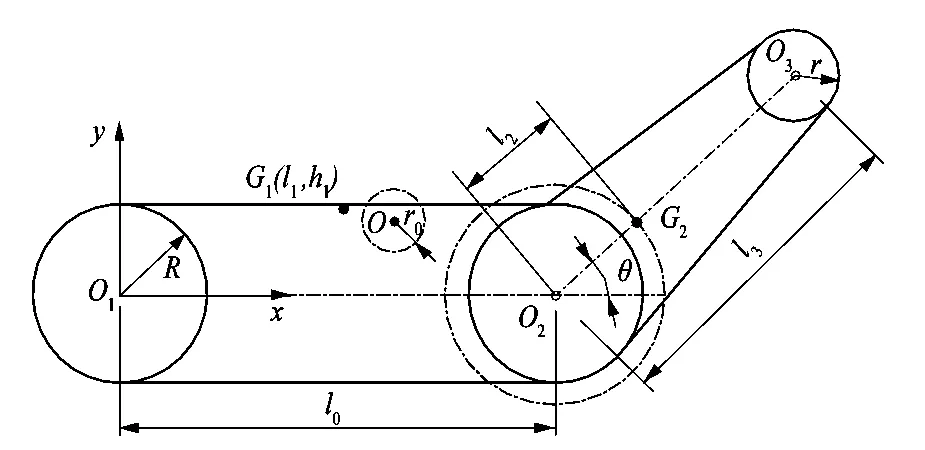
图2 机器人质心运动轨迹Figure 2 Trajectory of center of mass of robot

(1)

机器人的质心满足以下的关系式：

(2)

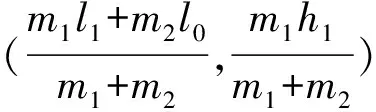
2.2 机器人越障能力分析

爬壁机器人攀爬障碍物的过程如图3所示。当前方有障碍物出现，摆臂机构的电机驱动机器人双摆臂逆时针旋转，使得摆臂前端高于障碍物；然后在履带的驱动下，行走机构的主履带搭靠在障碍物的外角线上，在行走机构电机推动下，机器人继续向前移动，摆臂机构的电机驱动摆臂顺时针转动；当机器人的重心越过障碍物的外角线，机器人以此点为支点，顺时针旋转，成功攀爬上障碍物。

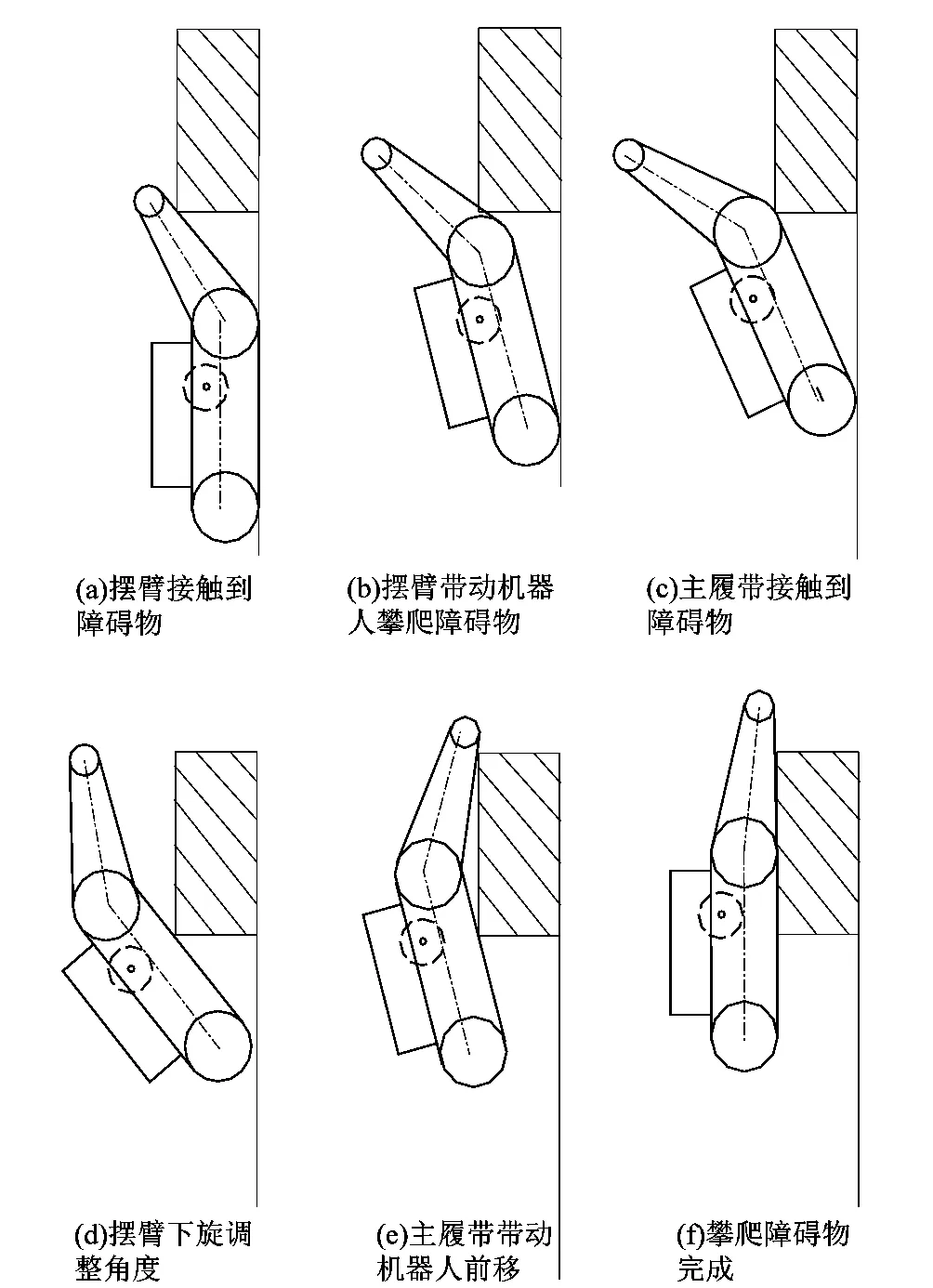
图3 机器人攀爬障碍物过程Figure 3 Process of robot climbing obstacles

图4为机器人质心恰好跨越障碍物时外角线的状态。当机器人质心为机器人质心轨迹与障碍物外角线的垂线相切的切点时，最有利于机器人攀越障碍物。当机器人的双摆臂处于水平状态时，机器人攀爬的障碍物高度为最大值。此时，机器人的仰角α和双摆臂的摆臂角度θ关系为α+θ=2π。

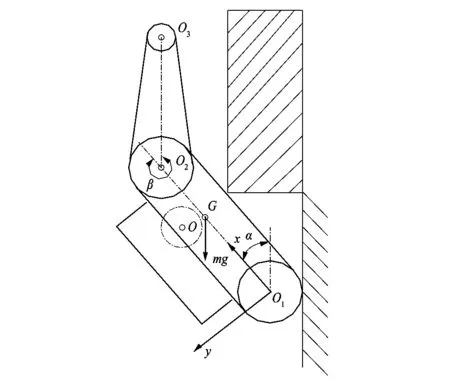
图4 攀爬障碍物时机器人质心 跨越障碍物外角线Figure 4 Center of mass of robot crosses outer corner of obstacle when climbing obstacles forward

(3)

式中：R为主履带的带轮半径；α为机器人的仰角；θ为双摆臂的摆臂角度；H为障碍物高度；l为机器人质心的横坐标；h为机器人质心的纵坐标。

将l=xG,h=yG代入式(3)，得到此机器人最大攀爬的障碍物高度Hmax(θ,α)。

(4)

3 爬壁机器人动力学分析

爬壁机器人动力学性能必须满足2个条件：①爬壁机器人能够在壁面完成行进和越障的功能；②爬壁机器人在行进过程中保证不会发生滑移、机器人本体反转倾覆等失效形式。

为了实现机器人在壁面平稳运行，如图5所示，旋翼电机的输出转矩MD必须克服牵引力产生的转矩ML，以及推力机构产生的吸附力F1和支持力形成的转矩MX和重力转矩MG的作用，即满足下式：

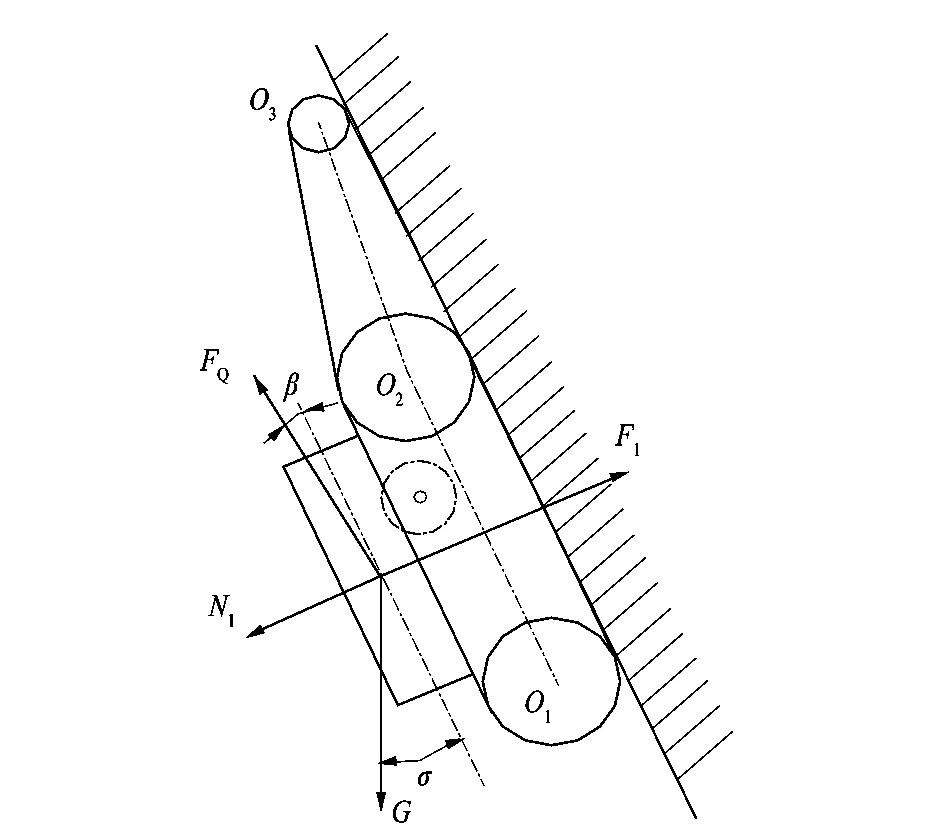
图5 机器人爬行模型Figure 5 Robot crawling model

(5)

式中MD为旋翼电机输出转矩。

壁面存在倾角，绳子拉紧时，机器人本体会产生一定的角度，因此使得推力机构产生的吸附力不等于所需要的吸附力。

ML=FQl1cosβ;

(6)

MG=GH1cosσ。

(7)

式中：G为机器人受到的重力,l1为绳索和壁面之前的距离，β为牵引力和壁面之间的夹角，H1为重心和壁面之间的竖直距离，σ为壁面和竖直平面的夹角，FQ为卷扬机提供的牵引力。

(8)

MX=N1h1。

(9)

式中：FG为反作用力，h1为吸附力和支持力之间的距离。

根据式(5)～(9)，可得机器人在攀爬过程中所需旋翼电机输出力矩：

FQl1cosβ。

(10)

4 越障运动的仿真和越障高度理论值计算

4.1 越障能力计算

机器人攀爬障碍物时机器人的主要参数为：R=60 mm，r=30 mm，l0=310 mm，l2=100 mm，l3=170 mm，m1=12 kg，m2=3 kg。以上参数代入式(2)和(4)中，当仰角和摆臂摆角分别在(0°，60°)和(0°，360°)范围取值时，可得H的最大值Hmax=178.6 mm。

4.2 机器人仿真测试

为了验证机器人越障高度，针对高度不同的矩形障碍物进行仿真，探究机器人攀爬障碍物高度最大值。

通过RecurDyn进行仿真验证，机器人越障仿真如图6所示，针对175 mm、180 mm与185 mm的不同高度障碍物进行分析表明：在通过175 mm障碍物后，机器人能够相对快速恢复到稳定的状态；越过180 mm障碍物后，机器人的重心的位移波动持续较大，但最终还是能够恢复到稳定的状态；当障碍物的高度调整为185 mm时，机器人无法进行越障。经过多次仿真实验确定机器人的最大越障高度为180 mm。图7为机器人攀越不同高度障碍物的重心高度与时间的关系，实验表明：机器人旋翼推力机构的吸附性能良好，机器人能够平稳地在壁面完成爬行和越障的功能。

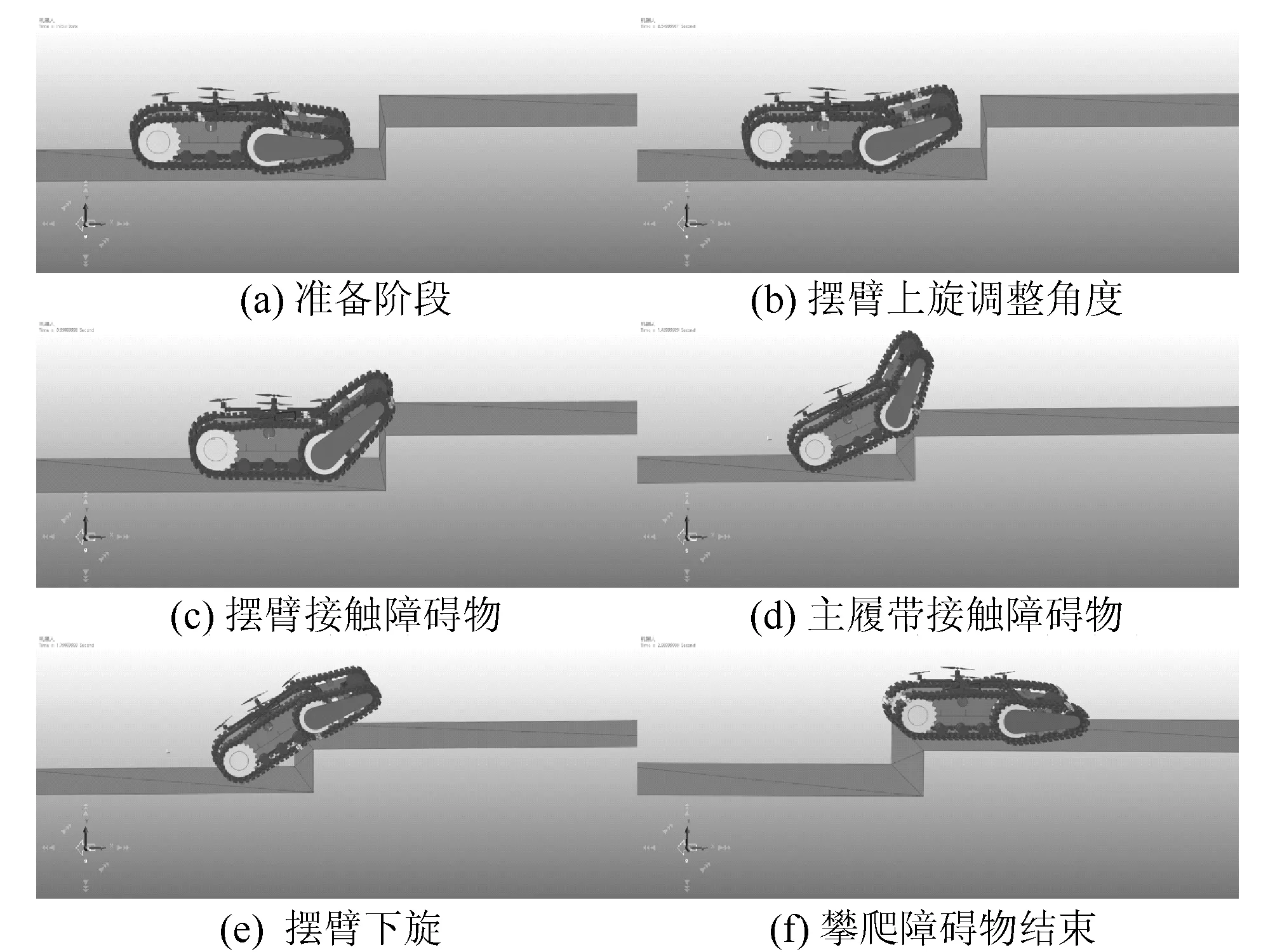
图6 虚拟样机攀爬障碍物过程Figure 6 Process of virtual prototype climbing obstacles

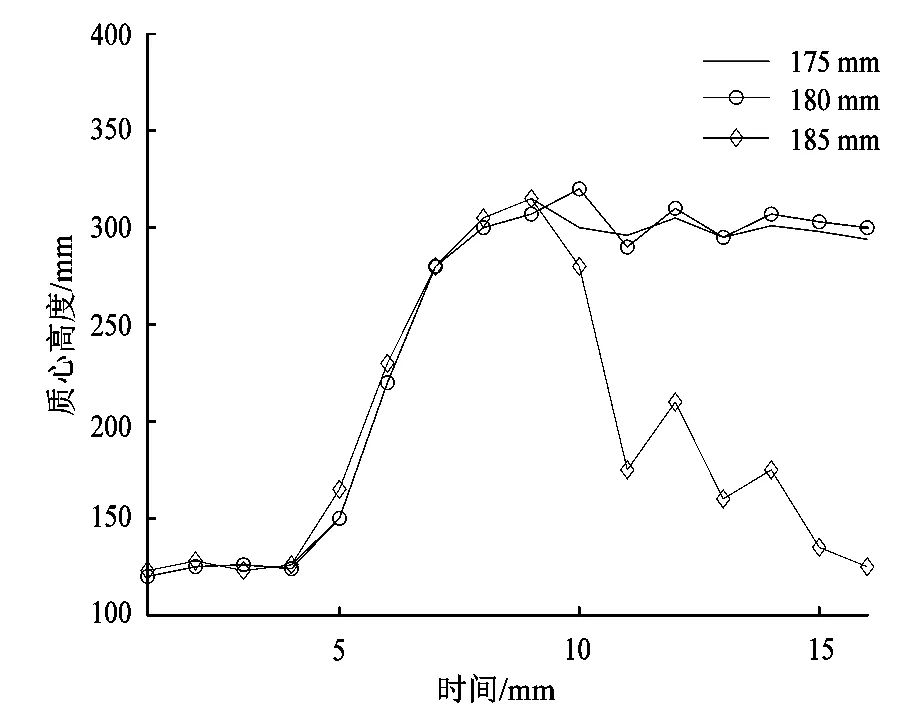
图7 机器人攀越障碍物重心高度与时间关系Figure 7 Relationship between height of center of gravity of robot and time when robot climbing obstacles

5 结论

课题组为解决现有爬壁机器人在越障方面动作不连续和越障效率低的问题，研究了柔性摆臂越障机构，并在机器人的运动过程中，从运动学角度，研究了双履带摆臂机器人的越障原理。利用摆臂的摆动，使得机器人的质心越过障碍物的关键边界线。

课题组从运动学角度分析机器人攀爬障碍物时的运动机理，并建立了机器人壁面攀爬的运动学模型，计算出机器人在不发生失效形式下旋翼电机理论输出转矩，并通过仿真实验，验证了机器人的旋翼的吸附性能，以及攀爬障碍物的能力。在此基础上，课题组设计了一种基于旋翼的摆臂式爬壁机器人，为爬壁机器人的实际开发应用和控制系统的设计提供基础。