基于CFD的不同搅拌组合多相流流场研究
2021-09-02姚晨明石秀东彭晶鑫
姚晨明, 石秀东, 彭晶鑫
(1.江南大学 机械工程学院, 江苏 无锡 214122;2.江南大学 江苏省食品先进制造装备技术重点实验室, 江苏 无锡 214122)
在气液搅拌釜内,流体动力学环境主要由通气条件、搅拌转速和湍流组成[1]。通过搅拌输入机械能,让整个发酵过程获得持续稳定的流场、动量、能量及物质传递,从而使相关生物化学反应稳定地进行,达到预期的发酵效果[2]。合理的搅拌釜结构设计能够在发酵过程中为目标产物生产菌种提供一个有利于其生长繁殖的流体动力学环境。在对搅拌釜进行设计的初期,往往都是结合经验关联式通过试验的方式进行,这样的方式存在研发成本高、研发周期长等问题[3]。因而,CFD数值仿真技术已经成为生物反应器研究中减少研发时间和成本、进行反应器优化及放大设计的重要手段[4-5]。
谢明辉等[6]在不同溶液中通过CFD数值仿真技术与实验流体力学相结合的方式进行气液两相流研究。研究发现气液传质性能依赖于桨型结构形式,不同桨型结构产生不同的流场。桨型结构与物性一起决定了气泡的动力学和传质性能。曹毅等[7]对实验室用搅拌釜进行气液两相流数值模拟研究,发现单桨叶搅拌釜提供的流场环境难以满足聚赖氨酸微生物发酵的需要,于是采用增加桨叶数目和桨叶类型对此问题进行了优化。Wang等[8]对不同工况下多相系统的重要水动力参数,如体积平均总气持率和时间平均局部气持率、轴向液速等进行了详细的模拟和分析,进一步预测了气泡的尺寸分布,揭示了气相的独特性质。
课题组以气液搅拌釜为研究对象,利用CFD技术进行气液两相流非稳态求解,探究多种搅拌组合下搅拌釜内流场特性以及能耗情况,为发酵设备中搅拌器的设计及优选提供参考。
1 数值模拟方法
1.1 物理模型
该搅拌釜主要由带挡板的3层搅拌桨和椭圆封头的筒体组成。筒体底部装有环形气体分布器,气体分布器的气体出口向下。考虑到该模型的复杂性以及气液两相流模拟时对网格质量的要求较高,对该模型进行了简化处理,具体见图1所示。不同的搅拌桨组合,对微生物发酵性能有很大影响,会影响最终产物的产量。同时,多层搅拌时,底桨是气液分散性能好坏的关键[9]。课题组选取6直叶圆盘涡轮桨(RT-6)、6叶半圆式圆盘涡轮桨(CD-6)、下推式45°的4斜直叶桨共3种桨型组成的4种3层搅拌组合进行模拟,搅拌组合见图2所示,旋转方向为顺时针旋转,模型具体结构参数见表1。
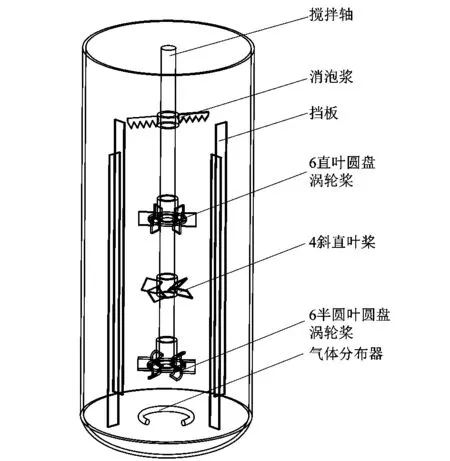
图1 搅拌釜简化模型Figure 1 Simplified model of fermentation tank

图2 搅拌组合简化模型Figure 2 Simplified model of mixing combination
1.2 控制方程
课题组使用Eulerian-Eulerian双流体模型来模拟计算气液两相流问题,不考虑温度及模拟物料的化学反应,因此忽略组分运输项和源项,简化的气液两相流连续性方程如下:

(1)

表1 模型主要结构参数
式中:φm表示m相的体积分数,即∑φm=1;ρm为该相的密度值,kg·m-3;um代表该相的速度,m·s-1;m代表液相(l)或气相(g)。
动量方程如下:
-φmp+·(φmτeff,m)+φmρmg+Fex,m+Mm。
(2)
式中:Fex,m为相间作用力,N;Mm表示主相与次相间由于湍流和相对运动等因素造成的动量交换,kg·m·s-1;p为所有气液相共享的压力,Pa;φm,ρm,g为气液相所受重力,N。
τeff,m为第m相的压力应变张量,其表达式如下:
(3)
式中:λm和μm是m相的剪切和动力黏度,N·s·m-2;I为单位张量。
在气液两相流中,曳力是气液两相间的主要作用力,对于本研究的气液两相流问题采用Kolev等[10]提出的曳力系数模型,在FLUENT中被称为通用曳力模型(universal drag)。该模型广泛适用于包括非球形气泡等各种气泡流的气泡变形情况下的气泡曳力计算,其计算公式如下:
(4)
(5)
式中:CD表示气液相间曳力系数;Ad为气泡横截面积,cm2;ρl表示液相密度值,kg·m-3;Re为雷诺数;ug和ul表示气相及液相的速度,m·s-1。
在气液两相流中由气泡径向分布以及液相湍动引起的力叫做湍流扩散力。这种力的作用是使气泡在径向上分布得更加均匀,其计算公式如下:
(6)
式中:CTD为湍流扩散系数;CD为气液两相间的曳力系数;δt为湍流Schmidt数;υt为亚网格黏度,m2·s-1;φg和φl表示气相及液相的体积分数。对于本课题气液两相流问题采用Burns-et-al模型[11]。
1.3 网格划分
课题组在模拟过程中采用FLUENT Meshing划分多面体网格。多面体网格在划分复杂模型时相较于非结构化自由四面体网格具有更高的精度,而其数量只有四面体网格数量的1/5~1/3[12]。以搅拌组合A为例,取模型上桨叶周围一点的液相速度,以及总搅拌功率作为指标,考察了3种不同网格数量对液相速度分量以及搅拌功率的影响,具体如表2所示。从表2中可以看出随着网格数量的增加,该点的液相速度值和搅拌桨的搅拌功率值逐渐趋于平稳,模拟结果几乎接近,同时考虑到计算机资源和模拟时间等因素,最终选取86.31万左右的网格数量。不同的搅拌桨组合,划分的网格数量有所偏差,课题组选取的网格数量基本维持在86万左右,对最终模拟结果影响不大。

表2 网格无关性验证结果Table 2 Grid independence verification results
1.4 计算条件
课题组采用ANSYS FLUENT软件进行数值仿真。气液两相流模拟时采用滑移网格模型法(SM), Eulerain-Eulerain双流体模型,湍流模型选择RNGκ-ε模型,进行瞬态求解。求解过程中监测整体气相体积分数和搅拌轴力矩系数变化,当气相体积分数以及力矩系数不再发生明显变化且趋于稳定时,停止求解,此时得到的结果即为最终结果。求解时采用单一气泡模型,设定气泡直径为2 mm[6-7]。Khopkar等[13]研究发现气液搅拌釜主体区域中虚拟质量力和升力影响较小,因此气液两相之间的作用力不考虑升力和虚拟质量力的影响。曳力模型采用universal drag模型,湍流扩散力模型采用Burns-et-al模型。
模拟物料选取空气和水。具体参数:水的密度为998.3 kg·m-3,黏度为1.00×10-3Pa·s;空气的密度为1.225 kg·m-3,黏度为1.79×10-5Pa·s。模拟工况为通气量1.3 m3·h-1,转速850 r·min-1。
2 结果与讨论
2.1 速度场
图3为相邻2挡板中间平面上通过数值模拟得到的液相速度云图(左)与矢量图(右)。
通过观察图3的速度云图发现组合B和组合D整体区域速度分布不均匀,低速区域范围较大,特别是上桨叶上方区域整体速度偏小,不利于物质的传递与混合,高速区域主要集中在桨叶叶端附近以及桨叶下方;搅拌组合A以及组合C整体区域速度分布相较于组合B和D来说更加均匀,低速区域范围较小,整体的流动混合效果较佳,物质传递效率较好,高速区域主要分布在桨叶叶端周围。

图3 液相速度云图及矢量图Figure 3 Liquid phase velocity cloud diagram and vector diagram
如图3的速度矢量图所示,搅拌组合A和C的右半部分共有4个循环区域。上桨和底桨都是径向流搅拌桨,其产生的径向流首先射向壁面,然后向上或者向下流动,形成典型的径向双循环流动,与孙东东等[14]描述一致。同时由于中间轴向流搅拌桨的存在,可以看到上桨的下循环区域与底桨的上循环区域之间存在流动交换,这样有利于循环与循环之间的物质传递。搅拌组合B和D的右半区域共有一大一小2个明显的循环区域,而上桨叶上方区域未见明显的循环区域。大循环区域主要位于上桨叶与底桨叶之间,其产生是由于径向流底桨在上桨及中桨形成的轴向循环区域发生了合并从而形成了大循环区域。
图4(a)~(c)为液相速度在不同高度处的径向特征线上的分布情况。截取径向特征线Z1研究搅拌釜上桨和中桨之间区域流动混合情况;截取径向特征线Z2研究搅拌釜中桨和底桨之间区域流动混合情况;截取径向特征线Z3研究搅拌釜釜底区域流动混合情况。从图中可以看出,在3个不同高度Z1=310 mm、Z2=190 mm、Z3=72 mm的径向特征线上,4种搅拌组合的液相速度的方向分布规律都与其矢量图一致。在Z1=310 mm处搅拌组合B和D的液相速度在搅拌桨附近区域相比于组合A和C大,然而在靠近壁面处却相反,说明在上桨位置采用径向流搅拌桨能够为附近流体提供很好的径向流动,避免釜内壁面附近的物质无法参与循环交换。但是在上桨与中桨之间提供的流体轴向循环速度并不能与轴向流搅拌桨相比。在Z2=190 mm处,整体上搅拌组合B和D的液相速度较大,这是因为上桨及中桨都采用了轴向流搅拌桨,使其提供了较大的轴向循环速度。在Z3=72 mm处,以6直叶圆盘涡轮桨为底桨的组合A和B的速度变化规律相似且速度大小相差不大。同样地,以6半圆叶圆盘涡轮桨为底桨的组合C和D速度变化规律相似且速度大小相差不大。
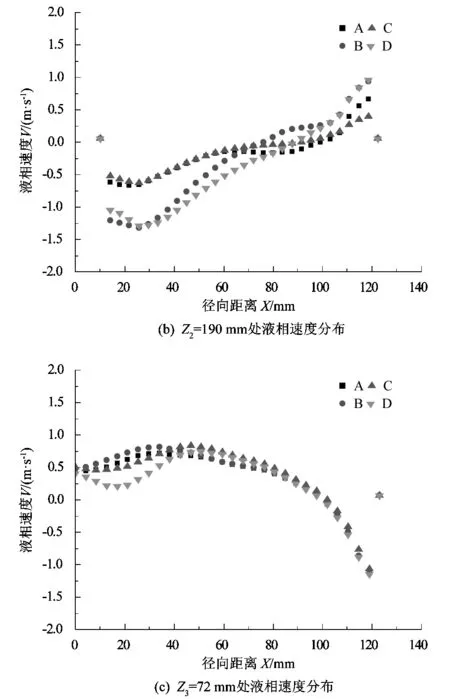
图4 液相速度径向分布图Figure 4 Radial distribution diagram of liquid phase velocity
从速度场的分析来看,上桨和中桨采用轴向流搅拌桨形成的流场会得到较大的轴向循环速度,但是速度过于集中在桨与桨之间的区域,而上桨采用径向流搅拌桨后形成的流场整体速度分布较均匀,没有过于集中的高速区域,更适合于釜内物质的整体循环混合和传递。
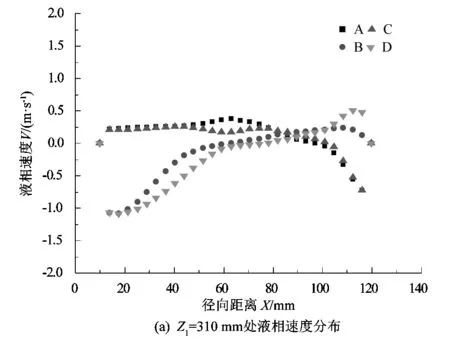
图5所示为液相速度在不同高度处特征线上的分布示意图。

图5 特征线示意图Figure 5 Schematic diagram of characteristic line
2.2 气相体积分数
图6为气相体积分数在相邻2挡板中间平面上的分布情况。从图6中可以看出:不同搅拌组合所产生的流型不同,气体分布情况也不同。釜内气体在每层桨附近及循环区域内部,气相体积分数明显高于其他区域。结合图3液相速度云图以及矢量图的分析可以知道导致这种现象的原因是桨叶后方压力低,在压差的作用下,气泡从高压区向低压区运动,使得气泡容易在该区域内聚集,同时搅拌桨所形成的循环涡使得气体在循环区域内滞留时间延长,增加了该区域的气相体积分数。而底桨由于采用了圆盘式的结构设计,使得在底桨下方区域聚集了大量气体,气相体积分数高。

图6 气相体积分数轴向分布Figure 6 Axial distribution of gas volume fraction
图7为底桨附近横截面上的气相体积分数分布云图。从图7中可以看到:6直叶圆盘涡轮桨的桨叶后方有气泡堆积区域,形成了较大的气穴,而6半圆叶圆盘涡轮桨桨叶后方的气体堆积区域较少,形成的气穴并不大[15],而其搅拌区域周围气体分布更均匀一些,平均气相体积分数也高于6直叶圆盘涡轮桨的搅拌区域。
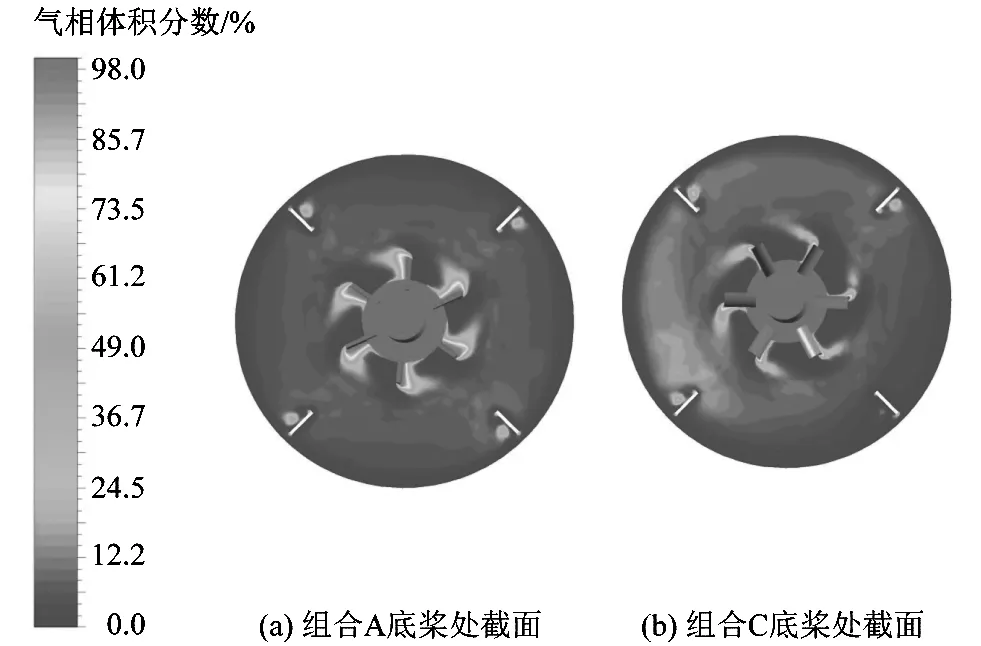
图7 横截面气相体积分数分布云图Figure 7 Cross-sectional gas volume fraction distribution cloud map
综合上述分析可以知道:整体上,搅拌组合A和C的气体分布比搅拌组合B与D的更均匀一些,有利于好氧微生物的发酵;6半圆叶圆盘涡轮桨相比于6直叶圆盘涡轮桨在径向上的气体分散性能更好一些,能使气体有效地扩散到周围,更加均匀地分布。因此总体上搅拌组合C的气液分散效果更好一些。
2.3 通气搅拌功率
表3给出了各搅拌组合通过数值模拟以及实际试验得到的通气搅拌功率。

表3 通气搅拌功率Table 3 Aeration mixing power
表3中搅拌组合A和C分别由2个径向流桨和1个轴向流桨组成,而搅拌组合B和D分别由2个轴向流桨和1个径向流桨组成。从表中可以得到通气搅拌功率大小顺序为组合A>组合C>组合B>组合D。再结合各搅拌组合选用的桨型,又可以知道在相同的工况和结构参数下,径向流搅拌桨的功率要比轴向流搅拌桨大,6直叶圆盘涡轮桨的功率要比6半圆叶圆盘涡轮桨大。模拟结果与试验测得的结果基本相符,误差率在可接受范围内。同时数值模拟得到的搅拌功率要比实际工作时的搅拌功率偏小,偏小的原因是数值模拟时未考虑流场中存在的固体区域以及其他阻力等因素。
3 结论
课题组基于CFD技术采用滑移网格模型法(SM)研究了气-液两相流下不同搅拌组合的非稳态流场特性,得到了以下结论:
1) 在相同工况条件下,不同的搅拌组合形成的流场特性有很大区别。上桨采用径向流桨的搅拌组合形成的混合流场整体速度分布更均匀,没有过于集中的高速区域,更适合于釜内物质的整体循环混合和传递。同时上桨和底桨采用6半圆叶圆盘涡轮桨的搅拌组合C气液分散性能更好一些。
2) 总的功耗方面,搅拌组合A>组合C>组合B>组合D。
课题组的研究对发酵设备中搅拌器的设计及优选有重要的参考价值。
