阶梯钻钻削AISI4340的轴向力和刀具温度研究
2021-09-02刘雪勇王明红
刘雪勇, 王明红
(上海工程技术大学 机械与汽车工程学院, 上海 201620)
随着航空、航天、汽车、化工等工业的快速发展,高强度钢因具有高强度(RM>1 200 MPa)和高硬度(30~50 HRC)以及良好的综合力学性能而得到了广泛的应用[1]。但是高强度钢在加工过程中存在单位切削力大、局部切削温度高、断屑不畅等问题使得高强度钢的加工效率较低、加工成本较高[2-3]。关于如何提高高强度钢的制孔质量和加工效率,降低加工成本,国内外学者作了很多研究。
刀具优化方面:陈连银[4]通过将钻头刃带由1条增加为2条,设计出一种加工高强度钢用的四棱钻头,结果表明四棱钻头的切削更加平稳、零件孔壁的光洁度更高、钻头寿命更长;Pang Siqin等[5]在吸收普通群钻钻型经验的基础上,改变内外刃结构形式和参数,设计出一种用于钻削高强度钢的整体硬质合金群钻钻型,通过研究发现优化后的钻削力降低10%~20%,钻削效率(单位时间钻孔数)提高2~3倍,加工精度和表面质量提高约1级,钻削性能优良;于凤云等[6]针对钻削高强度钢EH360的刀具材料进行了优选分析,研究发现在加工高强度钢 EH360时,首选的刀具材料为W6Mo5Cr4V2Al,其次是YG8,再次是W18Cr4V;付雷杰等[7]针对钻削高强度钢20CrNiMo所用麻花钻的几何参数进行了研究,结果表明当螺旋角取20°,横刃斜角取53°,顶角取138°时,可以获得较好的钻削效果。
制孔工艺优化方面:马未未[8]利用遗传算法对高强度钢AISI4340的钻削用量进行了优化研究,优化结果表明当切削速度在40 m/min左右,进给量控制在0.08~0.114 mm/r时,钻削效果较为理想;付鑫[9]对钻削高强度钢34CrNi3MoV的断屑机理及振动特性进行了研究,提高了加工效率,改进了加工工艺;金成哲等[10]研究了钻削34CrNi3MoV高强度钢时切屑形态的变化规律,研究结果表明通过改变刀具几何参数和切削用量可以有效地改变切屑形态及切屑几何参数;金成哲等[11]还对钻削高强度钢34CrNi3MoV的切削振动特性进行了研究,为提高钻削加工效率、改进钻削高强度钢工艺提供了理论基础;李明等[12]通过有限元方法对高强度钢AISI4340高速直角切削进行了仿真,研究了切削速度、背吃刀量和刀具前角等切削参数对断屑的形成频率、平均单位切削力以及切削力的频率的影响;徐少红[13]研究了高强度钢与超高强度钢加工时的一些特性,为后续切削用量的优化做参考依据;龙震海等[14]在一定切削用量范围内设计3因素5水平试验,采用相关统计方法,对高强度钢高速铣削是切削力受切削参数的影响进行分析,建立切削力模型并进行残差分析验证设置的切削用量范围可被有效利用。
其他方面:王笑等[15]利用DEFORM-3D软件对42CrMo钢的车削过程进行了研究,分析了车削过程中切削力和切削温度的变化规律;岳彩旭等[16]对高强度磨具钢Cr12MoV切削过程中一些微观形貌,如变质层表面显微硬度、白层厚度等进行研究,分析了切削参数、刀具磨损等因素对已加工表面变质层的这些微观形貌变化的影响,对切削参数优化有一定参考价值;A.Jayaganth等[17]通过不同的加工工艺在SS410上进行了钻孔实验,分析了钻孔参数和加工环境对表面粗糙度和加工时间的影响;Jiménez-Pea.c等[18]使用不同的打孔技术,对由S500MC制成的中厚板进行了一系列疲劳测试,通过光学评估,硬度测试和粗糙度评估研究了每个孔加工过程的表面、几何形状和残余损伤,研究的结果可以估算出每种制孔工艺对特定高强度钢的适用性。
阶梯钻是一种在普通麻花钻基础上演变的钻扩一体式新型钻头,其结构设计思想来源于拉刀。阶梯钻的第1阶梯与普通麻花钻一致,以较小直径进行预孔加工,一定程度上减小了横刃对轴向力的影响程度;第2阶梯的设计则采用相对较大的后角,以获取较为锋利的第2切削刃,同时改善钻削过程中的散热条件;此外,由于第2阶梯的切削刃非常锋利,可以很好地去除第1阶梯在钻削过程中产生的毛刺,从而在一定程度上也有助于提高孔加工的质量。
为了解决高强度钢AISI4340钻削过程中存在轴向力大、钻削温度高、刀具磨损严重等问题,课题组采用自主设计的阶梯钻对高强度钢AISI4340进行钻削仿真研究,分析了加工过程中的钻削轴向力和刀具温度,并与普通麻花钻进行对比。为了便于比较,阶梯钻和麻花钻的转速和进给量均取为相同,即n=2 500 r·min-1,f=0.1 mm·r-1。
1 DEFORM-3D钻削仿真模型建立
1.1 阶梯钻和工件模型的参数设定及网格划分
利用SolidWorks建立了麻花钻和阶梯钻的三维模型,将模型导入DEFORM-3D有限元仿真软件中,建立了麻花钻和阶梯钻的实体仿真模型,材料选择WC硬质合金,钻头设置为刚性类型。圆柱体工件的直径D为12 mm,高H为4 mm,材料选40CrNi2MoA(AISI4340)高强度钢,工件类型设置为塑性。仿真所用的麻花钻和阶梯钻的相关尺寸如表1所示。阶梯钻的几何参数示意图见图1。DEFORM划分网格采用的是自适应网格划分技术,这样的划分可以防止单元在仿真过程中发生过度畸变而失真。课题组所选用的钻头和工件网格划分类型均采用相对网格,钻头的最大和最小网格尺寸的比例设为4,钻头网格数量设置为15 000;工件的最大和最小网格尺寸的比例设为6,工件网格数量设置为20 000。

图1 阶梯钻的几何参数示意图Figure 1 Schematic diagram of geometric parameters of step drill

表1 阶梯钻钻头的相关尺寸Table 1 Relevant dimensions of step drill bits
1.2 材料相关属性及边界条件设置
课题组在选择本构模型时选取国际上常采用的Johnson-Cook 本构模型,见式(1)。工件材料的 Johnson-Cook 模型参数见表2[19]。Johnson-Cook材料本构模型为:

表2 AISI4340的Johnson-Cook模型参数Table 2 Johnson-Cook model parameters of AISI4340
(1)
在边界条件设置中,工件侧面在各方向上的速度设置为0,限制工件的运动。刀具沿着Z轴向工件进给,绕Z轴旋转。边界条件设置示意图见图2。
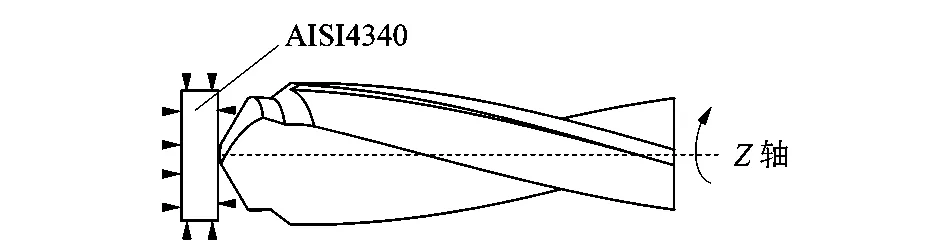
图2 边界条件设置示意图Figure 2 Schematic diagram of boundary condition setting
2 阶梯钻轴向力理论分析
由图3可知,阶梯钻头在稳定钻削工件过程中,钻削轴向力来源由3部分构成:横刃、第1主切削刃和第2主切削刃,其中钻头直径较小部分的轴向力由横刃和第1主切削刃共同构成。
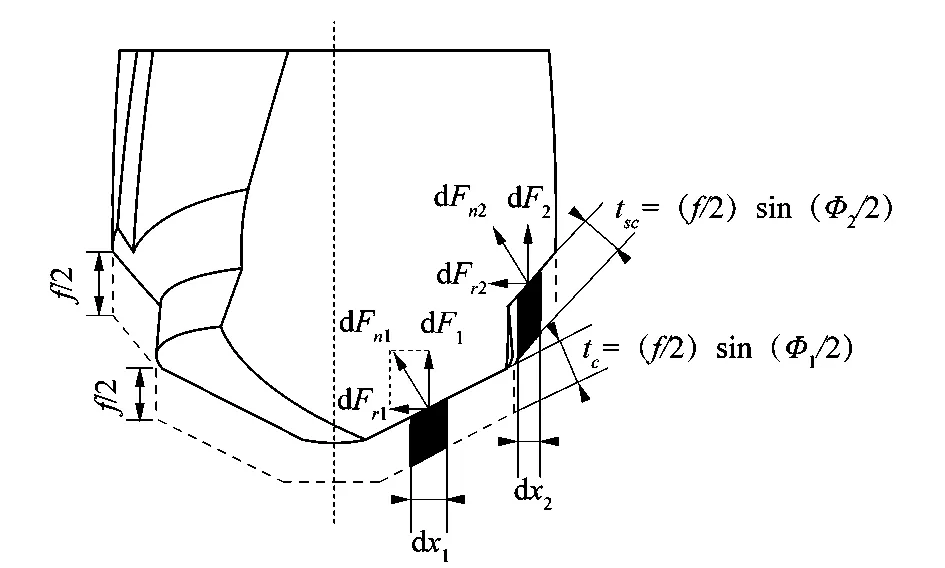
图3 阶梯钻主切削刃微单元切削力示意图Figure 3 Schematic diagram of micro-unit cutting force of main cutting edge of step drill
根据标准麻花钻轴向力计算公式,钻头直径较小部分的轴向力具体的计算过程如下:
FZ1=FC+2F1+2F2。
(2)
由经验得知,轴向力主要由横刃产生,因横刃是负前角工作,其轴向力很大,约占60%,主切削刃约占40%[20]。钻头主切削刃各点前角不同,为了方便计算,切削过程对主切削上各个离散的微元产生的轴向力简化为:
(3)
式中:Fn为微元处径向力Fr、切向力Fv和轴向力F1在微元处的合力;Φ1为阶梯钻的第1顶角,f为进给量,D1为第1阶梯的直径,ρ为主切削刃微单元整合的半径,τj和τu分别为ρ取值范围的上限和下限,Kn为轴向力修正系数。
(4)
(5)
式(5)中:V为切向速度;r为微元到钻心的半径;a,a0,a1,a2,a3和e均为第1阶梯轴向力的校正常数;γ为微元处的前角;ω为钻芯厚度的一半;tc为微元处的切削厚度;由于V均与ρ相关,C1为第1阶梯的轴向力综合修正常数,故做以上简单处理。
(6)
将式(5)、式(6)代入式(3)可得式(7)[21]:
(7)
F2除半径取值范围与F1不同外,其计算过程与F1一致,这里不再赘述。
同理,横刃部分的轴向力计算亦可采用上述的方法,但由于横刃部分不存在前角,故横刃部分的修正系数Knc略有不同:
(8)
式中:b,a4,a5和a6为横刃处轴向力的校正常数;C2为横刃处的轴向力综合修正常数。
由理论分析得到的公式可知,阶梯钻第2顶角小于第1顶角,使得阶梯钻第2主切削刃的轴向力小于同等条件下麻花钻的轴向力积分,故同等条件下阶梯钻产生的轴向力之和小于麻花钻。实际应用中,阶梯钻通常具有较大的螺旋角,也使得第2主切削刃更加锋利,产生的轴向力会更小。
3 仿真结果与分析
3.1 轴向力分析
在钻削高强度钢AISI4340的过程中,轴向力的大小直接影响着刀具磨损和制孔质量,对轴向力的研究有助于指导实际生产。由图4可知,在n=2 500 r·min-1,f=0.1 mm·r-1,Φ=118°时,麻花钻和阶梯钻的轴向力变化趋势相似,这里的顶角Φ对于阶梯钻而言指的是第1顶角,即Φ1。随着钻削深度增加,钻头每转一圈切除的材料体积增加,切削刃需要克服的阻力也随之增大,钻削轴向力明显增大,但随着钻削深度继续增加,钻削温度会相应升高,高强度钢会发生软化,材料硬度降低,导致轴向力有所降低,故轴向力呈现先增大后减小的变化趋势。由图4亦可知,钻削过程中,阶梯钻的轴向力要略低于麻花钻,这是由于阶梯钻第1阶梯直径小于麻花钻,使得单位时间内切削体积小于麻花钻,且随着第2阶梯参与切削,阶梯钻的排屑空间较普通麻花钻大,加之切削热量持续积累,以致于阶梯钻的轴向力降低幅度比麻花钻更明显。由具体的数值可知,钻削前期,即图4中仿真步数自1 000至5 000之间,麻花钻的轴向力均值为741.73 N,阶梯钻的轴向力均值为681.48 N,阶梯钻的轴向力比麻花钻小60.25 N;在第2阶梯参与切削期间,即图4中仿真步数自12 000至15 000之间,阶梯钻的轴向力均值为195.27 N,麻花钻在相同阶段的轴向力均值为331.08 N,阶梯钻的轴向力比麻花钻小135.81 N,这说明在钻削高强度钢AISI4340的过程中,阶梯钻比麻花钻更有优势。
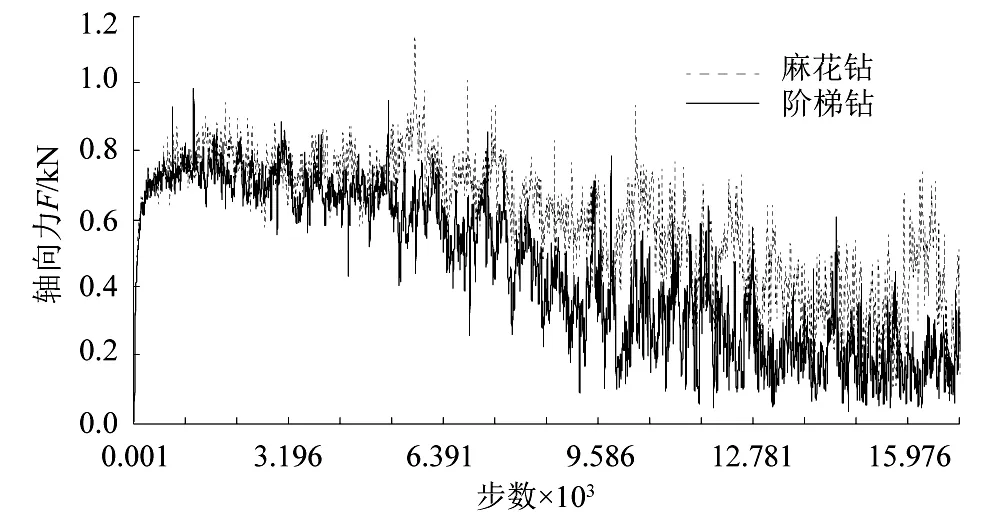
图4 2种钻头轴向力随步数变化曲线 (n=2 500 r·min-1,f=0.1 mm·r-1,Φ=118°)Figure 4 Changing curves of axial force of two kinds of drill bits with number of steps (n=2 500 r·min-1,f=0.1 mm·r-1,Φ=118°)
此外,课题组还对主轴转速、进给量和钻头顶角(阶梯钻仅指第1顶角)等因素对轴向力的影响规律进行了研究。由图5可知,在进给量和钻头顶角保持不变的条件下,随着主轴转速的增加, 2种钻头钻削过程中产生的轴向力均呈现减小的趋势,且麻花钻的轴向力极差值为104.93 N,同等条件下阶梯钻的轴向力极差值仅为15.98 N,即同等条件下,麻花钻产生的轴向力大小受主轴转速的影响较阶梯钻更大。
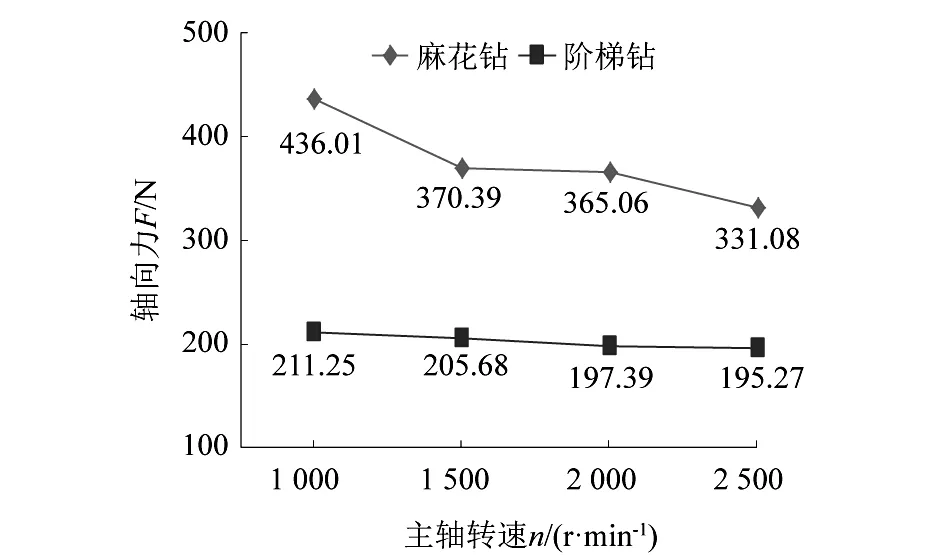
图5 2种钻头轴向力随主轴转速变化曲线 (f=0.1 mm·r-1,Φ=118°)Figure 5 Changing curves of axial force of two kinds of drill bits with spindle speed (f=0.1 mm·r-1,Φ=118°)
由图6可知,在主轴转速和钻头顶角保持不变的条件下,随着进给量的增加,2种钻头钻削过程中产生的轴向力均呈现增大的趋势。由图6亦可知,麻花钻的轴向力极差值为536.05 N,在相同条件下阶梯钻的轴向力极差值仅为50.36 N,即同等条件下,麻花钻产生的轴向力大小受进给量的影响较阶梯钻更大。
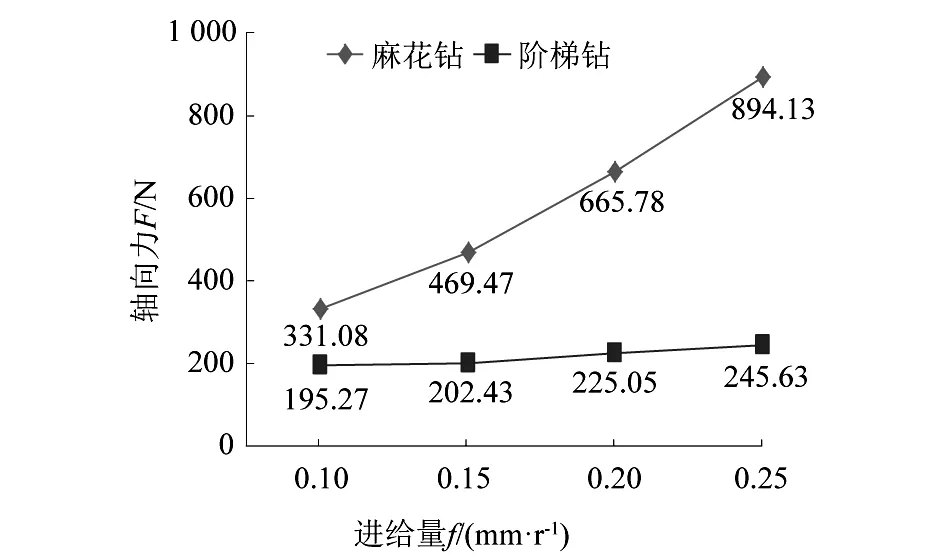
图6 2种钻头轴向力随进给量变化曲线 (n=2 500 r·min-1,Φ=118°)Figure 6 Changing curves of axial force of two kinds of drill bits with feed rate (n=2 500 r·min-1,Φ=118°)
由图7可知,在主轴转速和进给量保持不变的条件下,随着钻头顶角的增加,2种钻头钻削过程中产生的轴向力均呈现增大的趋势。这是由于顶角越小,则主切削刃越长,单位切削刃上的负荷相应地减轻,轴向力减小。由图7亦可知,麻花钻的轴向力极差值为320.60 N,在相同条件下阶梯钻的轴向力极差值仅为252.26 N,即同等条件下,麻花钻产生的轴向力大小受进给量的影响较阶梯钻更大。
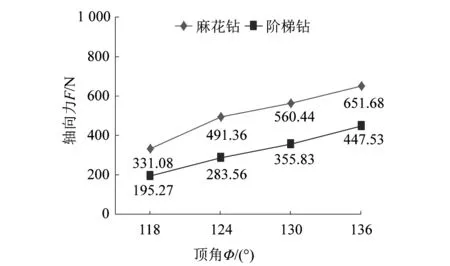
图7 2种钻头轴向力随顶角变化曲线 (n=2 500 r·min-1,f=0.1 mm·r-1)Figure 7 Changing curves of axial force of two kinds of drill bits with point angle (n=2 500 r·min-1,f=0.1 mm·r-1)
3.2 钻削温度分析
金属切削温度研究内容包含切削区的平均温度、刀具上的最高温度与温度分布、切屑上的最高温度与温度分布、工件上的最高温度与温度分布等。课题组主要研究工件和钻头上的最高温度与温度分布。
由图8可知,随着钻削深度h的增加,工件温度分布基本相似,由于阶梯钻的第1阶梯直径较小,钻削温度较为集中,通过工件传递的热量比麻花钻的多,导致阶梯钻钻削的工件温度扩散范围较大。由于阶梯钻的结构设置使得切屑更易排出,且排出的切屑温度也比麻花钻的高,切屑带走了一部分热量,所以阶梯钻钻削的工件最高温度低于麻花钻,证明阶梯钻散热条件比麻花钻好。
由图8还可以看出,钻削过程中,阶梯钻钻头最高温度大于麻花钻的钻头最高温度,这是由于阶梯钻的第1阶梯直径较小,使得钻削过程中横刃挤压工件产生的热量更加集中。虽然阶梯钻的最高温度比麻花钻的大,但温度分布更均匀,而麻花钻的钻头温度主要集中在主切削刃上,使得麻花钻更容易发生磨损,影响刀具寿命。

图8 2种钻头钻削过程中的温度分布 (n=2 500 r·min-1,f=0.1 mm·r-1,Φ=118°)Figure 8 Temperature distribution of two kinds of drill bits during drilling (n=2 500 r·min-1,f=0.1 mm·r-1,Φ=118°)
课题组还就主轴转速、进给量和钻头顶角(阶梯钻仅指第1顶角)等因素对钻削过程中钻头温度的影响进行了研究。由图9~图11可知,在保持2个试验因素不变的条件下,2种钻头的温度变化趋势一致,且阶梯钻的钻头温度均高于麻花钻。同等条件下,麻花钻钻头温度大小受主轴转速和进给量的影响较阶梯钻更大,但2种钻头温度受顶角影响差异不大。
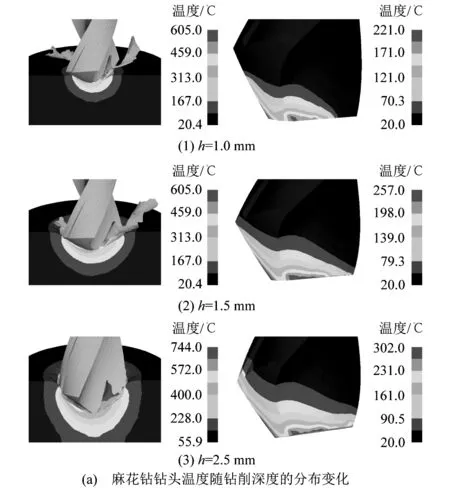
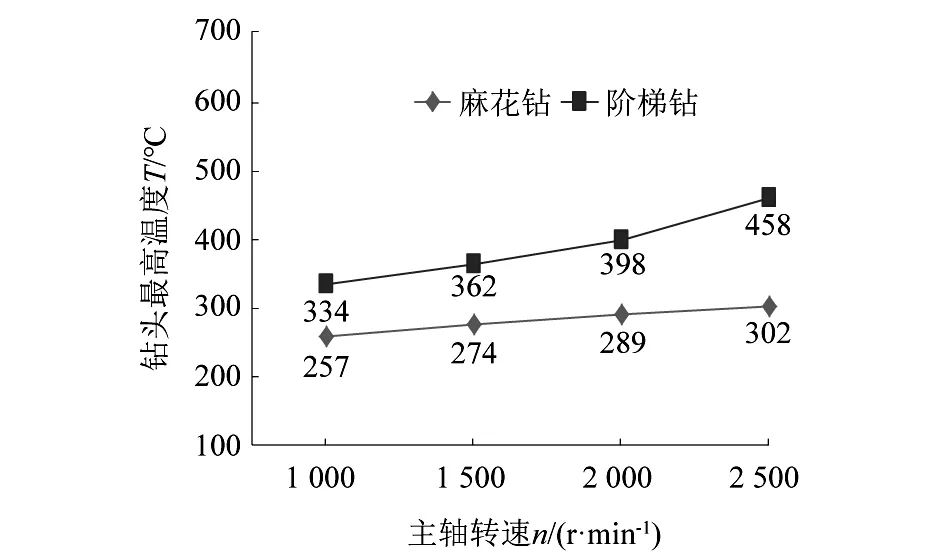
图9 2种钻头最高温度随主轴转速变化曲线 (f=0.1 mm·r-1,Φ=118°)Figure 9 Changing curves of maximum temperature of two drill bits with spindle speed (f=0.1 mm·r-1,Φ=118°)

图10 2种钻头最高温度随进给量变化曲线 (n=2 500 r·min-1,Φ=118°)Figure 10 Curves of maximum temperature of two kinds of drill bits varies with feed rate (n=2 500 r·min-1,Φ=118°)
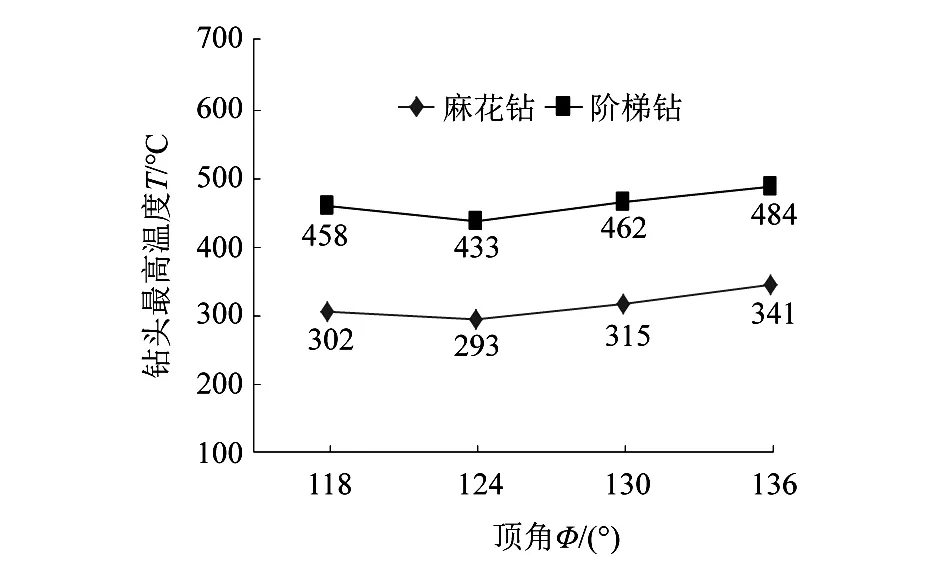
图11 2种钻头最高温度随顶角变化曲线 (n=2 500 r·min-1,f=0.1 mm·r-1)Figure 11 Curves of maximum temperature of two drill bits with point angle (n=2 500 r·min-1,f=0.1 mm·r-1)
由表3可知,对阶梯钻而言,对轴向力影响最大的是主轴转速,其次是进给量,最后是顶角。对麻花钻而言,对轴向力影响最大的是进给量,其次是主轴转速,最后是顶角。通过横向对比可知,麻花钻的钻头温度受进给量和顶角的影响较阶梯钻更大。结合前文研究发现:就钻头最高温度而言,钻头的标准顶角并不是最适合钻削高强度钢AISI4340的最佳值,最佳值在124°附近。
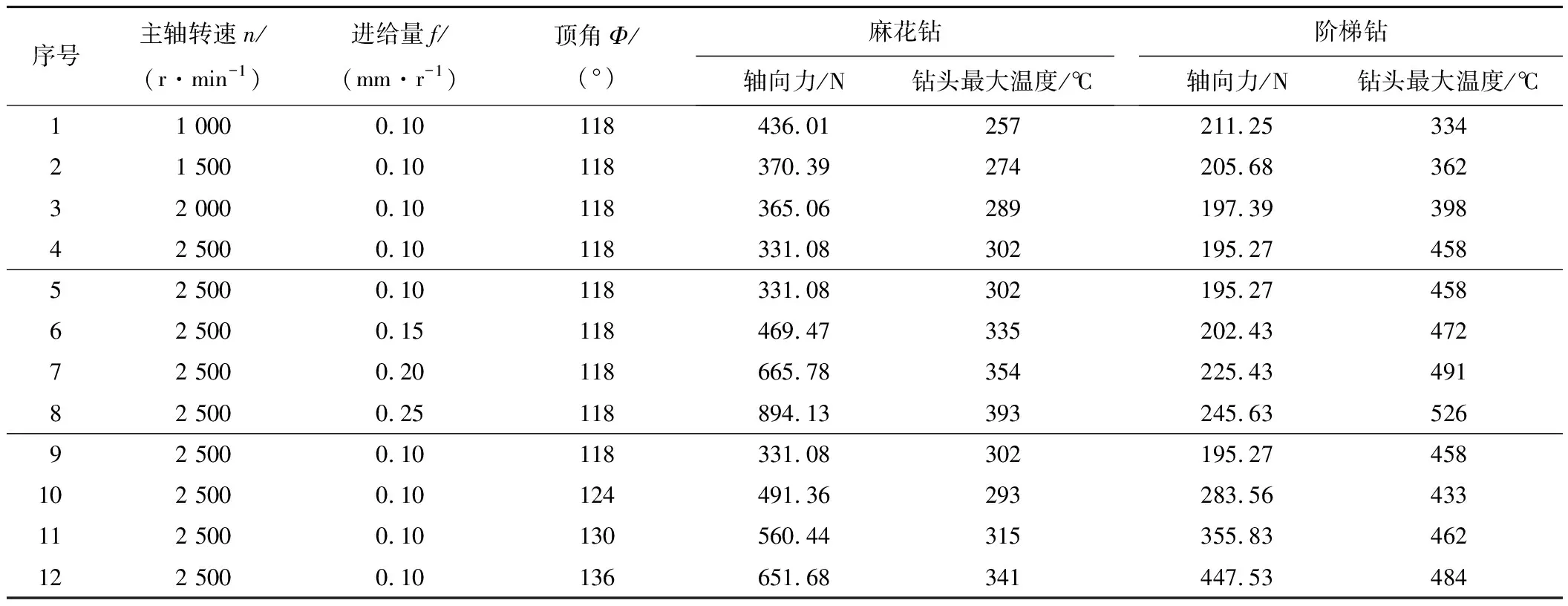
表3 各影响因素对2种钻头轴向力和钻头温度的影响对比Table 3 Comparison of influence of various influencing factors on axial force and temperature of two drill bits
4 结论
课题组利用有限元软件DEFORM-3D对高强度钢AISI4340的普通钻削和阶梯钻钻削过程进行模拟,对比分析了2种钻头钻削过程中轴向力和钻头最高温度,通过分析仿真结果得出以下结论:
1) 2种钻头在钻削过程中主轴转速、进给量和顶角等3个因素对轴向力和钻头温度的影响规律保持一致。
2) 对2种钻头而言,主轴转速对轴向力的影响最小,顶角对钻头最高温度的影响最小,且当阶梯钻n=2 500 r·min-1,f=0.1 mm·r-1,Φ=118°时轴向力最小。
3) 阶梯钻在降低轴向力方面比麻花钻更有优势,但钻头最高温度要高于麻花钻。就钻头最高温度而言,钻头的标准顶角并不是最适合钻削高强度钢AISI4340的最佳值,最佳值在124°附近。同时,钻头温度分布较麻花钻而言更加均匀,在延长刀具使用寿命方面更有优势。
