非MDS码存储系统的通用可靠性模型
2021-09-02聂世强郑旭达刘钊华伍卫国董小社张兴军
聂世强,郑旭达,刘钊华,伍卫国,董小社,张兴军
(西安交通大学 计算机科学与技术学院,陕西 西安 710049)
容错机制在大规模分布式存储系统中是不可或缺的。大规模存储系统由成千上万台服务器组成,诸多研究报告指出节点失效成为常态[1-3]。近年来,谷歌等大型数据中心的统计数据表明,平均每天都会有1%~2%的节点失效[1]。服务器失效引起数据丢失造成的损失是无法估量的。目前存储系统常用的数据冗余方法有多副本、纠删码等。多副本是将数据复制多份分别存放在不同的存储节点,只要数据的副本所在节点不同时失效,数据便不会丢失[4],纠删码是将数据分割为相等的数据块,采用编码策略生成校验块,部分数据块丢失后,可以通过编码恢复[5]。不同于多副本对存储空间的大量需求,纠删码可以显著降低存储开销,因此被广泛使用,如云存储系统:Giza[6]、Hybris[7]等。然而目前纠删码在可靠性、存储利用率等方面都不同程度地存在缺陷,难以同时达到理想的状态[8-9]。
可靠性可以判断系统或设备是否具备持续有效提供正确数据服务的能力,因此在存储系统中,可靠性是与性能和费用等指标重要性相当的一个评价标准。为了探究存储系统可靠性与诸多因素的关系,很多学者都对存储系统可靠性展开了广泛的研究。早期如PATTERSON采用马尔可夫模型分析磁盘矩阵系统可靠性,并以平均数据丢失时间 (Mean Time To Data Loss,MTTDL) 作为可靠性评价指标[10]。当前研究的方向有考虑数据放置算法[11]、数据中心物理拓扑结构[12]等因素对系统可靠性的影响。穆飞等针对大规模副本存储系统建立了马尔可夫模型,度量了系统规模、副本阶数、节点容量等对可靠性的影响[13]。HUANG等提出了在Windows Azure存储系统使用局部修复码(Locally Repairable Codes,LRC)以降低数据修复过程中的网络传输数据量,并建立了马尔可夫模型,对局部修复码与里德-所罗门码(Reed-Solomon codes,RS)进行可靠性的比较[14]。同时也有大量对于纠删码的研究[15-17]。HU等人根据存储介质的可靠性提出变长的UFP-LRC码[18],并对其可靠性进行数值分析。郝晓慧等也对局部修复码的构造进行了研究[19]。HAFNER等对低密度奇偶校验码( Low-Density Parity-Check,LDPC)和WEAVER码两种非最大距离可分码(Maximum Distance Separable code,MDS)建立了可靠性模型,但是并未针对所有非最大距离可分码进行研究,该方法不具通用性[20]。
综上所述,当前对存储系统可靠性研究涉及了诸多方面,对特定的非最大距离可分码与存储系统可靠性分析也有相关研究。然而对非最大距离可分码的数据失效若干块后,剩余块的可修复概率求解仍是尚未解决的问题,并且针对采用非最大距离可分码的存储系统也缺乏较为通用的可靠性模型。因此,笔者对采用非最大距离可分码的存储系统可靠性进行了研究。与现有研究基于特定校验码以抽样概率计算方法不同,从非最大距离可分码的构造矩阵入手,提出一种求解非最大距离可分码丢失若干块后的可修复概率计算方法,并提出了一种采用面向非最大距离可分码存储系统的通用可靠性模型,最后数值分析以局部修复码为例验证了模型的正确性,并且比较了不同因素对存储系统可靠性的影响。
1 存储系统可靠性模型
1.1 背景知识
分布式存储系统由多个对象存储设备 (Object-based Storage Device,OSD)组成。存储系统对外提供的数据读写单元以对象为粒度,客户端的对象X会在存储系统内部分割为d个数据块,并且按照不同的纠删码规则生成p个校验块;对象X的数据块和校验块被随机分布到所有的存储节点中,同一对象的数据块和校验块不会在相同存储节点存储。
若采用多副本或最大距离可分码存储系统建模非最大距离可分码存储系统可靠性,其结果是不准确的。因为多副本和纠删码中的最大距离可分码的容错能力是确定的,而非最大距离可分码的容错能力是具有一定概率的,以(6,2,2)局部修复码为例说明,对象X被分割为6个数据块x0,x1,x2,x3,x4,x5,并生成局部效验块px,py和全局校验块p0,p1,由于局部修复码是非最大距离可分码,它是无法容忍任意4个块失效的,如图1所示。

(a) 失效x0、x1、x3和x4节点

(b) 失效x0、x1、x2和px节点
图1(a)和(b)所示分别表示(6,2,2)局部修复码失效4个块的2种不同情况,对于图(a)来说,失效x0,x1,x3和x4节点,可以使用px,py和p0,p14个校验块修复对象X;对于图(b)来说,失效x0,x1,x2和px节点以后,校验块py对于修复过程无任何意义,校验块p0和p1只能修复2个数据块,因此对象X无法恢复,对于(6,2,2)局部修复码中丢失任意4个块,对象X只有87%的概率可以恢复[14]。
算法1非MDS码可恢复概率求解算法。
输入:
M:非MDS的m×n生成子矩阵。
lost:丢失的块数(任意的数据块和校验块)。
输出:
P:可恢复概率值。
过程:
recovery=0;∥可恢复组合数
total=0;∥所有丢失块的可能组合数
block=[i for i in range(m)];
for(i=0;i++;i≤lost) ∥i表示丢失的校验块数
all_combin+=combinations(m,i)]
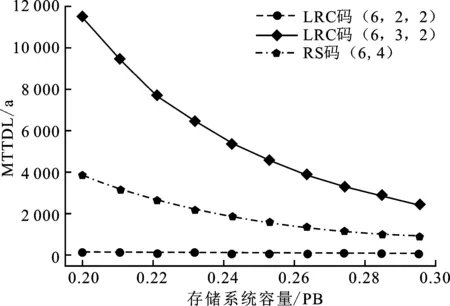
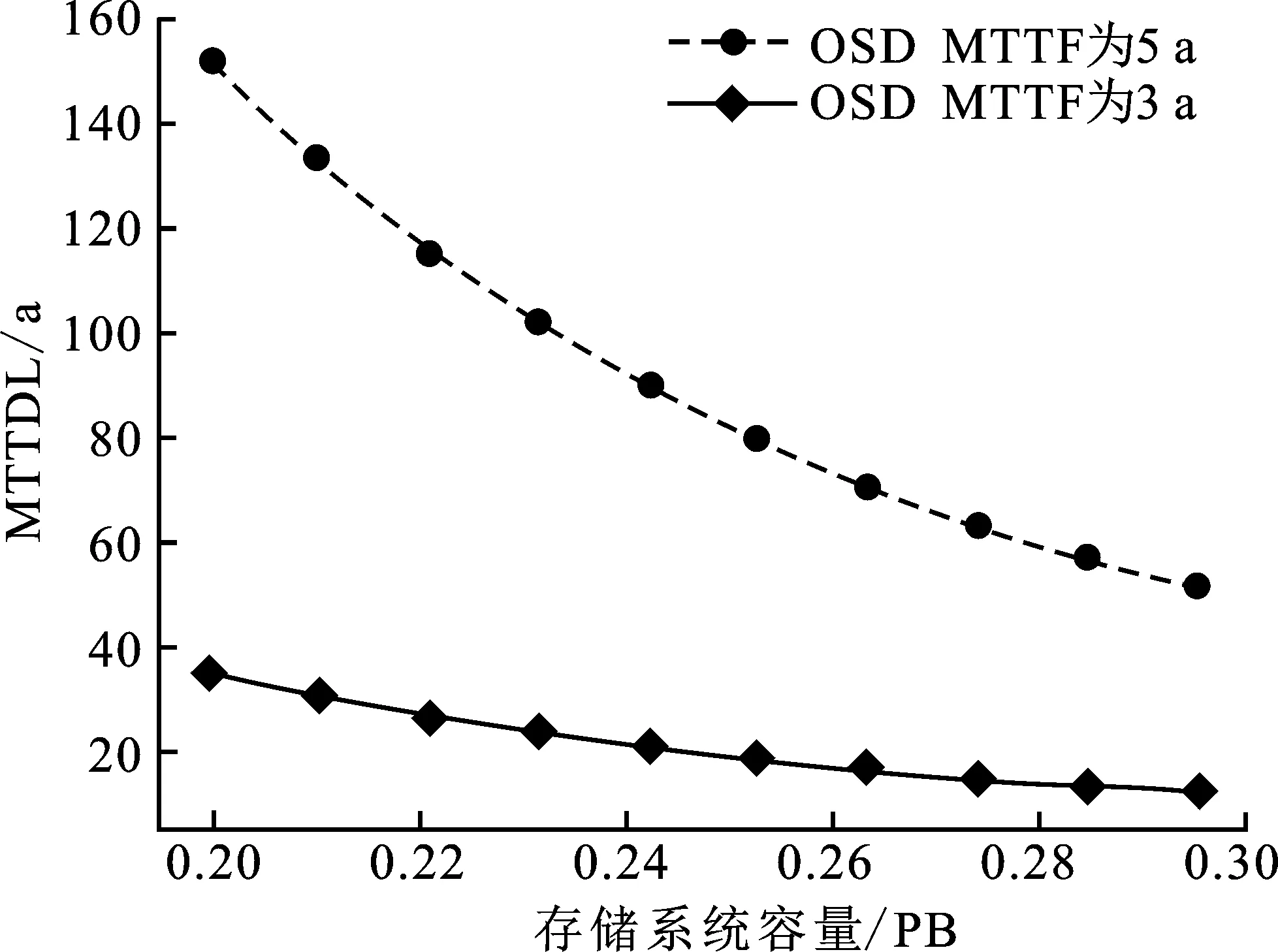
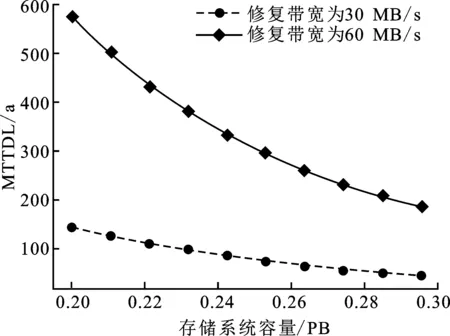
while(i ∥遍历丢失的校验块数 parity=length(all_combin[i]) if(lost-parity = =0):∥未丢失数据块 recovery+=1; total+=1; else: ∥丢失数据块的所有组合 data += combinations(lost - parity); for(j=0;j matrix_A=M [all_combin[i]^block,:]; matrix_B= matrix_A[:,data[j]]; row,column=matrix_B。shape; if( row =column): recovery+=1 if det(matrix_B)= =1 else 0 else( row>column): for sub_matrix in matrix_B: if det(sub_matrix)= =1: recovery+=1; break; total+=1; p=recovery/total; return P;∥遍历求解可恢复的概率值。 针对最大距离可分码和多副本存储系统的可靠性模型,大都基于马尔可夫理论,通常只考虑数据丢失的情况,不考虑其他诸如内核升级、临时性停电导致的数据临时性无法访问,模型中仅考虑硬盘的失效和修复。笔者所建立的模型也遵循此前提。 为了建立针对采用非最大距离可分码的存储系统的较为通用的可靠性理论模型,笔者提出了一种基于矩阵运算的求解任意非最大距离可分码失效若干块后可恢复概率求解算法。这里非最大距离可分码指的是不满足Singleton边界条件的编码方式的纠删码,如局部修复码、低密度奇偶校验码和WEAVER码等。纠删码的不同之处在于编码和译码过程,编码过程中将对象分割成多个数据块,不同的纠删码生成特定的生成矩阵,对数据块和生成矩阵进行矩阵运算生成校验块,在可容忍的范围内丢失若干块后,剩余的块和生成矩阵逆运算能恢复出丢失的块。 表1 模型中包含的变量和含义 使用MTTDL平均数据丢失时间作为非最大距离可分码存储系统的可靠性评价指标。首先定义了如表1中的变量和其含义,特别指出的是表1中k的含义是指非最大距离可分码中失效任意k块都能恢复的最大值。 非最大距离可分码存储系统马尔可夫模型如图2所示。 图2 非最大距离可分码存储系统可靠性模型 首先计算非最大距离可分码存储系统状态转移图中的各个状态间的转换速率,即状态Si到状态Si+1的失效速率,状态Si到状态Si-1的修复速率,状态Si到Sstop吸收态的速率。 状态Si到状态Si+1的失效速率计算需要分为2个阶段。第1个阶段是失效k个对象存储设备节点以内的情况,包括状态S0到状态Sk的阶段。因为对象的数据块和校验块是随机分布到所有对象存储设备节点的,则失效节点数目小于k的情况下系统失效任何节点数目都不会造成数据丢失,状态Si转换到状态Si+1的失效速率为r(n-i)。第2阶段是失效节点数目大于k的情况,在状态Sk到状态Sp的阶段,若失效i个节点后其下一个状态则可能是Sstop状态或Si+1状态。 (1) 若状态Si的下一状态是Si+1,不发生数据丢失情况的失效速率: (1) (2) 若状态Si的下一状态是Sstop,则发生数据丢失情况的概率: (2) 对象存储系统平均每个存储节点的存储数据量为C/n,节点失效后数据的平均修复时间为C/nb,则状态Si到状态Si-1的修复速率为inb/C。 通过以上分析能够得到非最大距离可分存储系统马尔可夫模型的状态转移矩阵Q,状态转移矩阵Q的元素表达式如下: (3) 非局部修复码存储系统可靠性影响因素众多,笔者利用建立的可靠性模型量化不同因素对可靠性的影响。非局部修复存储系统可靠性数值计算程序采用python语言实现。设单个硬盘容量为2 TB,数据修复带宽只占系统总带宽的一部分,假设系统分给对象存储设备节点恢复的带宽为30 MB/s,单存储节点的平均失效时间为5年。首先比较了在相同配置下常见的RS码(最大距离可分码)和局部修复码(非最大距离可分码)对可靠性的影响。如图3所示,比较(6,4)RS码、(6,2,2)局部修复码和(6,3,2)局部修复码的可靠性,从图中可以看出,在相同系统容量下(6,3,2)局部修复码的可靠性最高,(6,4)RS码次之,(6,2,2)局部修复码最低。在系统容量较低时,采用不同配置的纠删码存储系统MTTDL较为明显,呈现数倍的差异;随着存储系统容量的增大,不同配置的纠删码存储系统可靠性都随之下降。(6,3,2)局部修复码最低可容忍3个块丢失,最高可容忍5个块丢失,而(6,4)RS码仅能容忍4个块丢失,(6,2,2)局部修复码最高可以容忍4个块丢失。实验仿真结果与理论分析较为一致,可以一定程度说明模型是符合真实情况的。 随后量化对象存储设备节点的可靠性对系统的影响。实验计算分析针对PB级存储系统,固定其他参数不变,仅改变硬盘的MTTDL,比较系统MTTDL变化趋势,计算结果如图4所示。可以发现,系统的平均数据丢失时间随着存储系统规模的增加而不断降低,虽然采用了纠删码容错,系统可以容忍一定数量的硬盘失效而不造成数据丢失,但是在相同存储规模下,硬盘失效时间为5年的系统的可靠性更大。主要是因为当对象存储设备节点的可靠性较低时,很可能出现某些硬盘失效后系统进行修复过程中又出现其他硬盘失效,频繁失效造成的数据恢复需求超出系统的修复能力,因此系统的可靠性将会大大降低。 图3 纠删码配置与存储系统可靠性的关系 图4 硬盘寿命与存储系统可靠性的关系 存储系统的网络带宽不仅仅影响系统的性能,也影响了节点失效后系统的修复过程,如图5 所示。比较不同的修复带宽对可靠性的影响,可以看出,修复带宽为60 MB/s时系统的可靠性比修复带宽为30 MB/s时更高,并且随着存储规模的增大而降低。主要是因为系统存储节点失效后其修复时间受失效对象存储设备节点数目、对象存储设备节点容量和修复带宽的影响,修复带宽越大,修复的时间越短,在修复时间内其他存储节点发生失效的概率越低,因此数据丢失的概率越低,存储系统更加可靠。 图5 带宽与存储系统可靠性的关系 图6 硬盘容量与存储系统可靠性的关系 最后考察存储系统可靠性与存储节点容量的关系,如图6所示。在相同存储规模下,存储节点容量越大,可靠性越高。因为系统存储节点失效后其修复时间与节点容量成正比,容量越大,修复时间越长;而存储容量越大,在相同存储规模的条件下,其存储节点数目也会相应减少。因此可以得出在相同存储规模的条件下,存储节点数目对可靠性的影响比存储节点容量对可靠性的影响更大。随后在存储设备节点数目相等的条件下,对具有不同存储节点容量的存储系统进行比较,图中存储节点容量为1 TB时其存储规模为0.2 PB,相对于的是存储节点容量2 TB时存储规模为0.4 TB。从图中单硬盘容量2 TB的可靠性趋势变化中可以看出,在存储节点数相等的前提下,单硬盘容量2 TB组成的存储系统比单硬盘容量1 TB组成的存储系统可靠性更低。这也是与实际相契合的。 由于对大规模存储系统的可靠性实测需要消耗数年的时间,开销巨大,因此建立度量分布式存储系统可靠性理论模型显得尤为重要。面向大规模存储系统,首先提出了通用的非最大距离可分码失效若干块后可恢复概率求解算法。随后建立了可度量非最大距离可分码存储系统可靠性的理论模型。最后通过数值分析以局部修复码为例验证了模型的正确性,比较分析了存储系统中不同纠删码配置参数、节点容量和节点失效时间、修复带宽对系统可靠性的影响,为搭建真实的存储系统提供了相应的参考,具有一定的理论价值。1.2 非最大距离可分码可恢复概率求解算法

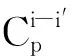
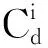
1.3 模型描述

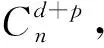


2 模型分析

3 总 结
