一种应用博弈和L0约束的盲图像修复方法

冯象初，王 萍，何瑞强

(西安电子科技大学 数学与统计学院，陕西 西安 710126)

图像在获取或处理的过程中，会受到采集设备或传输设备的影响，使得部分信息丢失或者毁坏[1-2]。为了解决这一类的退化问题，需要使用图像修复技术。目前图像修复主要应用于场景元素的去除、文物艺术品的保护、天文及遥感等领域[3-7]，具有重要的学术价值和应用价值。

图像修复[8-10]主要是利用某种规则或方法，根据图像中已知区域的信息来推断缺失区域内容并将其修复的技术。修复质量在很大程度上取决于对退化过程的掌握和原始图像先验信息的了解程度。大多数图像修复模型假定已知图像缺失区域，但在实际中，图像缺失区域也是未知的。由观测图出发，对缺失区域和原始图像同时进行估计，这类问题称为盲图像修复[11-13]。在修复的过程中，不仅要保持图像结构的连续性，而且要尽可能达到或接近原始图像的效果，同时尽量使得修复后的图像真实自然，修补的痕迹不易被观察者察觉，符合人们的视觉连贯性。

在无噪声环境下的图像退化[11-15]模型为

(1)

其中，f是原始图像u的退化图像，K是线性算子，Λ是图像中特定像素集标签，随机值v是被其他原因退化的像素值。图像修复的主要目标就是根据观测图像f估计出原始图像u。像素集标签Λc表示需要恢复的区域，在一般情况下假定是已知的。但在实际应用中，修复区域很难直接获得。盲修复就是在修复区域Λc和原始图像u都是未知的情况下，根据实际观测图像f的部分信息，对原始图像u进行估计的过程。图像修复是一个非适定的逆问题，为了解决该问题的非适定性，需要在最小化模型的基础上增加对原始图像u和修复区域Λc适当的正则项。

通过引入二值掩膜O(当i∈Λ时，O等于1；当i∈Λc时，O等于0)将退化模型进行转化，利用L0范数及其等价形式对数据项和修复区域进行稀疏性约束，对原始图像u采用TV[16](Total Variation)约束。根据修复区域的不同信息(已知或未知)，分别建立了非盲和盲图像修复模型；利用增广拉格朗日函数和博弈理论，建立了数值求解算法并进行仿真。

1 模型的建立

基于正则化的图像修复模型可表示为下面的最优化问题：

(2)

为了方便叙述，定义二值掩膜O(当像素属于Λ时，O等于1，否则等于0)，式(1)转化为

OΛf=OΛ(Ku+ε)=Ku+ε，OΛcf=OΛc(v)=0 。

(3)

假设图像像素值的动态范围为[umin，umax]，其中umin=0，umax=1，根据O建立不同的修复模型。

非盲图像修复模型(O已知)：由于L0范数在优化过程中能够保留图像边缘并具有较好的稀疏性，将L0范数应用到数据项，使得修复的结果图和原始图像之间的相似度较高，并且不易出现边缘模糊的现象。对原始图像u选用TV[16]进行约束，保证修复后的图像尽可能的光滑，则修复模型为

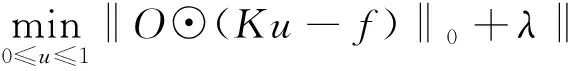
(4)

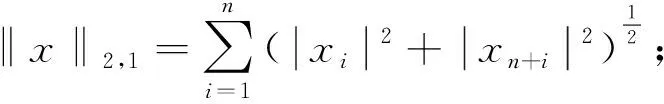
盲图像修复模型(O未知)：盲图像修复是在原始图像u和二值掩膜O都是未知的情况下，根据观测图像的部分信息进行修复。在修复的过程中不仅修复出原始图像，还需要估计出二值掩膜。因此，在模型式(4)的基础上增加L0范数对二值掩膜O的约束，以模拟丢失的像素是稀疏的，则盲修复模型为

(5)

其中，λ1和λ2是正参数，0<λ2<1。

式(4)和式(5)都选用了L0范数，为了便于求解，需要将其进一步转化。

2 模型(4)的转化与求解

2.1 模型(4)的转化

利用引理1[17](Mathematical Program with Equilibrium Constraints，MPEC)对L0范数进行替换。

引理1对于任给的向量w∈Rn，有以下结论成立：

(6)

其中，〈，〉表示内积；向量v中的元素vi∈[0，1]。v*=1-sign(|w|)，是式(6)最小化问题的惟一最优解。

根据引理1，引入辅助变量v，将非盲图像修复模型式(4)转化为：

(7)

如果u*是式(4)的全局最优解，则(u*，1-sign(|Ku*-f|))是式(7)的全局最优解；相反，如果(u*，v*)是式(7)的全局最优解，则u*是式(4)的全局最优解。虽然式(7)中的带平衡约束的数字规划(MPEC)问题是在式(4)的基础上增加L0范数的维度得到的，但它并没有产生额外的局部最优解。相比于式(4)，式(7)是一个非凸非光滑的最小值问题，它的非凸性是由于增加了v⊙|O⊙(Ku-f)|=0的约束而导致的。下面给出模型式(7)的求解方法。

2.2 PADMM算法

式(7)中的L0范数不显式存在，但由于它的非凸非光滑性，很难进行求解。笔者在proximal ADMM[18]算法的基础上，通过不断迭代地更新式(7)的增广拉格朗日函数中的原始变量和对偶变量得到最优解。

首先，引入两个辅助变量x，y，将式(7)转化为

(8)

式(8)是关于两个变量的优化问题，且目标函数是两块可分的凸问题。ADMM算法[19]能够利用目标函数的可分性，将其分解成几个子问题。

然后，并行求解每个子问题，提高算法的运行速度。主要解决可分解的凸优化问题，在弱条件下的收敛性仍成立。并在实际应用中，ADMM较原始的对偶方法(如对偶下降法，乘子法)收敛速度更快，则式(8)的增广拉格朗日函数为

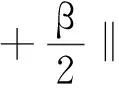
(9)

其中，ξ，ζ，π分别是∇u=x，Ku-f=y和v⊙O⊙|y|=0约束的增广拉格朗日乘子(对偶变量)；β>0，是惩罚参数。ADMM更新是通过固定其他原始变量和对偶变量，每次只优化一组变量，对偶变量采用梯度上升法进行更新的。在算法1中，为了方便叙述，将第t次迭代的增广拉格朗日函数记为Lt(·)。变量更新时，除了当前变量外，其他原始和对偶变量都保持当前估计值。

算法1具有可分结构的凸优化问题式(8)的proximal ADMM。其主要步骤为：

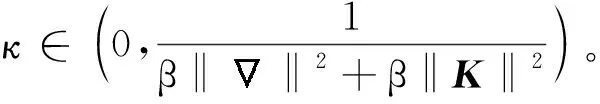
(10)

(11)

(12)

步骤3 更新增广拉格朗日乘子：

ξt+1=ξt+β(∇ut-xt) ，

(13)

ζt+1=ζt+β(Kut-f-yt) ，

(14)

πt+1=πt+β(vt⊙O⊙|yt|) 。

(15)

步骤4 迭代停止条件：如果t>30且‖∇ut-xt‖+‖Kut-f-yt‖+‖vt⊙O⊙|yt|‖<1/255。

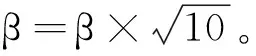
步骤6 令t=t+1，重复计算步骤1～步骤5。

步骤7 输出最优估计值u。

下面详细讨论式(10)～(12)的求解。

(16)

因此，式(10)的解为

ut+1=min(1，max(0，gt)) 。

(17)

ct=1-O⊙πt⊙|yt|，st=O⊙yt。

通过计算，式(11)的解为

(18)

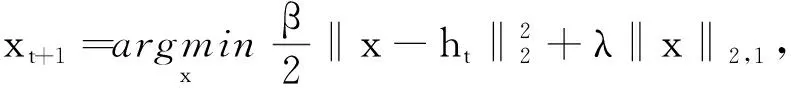
通过计算，变量x的解为

(19)

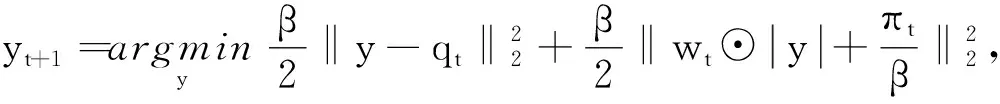
qt=Kut-f+ζt/β，wt=O⊙vt+1。

通过计算，变量y的解为

(20)

算法1在实践中有很好的收敛性，但式(7)是一个非凸的优化问题，因此必须加入额外的条件保证其收敛到KKT(Karush-Kuhn-Tucker)点。

下面给出算法1 的收敛性。

定理1算法1的收敛性[17]。

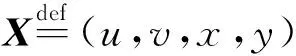
2.3 非盲图像修复模型的求解

非盲修复模型式(4)利用L0范数的等价形式，转化为式(7)，其目标函数是带有等式约束的两块可分的凸问题，可利用算法1求出最优解。

算法2非盲修复模型式(4)的求解。其主要步骤为：

步骤1 输入观测图像f；

步骤2 设置初始参数λ；

3 模型(5)的转化与求解

3.1 模型(5)的转化

盲图像修复模型式(5)：

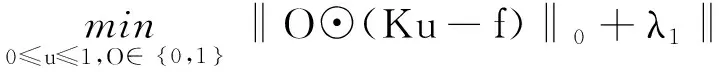
其中，λ1和λ2是正参数，0<λ2<1。

由于盲图像修复是关于原始图像u和二值掩膜O的最小化问题，是两个不同的目标，而博弈论是分析多个参与者之间决策相互影响的数学理论，其3个要素为参与者、决策集、目标函数，一个参与者在自己的决策集中确定的决策方案不仅影响到自己的目标函数值，也影响到其他参与者的决策选择。因此，假设参与者A修复原始图像，参与者B估计二值掩膜，A要在所有可能的图像中找到最优的恢复图像，B要在所有的可能中找到最优的缺失区域信息，在求解过程中，关键是双方目标函数的选择。A的目标函数为

(21)

式(21)的极小值对应恢复的结果图，O作为参数。B的目标函数为

(22)

式(22)的极小值对应缺失区域的信息，u作为参数。

式(21)意味着如果给定O，参与者A可以利用能量泛函恢复出干净图像u。对B来说，如果有干净图像u，则可以利用式(22)得到最优的缺失区域。二值博弈，达到纳什均衡点(u*，O*)。因此，利用博弈理论对u和O交替迭代。

由于式(21)中的数据项选用了L0范数，使其计算困难。与非盲问题类似，利用引理1，通过引入辅助变量v，将其进一步转化为

(23)

尽管式(22)中有两个L0范数，但其解可直接给出，所以保持其形式不变。最终的迭代公式为

3.2 盲图像修复模型的求解

盲修复要得到干净图像和缺失区域，这两个目标相互影响，符合博弈的性质。根据博弈论将盲修复模型式(5)分解成两个目标的交替迭代，在此过程中，干净图像的估计和非盲修复模型类似，用算法2求得，然后与缺失区域交替迭代。

算法3盲修复模型式(5)的基于博弈的两个变量的交替迭代方法。其主要步骤为：

步骤1 输入观测图像f。

步骤2 设置初始参数λ1和初始估计值O。

步骤3 交替求解子问题：① 给定Ot通过式(23)求解出ut+1；

② 将ut+1代入式(22)求解出Ot+1。

步骤4 迭代停止条件：max|ut+1-ut|<1e-4或max|Ot+1-Ot|=0。

步骤5 令t=t+1，重复计算步骤3～步骤4。

下面详细叙述式(23)和式(22)的求解。

①u子问题式(23)的求解：

在二值掩膜O给定的情况下，式(23)和非盲图像修复模型式(7)相似，可根据算法2求出最优的u。

②O子问题式(22)为

因为0<λ2<1，通过计算，式(22)的解为

(24)

如果有干净图像u，则可根据式(24)求出最优的O。

4 实验结果

4.1 实验环境

在Windows10下，使用8GB内存Inter(R)Core(TM)i5-8250U CPU @1.60Hz 1.80GHZ.PC及MATLAB2018软件。

4.2 模型测试

该部分主要对上面提出的修复模型进行测试。根据退化算子是单位算子(单位矩阵)或模糊算子(标准差为0.5，大小为3×3的高斯滤波)、二值掩膜的已知和未知及其不同比例(图像丢失像素的个数占整个图像像素个数的比例)4种情况进行测试，采用峰值信噪比(Peak Signal to Noise Ratios，PSNR)对修复图像进行客观评价。

用随机生成二值矩阵来模拟图像的缺失区域得到退化图像。在非盲修复中，图像缺失信息是已知的，修复的过程中用到了缺失区域的信息；在盲修复中，图像缺失区域的信息是未知的，修复时首先任给一个初始的缺失信息，然后通过干净图像和缺失区域的交替迭代得到最优解。不失一般性，为了对实验结果进行对比，采用“lenna”图进行仿真。图1和图2分别是退化算子为单位算子且像素值缺失40%以及模糊算子和像素值缺失20%的情况下，文中修复算法得到的实验结果。在主观条件下，算法2和算法3的恢复效果无明显差别。

图1 在单位算子的情况下，“lenna”图缺失40%的实验图像

图2 在模糊算子的情况下，“lenna”图缺失20%的实验图像

下面进行客观质量评价。当“lenna”图缺失不同比例时，两种算法恢复出结果图的峰值信噪比值如表1和表2所示。在客观条件下，当退化算子相同时，算法2比算法3恢复的效果好。当模型相同时，退化算子是模糊算子，相比较单位算子，恢复出原始图像的效果要好。

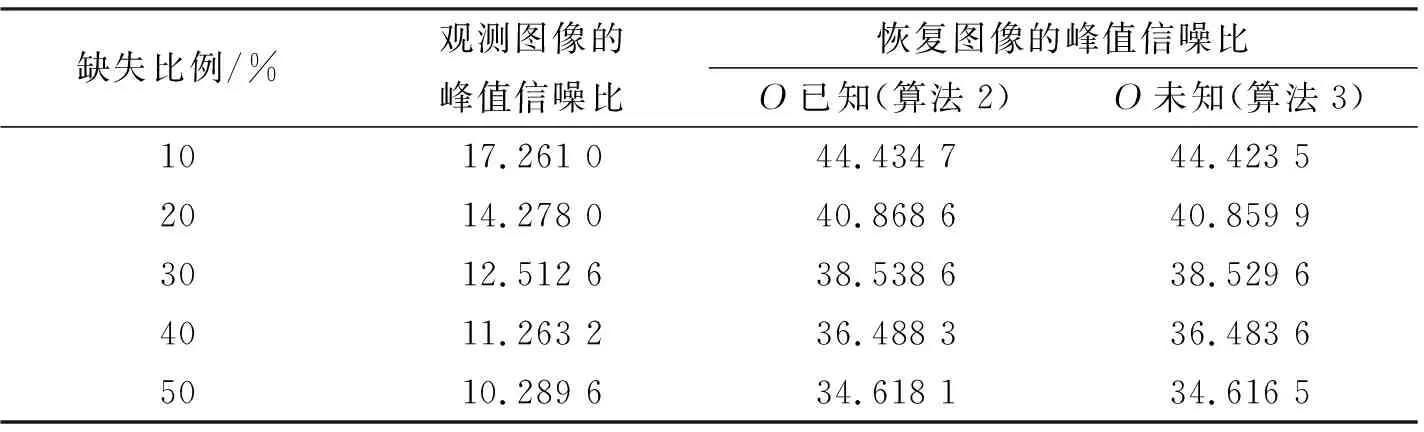
表1 退化算子是单位算子时的峰值信噪比

表2 退化算子是模糊算子时的峰值信噪比

4.3 收敛性分析

不失一般性，对“house”图像缺失30%且退化算子是模糊算子进行收敛性分析，记录每次迭代时的目标函数值，得到图3。

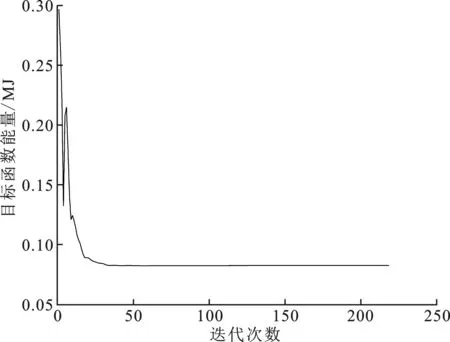
(a) 非盲修复能量变化

(b) 盲修复能量变化

在非盲修复能量变化图3(a)中，由于目标函数的非凸性和拉格朗日乘子的动态更新(算法1)，目标函数值不一定是单调下降的；在迭代20次之后目标函数值保持稳定，说明非盲修复模型(算法2)是收敛的。在盲修复能量变化图3(b)中，迭代次数较少，因为该模型是在非盲修复算法得到较好的结果的基础上进行的交替迭代，在迭代5次以后目标函数值基本不变，表明盲修复模型(算法3)是收敛的。

4.4 算法对比

下列的3种修复算法和文中算法类似，是用来解决基于正则化建立的修复模型。采用基于梯度的正则模型，主要区别是数据项或正则项的约束有所不同。① L02TV_AOP[20](The Adaptive Outlier Pursuit)：用L2范数作为数据项约束，L0范数对图像未知缺失区域进行稀疏性约束建立的盲修复模型，采用自适应异常点追踪算法求解。② L1TV_SBM[21](The Split Bregman Method)：选用L1范数对数据项约束并用分裂的Bregman方法进行求解。③ L0TV_PDA[22](The Penalty Decomposition Algorithm)：采用L0范数对数据项约束并用惩罚分解算法求解。故选择它们进行实验结果对比。

由于L02TV_AOP是对盲图像建立的修复模型，L1TV_SBM和L0TV_PDA是对非盲图像建立的修复模型，因此对L1TV_SBM和L0TV_PDA模型进行非盲图像测试，对L02TV_AOP模型进行盲图像修复测试。实验中，观测图像与文中算法测试的处理方法一致，不失一般性，选用“cameraman”图进行测试。表3和表4分别是当退化算子是单位算子和模糊算子的情况下的非盲图像修复的结果，表5和表6分别是当退化算子是单位算子和模糊算子的情况下的盲图像修复的结果。

表3 退化算子是单位算子的非盲图像修复结果

表4 退化算子是模糊算子的非盲图像修复结果

表5 退化算子是单位算子的盲图像修复结果

表6 退化算子是模糊算子的盲图像修复结果

通过对比表3～6中的峰值信噪比值可知，无论是盲图像修复还是非盲图像修复，当退化算子相同时，算法2或算法3中的模型都比现有修复模型的峰值信噪比值高。在非盲图像修复的测试中，算法2 在L1TV_SBM和L0TV_PDA上有了很大的改进。L1TV_SBM与L0TV_PDA和算法2相比，L0范数稀疏性约束比L1范数约束的结果要好一点。L0TV_PDA与算法2对比，算法2对L0范数的求解比L0TV_PDA效果好。在盲图像修复的测试中，由于数据项选用了L0范数的稀疏性先验，算法3的结果优于L02TV_AOP。在相同算法的条件下，模糊算子比单位算子的峰值信噪比值高，恢复的效果较好。

5 总 结

笔者利用L0范数的稀疏性先验和L0范数的等价形式，提出了非盲图像修复模型和基于博弈的盲图像修复模型。模型选用L0范数对数据项或正则项进行约束，使得修复后的结果图与原始图像尽可能接近，适用于无噪声图中缺失区域已知和未知两种情况。基于模型的特性，设计了临近交替方向乘子(PADMM)算法和基于博弈的交替算法进行求解。通过与现有修复模型进行对比，实验结果表明所提出的模型在视觉效果和数值指标上都有较好的结果。

以上主要对无噪声情形设计了模型和算法，并用数值实验验证了模型的可行性。在以后的研究中，将从理论上讨论模型解的性质，进一步探究在此基础上对含有噪声的图像进行修复。