应用统计线性回归的系统误差最大似然配准

李佳炜，江 晶，吴卫华，郑玉军

(1.空军预警学院 预警情报系，湖北 武汉 430019；2.空军预警学院 空天预警系，湖北 武汉 430019；3.中国人民解放军94710部队，江苏 无锡 214000)

协同多传感器系统通过将空间分离的传感器组网协同，可以提高对弹道导弹和卫星等快速目标的探测精度、覆盖范围和截获概率，相比单传感器系统有着更大的潜力和优势[1-2]。然而，系统的融合性能除了受限于传感器各自的探测能力外，还受到固有的系统误差影响。在一定数量级的系统误差下，传统的集中式卡尔曼滤波器[3](Centralized Kalman Filter，CKF)的跟踪性能将严重恶化。因此，为改善系统整体的融合性能，需要首先对系统误差下的多传感器进行配准和补偿[4-8]。

围绕多传感器的系统误差配准问题，国内外学者展开了深入的研究。文献[9-11]针对天基光电传感器，利用恒星期望位置与实际量测的残差，构建关于缓变误差的偏差滤波器和目标状态的非线性估计子，从而实现校正传感器量测的同时估计目标状态。在文献[11]的基础上，文献[12-13]分别将导致视线量测偏差的系统误差描述为姿态失配角和指向偏移角，建立相应偏差矢量的转移模型和已知参考点的量测模型，并通过非线性滤波方法实现对系统误差的在线配准与补偿。上述研究属于在线估计类算法，有良好的实时性，但是需要覆盖范围内参考点的位置信息，而且需要增加用于估计目标状态的滤波器。在离线批处理类算法方面，文献[14]提出适用于两部传感器相对配准的线性最小二乘(Linear Least Squares，LLS)估计子，并给出了其统计性能边界。针对传感器总数大于2的情况，文献[15-16]提出最大似然配准(Maximum Likehood Registration，MLR)算法，其通过似然函数最大化迭代实现系统误差和目标状态的联合估计，且适用于多种传感器观测体制。文献[17-18]针对机动平台的姿态时变情况，构造了能够同时估计传感器量测、平台姿态角系统误差的机动最大似然配准算法。文献[19]推导了WGS-84坐标系下无源传感器量测对目标状态的雅可比矩阵，提出了距离缺失情况下多空基无源传感器最大似然配准算法。文献[20]引入卫星轨道定向、姿态角测量与传感器观测过程中包含的测量误差的先验信息来修正目标状态的误差协方差，进一步提高了最大似然配准算法对多星载光学传感器的配准性能。

然而，上述最大似然配准算法均采用泰勒展开的一阶项来线性化非线性量测转换，其对非线性函数的近似仅达到一阶多项式精度，限制了算法的配准性能。统计线性回归(Statistical Linear Regression，SLR)是一种基于点的方法，其利用多个回归点来近似函数的非线性，能精确到高阶多项式且避免了计算复杂的雅可比或海塞矩阵[21-22]。因此，笔者提出一种基于统计线性回归的最大似然配准算法。该算法利用一组不完全相同的回归点，通过统计线性回归构建目标状态关于去偏量测的回归方程，并得到投影后目标状态的前二阶统计特性；同时利用似然最大化迭代准确求解配准方程，实现对系统误差和目标状态的联合估计。

1 非随机系统误差的最大似然估计

考虑一个协同多传感器系统对共同区域内的同一目标进行连续同步观测，各传感器在观测维度上受到不同程度的系统误差影响，因此系统的量测方程可建模为

zk=h(xk)+b+wk，

(1)

(2)

由于目标状态xk未知，在b和xk均未知的情况下，仅能得到似然函数p(Z|X，b)，其中目标状态集合X={xk∶k=1，2，…，K}。通过联合最大化关于X和b的似然函数，并根据噪声项wk在时域内相互独立，可得X和b的最大似然估计值为

(3)

式(3)也称为系统的配准方程，其中p(zk|xk，b)为量测矢量zk的条件概率密度。

2 统计线性误差传播理论框架

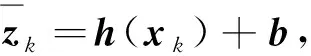
(4)

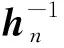
由式(4)可知，目标状态投影误差是由高斯量测噪声经非线性量测转换函数传播后产生的。在系统误差bn已知的条件下，目标状态xk，n的概率密度可近似为一个均值为xk的高斯分布。利用统计线性回归对非线性量测转换进行线性化处理，可近似求得目标状态的一阶、二阶统计特性。

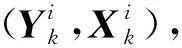
(5)

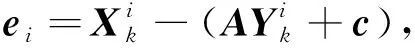
(6)

其中，

(7)

(8)

(9)

非线性函数g的线性化形式可表示为

xk=gL(yk)=Ayk+c+e。

(10)

式(10)也称为xk关于yk的回归方程，其中残差e的均值和协方差矩阵为

(11)

(12)

其中，

(13)

因此，经线性化函数gL传播后的前二阶矩分别为

(14)

var(gL(yk))=AΣykAT+(Σxk-AΣykAT)=Σxk。

(15)

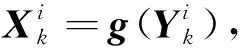
3 基于统计线性回归的最大似然配准算法

(16)

(17)

(18)

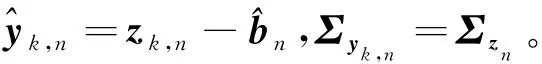
3.1 目标状态估计

使得条件概率密度p(zk|xk，b)在目标状态空间中最大化的xk就是目标状态的最大似然估计。考虑到噪声序列wk，n在传感器间具有相互独立性，则可将p(zk|xk，b)表示为紧凑形式：

(19)

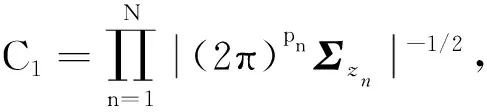
联合式(10)，并忽略线性化误差ek，n的影响，则式(19)在目标状态空间中的近似形式可表示为

p(zk，1，zk，2，…，zk，N|xk，b)≈

(20)

根据式(13)，目标状态误差协方差Σxk，n可近似为

(21)

其中，

(22)

(23)

3.2 系统误差估计

(24)

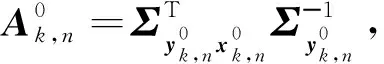
(25)

其中，

(26)

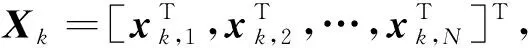
(27)

其中，

(28)

(29)

(30)

其中，

(31)

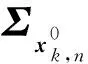
(32)

代入式(27)，式(32)可化简为式(20)的形式：

(33)

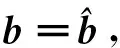
(34)

3.3 算法执行流程

SLR-MLR算法主要由系统误差估计和目标状态估计两个部分组成。算法的具体执行流程概括如下。

输入：历史量测集合Z={zk∶k=1，…，K}。

误差估计：

fork=1，…，Kdo

forn=1，…，Ndo

end for

end for

end while

状态估计：

根据式(27)，计算所有传感器配准后量测在目标状态空间中的投影Xk；

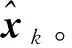
4 仿真实验与性能分析

4.1 场景设置与评价指标

(35)

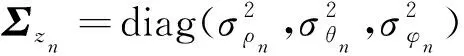
(36)

假设系统在目标发射60 s后开始进行观测，量测采样间隔为1 s，各地面站的地理坐标分别为ϖ1=(120°E，38°N)、ϖ2=(112.5°E，50°N)和ϖ3=(105°E，38°N)。整个系统的观测性能参数如下：各雷达的系统误差分别设置为b1=[2.5 km，3.5°，-1.5°]T、b2=[-1.8 km，-3°，1°]T和b3=[2 km，-2.5°，-1°]T；量测误差标准差均设置为σρn=0.1 km，σθn=0.2°和σφn=0.25°。仿真场景示意如图1所示。

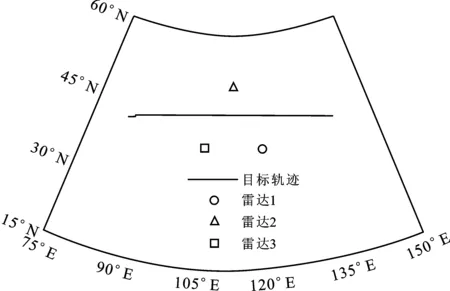
(a) 雷达位置与目标轨迹

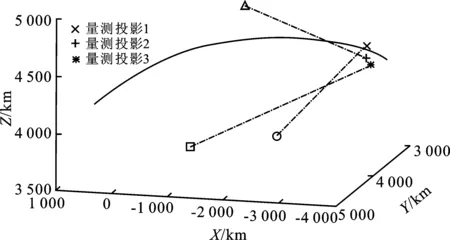
(b) 量测在状态空间中的投影

将系统误差估计的平均误差(Mean Error，ME)和误差标准差(Error Standard Deviation，ESD)作为性能评价指标，来衡量算法对系统误差的配准性能。此外，采用文献[15]定义的克拉美罗下界(Cramér-Rao Lower Bound，CRLB)为性能参考边界。该边界是一个保守值，对于数量不大的蒙特卡罗仿真，能够较准确地评估算法理论上的最优估计性能。注意：系统误差估计的克拉美罗下界的计算需要利用目标状态的真实值xk，其表达式为

(37)

4.2 实验结果与性能分析

仿真实验首先通过单次蒙特卡罗运行，给出了量测采样点数为400时的SLR-MLR配准效果，系统误差估计和目标状态融合结果如图2与图3所示。从配准结果可以看出，算法在迭代次数递增至3～5次后，能较好地收敛到系统误差的预设值附近，并且在任意一个雷达不同观测维度上的估计精度能够达到95%以上。此外，在量测集合经配准补偿后，算法的状态融合结果稳定且接近目标的真实状态。

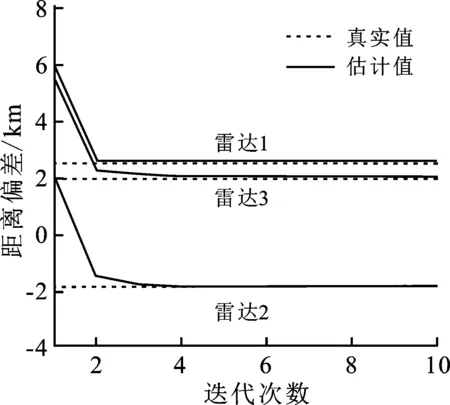
图2 系统误差估计结果

图3 目标状态融合结果

然后，通过100次蒙特卡罗运行，图4和图5给出了迭代总数为5、采样总数为200～400情况下SLR-MLR的配准性能，分别为系统误差估计的平均误差和误差标准差。由图可知，随着采样点数的递增，算法在各个观测维度上的平均误差趋于平稳且收敛于0，误差标准差接近于克拉美罗下界的开平方；在采样总数增加至300后，其稳态平均误差绝对值的算术平均分别为0.153 8 km、0.266 3 km、0.230 7 km，0.007 7°、0.002 9°、0.003 3°，以及0.015 2°、0.010 1°、0.007 2°。结果表明：SLR-MLR能有效地解决协同多传感器系统的配准问题，并且对系统误差的估计是渐进无偏有效估计。

基于上述仿真场景和相同的性能参数，将笔者所提SLR-MLR算法与文献[15-20]采用的基于一阶泰勒多项式近似的最大似然配准算法(Taylor-MLR)进行比较。图6给出了迭代总数为5、采样总数为250～300情况下两种算法对雷达1的配准性能，待测试的SLR-MLR中参数k取值为0、10、20、30、40。图中，SLR-MLR的ESD明显低于Taylor-MLR，并且增大参数k可以明显地改善其配准性能。这是因为Taylor-MLR只能精确到一阶多项式，而利用不敏变换生成加权回归点的SLR-MLR可以达到三阶多项式精度，因此可以更精确地捕捉观测过程的非线性特征以及不确定性。

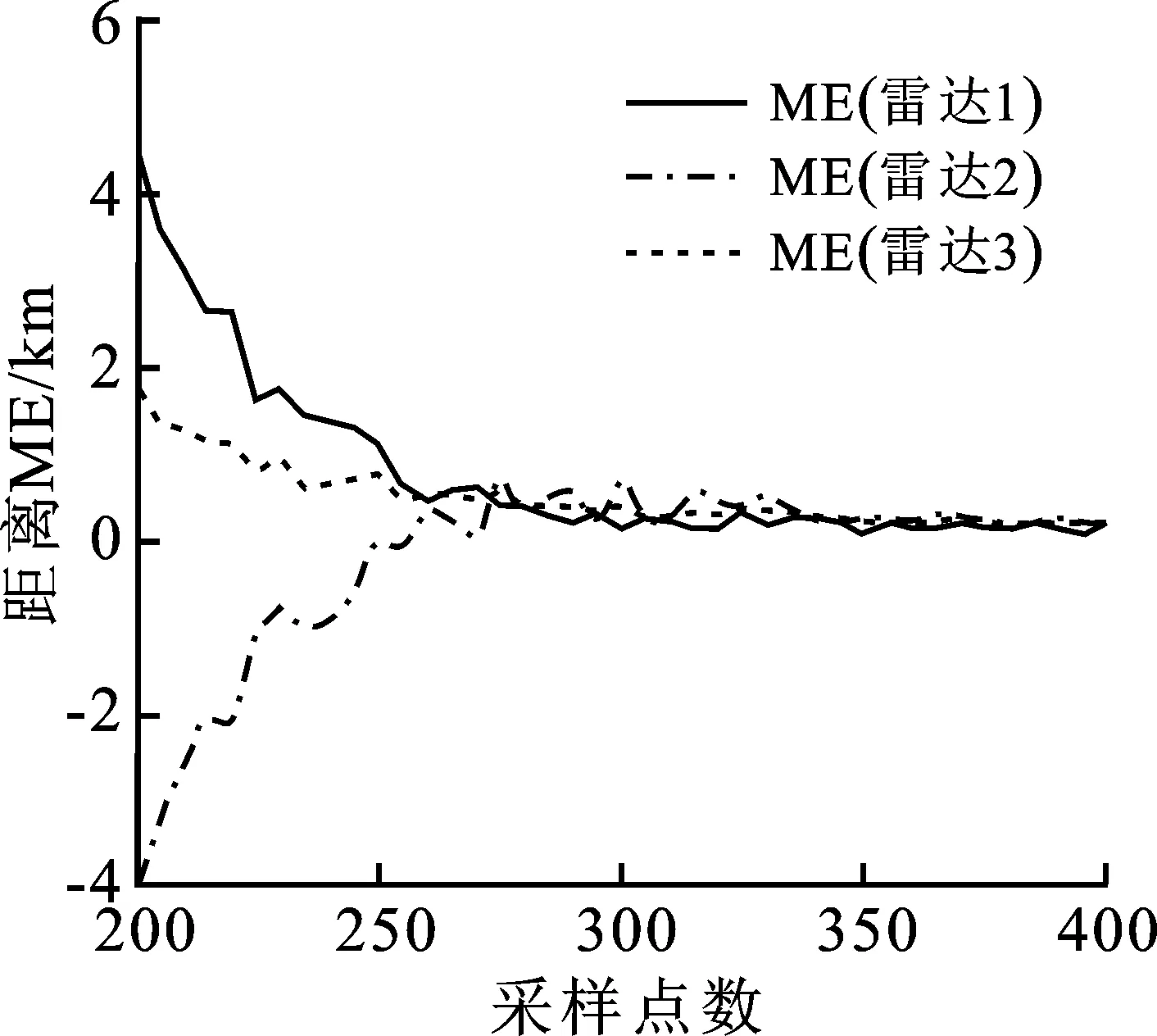
图4 系统误差估计的平均误差

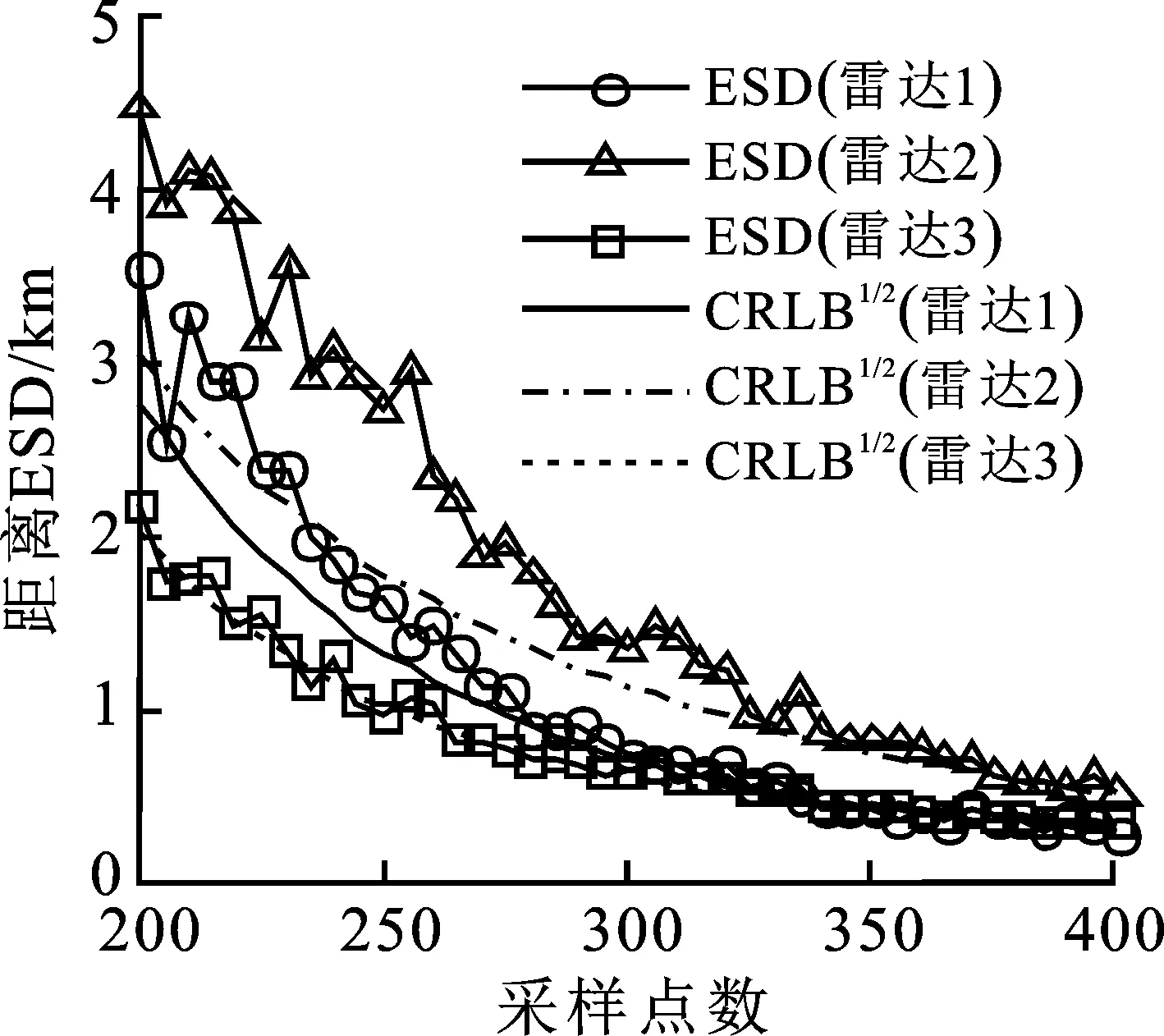
图5 系统误差估计的误差标准差

图6 算法性能比较

为进一步分析参数k对算法性能的影响，图7给出了采样总数为300时不同k下SLR-MLR的配准性能。由图可知，当60≤k≤100时，SLR-MLR的距离ESD和俯仰ESD达到最优，而其方位ESD在k增大到80后开始收敛，因此建议k的取值区间为[80，100]。此外，通过仿真实验可知，两种算法单个配准回路的平均运行时间分别为4.52 s、3.12 s，因此SLR-MLR的计算复杂度约为Taylor-MLR的1.45倍，计算复杂度没有明显增加。

图7 不同参数k下SLR-MLR的配准性能

5 总 结

笔者对协同多传感器系统探测弹道目标情况下的系统误差配准问题进行了研究，提出了一种基于统计线性回归的最大似然配准算法。通过理论分析和仿真实验，可以得到如下结论：(1) SLR-MLR算法能较好地实现对系统误差和目标状态的联合估计，其中获得的系统误差估计是渐进无偏有效估计；(2) 利用不敏变换生成加权回归点，SLR-MLR能达到三阶多项式精度，并且适当增大缩放比例参数可以提升算法的配准性能；(3) SLR-MLR的配准精度高于Taylor-MLR，且计算复杂度没有明显增加，具有一定的实际应用价值。

需要注意的是，所提算法仅适用于静态系统误差的配准场景。对于时变系统误差下的传感器配准问题，采用伪量测方法得到系统误差的闭式表达，再应用递归最小二乘[24]或者递归期望最大化[25]算法，可实现对系统误差估计的动态更新。这也是下一步协同多传感器配准的研究难点和重点。