超密集网络中多基站博弈边缘卸载策略

王汝言，吴 和，崔亚平，吴大鹏，张 鸿

(1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.重庆高校市级光通信与网络重点实验室，重庆 400065；3.泛在感知与互联重庆市重点实验室，重庆 400065)

移动应用和物联网的快速发展，使得仅具备有限电量和计算资源的移动设备已经无法满足当前资源密集型应用的低延迟[1]、高可靠、用户体验连续性等严格要求。为了应对以上挑战，移动边缘计算(Mobile Edge Computing，MEC)应运而生，移动网络运营商和云服务提供商将以合作的形式在网络边缘提供丰富的通信和计算资源，增强移动设备的能力[2]。移动边缘计算允许终端用户通过基站卸载任务至相连的边缘计算服务器，既满足了移动设备计算能力的扩展需求，也减轻了云计算时回程网络的负担，大大减少了端到端的延迟。然而，传统的移动边缘计算网络覆盖密度较小，已很难满足用户日益增长的大数量连接需求；在密集用户区域，中心计算节点的负载量过大，边缘计算服务器中有限的资源会增加任务执行的延迟和能耗，严重影响用户体验[3]。

超密集网络技术通过密集部署低功率小基站，不但可以提高无线网络的覆盖率解决网络覆盖盲点的问题，还可以提升无线网络的容量，缓解用户大规模连接的压力，从而改善网络的整体性能。因此，将超密集网络技术和移动边缘计算相结合的架构成为未来无线接入网发展的趋势[4]。但是，超密集边缘计算网络中的用户处在多个小基站覆盖范围内，用户在同一时间内可访问多个边缘计算服务器，而不同小基站和服务器的资源情况和传输环境不尽相同，使得用户会产生资源竞争和服务器选择的问题[5]，如何为用户进行卸载服务器关联选择以及资源分配来满足用户服务体验具有重要意义。

针对移动边缘计算网络中用户任务的卸载和资源分配，国内外研究人员进行了大量深入的研究。文献[6]利用随机化方法研究了多用户移动边缘计算系统中功耗和延迟之间的权衡，提出一种基于李雅普诺夫优化的在线算法，来解决带有任务缓冲稳定性约束的功耗最小化问题；但该文献的场景只考虑了单服务器的情况，存在无线与计算资源严重短缺，远程云计算访问时间过长的问题。文献[7]在多用户多服务器的边缘计算网络系统中，提出一种基于李雅普诺夫优化的在线动态卸载算法，以获得最小的执行成本和最大数量的卸载任务。文献[8]考虑了一个可再生移动边缘云系统中的多用户多任务卸载调度方案，使用李雅普诺夫优化方法来确定能量获取策略，并提出集中式和分布式两种贪婪算法来解决任务卸载调度问题，但这些文献没有考虑网络资源的分配，降低了系统资源的使用效率。文献[9]研究了多服务器中资源配置和卸载决策的优化问题，提出一种考虑负载分布的启发式算法，在提高服务质量的同时，还降低了边缘计算服务器的能耗和回程流量；但该文献忽略了多服务器下用户的竞争性和自私性，影响用户的卸载体验。

综上所述，研究了在超密集移动边缘计算网络下，将卸载和资源分配与用户自私性相结合的方法，主要贡献如下：

(1) 设计了一种超密集网络下的移动边缘计算架构，将系统效用建模为网络时延和能耗的加权和，联合计算资源分配和任务卸载为一个NP难优化问题。

(2) 提出了一种多基站博弈卸载算法，采用拉格朗日乘数法求解计算资源分配问题，运用匹配博弈理论协调用户与边缘计算服务器之间的相互选择，依据双方偏好效用函数得到最佳的卸载策略。

1 系统模型

1.1 网络模型

(1)

其中，σ2是用户数据传输时的高斯白噪声，B是所接入小基站的信道带宽，Pmn是用户n到小基站m任务数据的传输功率，hm，n是无线信道中的信道增益。

图1 系统模型

1.2 计算模型

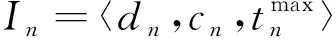
(1) 本地计算

(2)

其中，λ1和λ2分别表示时延和能耗的权重参数，0≤(λ1，λ2)≤1。

(2) 边缘计算

若用户n选择通过小基站中连接的边缘计算服务器执行任务，则其执行的时间由3部分组成：任务数据上传时间、服务器执行时间以及执行结果的回传时间。一般情况下，回传的执行结果远小于任务上传的输入数据，所以忽略任务执行结果的回传时间和能耗[12]。因此，用户任务边缘计算的总执行时间为

(3)

(4)

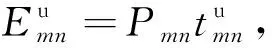
(5)

根据式(2)～(5)，可得系统的总开销为

(6)

2 问题描述

基于上述系统模型，将计算卸载和资源分配表述为优化问题，目标是达到系统开销最小化。显然，要降低整个系统的开销成本，需要为用户找到满足任务要求的最佳卸载决策以及计算资源分配策略，问题描述如下：

(7)

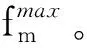
优化问题式(7)中的卸载决策A是一个二进制变量，计算资源F是一个连续变量，使得式(7)是一个混合整数非线性规划问题，从而是一个NP难问题[13]。为有效解决大规模设备的系统优化的NP难问题，已有许多研究采用了问题分解的次优化方法。因此，根据式(7)的目标函数和约束条件的结构，可以将式(7)分解为目标和约束分离的两个子问题[5]。子问题1是在给定卸载下的计算资源分配问题：

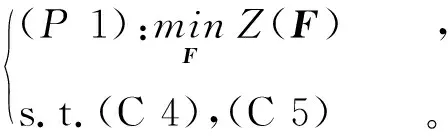
(8)

子问题2是在给定计算资源分配下的卸载决策问题：

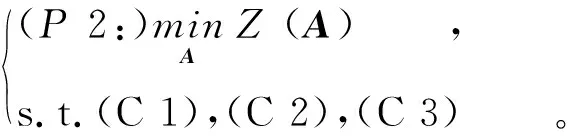
(9)

多基站博弈卸载算法使用拉格朗日乘数法和匹配博弈论来寻找最优的F和A，通过确定最优的F和A可以寻找式(7)的最优解。

3 多基站博弈卸载算法

该部分提出了多基站博弈卸载选择算法。该算法首先利用拉格朗日乘数法解决子问题1，然后子问题2先转化为用户-服务器匹配问题，根据子问题1得到的计算资源分配解，进一步采用匹配博弈卸载求解。每个用户都需要得到自己的任务处理结果，并期望该任务处理的开销尽可能小。由此，对于每个用户独立进行任务决策是非常合理的，他们可以根据本地终端的资源以及可利用的网络资源自行决定任务的处理方式。同理，不同的边缘计算服务器之间没有相互耦合，可以独立地控制与管理其所服务范围内的用户。

3.1 计算资源分配

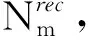
(10)

定理1计算资源分配问题是一个凸函数。

证明：通过求导，可得

(11)

(12)

因此，式(10)为一个凸函数，详细的证明可以参考文献[14]。另外，其约束条件C 4和C 5都是线性的，使得式(10)为一个凸优化问题，依据KKT(Karush-Kuhn-Tucker)优化条件，最优解可以通过拉格朗日乘数法求得。对于边缘计算服务m所服务的用户n的计算资源分配的最优解为

(13)

在求解子问题1后，需要进一步解决子问题2，才能得到系统开销最小的解。下面在3.2和3.3节详细描述该卸载决策问题。

3.2 用户与服务器匹配

对于子问题2，边缘计算服务器的选择很大程度上影响任务的卸载决策，用户需要比较本地终端与多个服务器的处理开销，从而确定最佳的卸载策略。为保证所有用户的卸载公平性，设置了一种卸载决策机制，先假定所有的用户任务都进行卸载处理，在其选定最优的卸载服务器之后，再与本地终端计算进行比较，从而决定最终的卸载决策。此时，卸载决策问题可以转化为用户与服务器的匹配问题：

(14)

在求解用户与边缘计算服务器的匹配问题时，常常会选择就近卸载的方案，考虑到满足用户体验，这可能会造成某些服务器负载较重或者某些因负载较轻而造成空耗现象的发生。如果能在用户和服务器两者匹配时进行双向选择，则可能达到一个最优的匹配。

匹配博弈论是一种广泛且强大的方法来有效地模拟两组成员之间的交互过程；考虑到用户以及边缘计算服务器的自私性与合理性，双方都会根据自身的偏好找到双方最优的选择结果，将匹配博弈理论应用到用户与服务器匹配问题来进行组合问题的分布式求解是非常可行的[15]。在超密集边缘计算网络系统中，一个用户只能选择一个服务器进行卸载，而一个服务器可以同时接受多个用户的卸载请求，实现了多对一的匹配方式。为准确描述用户与边缘计算服务器之间的匹配关系，定义了一个多对一的匹配对，对于给定的匹配对用户n∈N以及服务器m∈M满足以下条件：

(15)

其中，条件①表示用户n所匹配到的服务器是其所能连接到的服务器集合Mn之一；条件②表示服务器m所匹配的用户是其所覆盖范围内的用户集合Nm之一；条件③表示用户n所匹配的服务器最多不能超过一个；条件④表示用户n与能够与服务器m建立匹配，那么服务器m同样也能够与用户n建立匹配。

3.3 多基站博弈算法

每一个用户以及边缘计算服务器匹配过程中需要考虑关联要求，匹配关联算法允许用户和服务器首先定义自身的偏好效用函数。为了找到稳定的匹配，需要根据偏好效用函数构建自己的偏好列表。

(1) 用户偏好：在进行多服务器选择时，用户在综合考虑多项偏好因素下，包括用户与所连接边缘计算服务器之间的距离、信道增益、噪声干扰等，会选择传输速率较高的服务器，这不仅减小了数据的传输时延，也降低了传输的开销。除此之外，利用子问题1求得的用户资源分配解，在等待处理结果回传时，也需要其闲置等待的开销尽可能少，则用户的效用函数Φn，P(m)为

(16)

(2) 边缘计算服务器偏好：服务器挑选卸载用户时，会尽可能考虑任务数据上传时间较少的用户，避免服务器预留给该用户计算资源的闲置时间过长，从而提高计算资源的利用率。则边缘计算服务器的效用函数Φm，P(n)为

(17)

多基站博弈卸载算法具体描述如下：

算法1多基站博弈卸载算法。

③ forn=1 to |No| do

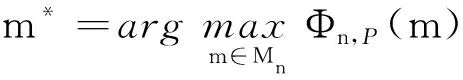
⑤ 设置kmn=1发送卸载请求给服务器m

⑥ end for

⑦ form=1 toMdo

⑨ 通过式(17)设置服务器的偏好

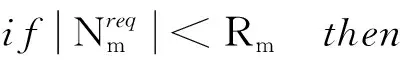
4 仿真分析

4.1 仿真参数设置

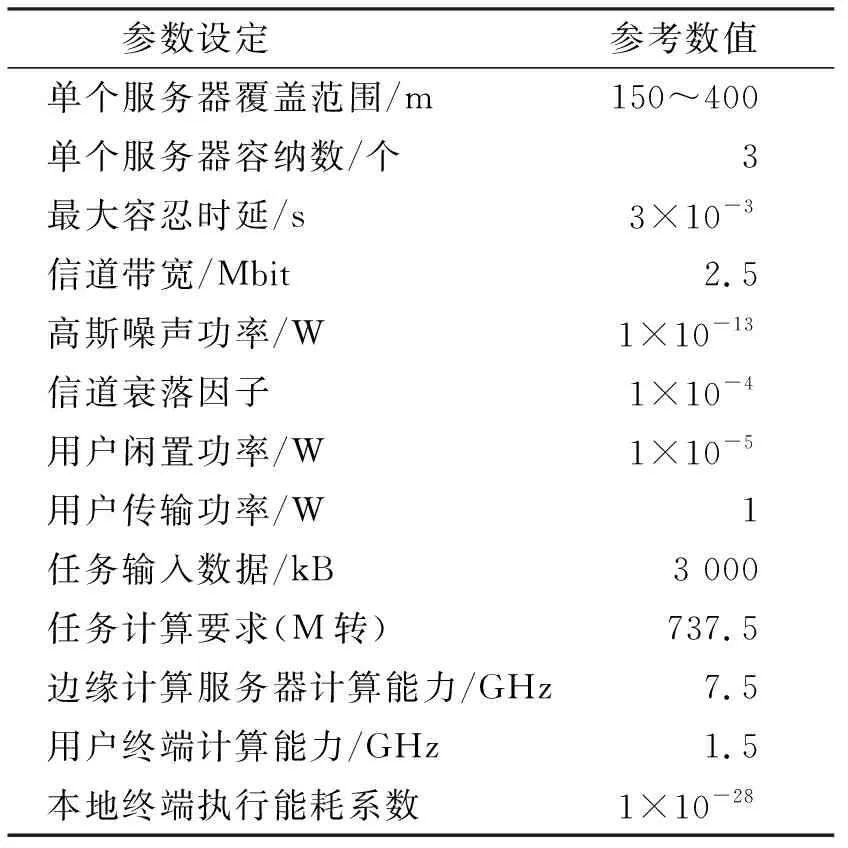
表1 仿真参数设置

采用Python仿真平台对所提出的算法进行性能评估。仿真环境是基于EUA数据集设计的，其中包含墨尔本CBD区域内125个边缘基站以及在内的816个用户的实际地理位置[16]。为了更进一步模拟真实环境，进行了移动性设置，即每个用户会在每个时隙中进行位置的随机更替。仿真默认参数如表1所示。

因开销定义为用户任务处理和时延的加权和，所以开销无量纲。为了验证算法的优劣性，引入文献[17]中3种代表性的基准算法进行对比。

(1) 随机卸载：每个用户的任务随机进行本地执行或者部分分割卸载给边缘计算服务器。

(2) 贪婪通信卸载：每个用户的任务将会选择最近的边缘计算服务器进行卸载，如果一个用户所挑选的服务器已经分配给其他用户，那么该用户将会选择信道增益次之的服务器。

(3) 贪婪计算卸载：每一个用户的任务都分割卸载给边缘计算服务器，尽可能地利用服务器的资源。

4.2 仿真结果分析

图2显示了20个边缘计算服务器，40个用户场景下4种算法不同时隙用户的平均开销，其中单个时隙为3×10-3s。多基站博弈卸载在每个移动的时隙基本能够稳定在一个较低开销，相对于贪婪通信卸载，随机卸载和贪婪计算卸载平均可节省14.50%、20.70%以及28.66%。贪婪计算卸载由于采用全部卸载方式，分配的带宽被多移动设备所共享，从而造成通信速度大大降低，开销高于能够随机进行本地处理的随机卸载。贪婪通信卸载虽然也采用全部卸载的方式，但其性能优于随机卸载和贪婪计算卸载而逊于多基站博弈卸载，是因为在贪婪通信卸载考虑了最佳的信道增益，降低了任务传输的开销，说明通信传输对于开销有较大的影响。

图3显示了20个边缘计算服务器下系统开销与用户数量的关系图。随着用户数量的增加，4种算法的曲线都呈上升趋势，在相同用户数量下，所提出的多基站博弈卸载的系统开销最小。在用户数量较小，如为20时，多基站博弈卸载、贪婪通信卸载、随机卸载和贪婪计算卸载的开销相近，多基站博弈卸载开销节省分别为9.507%，16.220%，20.990%。这是因为此时通信与计算资源充足，相比于本地计算，用户更倾向于进行任务卸载，使得开销差异不明显。当用户数量增加为40时，多基站博弈卸载开销节省分别为14.50%、20.70%以及28.66%。这是因为卸载用户对边缘计算服务器中有限的通信资源和计算资源相互竞争，用户平均资源分配低，增加了系统的开销。尤其是贪婪通信卸载，由于每个服务器只能接收一个用户任务，通信资源紧缺，使其开销增长迅速。而多基站博弈卸载依据低开销的效用函数，充分地利用本地终端资源，减小通信资源的竞争，同时进行计算资源的合理分配，从而保持较小的开销增长。

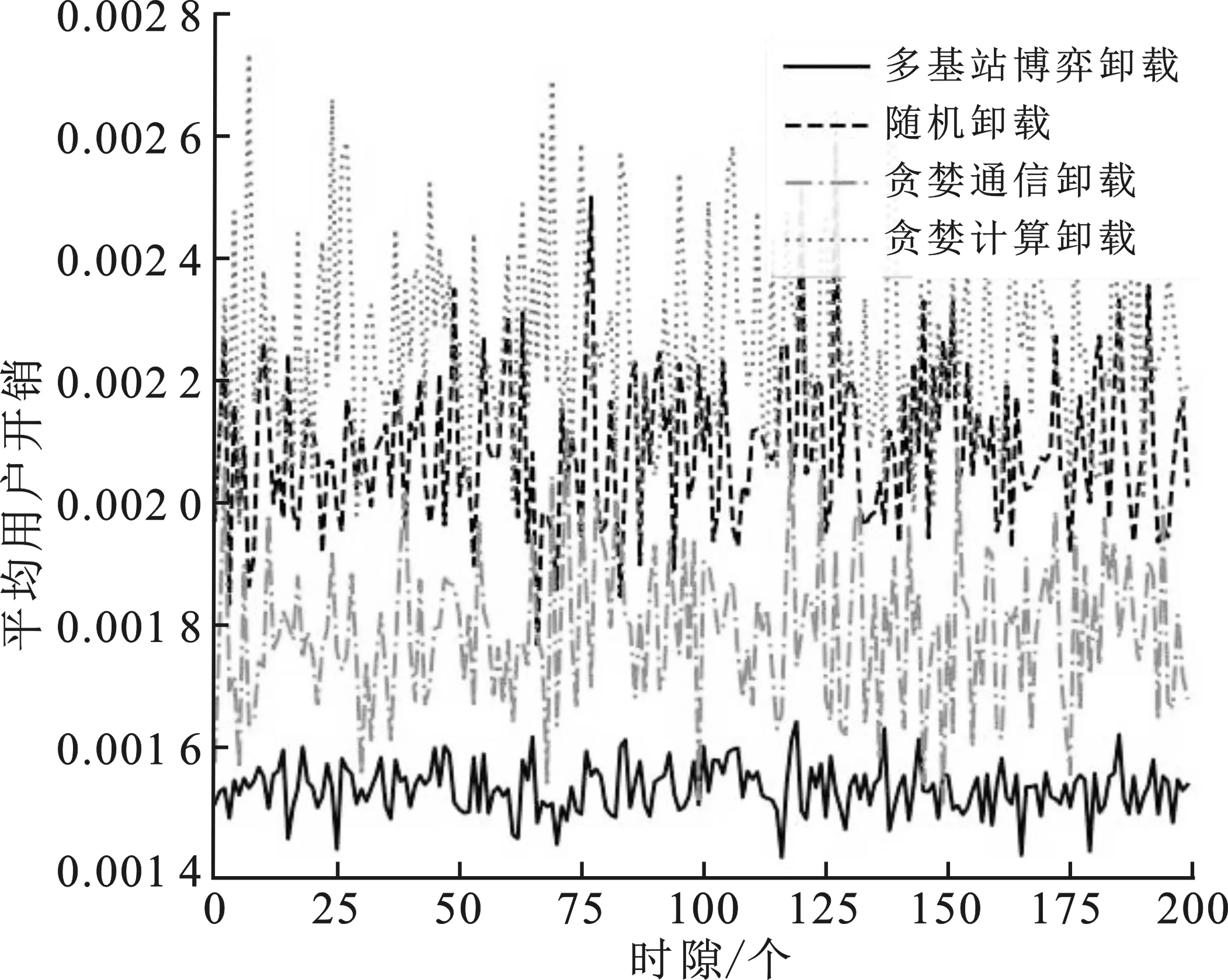
图2 用户平均开销与时隙的关系

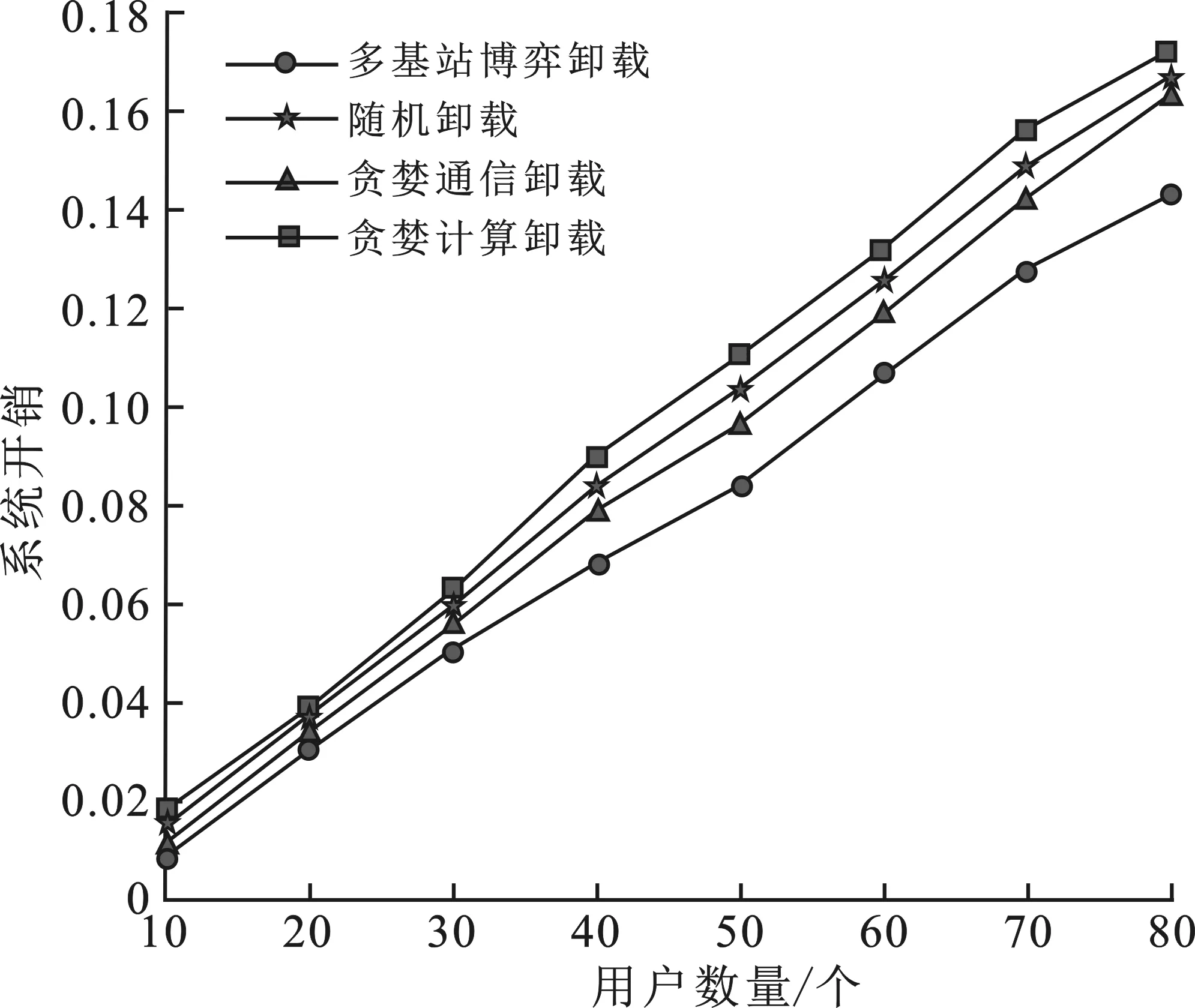
图3 系统开销与用户数的关系

图4显示了系统开销随任务输入数据大小变化的曲线。随着任务大小的增加，4种算法都呈上升趋势。当任务输入数据较小，设置为1 500时，随机卸载的开销要小于贪婪通信卸载，分别为0.052 92和0.055 50。这是因为此时本地终端的计算资源有足够的能力完成任务，而无线传输加上边缘计算开销较大，贪婪通信卸载和贪婪计算卸载因必须卸载而产生了较大的开销，而且随机卸载因兼具本地与卸载两种任务处理方式，使其一开始开销低于贪婪通信卸载，多基站博弈卸载尽量通过本地完成任务，从而开销较低。而随着任务输入数据地进一步增大，本地终端的计算资源已难以成功完成任务并且开销较大，必须将决策方式改为卸载才能减小系统开销。此时，贪婪计算卸载由于全部卸载特性，开销始终大于随机卸载。而优化信道增益的贪婪通信卸载逐渐优于随机卸载，但贪婪通信卸载因缺乏计算资源的分配，使其开销始终要高于多基站博弈卸载。

图5显示了60个用户场景下，系统开销随边缘计算服务器数量变化的曲线。服务器数量较小，服务器数量为10时，多基站博弈卸载、贪婪通信卸载、随机卸载和贪婪计算卸载的开销相近，分别为0.110 2，0.121 0，0.120 9，0.124 8。这是因为所选服务器的数量有限，卸载可选的方式较少，使得4种算法开销相差较小。随着服务器数量的不断增加，随机卸载和贪婪计算卸载的开销呈上升趋势，这是因为更多的服务器选择使得存在任务分割机制的随机卸载和贪婪计算卸载所连接的服务器更多，从而增大了传输开销。而多基站博弈卸载和贪婪通信卸载的开销呈下降趋势，这是因为它们能够从增多的服务器中挑选最佳的服务器机会更大，使得系统开销不断减小，但当服务器数量达到80时，多基站博弈卸载和贪婪通信卸载的系统开销分别收敛为0.059 5和0.074 2，此时意味着当服务器数量达到一定量时，多基站博弈卸载和贪婪通信卸载所选的最优服务器都不会再变化。

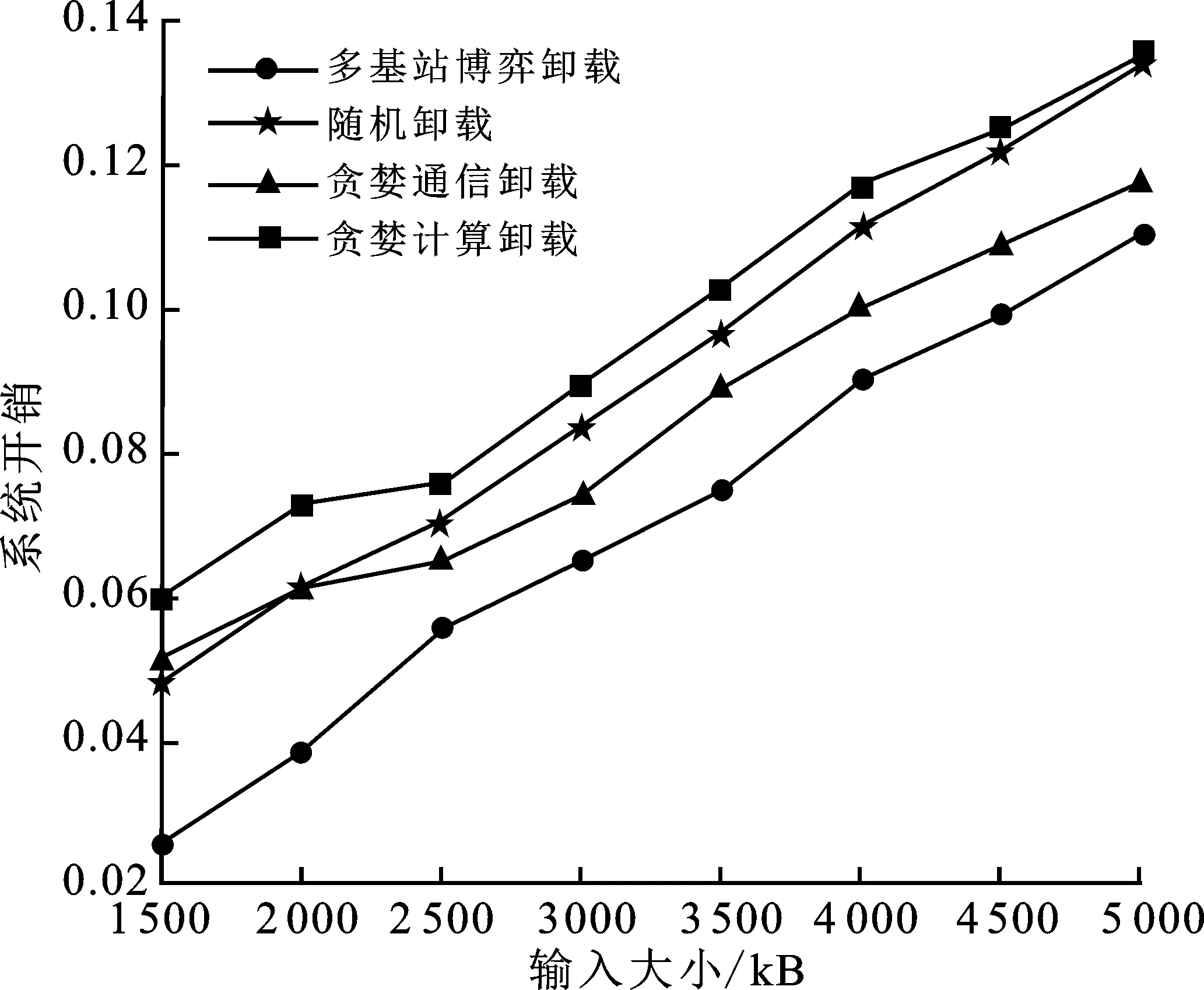
图4 系统开销与任务输入大小的关系

图5 系统开销与服务器数的关系

图6 系统开销与服务器容纳数的关系

图6显示了20个边缘计算服务器，100个用户场景下系统开销随服务器容纳数变化的曲线。当容纳数为1时，无计算资源分配优化，多基站博弈卸载、贪婪通信卸载、随机卸载和贪婪计算卸载的开销相近。随着容纳数的进一步增加，贪婪通信卸载由于服务器只能容纳一个用户，使其开销几乎不变，稳定在0.199 2。随机卸载和贪婪通信卸载存在全部卸载机制，由于增加容纳数从而对通信与计算资源的竞争加剧，使其开销不断增大。多基站博弈卸载存在低开销的卸载机制与计算资源分配策略，使其在容纳数增加的初期降低开销，但随着容纳数的进一步增加，用户间的资源竞争使其停止了继续接收用户卸载，从而使系统开销基本保持不变，收敛在0.158 4。

通过对上述仿真结果分析可以看出，相对于其他算法，提出的多基站博弈卸载算法可以有效降低系统开销成本。这是因为该算法使用了拉格朗日乘数法和匹配博弈的方法对系统进行了优化。性能的增益主要由计算资源分配和自私卸载选择两部分得到。首先是计算资源分配，使用拉格朗日乘数法，在任务最大容忍时延之前，为各边缘计算服务器的计算资源进行合理分配，提高资源的利用效率。其次是自私性选择，使用匹配博弈的方法，一方面为用户寻找所偏好的边缘计算服务器，另一方面也为服务器选择效益较高的用户，实现用户与服务器的最佳双边匹配。综合这两部分，相对于其他传统算法，提出的算法通过协调最佳用户与服务器的配对，同时又进行各服务器计算资源的分配优化，减少了资源的浪费，从而比传统算法节省系统开销。

5 结束语

设计了一种超密集网络下的移动边缘计算架构，考虑到最小化边缘计算网络系统的开销，将优化问题分解为计算资源分配和卸载决策两个子问题，并提出一种多基站博弈卸载算法，利用拉格朗日乘数法求解计算资源分配问题，运用匹配博弈理论协调用户与边缘计算服务器之间的相互选择，依据双发偏好效用求得最佳的卸载策略。仿真结果表明，提出的多基站博弈卸载算法相对于3种基准算法，可有效节省系统开销。另外，当用户数量增多或任务输入尺寸增大时，多基站博弈卸载算法的系统开销会增大，而当服务器数量增多或服务器容纳数增多时，多基站博弈卸载算法的系统开销会逐渐减小直至收敛。