水下机器人姿态融合算法研究
2021-09-01朱明明辛绍杰邓寅喆
朱明明,辛绍杰,邓寅喆
(上海电机学院机械学院,上海201306)
随着人类探索海洋资源速度的加快,勘探海洋资源已成为各国重要的战略目标[1]。水下遥控机器人(Remotely Operated Vehicle,ROV)操作简单、响应快,可以辅助人类在水下复杂环境中执行特殊任务。当前,ROV的导航主要有惯性导航、水声学导航、声呐导航以及航位推算导航等[2-4]。其中惯性导航系统误差会随时间而逐渐累加,如果没有其他导航传感器数据信息定期修正导航误差,会产生极大的偏差[5]。卢峰等[6]提出利用水声学传感器进行水下导航,能够解算出ROV在水下作业时较为准确的位置信息,但该方法水下作业距离有限,限制了ROV自主作业能力以及运行范围。孙玉山等[7]采用ROV航位推算导航系统,分析了航位推算导航系统存在的推算误差,并没有解决导航传感器自身数据采集时带来的误差。高延增等[8]提出了融合短基线定位声呐实现ROV定位,只是模块化地设计了ROV定位系统,以定位算法实现定位,但并未处理声呐信号噪声,无法有效降低声呐自噪声和水体噪声对ROV定位的影响。马剑等[9]提出将卡尔曼滤波(Extended Kalman Filter,EKF)算法应用于ROV超短基线定位中,却忽视了算法存在精度差、数据噪声大等问题。
针对以上问题,本文提出基于四元数的改进EKF算法,并通过理论设计和实验仿真对导航精度进行验证。结果表明,使用改进EKF算法可提高ROV姿态融合精度,改善了目前多传感器融合算法数据处理的一些不足。
1 导航结构设计
本文采用自主设计的结合水面无人艇协同作业的便携式水下机器人(Unmanned Surface-Remotely Operated Vehicle,US-ROV)见 图1。US-ROV通过脐带缆将水面操纵台与ROV相连,脐带缆为ROV提供动力并进行信息交互。USROV是一种新型的ROV,是未来水下工程检测与特种作业的关键设备。

图1 便携式US-ROV
导航系统传感器部分主要由惯性测量单元(Inertial Measurement Unit,IMU)组成,用来采集ROV的实时姿态信息。信息传输给控制模块,用改进EKF算法进行ROV的姿态解算,同时为了防止GPS信号在水下丢失,需要水面无人艇进行GPS信号校正。导航系统结构如图2所示。

图2 导航系统结构
2 导航算法设计
2.1 EKF
ROV导航系统利用安装的姿态传感器获取姿态信息数据,通过姿态解算确定其位置信息[10]。经状态估计算法融合各类传感器数据,通过坐标转换解算出ROV姿态信息。较为常用的状态估计算法为EKF[11]。EKF是通过最大似然估计在系统状态过程中状态向量近似估计的优化算法。US-ROV姿态导航采用传统EKF时的状态模型方程和状态更新方程如下:
(1)时间更新

式中:Rk+1为测量噪声在k+1时刻的协方差矩阵;Kk+1为k+1时刻的卡尔曼增益矩阵;Hk+1为状态变量到测量的转换矩阵;而

为在k+1时刻所求得的系统状态协方差矩阵;
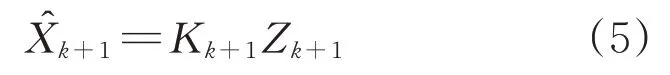
为在k+1时刻所求得的系统状态估值。
由于水下作业不能设置静态零速进行惯性导航系统采样误差修正[12],因此需要采用高灵敏度传感器进行ROV的姿态解算,但即使高灵敏度的传感器仍然存在测量误差。
由于传感器采集到的数据会有很大的噪声干扰,使输出结果误差较大。例如,加速度计传输的加速度信息需要经积分运算才能转换到速度信息。因此,这种发散影响会随着数学运算进一步增强[13]。虽然利用EKF可以根据当前状态和上一时刻的状态作为对比预,测输出结果,在一定程度上优化了传感器采样值。但传统EKF进行多传感器信息融合仍然存在数据噪声大、误差较为明显等问题[14-15]。
2.2 改进EKF
针对采用EKF进行多传感器信息融合存在的误差大、噪声扰动大等问题。本文对EKF进行改进,着重探讨以四元数为状态量,进行基于四元数的改进EKF设计。
首先,根据系统需求建立EKF的非线性状态方程:

式中:xk为k时刻的系统状态变量;xk-1为k-1时刻的系统状态变量;A为状态转移矩阵,负责将k和k-1时刻的状态联系起来;N(0,Qk)假定为零均值、方差为Q的高斯分布过程噪声函数。而
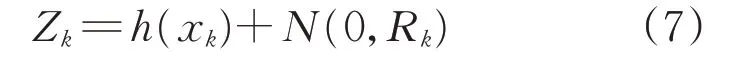
为k时刻的系统观测量;h(xk)为观测模型,可将状态量xk转换到Zk中;N(0,Rk)假定为零均值、方差为R的高斯分布观测噪声函数。
根据式(6)和式(7)得出系统的EKF非线性方程,然后分析基于四元数的改进EKF方程。由四元数的定义可知,四元数是由4个元素构成的四维向量,用来表示载体在三维空间中的姿态方向信息,有

式中:q0、q1、q2、q3为实数;q0为实部;q1i+q2j+q3k为虚部。
基于四元数的改进EKF,建立状态向量为
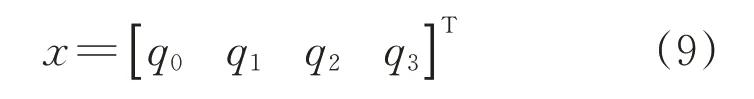
式中:q0、q1、q2、q3为姿态信息的四元数。
初始化为
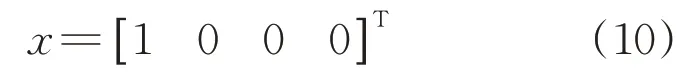
初始化即默认载体的横倾、俯仰、偏航3种姿态角都是从0°开始。
建立非线性状态方程并完成初始化后,系统预测模型为
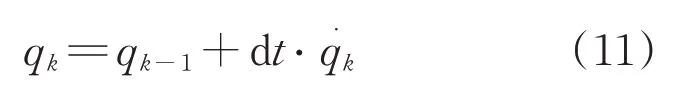
式中:qk-1为k-1时刻的四元数;qk为更新后k时刻的四元数。
得出预测模型后,需要知道四元数微分方程,四元数q的微分方程为
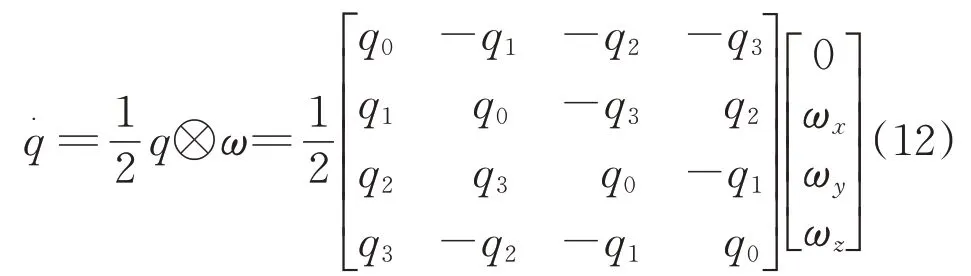
式中:ω=[0ωxωyωz]T为数据融合后运动坐标系下的三轴角速度;ωx为x轴角速度;ωy为y轴角速度;ωz为z轴角速度。
根据式(12)和式(6)可以得出系统预测模型为

通过雅可比矩阵线性化得到状态转移方程为

式中:F为四元数更新对ROV角速度状态转移矩阵。
根据式(14)求出状态转移方程后,对观测量进行分析。为简化推导过程,仅对姿态信息中的加速度计测量重力在运动坐标系下的三轴分量作为观测数据进行分析。加速度计观测数据为
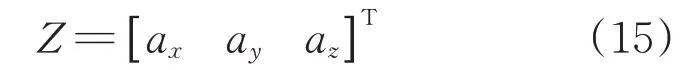
式中:ax、ay、az为加速度计在运动坐标系下的三轴分量;
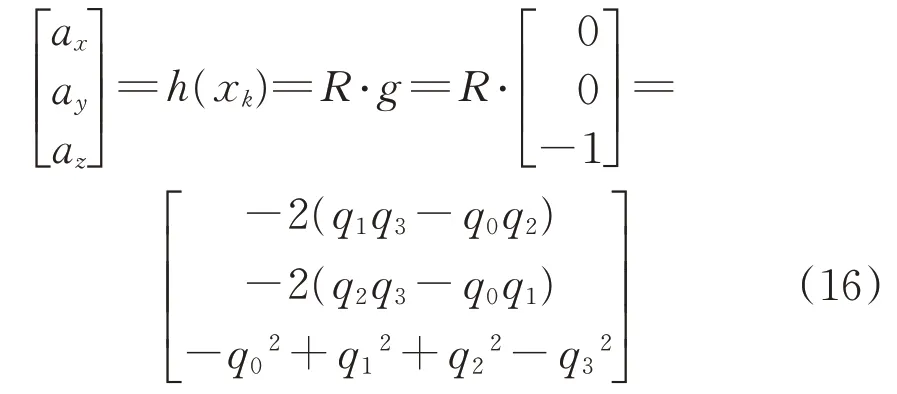
为观测模型;g为重力加速度,是大地坐标系下的坐标向量,需要坐标转化到载体坐标系下;R为旋转矩阵,从地面坐标系转化到运动坐标系;h(xk)为观测模型,与前面的预测模型一样进行线性化处理。线性化的观测模型为

由于本文只对姿态信息中的加速度计测量重力在运动坐标系下的三轴分量作为观测数据进行分析,所以H即为系统得到的总的观测矩阵。
3 实验仿真
ROV下水实验如图3所示。实验测得的ROV姿态数据,经改进EKF算法解算可使姿态数据更为精准,达到对ROV精准控制的目的。

图3 ROV下水实验
对于实验测得的数据,经程序仿真观测改进EKF的数据处理效果。通过预测模型与观测模型的理论分析,改进EKF程序设计步骤如下:

按上述步骤,将实验数据输入程序进行仿真。通过两组实验对改进EKF进行对比分析。坐标系根据坐标转换规则,转到前右下坐标系中,并使横倾角速度对应到x轴,俯仰角速度对应到y轴,偏航角速度对应到z轴。在程序中用gx=rollrate、gy=pitchrate、gz=yawrate来实现坐标系的对齐。取两组实验数据进行仿真验证,其中多传感器信息的算法融合运用到了陀螺仪、加速度计以及磁力计传感器。由于地磁计数据的加入使得实验中偏航角并不是从零开始。
第1组实验将传统EKF与参考值进行对比分析,分别与横倾、俯仰、偏航3种姿态角进行对比,分析EKF对于3种姿态角的影响。图4为EKF与参考值对比。
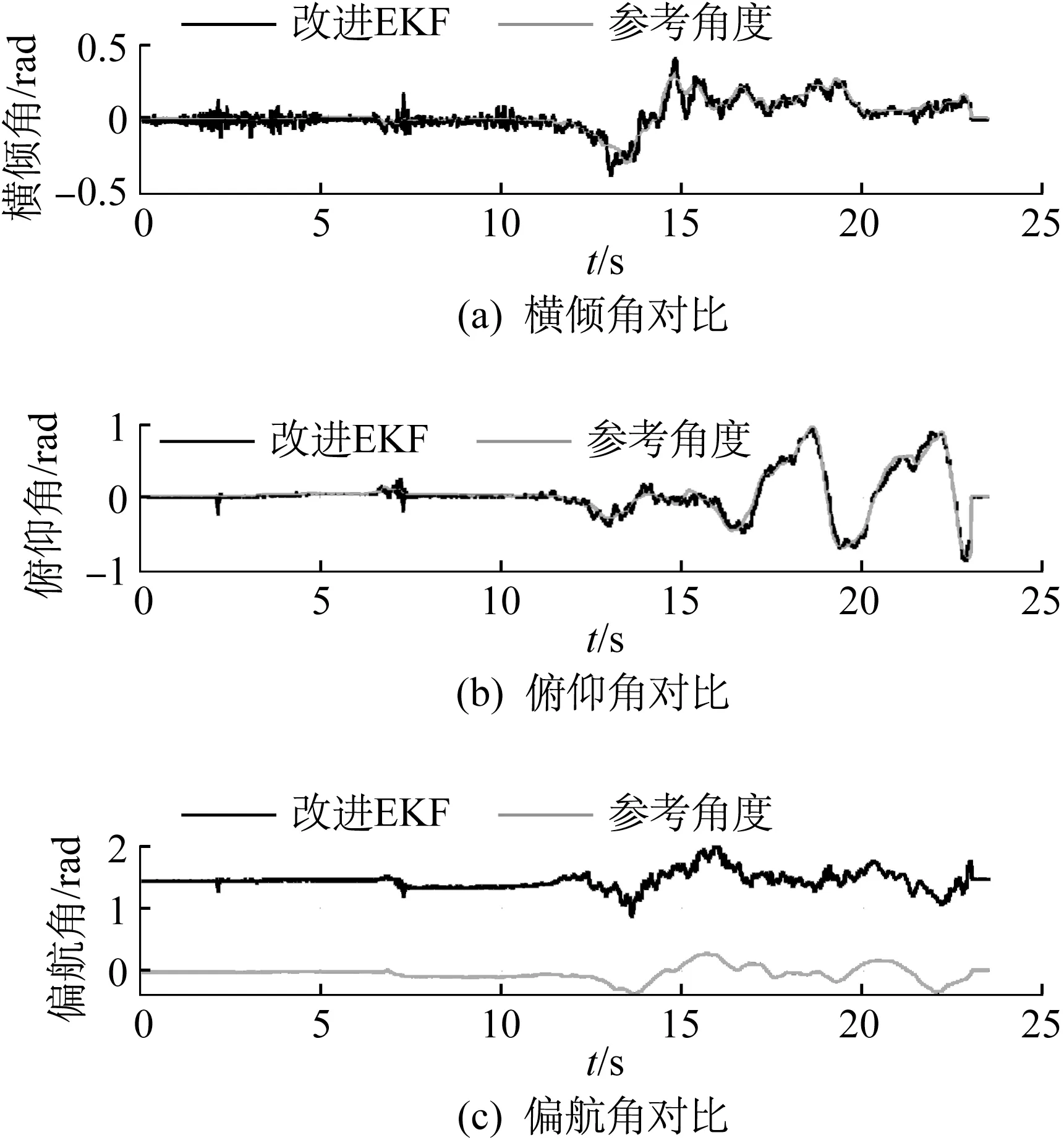
图4 EKF与参考值对比
第2组实验将改进EKF和参考值进行对比分析,验证改进EKF的优点。图5为改进EKF算法与参考值对比。

图5 改进EKF与参考值对比
采用改进EKF和传统EKF分别与参考值对比,如表1和表2所示。通过对比分析可知,传统EKF会有一定程度的噪声干扰,而改进EKF不仅能在动态响应上符合要求,而且能很好地处理数据噪声,使姿态数据曲线更加光滑。

表1 改进EKF与参考值对比

表2 EKF与参考值对比
4 结 语
针对ROV使用EKF进行姿态融合解算中存在的噪声误差问题,在基于四元数姿态解算算法的基础上和EKF进行结合,改进EKF在精确性和实时性上均优于传统EKF。仿真实验表明,改进EKF可以精确处理数据,系统收敛性得到提高,可以满足水下机器人在复杂海域条件下作业的需求。
