基于分形理论的剩余电流互感器故障类型判断
2021-09-01贾云翔迟长春耿晋中
贾云翔,迟长春,耿晋中
(上海电机学院电气学院,上海201306)
剩余电流互感器作为智能漏电保护器的一个核心部分,对漏电保护器防止漏电事故起着重要作用,需要对其定期检查维持稳定运行。由于工作环境噪声大、检查过程繁琐、判断结果依据不够全面等原因,给故障判断增加了很多难度和干扰,需要加快诊断手段的研究。如今国内外对于故障诊断研究,采用分形理论分析的领域越来越广泛。文献[1-4]对设备故障诊断研究采用分形理论进行分析,很好地改善了故障诊断流程。文献[5-6]在故障诊断时应用盒维数计算方法,减少了诊断结果所需确认时间。文献[7-11]在输出特征信号采样前采用小波阈值降噪法降噪,极大地改善了输出信号波形。文献[12-16]中故障诊断以盒维数为故障类型判断依据,提高了判定故障结果的精确率。
在对剩余电流互感器故障输出波形采集信号时[17],通过新小波阈值降噪法保持初始信号特征,同时建立故障输出波形数学模型。在不同故障因素下,利用计算快速的网格维数计算盒维数,建立以盒维数为主,极值幅值为辅的判断方法,快速精确判断出剩余电流互感器存在的故障类型,对剩余电流互感器的稳定运行有着重要意义。
1 理论基础
1.1 分形理论
分形理论作为剩余电流互感器故障判断研究理论基础,有着和剩余电流一样的自相似性,部分和整体之间的特征总是存在相似性。因此,分形理论用于研究剩余电流互感器故障类型有很好的实用性。分形维数作为刻画剩余电流输出信号的特征值,通常分为关联维数、盒维数、广义维数等多种维数,其中盒维数计算简单且表达形式直观,故将其应用于采集无规则剩余电流信号上,常用表示方法为
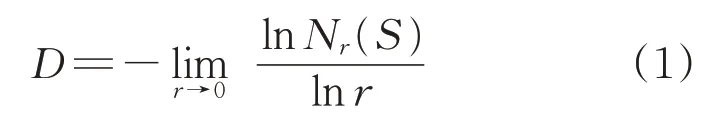
式中:D为盒维数;r为正方体盒子边长;S为非空有界子集;Nr(S)为填充空间所需盒子数。
1.2 盒维数计算过程
采样剩余电流得到的信号是有时间序列的一维曲线f(x),此时对信号处理可用等价盒维数的网格维数。设采样所需总时间为td,每个时间段∆t采集的信号为xi,依据时间段可得样本数n=td/∆t。其中,xi差值便是分形理论中的所需填充空间大小,时间间断是分形理论中的填充空间盒子大小。因此,网格维数很好地将分形理论盒维数方法运用到剩余电流信号采样中,其中,网格高度设为H,描述故障剩余电流分形特征的网格维数表示为
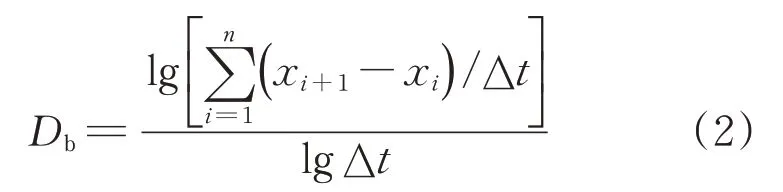
计算Db时,将已经划分出的样本数依据新网格直径ε再划分,之前划分的区间被再一次划分成更多子区间。在子区间内计算最大离差
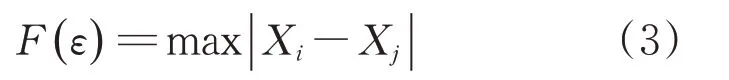
找到子区间内离差最大的两个样本Xi和Xj相减即可,同时得出总样本数
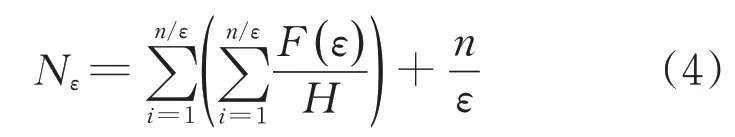
将ε扩大m(m=2,3,…,a,aε≤n)倍,用同样的方法计算a-1个时间序列曲线的离差和样本数,则盒维数D可用Db计算得到,用平均法计算如下:
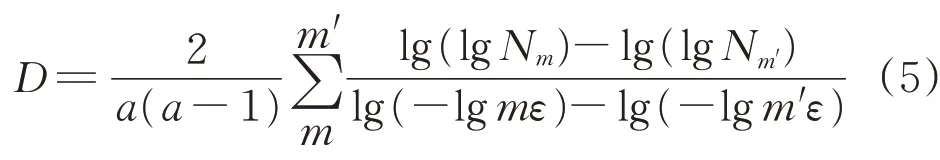
式中:m,m'=2,3,…,a,且m'>m。
2 新小波阈值降噪法
在对剩余电流互感器输出波形信号处理时存在噪声干扰问题,很难得到初始信号。传统硬、软阈值降噪法处理后的信号有间断不连续和恒定偏差的问题。为解决这些问题,提出新小波阈值降噪法进行优化。


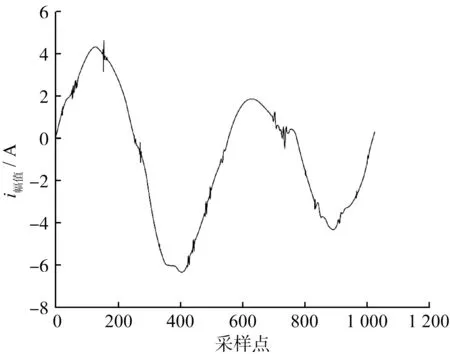
图2 软阈值法降噪
由图1~图3对比可知,新阈值降噪法很好地解决了软、硬阈值降噪法恒定偏差和非连续性问题,波形更为光滑。一般来说,信噪比越高,均方差越小,去噪效果越好,更能接近初始信号。为了进一步试验3种降噪方法的降噪效果,对含噪信号进行分解,并用最小极大方差法确定阈值,经Matlab仿真将信噪比和均方差作为对比基准,如表1所示。通过计算发现,新阈值法信噪比最高,均方差最小,验证了新阈值降噪法的优越性和降噪效果。
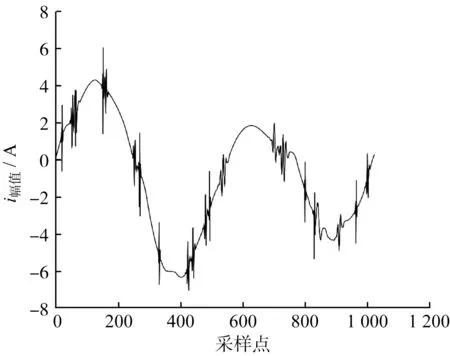
图1 硬阈值法降噪
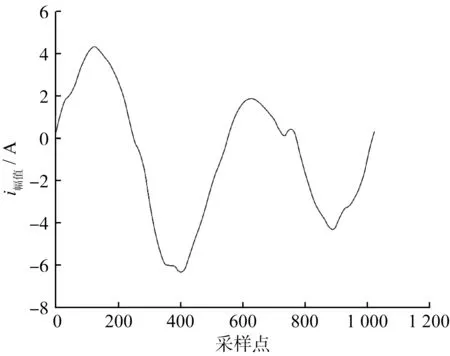
图3 新阈值法降噪
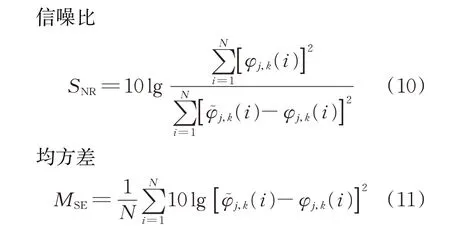
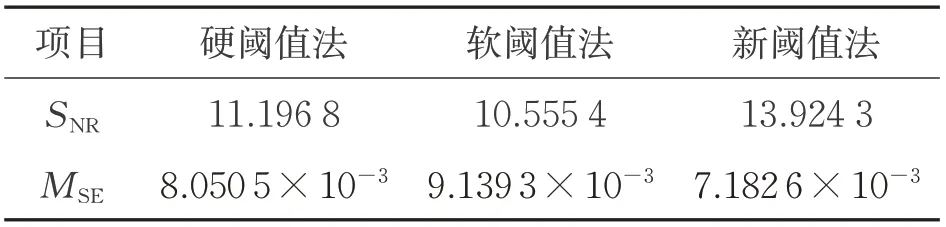
表1 3种阈值降噪法S NR和M SE比较
3 故障类型判别分析
故障类型通常分为固定偏差、精度失真、失效3个突变性故障,变比增大、变比减小、漂移偏差3个渐变性故障。在解决噪声干扰后,将分形维数作为故障信号特征参数,用来判断故障类型。依据故障类型特点,建立输出波形数学模型计算后续盒维数,其中失效故障模型为常数,其他数学模型如下:

式中:A为电压幅值;ω为角频率;φ为相位角;a、c为常数;d为故障比例;t、t0为任意时刻和起始时刻;N(0,σ2)为正态分布,σ2为方差。
以A、φ、ω为影响盒维数的故障因素,依次选取一个故障因素变化,其他恒定,基于输出波形模型,通过网格维数Db计算得到故障波形A变化的盒维数(见表2)、故障波形φ变化的盒维数(见表3)和故障波形ω变化的盒维数(见表4)。
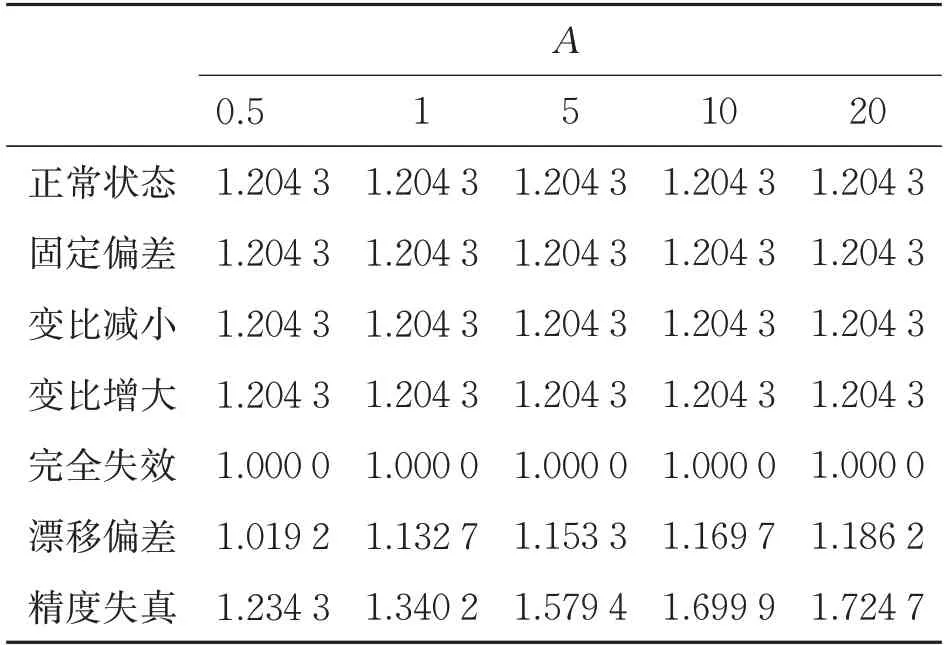
表2 故障波形A变化的盒维数
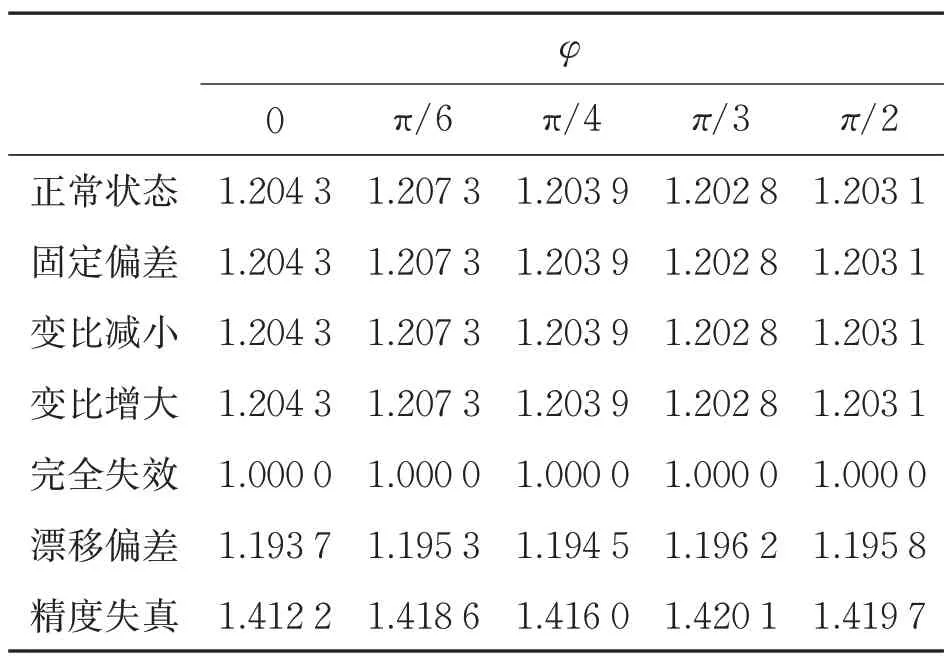
表3 故障波形φ变化的盒维数
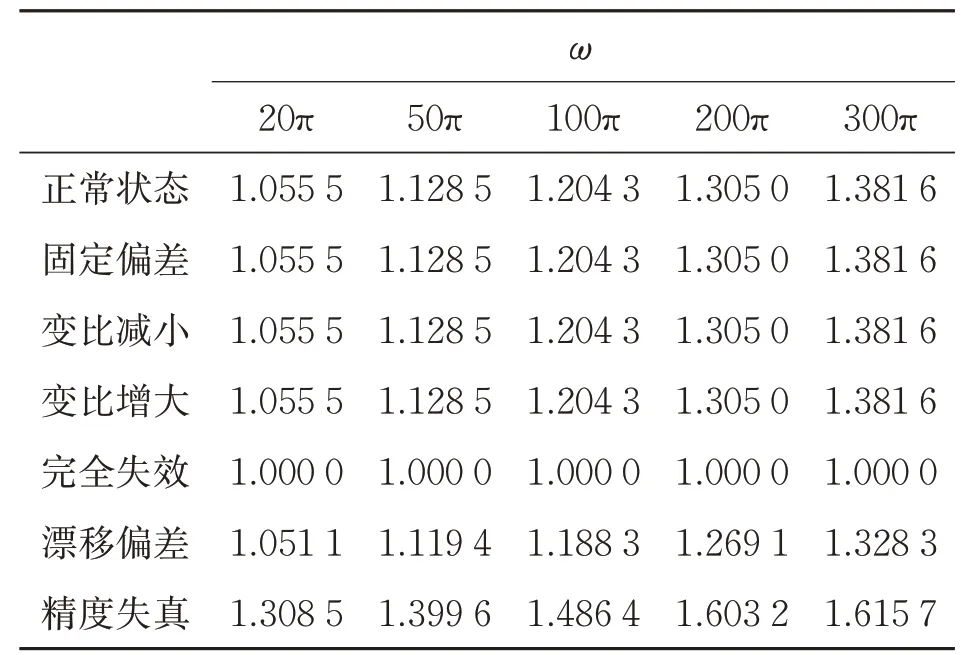
表4 故障波形ω变化的盒维数
为表述方便,将故障盒维数定义为Df,正常状态盒维数定义为Dn。分析盒维数变化情况,失效故障波形通常表现为直线,所以Df恒为1;精度失真、漂移偏差Df和正常状态有恒定大小关系,依据大小关系可直接判断。固定偏差、变比增减故障Df与正常状态Dn相等,A也相等,但固定偏差波形极大值A+与极小值A-之和不为零;变比增减故障波形两个极值相加为零,极大值与A却存在大小关系,所以固定偏差和变比增减故障可从极值和幅值大小判别故障类型。归纳的故障类型判别参考如表5所示。

表5 故障类型
以故障状态Df和正常状态Dn为主要关系,幅值和极值为辅助关系,归纳出表5作为故障类型判断的依据,方便直观且有很好的准确性。实验结果表明,以盒维数为主要特征值结合幅值和极值的方法,可有效判断剩余电流互感器故障的类型,保障智能漏电保护器的正常运行,预防漏电事故发生。
4 结 语
通过分形理论对剩余电流互感器故障进行分析,以单重分形盒维数为基础的网格维数很好地将分形理论应用于剩余电流输出波形盒维数计算,同时用新小波阈值降噪法解决了输出波形的非连续性和偏差问题。对剩余电流输出波形建立数学模型,以盒维数和极值、幅值的比较可以准确判断剩余电流互感器故障类型。针对剩余电流互感器故障问题,该方法能够及时定位故障,并快速精确判断出故障类型,避免漏电事故发生。
