基于预测误差校正的宽度学习短期风电功率预测
2021-09-01文传博
赵 阳,文传博
(上海电机学院电气学院,上海201306)
风能是一种具有低成本、清洁、可再生的能源。风力发电作为一种成熟技术得到广泛应用[1]。风电功率的随机性易造成电网波动,干扰电力系统调度。因此,通过短期风电功率的准确预测改善风电功率的模糊程度,有利于风电能源的合理开发与利用,使电网系统稳定运行[2]。目前,风功率预测按不同的模型分为[3]:物理模型[4]、统计模型[5]、元启发式模型[6]和组合模型[7]。
由于风电功率的不确定性,单一的预测方法不能够对复杂的风电功率数据样本进行准确地预测。为了减小风电功率的随机波动性,将风电功率序列分解为一系列的子信号进行预测,再将各子信号的预测值进行重构,提高了风电功率的预测准确性。王俊等[8]基于变分模态分解(Variational Modal Decomposition,VMD)与长短时记忆网络(Long and Short Time Memory Network,LSTM)的预测方法,VMD能够有效地克服信号混叠现象,提高组合预测方法的准确性。李霄等[9]提出改进最小二乘支持向量机(Least Squares Support Vector Machines,LSSVM)和预测误差校正的预测方法,对预测误差校正,提高预测精度。周楠等[10]基于宽度学习(Broad Learning System,BLS)算法通过对特征层和增强层的扩展来提高网络性能,但特征节点、增强节点的个数会影响预测精度。通过麻雀搜索算法对BLS的参数进行寻优能够避免陷入局部最优问题,得到更高性能的BLS模型。
本文提出基于预测误差校正的BLS短期风电功率预测方法。考虑到预测误差序列对预测带来的影响,通过变分模态分解与麻雀算法优化宽度学 习(Variational Mode Decomposition and Sparrow Algorithm Optimized Broad Learning System,VMD-SSA-BLS)模型对误差进行分解预测,使短期风电功率的预测准确性得到提高,并采用沿海某风电场的实测数据进行仿真验证。
1 建模原理
1.1 VMD
VMD是一种自适应和非递归的分解方法[11]。主要思想是通过构造变分问题进行迭代求解。通过提前设置好的模态数K将非平稳信号f(t)分解出不同中心频率和带宽的子信号u(k),更新各模态函数及其中心频率,当各模态的估计带宽之和最小时结束更新得出最优解。过程如下[12]:
(1)通过Hilbert变换计算各模态分量的单边频谱,并估计出相应的中心频率ωk。
(2)将各模态解析信号中心频率的指数项e-jωkt进行混叠,并将各模态的频谱转换到对应的基频带。
(3)由高斯平滑法对各模态的带宽大小进行预算,转化为带约束条件的变分求解问题:
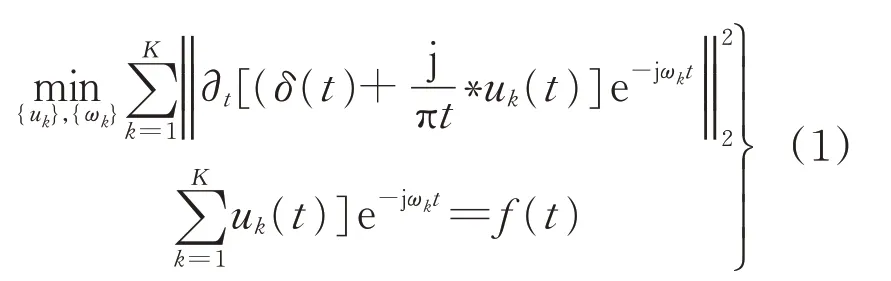
式中:δ(t)为单位脉冲函数;*表示卷积;∂(t)表示偏导;uk(t)为第k个分量;ωk为k个分量的中心频率;f(t)为风电功率的时间数据。
对式(1)中的约束问题引入拉格朗日乘子λ和惩罚因子α,将其变为非约束的变分问题:

利用交替方向乘子法(ADMM)求解式(2)中的鞍点,更新相应变量uk、ωk、λ为
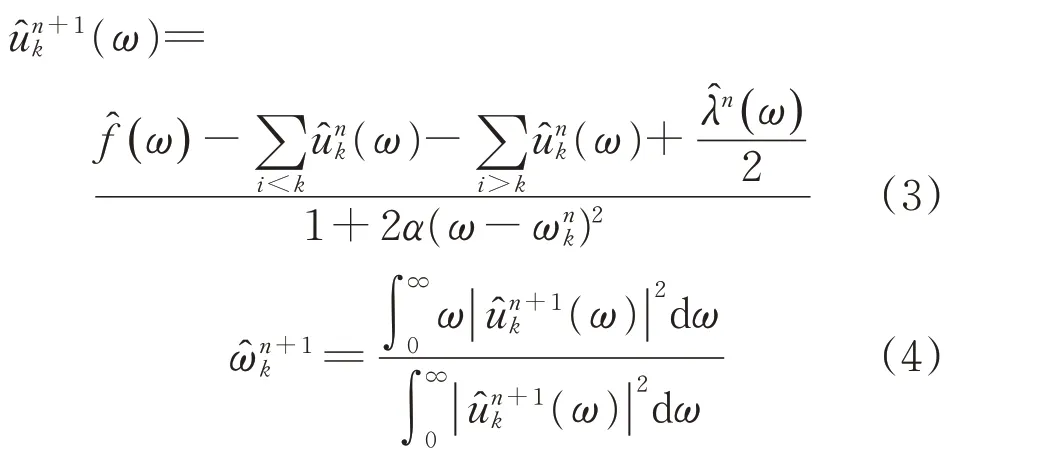
式中:n为迭代次数。
综上可得,VMD的步骤如下:
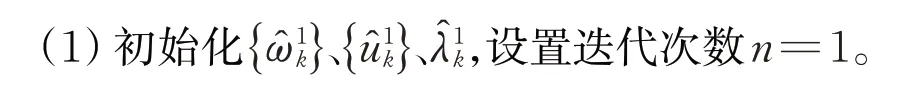
(3)根据下式对拉格朗日乘子进行更新:
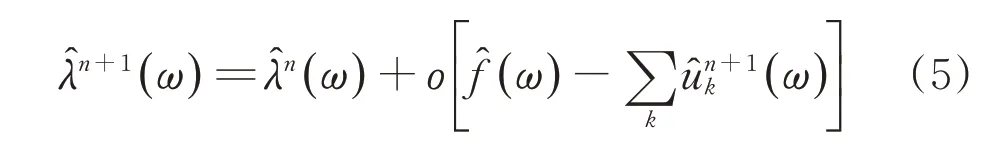
式中:ο为更新因子。
(4)判断下式的收敛条件是否满足要求
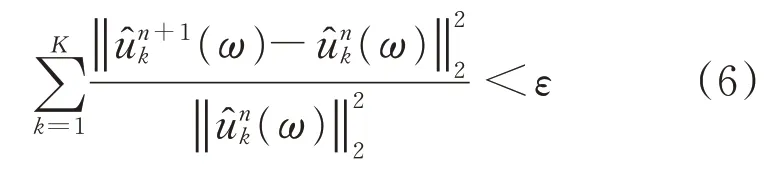
式中:ε为判别精度。若满足则停止分解;否则对迭代次数n进行加1,并返回步骤2。
1.2 麻雀搜索算法
麻雀搜索算法(Sparrow Search Algorithm,SSA)由薛建凯等[13]于2020年提出。SSA对种群内部进行明确的分工,一部分麻雀作为发现者(10%~20%)进行寻食,为加入者的觅食范围和方向提供参考。剩余麻雀作为加入者从发现者上获食,发现者和加入者之间可以互换,但比例保持恒定。随机选取发现者和加入者中的麻雀(10%~20%)作为侦察者进行监视,当有麻雀意识到危险,会及时发出警报信号,整个种群会立刻做出反捕食行为。
发现者位置更新如下:
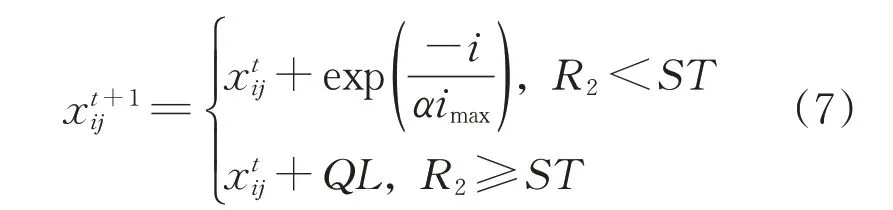
式中:imax为算法的最大迭代次数;α为(0,1]之间的随机数;R2∈[0,1]、ST∈[0.5,1]为预警值和安全阈值;Q为随机数且服从正态分布;L为1×d且元素为1的矩阵,d为麻雀维数。
加入者位置更新如下:

侦察者位置更新如下:
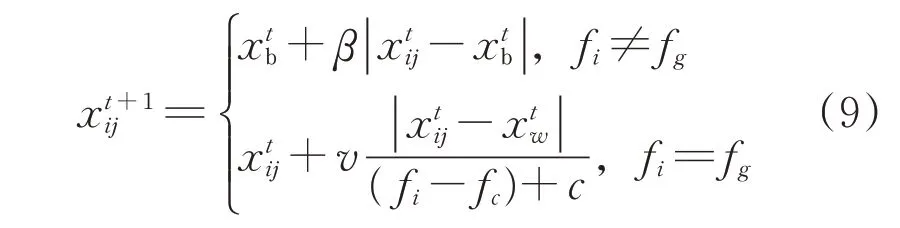
式中:为第t次迭代时的全局最佳位置;β为服从正态分布的随机数,以控制步长;v为[-1,1]的随机数;fi、fg和fw分别为当前麻雀的适应度、全局最优和最差适应度;c为常数以避免除数为零。
SSA基本流程:
(1)种群初始化;
(2)计算麻雀种群个体适应度函数,求出当前最佳位置、最差位置和最差适应度;
(3)根据式(7)~(9)对发现者、加入者和侦察者位置进行更新;
(4)对适应度进行更新;
(5)若达到最大迭代次数,算法停止寻优,否则返回步骤3。
1.3 BLS
BLS系统是由Chen等[14]提出的一种新型神经网络。BLS一共有3层,分别为映射层、强化层和输出层。数据经过映射层生成特征节点,之后特征节点通过强化层生成增强节点,特征节点和增强节点均与输出层直接连接,如图1所示。
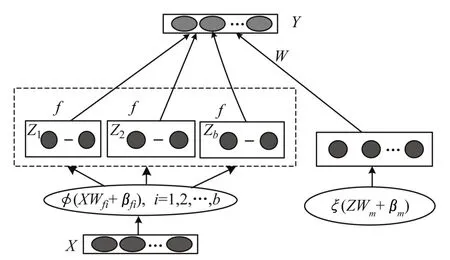
图1 BLS网络
在网络中共有b组特征节点,每组包含f个节点,m个增强节点。对样本X进行特征映射:
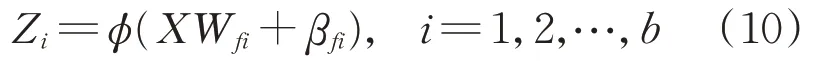
式中:Wfi、βfi为[-1,1]的随机数;ϕ(⋅)为一个映射函数。所有特征节点可以表示为:Z=[Z1,Z2⋅⋅⋅,Zb],那么增强节点可以表示为
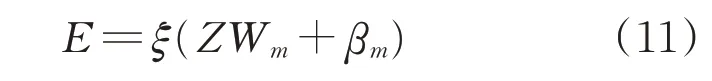
式中:Wm、βm为[-1,1]的随机数;ξ(⋅)为激活函数。
因此,宽度学习网络输出模型可以表示为

式中:H=[Z|E];W为将特征节点和增强节点连接到输出层的输出权重。
在训练过程中,Wfi、Wm、βfi和βm的值均不发生改变,又已知Y和H的值,故只需对W进行求解,即

式中:H+为广义逆矩阵。
BLS训练步骤如下:
(1)对数据划分为训练集Xtrain、Ytrain,验证集Xtext、Ytext;
(2)根据式(10)、(11)计算Xtrain的特征节点和增强节点,得到中间层训练矩阵Htrain;
(3)根据式(13)计算BLS的输出权重W=
(4)计算Xtext的特征节点与增强节点,得到中间层验证矩阵Htext;
(5)根据Ytext=HtextW得到预测值。
2 基于VMD-SSA-BLS误差校正的建模预测
2.1 SSA优化BLS
为了提高模型的鲁棒性,采用SSA对BLS模型中的特征层b、特征节点f、增强节点m进行寻优,采用平均绝对百分比误差作为SSA算法的适应度函数。
SSA-BLS具体算法步骤如下:
(1)初始化SSA算法中的参数。参数为麻雀种群规模P,麻雀算法的迭代次数imax,发现者个数p,侦察者个数s,最优适应度值F等。
(2)初始化种群。种群维度设定为3维,分别代表BLS的参数特征层b、特征节点f、增强节点m。
(3)根据平均绝对百分比误差计算种群中所有麻雀的适应度值,得到当前最佳适应度的麻雀个体。
(4)执行SSA算法。
(5)判断迭代次数或精度是否达到设置的要求,满足则得出最优值,否则返回到步骤3。
(6)得到最优值,将优化的参数用于建立SSA-BLS的预测模型。
2.2 VMD-SSA-BLS误差校正模型
对风电功率进行预测时,由于风电功率序列的随机性、非线性等特点,对预测效果产生很大的影响,单一的预测模型无法对风电功率进行精准的预测。本文通过BLS作为基础模型对风电功率进行预测,将训练误差和预测误差组成误差序列作为样本;对误差序列进行VMD分解,对分解后的各子模态分别建立SSA-BLS回归预测模型进行误差预测;将各子模态误差预测值叠加求和补偿给功率预测值,得到最终的风电功率预测值,如图2所示。
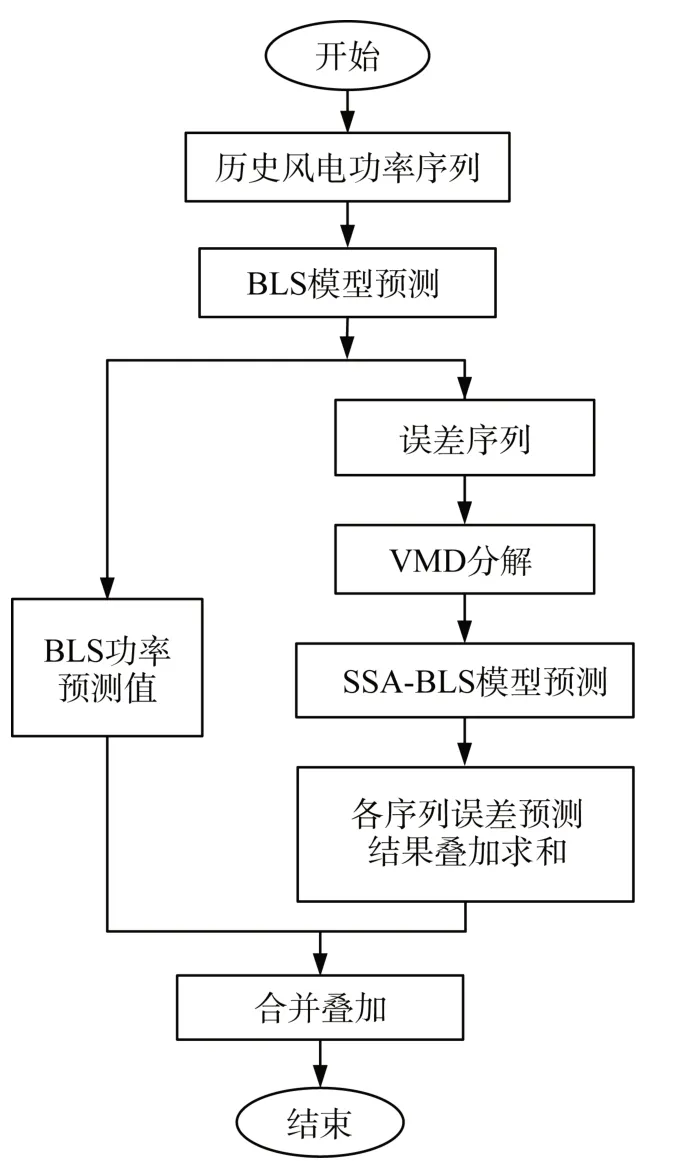
图2 VMD-SSA-BLS模型的预测流程
3 实例分析
3.1 数据分析与处理
为了验证本文所提算法的有效性,选取沿海某风电场2012年7月份的实际采集数据为研究对象,容量为16 MW,采样间隔为1 h。共将768组样本数据通过VMD-SSA-BLS误差校正模型进行分析和预测,输入特征选为风电功率之前的数据,根据相关度分析,选取前8个时刻的数据作为输入特征向量,前672组数据作为训练数据,后96组数据作为测试数据。
对原始风电功率时间序列归一化处理后进行BLS模型预测,产生的误差序列进行VMD分解,分解时需要确定模态数K的值。K值选择过大会造成信号特征分量过分解,K值选择过小又会造成信号特征分量欠分解,导致各分量模态混叠,无法准确提取信号中包含的特征分量。K的确定需判断VMD分解的最后一个模态分量与风电功率序列的相关系数是否小于5%[15],因此本文选取参数K=6、α=800,VMD分解结果如图3所示。
通过SSA优化后的BLS网络对图3中VMD分解的分量进行预测。在SSA参数中,种群规模为20,迭代次数为50次,发现者个数为14,侦察者个数为6。在BLS中,增强节点的激活函数为‘tansig’,参数特征节点f和特征层b设置为[1,50],增强节点m范围设置为[1,1 000]。通过SSA优化后的BLS网络对各分量误差预测结果如图4所示。

图3 VMD分解
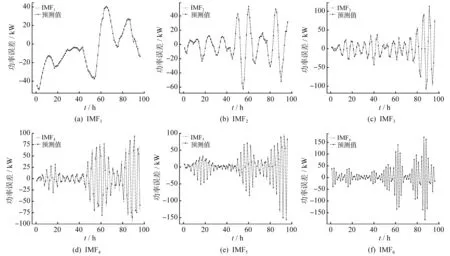
图4 各分量误差预测曲线
从图4可以看出,对VMD分解后的各分量进行SSA-BLS建模并预测的曲线拟合度高。表明SSA-BLS模型预测较好,VMD分解可以很好地去除误差的部分噪声,使误差序列变得更平滑。对各分量预测误差叠加结果如图5所示。
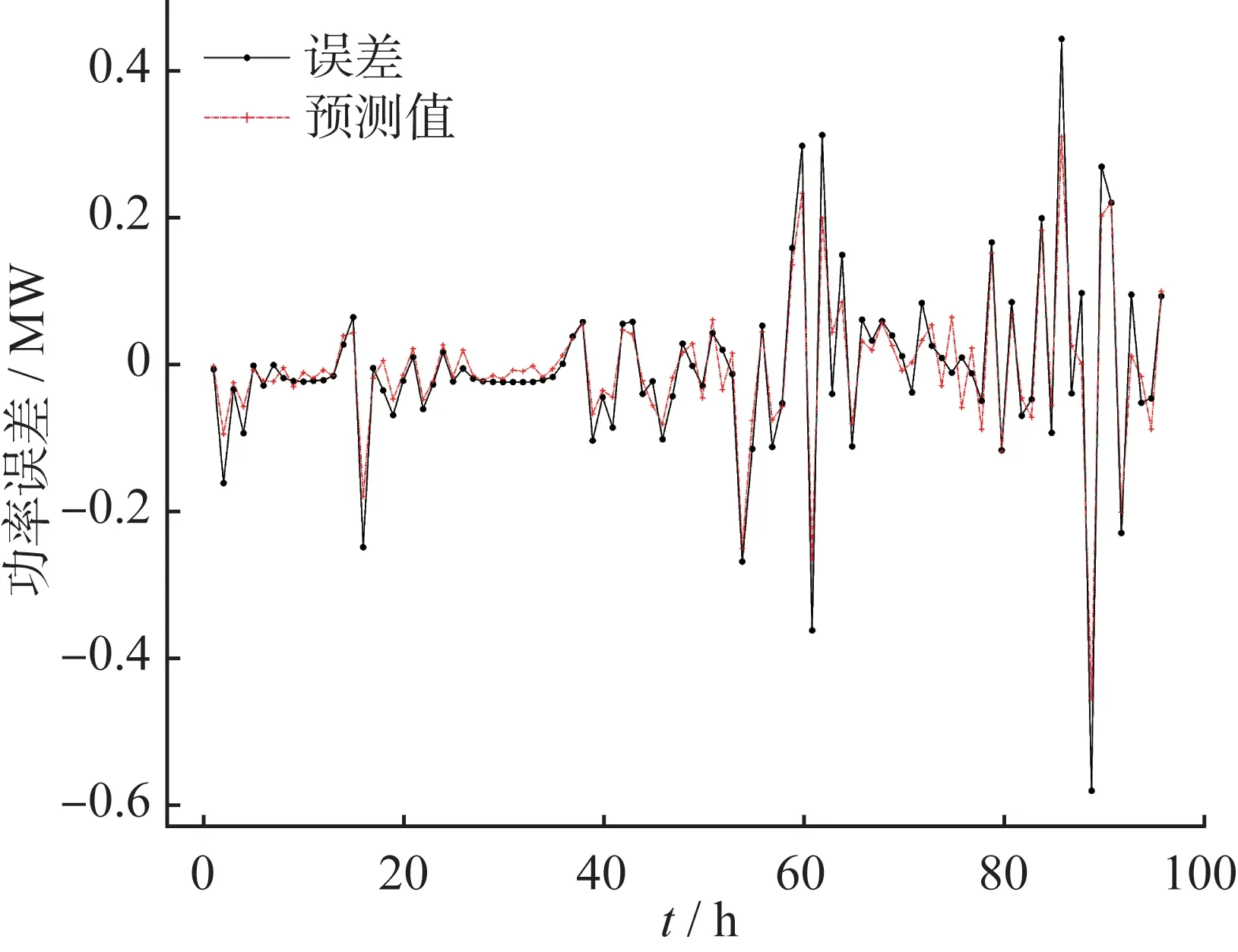
图5 误差预测曲线
从图5可以看出,VMD-SSA-BLS模型对误差预测最终结果中,误差预测结果的拟合度非常高,尤其是在误差的极点处重合度较高。因此,通过VMD-SSA-BLS模型对误差进行处理后,预测效果非常明显。
3.2 结果分析
建立BLS、SSA-BLS、经验模态分解与麻雀算法宽度学习(EMD-SSA-BLS)、集合经验模态分解与麻雀算法宽度学习(EEMD-SSA-BLS)、VMDSSA-BLS等5种模型来更好地对预测结果进行对比。评价指标选取均方根误差(RMSE)、相对百分误差绝对平均值(MAPE)和绝对平均误差(MAE)。
各模型预测结果如图6所示,预测误差指标如表1所示。
为验证组合模型预测的有效性及精度,将VMD-SSA-BLS与BLS、SSA-BLS、EMD-SSABLS、EEMD-SSA-BLS等预测模型的预测结果分别与实际值进行比较。由图6可知,经SSA优化后的BLS模型预测结果要优于单一模型BLS;通过EMD、EEMD和VMD分解方法对非线性、非平稳性的风电功率误差序列进行处理之后再预测的曲线拟合效果中,VMD对风电功率误差序列的分解效果要优于EMD、EEMD。由表1可知,本文提出的VMD-SSA-BLS模型对风电功率预测的结果评价指标MAE、RMSE、MAPE值均小于BLS、SSABLS、EMD-SSA-BLS、EEMD-SSA-BLS等4种模型。VMD-SSA-BLS模型各项指标综合表现最优,因此本文的预测方法与传统预测方法相比,在一定程度上提高了预测模型的准确性。
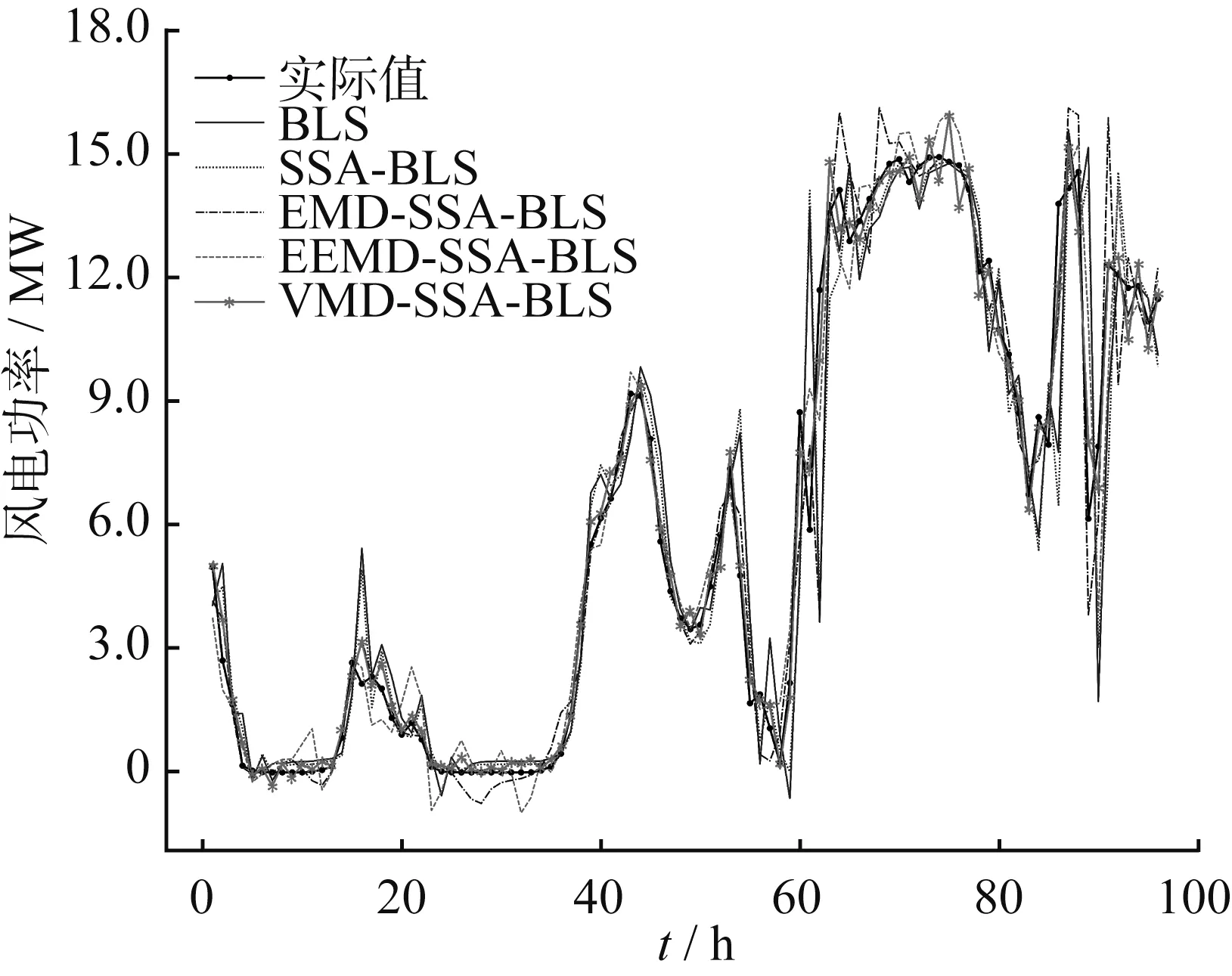
图6 各模型预测曲线
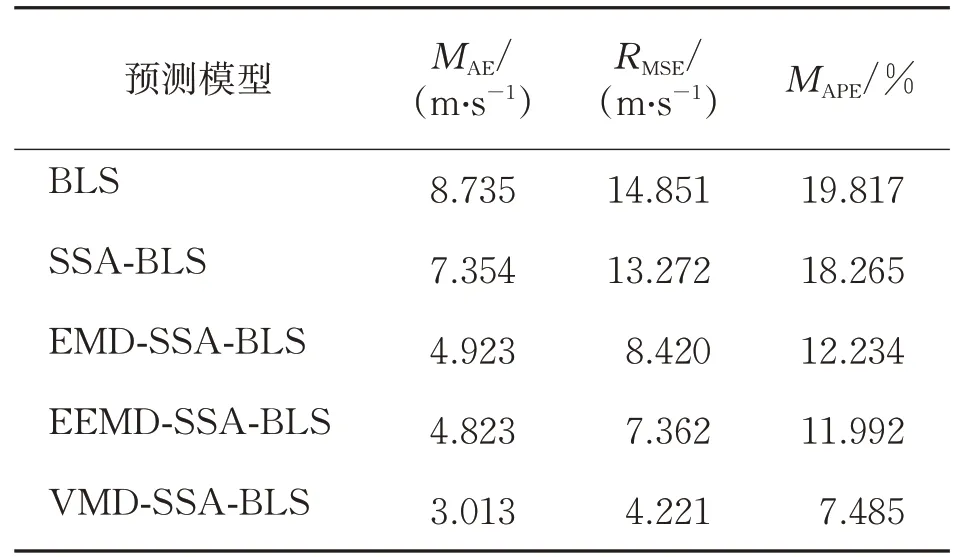
表1 各模型预测误差指标
4 结 论
针对风电功率短期预测,提出了一种基于VMD-SSA-BLS的误差校正组合预测模型,通过实际风电场的运行数据进行验证,得出以下结论:
(1)通过沿海某风电场的实测数据进行仿真验 证,并 与BLS、SSA-BLS、EMD-SSA-BLS、EEMD-SSA-BLS等模型进行比较。结果表明,VMD-SSA-BLS算法模型的预测效果更好。
(2)采用SSA优化BLS的参数能够提高模型泛化能力和预测准确性。
(3)在预测误差校正时,考虑到风电功率序列预测误差的非平稳性,采用对误差序列进行VMDSSA-BLS模型预测的效果优于直接对误差预测的传统模型效果。
