飞行员跳伞模拟训练系统人伞惯性参数研究
2021-09-01周晓光张源原
周晓光,朱 鹏,张源原,路 欢,周 媛
(海军航空大学,辽宁葫芦岛 125000)
跳伞是飞行员必须具备的救生技能,以应对在作战和训练中突遇险情。各种基于VR虚拟技术的跳伞模拟器发展迅速,为飞行员跳伞训练提供了新的方法和途径。基于VR 的跳伞模拟器研制,首先要解决伞降过程动力学仿真问题。在实物载荷的降落伞动力学建模方面,国内外都做了大量的研究工作。此类研究中,均假定载荷为简单的圆柱体或者方体,与实际跳伞员参数有较大区别。为进一步提高飞行跳伞模拟训练系统动力学仿真参数准确性和系统逼真度,本文对飞行员跳伞模拟训练系统的人伞惯性参数计算方法展开研究。
降落伞开伞后,运动过程分为自由坠落、拉直、充满和稳定下降4 个阶段,一般采用分段简化的方法进行动力学建模。本文以稳定下降阶段人伞系统的惯性参数为例,人伞系统如图1 所示。降落伞为环形训练伞,主要由伞衣、伞绳、操纵带、操纵绳、伞包背带系统等组成。训练人员须着作训服、作训靴,两臂上举,两腿自然下垂。

图1 人伞系统Fig.1 Human-parachute system
为描述人伞系统,构建人伞系统体固定坐标系O
-xyz
,如图2所示。坐标系O
-xyz
的原点O
在伞衣开口平面的伞衣基准平面中心原点,x
轴和y
轴在伞衣基准平面内,z
轴指向载荷人。各主要参考点与参考面的距离如图2 所示,z
、z
、z
、z
、z
分别为参考面到伞衣质心、伞绳质心、人体质心、降落伞压心和人伞系统质心的距离。
图2 人伞基本结构Fig.2 Basic structure of human-parachute system
1 降落伞惯性参数
1.1 伞衣惯性参数
降落伞伞衣可以简化为半径R
,质量为m
球壳,如图3所示。则其绕球心3个轴的转动惯量计算公式为:
图3 伞衣Fig.3 Parachute canopy
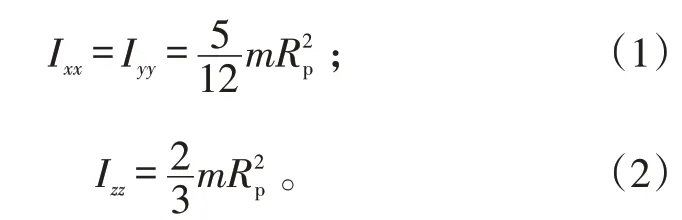
1.2 伞绳惯性参数
伞绳和操控带组成一个锥形圆台壳体,如图4 所示。其中,锥形圆台上截面半径为R
,下截面半径为R
,质量为m
。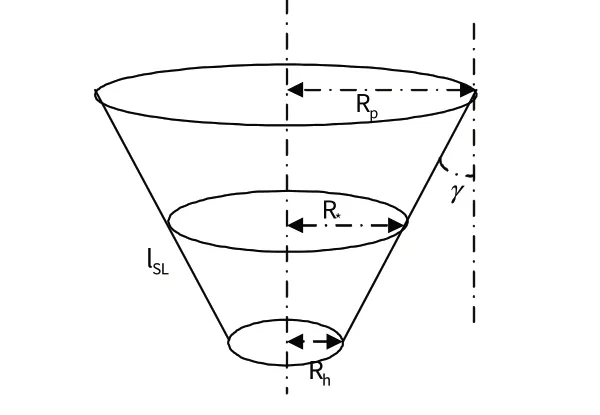
图4 伞绳及操控驱动系统Fig.4 Parachute lines and control system
锥形圆台壳体的转动惯量计算公式如下:
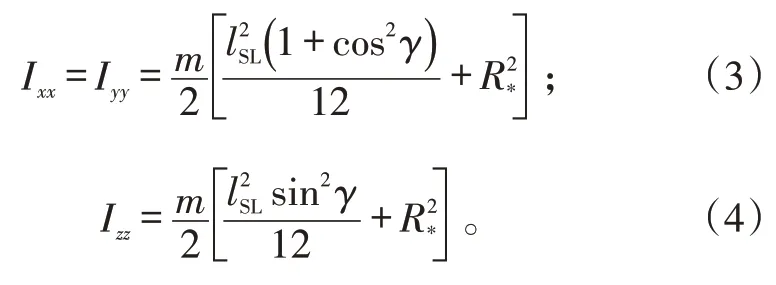
m
为圆台壳体质量;l
为侧外边长;γ
为圆锥半角;R
为z
轴方向质心处圆台半径,R
=R
-l
sinγ
/2,R
为伞衣半径;l
为伞绳和操纵带长度。2 人体惯性参数
人体简化模型采用Hanavan人体数学模型,主要由15部分组成,如图5所示。其中,1为头、2为上躯干、3为下躯干、4为右手、5为左手、6为右上臂、7为左上臂、8为右前臂、9为左前臂、10为右大腿、11为左大腿、12 为右小腿、13 为左小腿、14 为右足、15 为左足。其中,1、4、5为椭球,2、3为椭圆柱,其余为原锥台。人体坐标系原点在人头顶,X
轴指向前方,Y
轴指向右侧,Z
轴指向下方。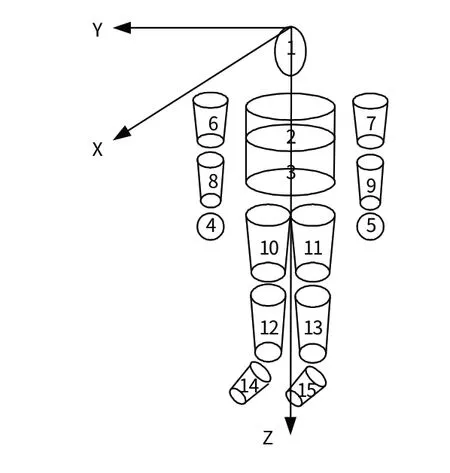
图5 人体简化模型Fig.5 Simplified human model
2.1 人体模型各环节重量分配
Hanavan 人体模型各关节的质量分配采用Barter的回归方程:

2.2 各环节惯性参数计算
假定踝围为C
、腋下臂围为C
、臀后为D
、胸宽为B
、胸厚为D
、肘围为C
、拳围为C
、前臂长为L
、足长为L
、膝围为C
、头围为C
、臂宽为B
、臂高为H
、坐高为H
、内踝高为H
、身高为H
、胸骨下沿高为H
、大腿围为C
、胫骨高为H
、转子高为H
、上臂长为L
、体重为W
、腰宽为B
、腰厚为D
、腕围为C
。2.2.1 头
头的模型是一个正椭圆球,椭球的长半轴为R
,短半轴为R
,环节长为S
,质心为CG
,重心位置比例系数为η
,环节质量为S
,环节密度为δ
。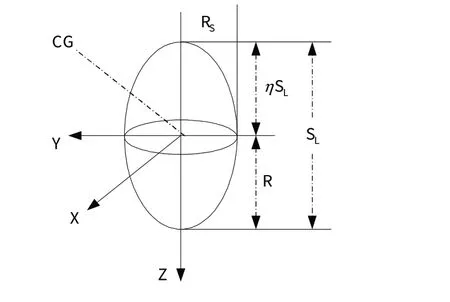
图6 头的简化模型Fig.6 Simplified head model
头环节的惯性参数计算如下,其中用I,I,I
分别表示Hanavan 人体数学模型15 个组成部分绕x,y,z
轴的转动惯量:
2.2.2 上躯干
上躯干模型为正椭圆柱,与xy
平面平行的截面是椭圆,如图7所示。
图7 上、下躯干简化模型Fig.7 Simplified trunk model
上躯干惯性参数计算如下:
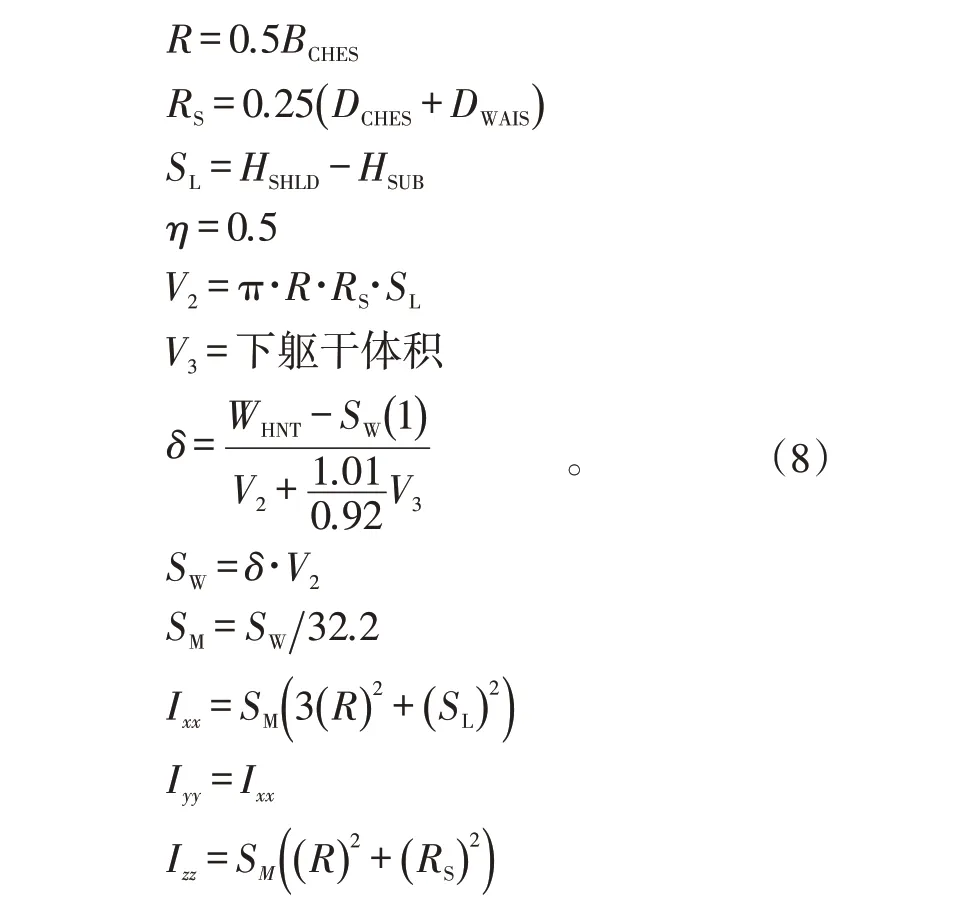
2.2.3 下躯干
下躯干的模型是正椭圆柱,与xy
平面平行的截面是椭圆,如图7所示。下躯干惯性参数计算如下: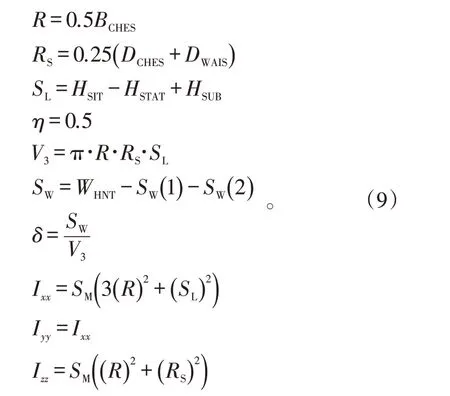
2.2.4 手
手的模型是球体,几何参数和铰点位置如图8 所示。
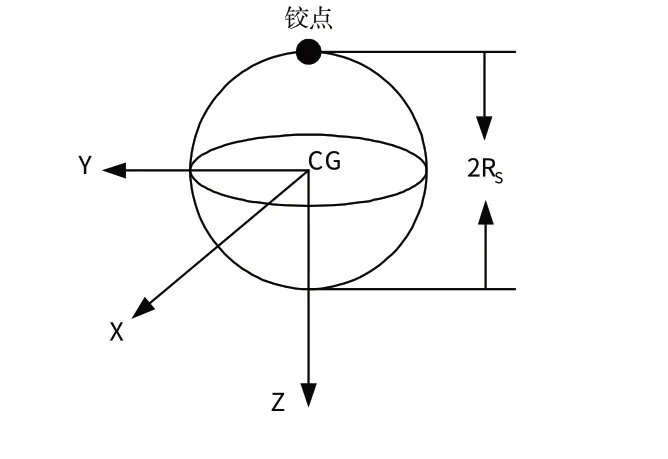
图8 手的简化模型Fig.8 Simplified hand model
手的惯性参数计算如下:
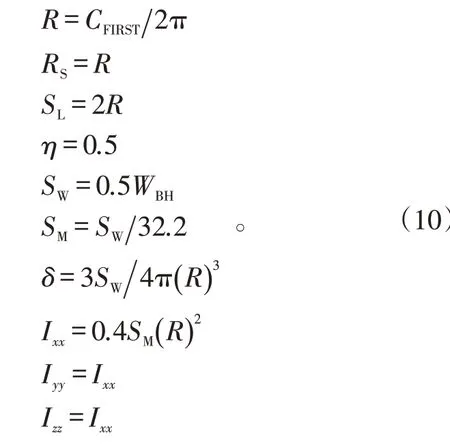
2.2.5 上臂
上臂模型是平截头正圆锥体,与XY
平面平行的是圆,几何参数和铰点位置,如图9所示。
图9 上臂模型Fig.9 Simplified upper arm model
上臂的几何参数和质量如下:

2.2.6 前臂
臂模型是平截头正圆锥体,与XY
平面平行的是圆,几何参数和铰点位置,如图10所示。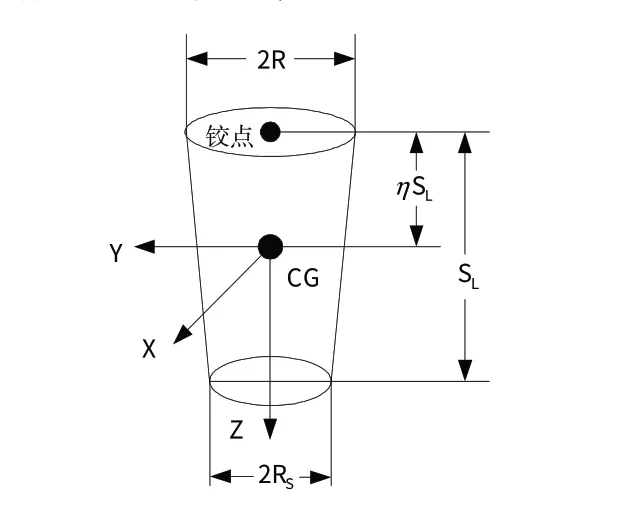
图10 前臂模型Fig.10 Simplified forearm model
几何尺寸和质量计算如下:
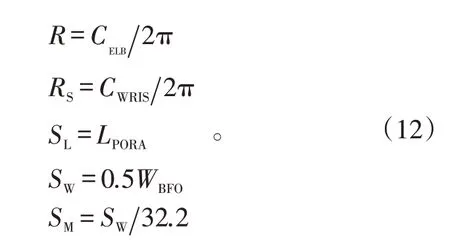
2.2.7 大腿
大腿模型是平截头正圆锥体,与XY
平面平行的是圆,几何参数和铰点位置如图11所示。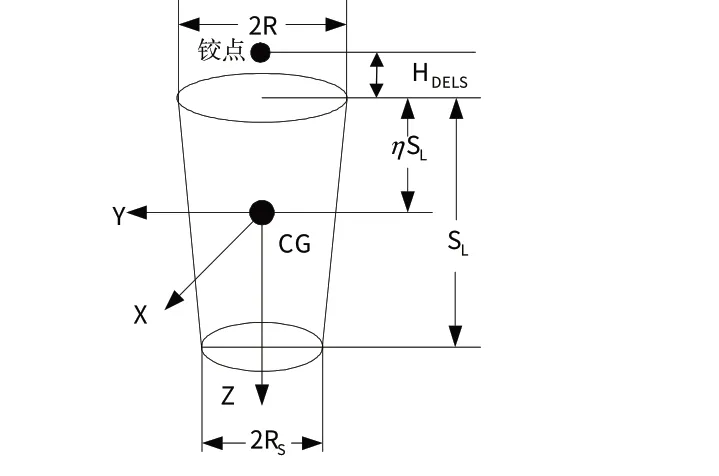
图11 大腿模型Fig.11 Simplified thigh model

2.2.8 小腿
小腿的模型是平截头正圆锥体,与XY
平面平行的是圆,几何参数和铰点位置,如图12所示。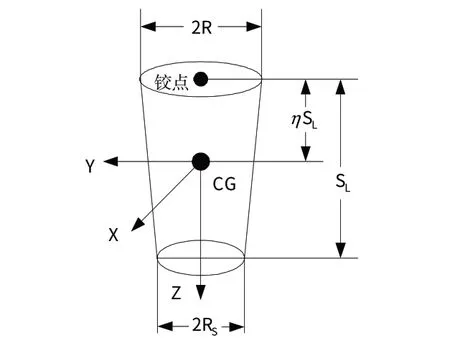
图12 小腿模型Fig.12 Simplified shank model
几何尺寸和质量计算如下:
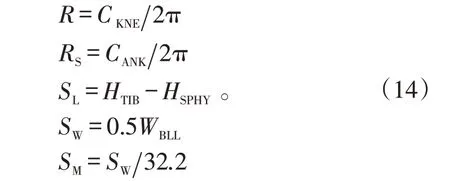
2.2.9 足
足的模型是平截头正圆锥体,与XY
平面平行的是圆,几何参数和铰点位置如图12所示。几何参数和质量计算如下:

人体环节6~15(锥台)具有共同性质,转动惯量计算如下:
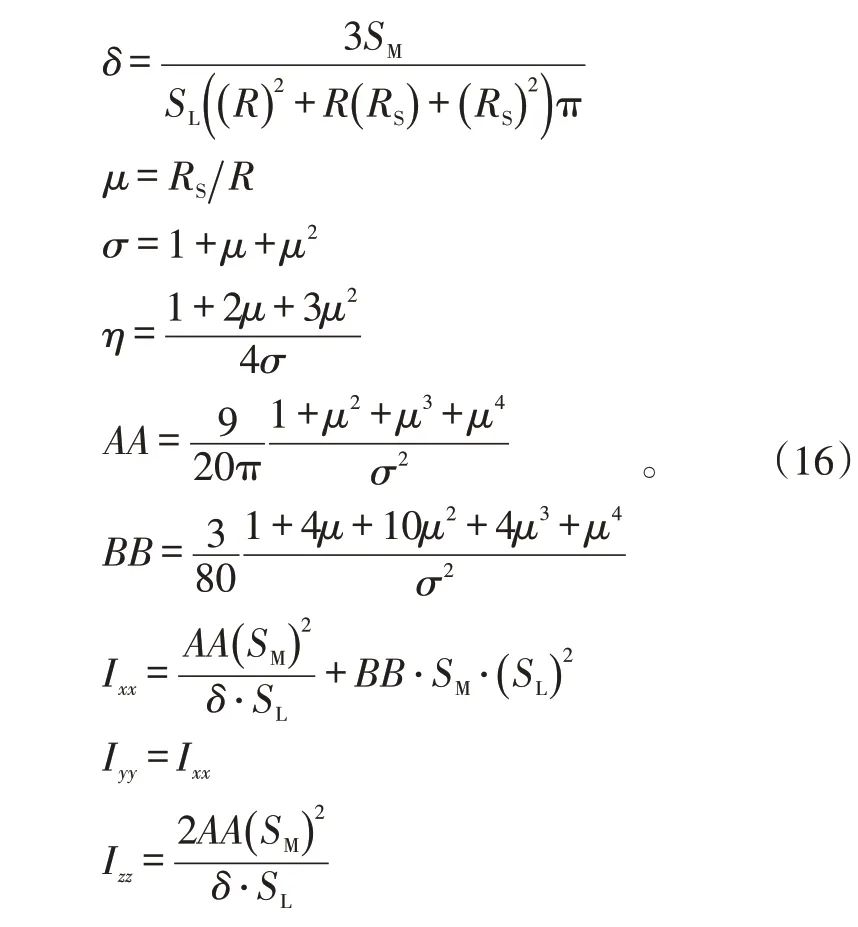
2.3 人体模型转动惯量合
为描述身体各部分的位置,引入欧拉角仰角θ
和偏角θ
如图13所示。用于描述身体各部分的空间姿态,该坐标系的原点位于身体环节的质心,欧拉角的参考坐标系是躯干。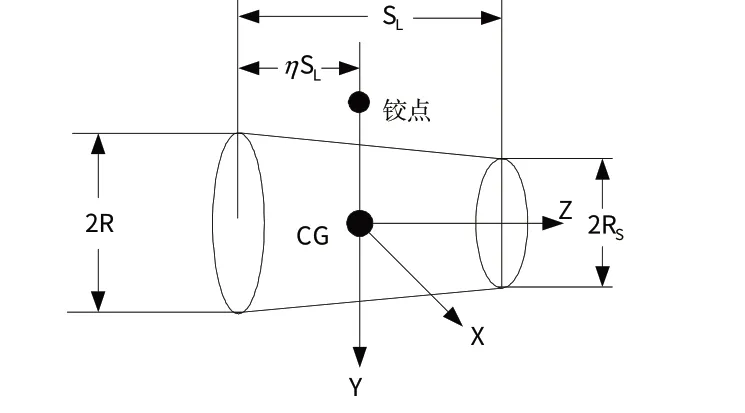
图13 足模型Fig.13 Simplified foot model
人体环节i
根据欧拉角构建转换矩阵A
,根据与质心的距离可以构建张量矩阵B
,那么人体环节i
在人体质心坐标系下的惯性参数为:
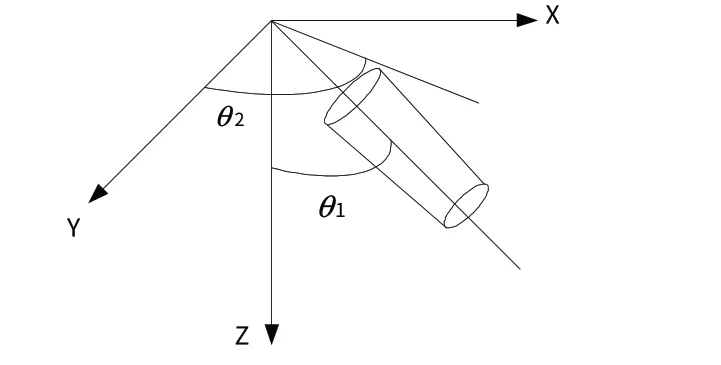
图14 欧拉角Fig.14 Euler angle
3 人伞系统惯性参数
根据以上计算结果,人伞系统各部分惯性参数计算方法,如表1所示。

表1 人伞系统惯性参数计算表Tab.1 Calculation table of inertial parametersof human-parachute system
根据转动惯量平行轴定理,将单独部分的转动惯量转化至体坐标系O
-xyz
下:

4 仿真分析
4.1 参数设定
以某型训练伞为例,伞衣基准面半径R
=3.
34 m,伞衣重量m
=20 kg。伞绳和操控带长度l
=8 m,质量为m
=5 kg。人的质量M
=60 kg,身高H
=1.6 m,人体其他参数按照常规人体给出。4.2 结果分析
人伞系统惯性参数计算结果,如表2所示。

表2 人伞系统惯性参数计算值Tab.2 Calculated value of inertial parameters of human-parachute system
将本文惯性参数计算结果带入文献[8]的人伞运动模型进行仿真验证,设置无风和有风2组仿真条件,仿真中采用的风场模型由某着陆场多年测量数据统计处理得到,其不同高度上的风速、风向数据如表3所示,实际风速值可通过插值获得。
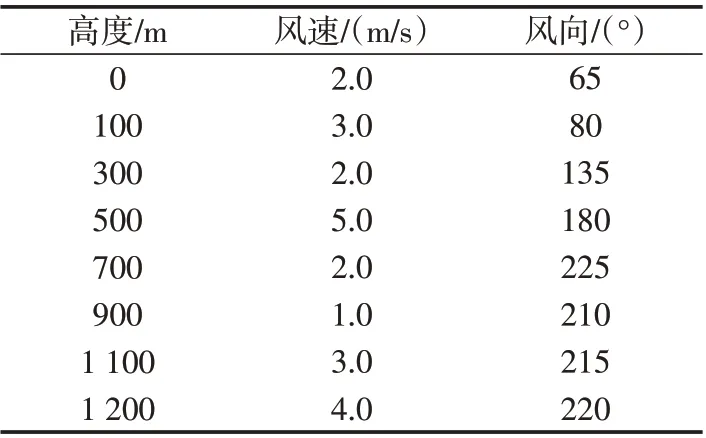
表3 风场数据表Tab.3 Data table of wind field


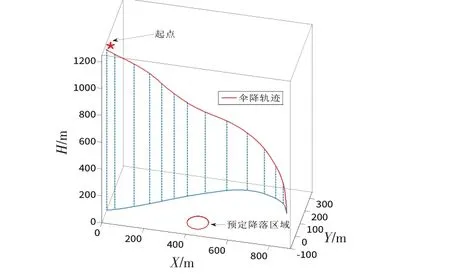
图15 无风伞降三维轨迹图Fig.15 3D trajectory of human-parachute system without wind disturbance
进一步观察图16中的仿真曲线可以发现,在人伞系统稳定下降的初始阶段,由于降落伞气动力的作用,人伞系统出现俯仰角θ
=3.
5°
的前倾,随后在系统重力矩的平衡下迅速恢复平衡状态,即无姿态角的垂直降落,而系统总攻角与迎角快速收敛于20°
,表明本文采用的圆形降落伞为存在平衡攻角的不稳定型伞,与本文中采用某型训练伞的气动规律表现出一致性。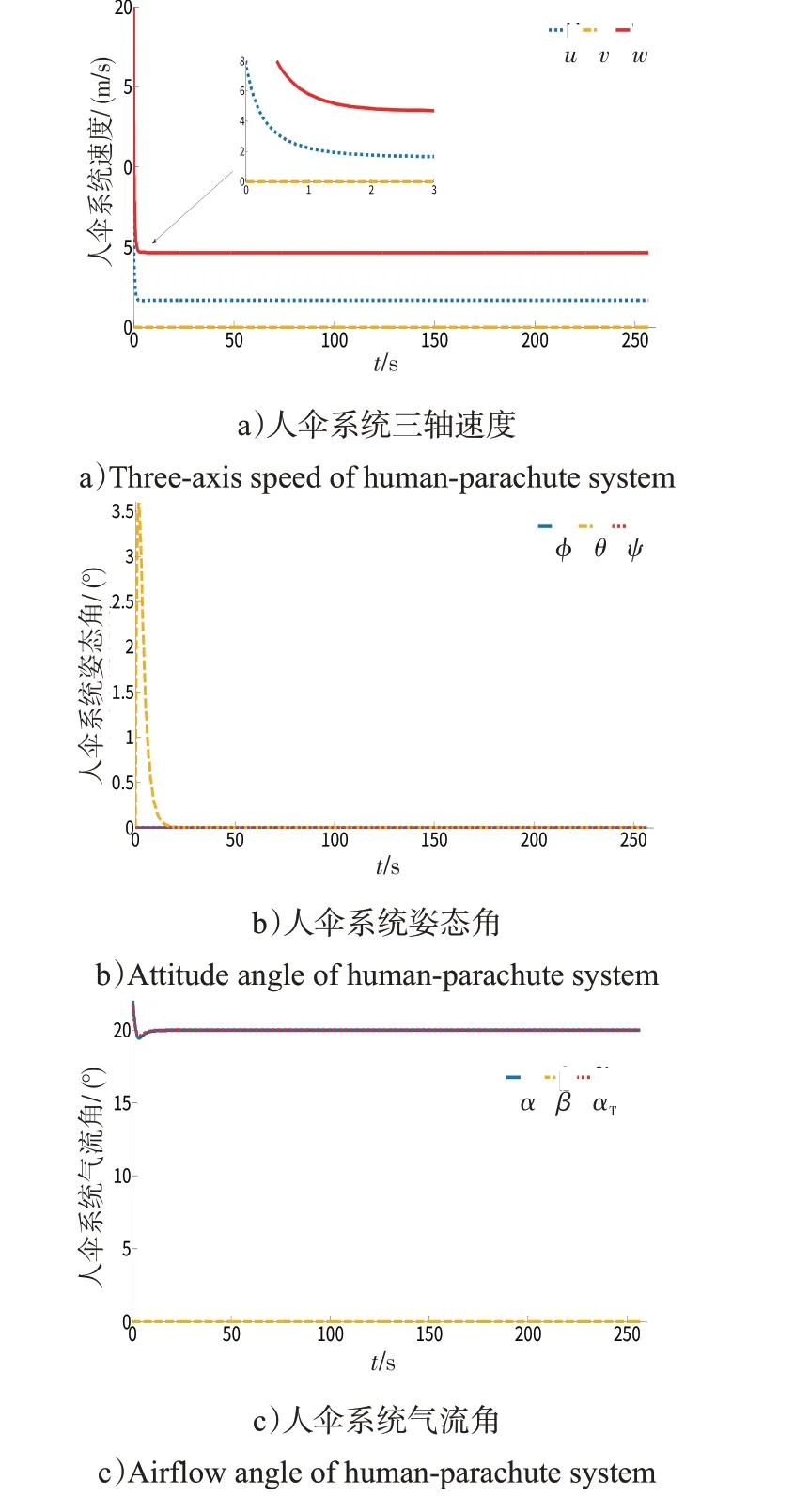
图16 无风情况下的人伞系统参数仿真曲线Fig.16 Simulation curve of parameters of human-parachute system without wind disturbance
由图17、18 可以看到,人伞系统在风场扰动下运动轨迹发生偏移,最终降落点超出了预定降落区域。而分析其速度变化量可以看到,在没有垂直风场的情况下,系统稳定下降速度几乎没有波动,表明水平方向的风场扰动不会影响伞降垂直方向的受力平衡。同时,可以发现,人伞系统三轴速度的变化与风速密切相关,且在气动力达到平衡状态过程中,人伞系统的绝对速度越来越接近风速,即对空相对速度越来越小,使系统运动轨迹的变化基本取决于风速的改变。这表明若能提前获得伞降区域的风场信息,可通过本文模型有效模拟伞降轨迹,提前预测降落区域,甚至通过改变伞降起点以使跳伞员顺利降落至预定区域。
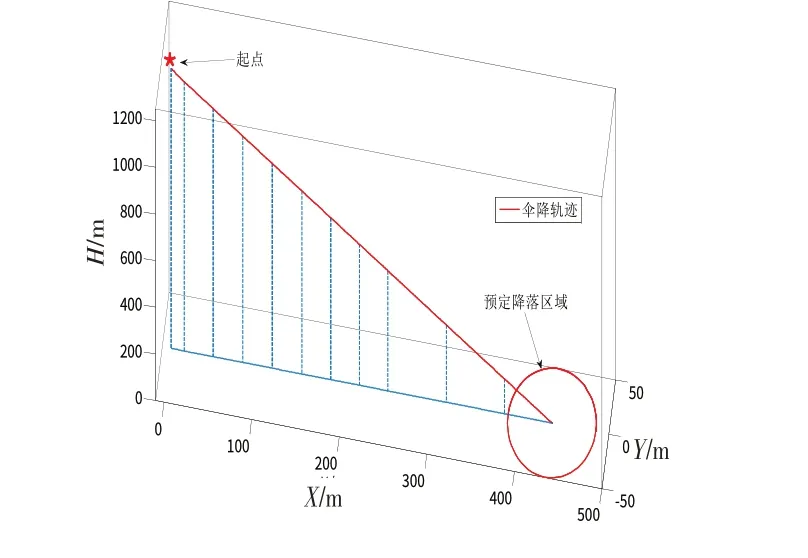
图17 有风伞降三维轨迹图Fig.17 3D trajectory of human-parachute system with wind disturbance
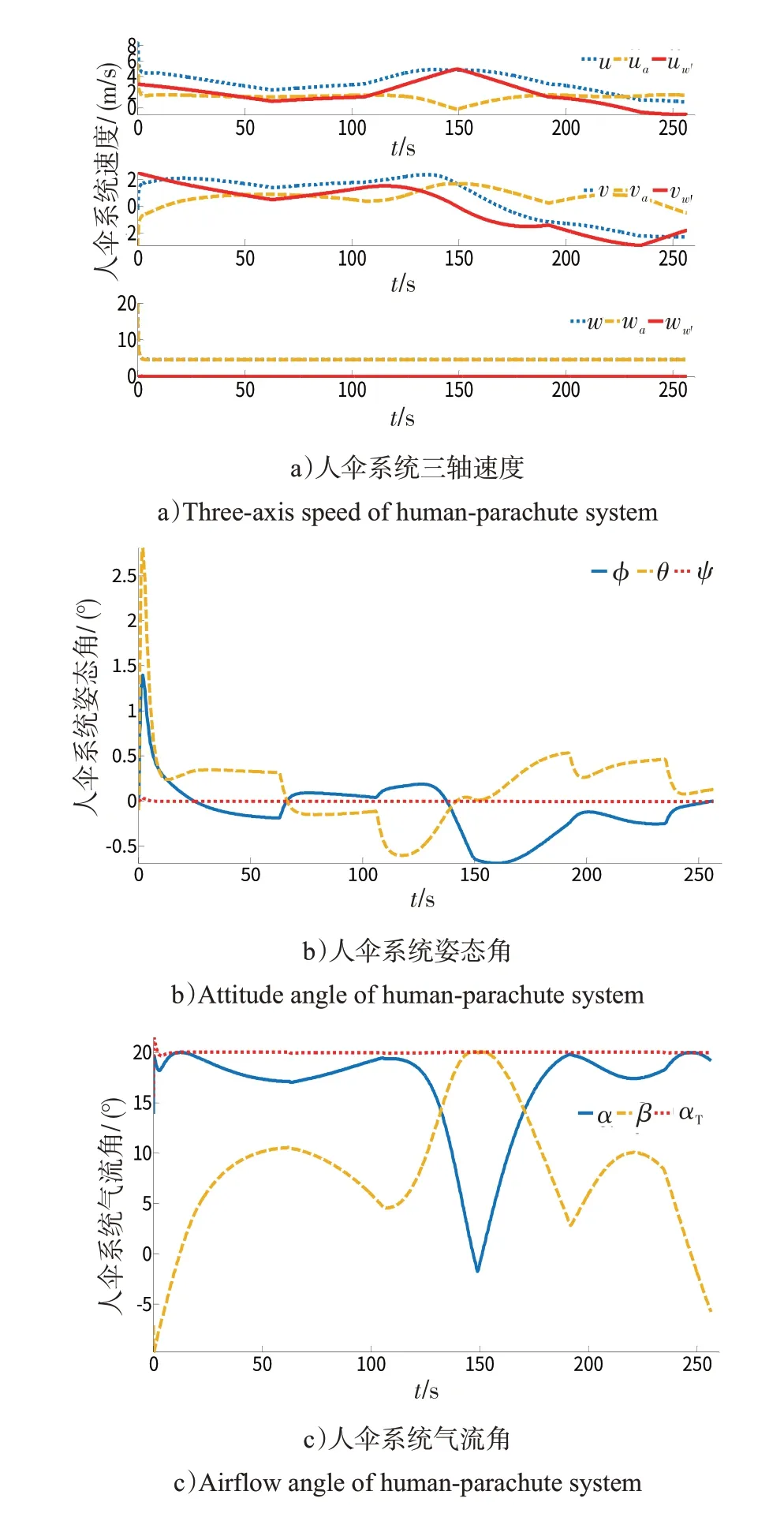
图18 有风情况下的人伞系统参数仿真曲线Fig.18 Simulation curve of parameters of human-parachute system with wind disturbance
5 结论
针对某型飞行员跳伞模拟器动力学建模需求,本文对人伞系统惯性参数进行了建模研究,分别构建了伞衣、伞绳、人体的转动惯性参数计算模型,并构建了典型仿真案例,对人伞系统惯性参数进行了数值分析,从数值计算结果可以看出,人伞惯性系统中,x
轴和y
轴转动惯量主要由人体产生,z
轴方向的转动惯量主要由伞衣和伞绳产生。本文的研究结果可为后续人伞系统动力学建模提供参数支撑。