基于DFT的布林线视角下的信号异常值检测方法
2021-09-01王亚蛟薛国欢
王亚蛟,薛国欢
( 92706部队,浙江宁波 315813)
近年来,随着对装备维修认识的深化,人们越来越关注装备在整个生命周期的健康状态。因此,装备健康管理应运而生,旨在通过监测其运行过程中出现的异常情况,提高视情维修的针对性和有效性。当个别信号测定值与信号均值的偏离程度比较大时,称之为异常信号。对于维修保障而言,挖掘出有价值的异常信号尤为重要,它是装备健康管理的重要环节。
多数情况下,从因果关系上无法判断信号是否异常,只能通过数理统计来发现有价值的异常信号。目前,有关异常信号检测的研究大多集中在频域,常采用傅里叶变换、小波变换算法。文献[10]实时掌握频谱动态变化,采用与历史扫频数据均值做差法来检测异常信号,但此法只能发现异常频率,不能定位到异常信号。文献[11]通过将不完整数据中的未缺失参数与具有完整数据的正常信号数据集进行比较,计算不完整数据的异常概率并检测出部分异常信号,但是在异常概率的计算中未考虑信号的概率分布特征。如何将频域的周期性和时域的统计性相结合,成为研究异常信号检测的重点内容。
在影响导弹长期贮存可靠性的关键部件中,远程转换开关、雷达角自动装置、弹上电源的特征电压值也服从于正态分布。本文以它们的定期检测数据为样本,利用离散傅里叶变换(Discrete Fourier Transform,DFT)对信号进行频谱分析,选择幅值大的低频谐波的周期,作为布林线的计算步长。根据正态分布和不同置信度确定布林线的轨道,为装备关键部件的运行状态细致划分了不同程度的异常区域。通过对测试数据的分析,对关键部件异常状态及时做出准确的判断,为导弹装备制定及时合理的维修决策提供指导。
1 相关理论
20 世纪70 年代,John Bollinger 提出了布林线理论。他在95%的置信度下,利用正态分布计算出股价运行的安全通道,其理论具有很强的实用性。
1.1 正态分布
正态分布是发明布林线的理论基础,它在数学、物理及工程等领域有着重大的影响力。若随机变量X
的概率密度函数为:
1.2 布林线数学模型
布林线由3条线组成:上轨线、中轨线和下轨线。在t
时刻以前,取随机变量x
,x
,…,x
-作为样本,符合正态分布,其计算步长为n
。设t
时刻数据的平均值为MB,标准差为σ
,调整参数为k
(k
>0),则: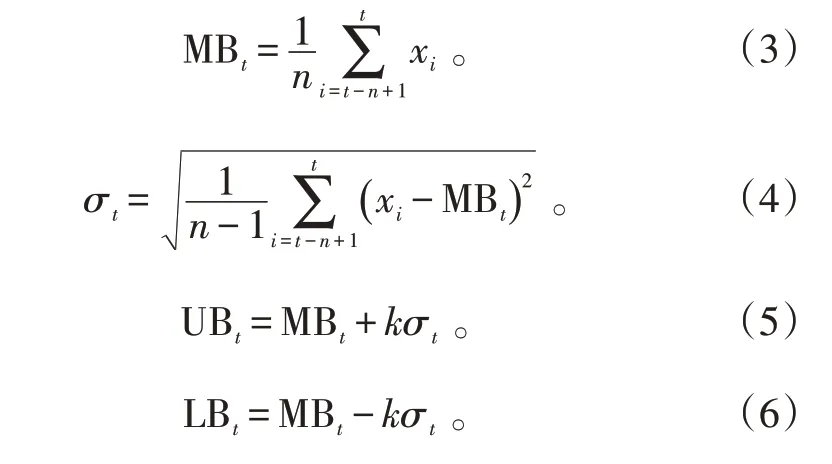
1.3 异常区域界定

α
与调整参数r
之间的关系。根据小概率原理,概率小于5%的事件,在1 次试验中被认为是几乎不可能发生的。如果信号落在[μ
-rσ
,μ
+rσ
] 区间外的概率1-α
小于5%(相当于α
大于95%),那么该信号为一般异常信号;如果其概率小于1%(相当于α
大于99%),那么该信号为格外异常信号。为了衡量状态的异常程度,将概率小于5%的区域再进行细分。根据95%和99%的置信度,经计算查表得到相应的调整参数和上、下轨值,如表1。

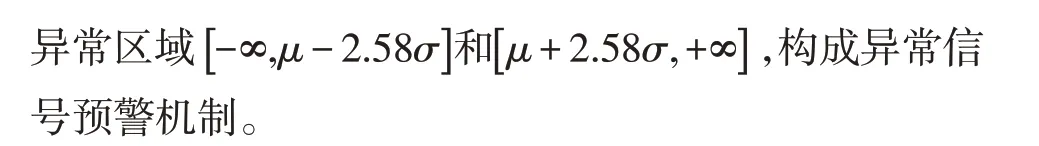

表1 不同置信水平下的布林线参数Tab.1 Parameters of Bollinger bands under different confidence levels
2 基于DFT的计算步长选取
在绘制布林线时,需要计算每个点的平均数和方差,关键在于确定布林线的计算步长。
从频谱的角度考虑,在DFT 中,信号是由不同幅值的谐波合成的,其中幅值大的谐波是信号的主要成分,保留了大部分信号的统计特性,能够充分反映数据的离散程度。幅值最大的谐波有高频和低频之分,由于高频对应的周期小,样本容量小,易产生虚警,故选择低频谐波的周期为佳。布林线的计算步长应采用幅值大的低频谐波的周期。下面从理论上进行分析。
2.1 离散傅里叶变换
傅里叶变换是1 种信号频域分析的方法,它将信号分解为不同频率的正弦波的叠加,然后由正弦波的频率和幅值构成幅度谱。

在实际应用中,快速傅里叶变换算法(Fast Fourier Transform,FFT)复杂度低,便于实现信号频谱的提取[16-17]。
2.2 频谱特性与步长选取

所以,


3 测试数据与结果分析
在导弹贮藏可靠性评价过程中,最易退化的关键部件如远程转换开关、雷达角自动装置、弹上电源等起着决定作用。根据相关工程经验,上述部件特征电压值的技术标准分别为27 V、1.95 V、36 V。通过定期(间隔6 个月)检测,得到1 套导弹2000—2010 年间共20组数据,如表2所示。
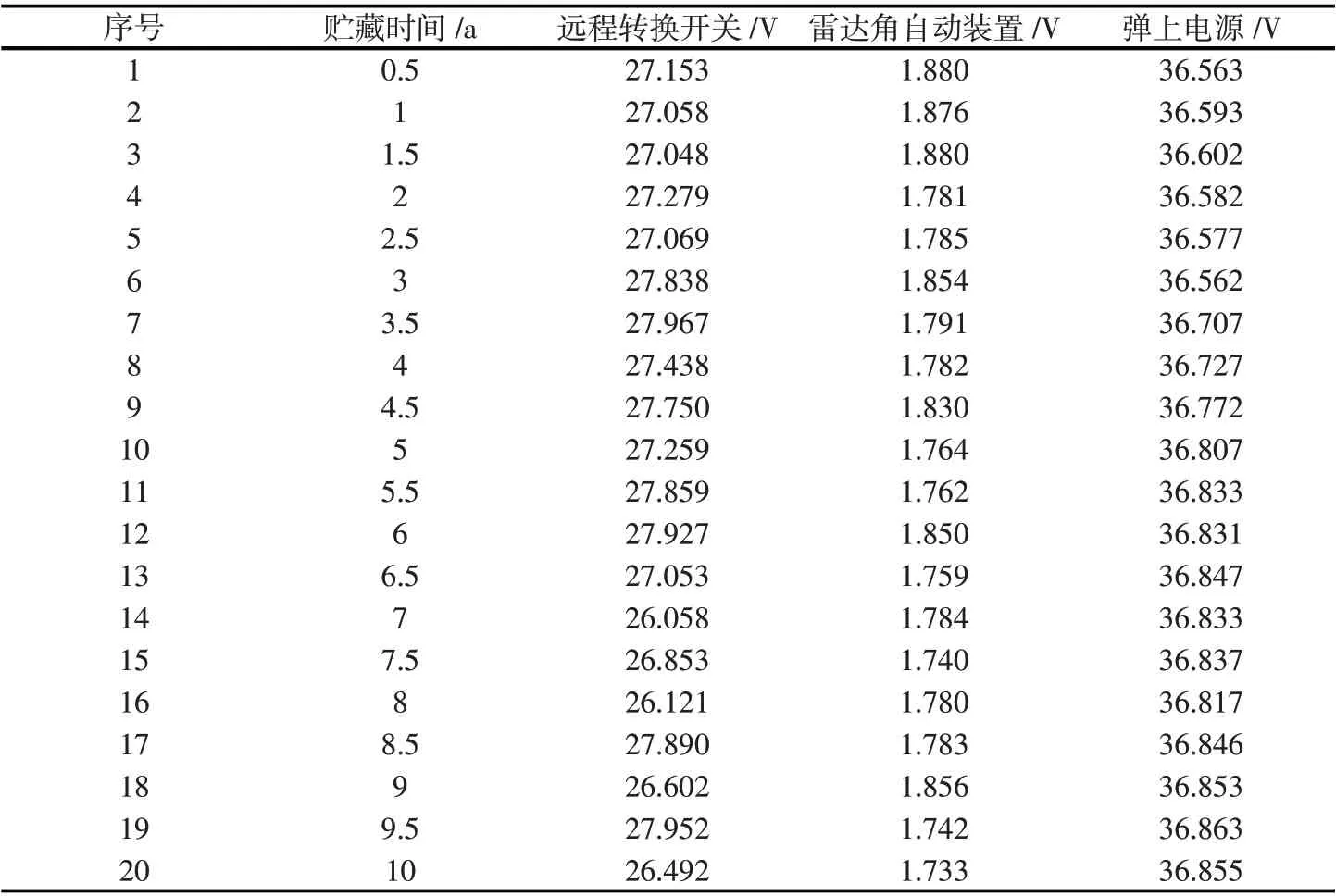
表2 导弹各关键部件特征电压值Tab.2 Characteristic voltage values of key components of the missile
通过表2 中的测试数据可以看出,电压值的变化呈现出杂乱的随机性,没有明显的规律性。为反映导弹状态退化过程中的异常点,下面对测试数据进行FFT算法处理并绘制步长适当的布林线。区分正常区域、一般异常区域和格外异常区域并找出异常点,结合均值和方差的变化趋势,进一步分析异常点的合理性。
测试数据的采样点数为n
=20 ,采样间隔T
=0.5a
,采样频率f
=1/T
=1/(0.5a
)=2a
。1 组数据的整个时间间隔为T
=nT
=20×0.5a
。如果对1 组数据作离散傅里叶变换,则基频为:
k
次谐波对应n
/k
个采样周期。若k
次谐波是数据的主要成分,则布林线计算步长应选择n
/k
个点。在布林线计算的初始阶段,历史数据不足n
/k
个时,则悉数全用。通过FFT 算法,得到远程转换开关的幅度谱图1a),可以看出2 次谐波的幅度值较大,是电压数据的主要成分,谐波波长作为远程转换开关布林线的计算步长的首选。由式(24)得,计算步长为20/2=10,得到图1b)的第1 幅布林线。其中,绿线对应置信度为95%布林线的上、下轨,红线对应置信度为99%布林线的上下轨,可以发现第6、14 个点处于格外异常区域。如果选择幅度值较小的5次谐波波长作为其布林线的计算步长,由式(24)得,计算步长为20/5=4,得到图1b)的第2幅布林线,并未发现第6、第14个点异常。
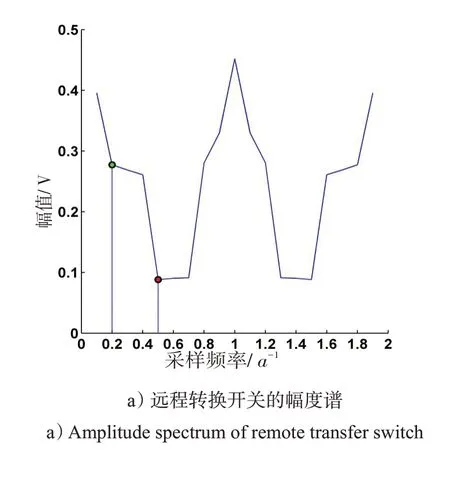
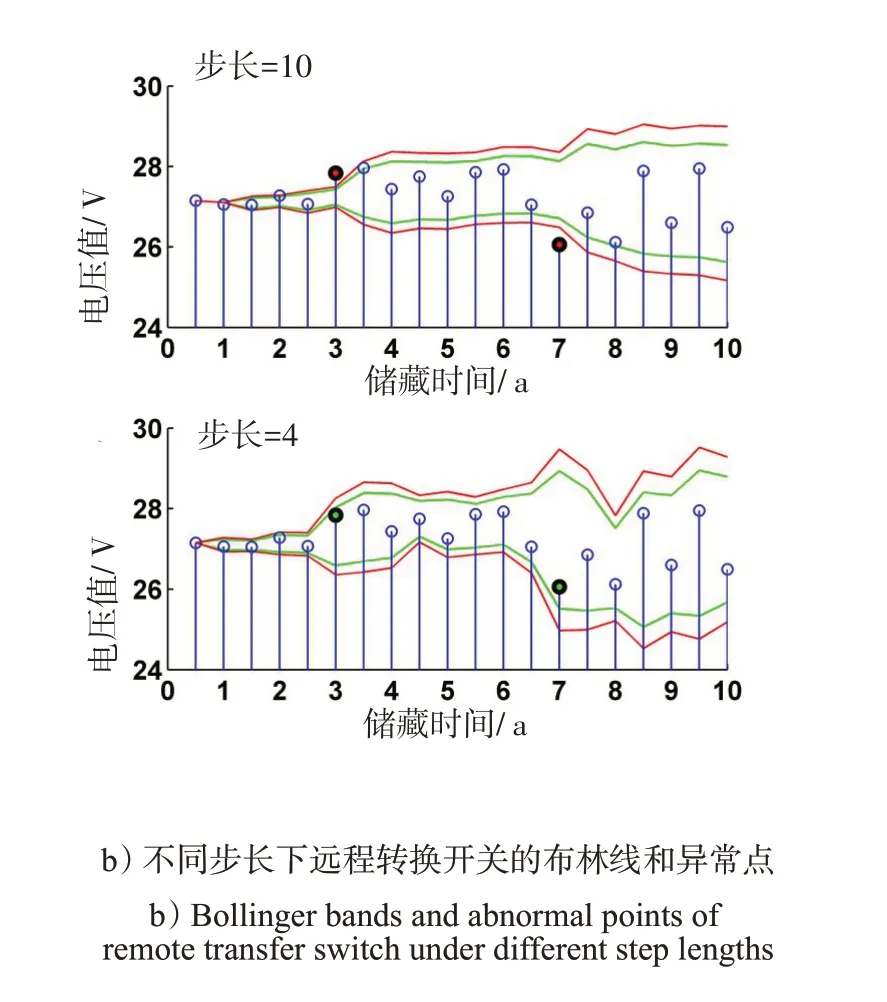
图1 基于FFT算法的不同步长布林线视角下的远程转换开关异常电压Fig.1 Abnormal voltage of remote transfer switch from the perspective of Bollinger bands based on FFT algorithm
第6、14个点是在概率为99%的异常点,这2个点将整个区间划分成3 个阶段:1~5、7~13、15~20。标准差逐渐增大,稳定性越来越差,说明将这2个点判为异常是合理的,步长选择方法是有效的。
通过FFT 算法,得到雷达角自动装置的幅度谱图2 a),可以看出4次谐波的幅度值较大,是电压数据的主要成分。由式(18)得,计算步长为20/4=5,得到图2 b)的第1幅布林线,绿线和红线的含义同上,可以发现第4个点、第18个点处于格外异常区域。如果选择幅度值较小的3 次谐波波长是其布林线的计算步长,由式(18)得,计算步长为20/3=6,得到图2 b)的第2幅布林线,并未发现第4个和第18个点异常。

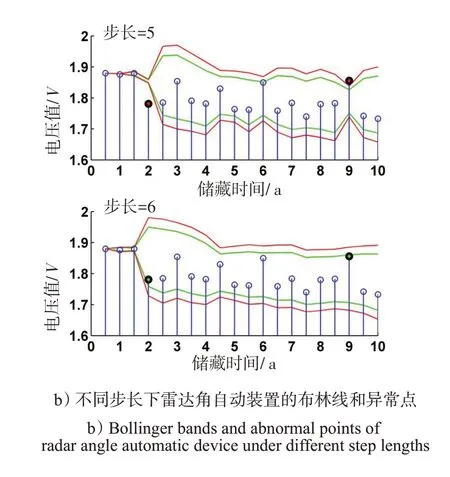
图2 基于FFT算法的不同步长布林线视角下的雷达角自动装置异常电压Fig.2 Abnormal voltage of radar angle automatic device from the perspective of Bollinger bands based on FFT algorithm
第4、18个点是概率为99%的异常点,从图2 b)看出,自第4个点开始均值变小,标准差变大,波动变大,因此第4 个点应判为异常点。第18 个点处均值和方差并未明显变化,且第6、第12、第18个点处于同一水平位置,间隔为3 a,断定为雷达角自动装置定期标校后的性能提升。通过FTT算法,得到弹上电源的幅度谱图3 a),可以看出2次谐波的幅度值较大,是电压数据的主要成分。由式(18)得,计算步长为20/2=10,得到图3 b)的第1幅布林线,绿线和红线的含义同上,可以发现第7个点处于格外异常区域,第8、9个点处于一般异常区域。如果选择幅度值较小的7次谐波波长作为其布林线的计算步长,由式(18)得,计算步长为20/7=3,得到图3 b)的第2幅布林线,并未发现第7、第8、第9个点异常。
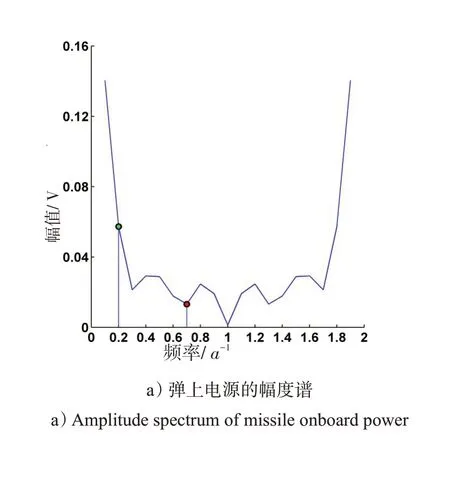

图3 基于FFT算法的不同步长布林线视角下的弹上电源异常电压Fig.3 Abnormal voltage of missile onboard power from the perspective of Bollinger bands based on FFT algorithm
第7个点是概率为99%的异常点,第8、9个点是概率为95%的异常点,将整个区间划分成3个阶段:1~6、7~10、11~20。前6个点均值稳定,波动较小;后10个点同样均值稳定,波动较小;第7~9个点电压剧烈升高,是1个稳态向另1个稳态迁移的中间过程。所以第7~9个点判断为异常点是合理的。
4 结束语
异常信号检测是装备健康管理的重要环节,为制定合理的维修决策提供依据,并提高系统运行的安全性和可靠性。文中针对导弹关键部件中常出现状态异常、性能退化问题,提出了一种兼顾时域统计性和频域周期性的异常信号数据检测方法。通过频谱分析选择布林线的计算周期。利用移动平均值和标准差确定布林线的轨道,为装备关键部件的运行状态细致划分了不同程度的异常区域,对导弹关键部件异常状态做出准确判断并及时维修,使得装备在必不可少的维修次数下保持完好状态。
