变温条件下的老化等效温度研究
2021-09-01李金飞柯慧剑李高春
刘 铁,李金飞,刘 克,柯慧剑,李高春
(1.海军航空大学,山东烟台 264001;2. 91115部队,浙江舟山 316000)
导弹等装备在其服役全寿命周期中,特别是在值班等环境中,由于存在季节和昼夜变化,导弹装备必将受到交变温度作用影响。由于导弹材料(如推进剂、橡胶等)的老化随温度变化,长期交变温度作用后,其产生累积效果如何计算以及实验室条件下如何计算上述老化等效温度等,是当前导弹加速贮存试验和寿命预估研究中的重要课题。
前期,国内外都开展了实际环境温度监测以及加速贮存试验方法研究。在环境监测方面,Richard开发了使用环境参数记录仪数据处理软件MLAD,并利用该软件对英国89 个导弹使用环境温度记录仪记录的温度数据进行了提取和分析。Yang给出了美国Alabama 地区的湿度年变化曲线,湿度变化与温度变化类似,都是随季节而变化。为模拟实际服役环境,进行加速贮存试验须将交变温度作用下等效环境温度作为其输入。池旭辉根据推进剂贮存环境的相关数据,建立了自然交变温度下老化等效温度的简化计算模型,从而为推进剂的老化评估提供了1 个简便的方法。张仕念等考虑导弹寿命周期内的实际环境温度数据,根据阿伦尼乌斯(Arrhenius)公式,得到了其贮存环境等效温度,从而为加速因子的计算提供数据。
本文对相关实测数据进行统计分析和处理,掌握导弹服役过程中环境载荷的特征和变化规律。根据Arrhenius公式,推导得到了变温环境下的老化等效温度。在此基础上,根据不同区域环境温度统计模型及数据,给出了不同变温情况下老化等效温度计算结果以及老化等效温度的影响因素,从而为变温条件下的老化计算和加速试验设计提供基础数据。
1 实测数据的分析与处理
为了获得露天堆放条件下贮存箱内的实际温度,用温度监测仪分别监测露天存放环境贮运箱上下堆放时箱内温度数据。采样频率为2 min/次。待试验结束后,取出温度监测仪并导出温度数据,4个木箱分别为A 箱、B 箱、C 箱、D 箱,所有箱内监测的温度数据,如图1 所示。从图1 中可看出,A、B 箱位于C、D 箱的上层,箱内温度较下层的高;A、C 箱位于B、D 箱的西侧,光照时间较长,箱内温度较高。

图1 贮箱内温度变化图Fig.1 Temperature change in four storage boxes
图2为监测的上(A箱)、下(C箱)层2年的温度数据,上层最高温度为51.6 ℃,下层最高温度为46.8 ℃,上、下层最低温度相差约为13.4 ℃。通过实测环境数据统计可知,上、下层年平均温度分别为15.7 ℃和15.1 ℃。由于受季节和昼夜变化的影响,自然贮存环境温度存在大幅值的季节和昼夜温差。受温度影响,其老化等效温度不能简单用某些特征温度(如中值温度、平均温度)表示。

图2 上、下层温度监测数据Fig.2 Temperature monitoring data of upper and lower boxes
2 变温环境下老化等效温度计算
假设影响部件失效的关键指标B
,其初始值为N
,当B
退化到N
时产生失效。关键指标根据实际情况选定,如推进剂的抗拉强度、延伸率,电子产品的测试电压、电流以及橡胶材料的压缩回弹率等。由于受温度长期影响,部件内部产生化学老化,从而产生失效。假设化学反应服从以下规律:

k
为反应率系数。假设在t
=0 时,N
=N
。由式(1)~(3)得到:
T
是指在相同时间内产生与变温条件相同的失效或退化效果的等效温度。老化等效温度可以有效考虑化学反应的情况,从而模拟服役条件下变温环境。假设B
经过一系列变温条件,在t
时间内,其反应率为k
;在t
时间内,其反应率为k
;经过i
个时间段后: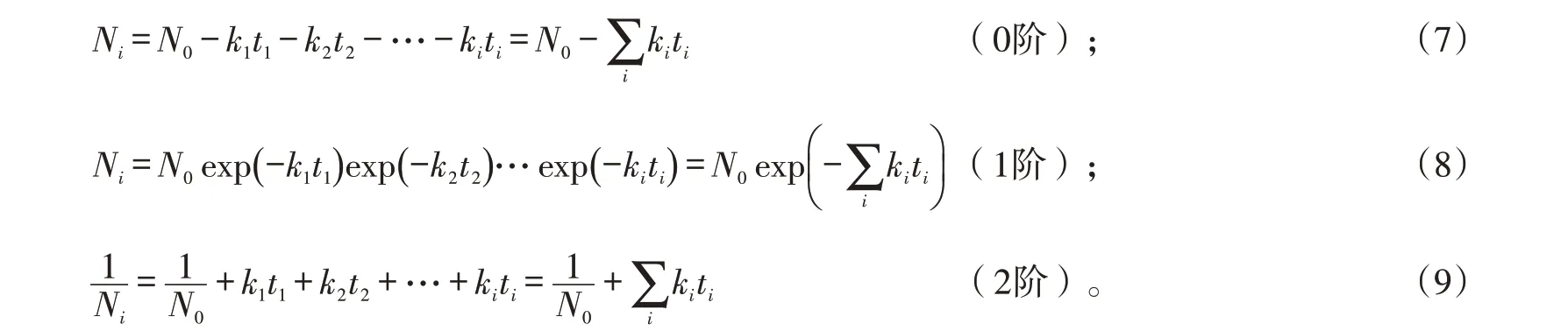

E
为活化能;k
=8.
61×10eV/K ,为Boltzmann常数;T
为t
时间内的绝对温度。反应速率为k
相对应的老化等效温度为T
。则:

T
与算术平均温度不同,与老化过程的活化能等相关,是考虑温度影响后,通过加权平均得到的温度。3 计算结果及分析
3.1 基于实测环境温度的老化等效温度计算
基于实际测得的环境温度数据,得到不同活化能条件下的上、下层贮箱内的老化等效温度,结果如表1所示。由表1可知,在交变温度条件下,老化等效温度与平均温度不同。一般情况下,老化等效温度要大于平均温度(上、下层年平均温度分别为15.7 ℃和15.1 ℃)。另外,下层老化等效温度要低于上层,这样可以对导弹部件进行有效防护,可以降低老化等效温度,从而减少贮存过程中老化影响。随着活化能的增高,老化等效温度增加(见图3),由于活化能更高,材料老化反应需要更多的能量,因此,变温条件下的高温环境具有更高的权重。
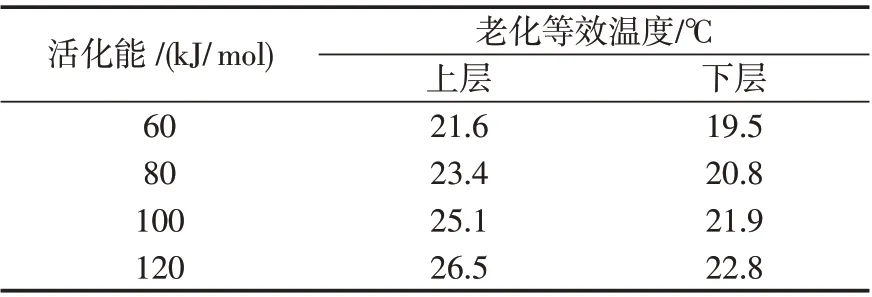
表1 不同活化能条件下的老化等效温度Tab.1 Aging equivalent temperature under different activation energies
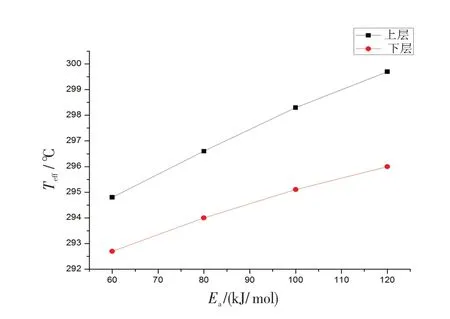
图3 活化能对老化等效温度的影响Fig.3 Influence of activation energy on aging equivalent temperature
3.2 基于环境温度模型的老化等效温度计算
在没有实测环境数据的情况下,可以根据记录的最高温和最低温,建立相应的环境温度模型。根据相应的温度环境模型,计算得到相应的等效环境温度,为开展时间的加速老化试验奠定基础。
统计数据表明,不同区域环境温度具有明显的周期性,可用多个余弦级数叠加得到:
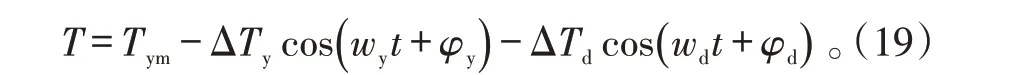
T
为年平均温度;ΔT
为季节温度幅值;ΔT
为日温度幅值;w
为季节变化频率,其值为2π 365×24;w
为日变化频率,其值为2π 24;φ
、φ
分别为对应于w
、w
的相位角;t
为时间,单位h。考虑其周期性特点,为简便起见,设日温度幅值为日温度幅值的平均值,同时假设t
=0 时为年温度最低时刻,则φ
、φ
为0。通过整理相关气象资料,可得3个海区某典型区域的年温度变化公式如下。北海:
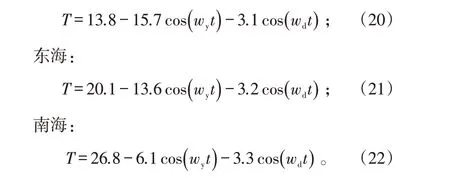
由式(20)~(22)可知,3 个海区由北向南,环境温度年平均值逐渐增大,季节变化幅值逐渐减小,而昼夜变化幅值基本相同。
根据式(10),通过离散积分得到各海域的老化等效温度,如表2所示。
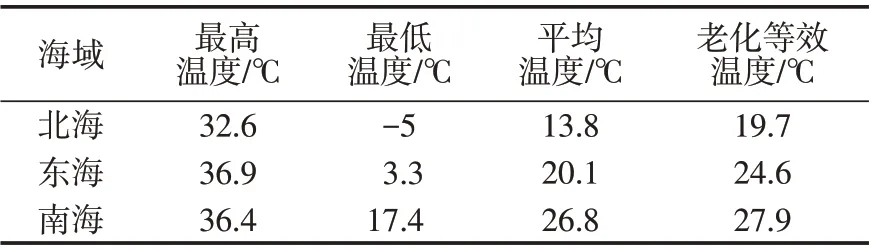
表2 典型海域老化等效温度Tab.2 Aging equivalent temperature of typical sea area
由表2分析得到,老化等效温度与平均温度不同,对于温差越大的环境,老化等效温度与平均温度差异越明显,如图4 所示。在温差大的地域应当考虑交变温度产生的老化累积效应。
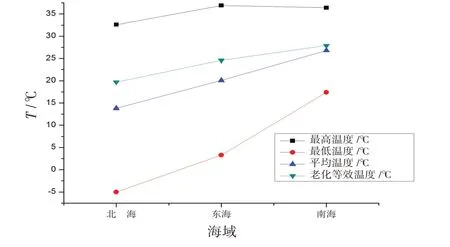
图4 不同海域温度计算结果Fig.4 Temperature calculation results of different sea areas
在高温海区贮存,虽然其温度变化幅度较小,但由于长期高温,且温度是影响老化的主要因素,其老化等效温度将增加,产品长期老化累积也将增加,更容易老化失效。做好发射箱高温条件下的降温工作,可以有效减少老化影响,从而提高其贮存寿命。
4 结论
本文对相关实测数据进行统计分析和处理,掌握环境温度的变化规律。根据Arrhenius公式,推导得到了变温环境下的老化等效温度,给出了变温情况下老化等效温度计算结果,并分析其影响因素。研究表明,
1)环境温度受到季节以及昼夜变化的影响,呈现交变的特点;堆放条件下,上、下层贮箱内的温度变化规律基本相同,但存在一定的温差。
2)老化等效温度大于平均温度,并受到活化能的影响,活化能增高,老化等效温度也随之增加。
3)温差越大的环境,老化等效温度与平均温度差异越明显。在高温海区贮存,虽然其温度变化幅度较小,但其老化等效温度将增加,产品长期老化累积也将增加。
