基于一元二次函数的层联机织预制体细观结构表征
2021-08-31任丽冰
任丽冰, 陈 利, 焦 伟
(1. 天津工业大学 纺织科学与工程学院, 天津 300387; 2. 天津工业大学先进纺织复合材料教育部重点实验室, 天津 300387)
纺织复合材料具有质量轻、比强度高、力学性能可设计等优点,在航空航天、高端民用等领域具有广阔的应用前景。采用各种纺织预制体增强的纺织复合材料具有复杂多样的细观结构,合理建立纺织预制体结构参数之间的关系,表征其细观结构,是高性能复合材料设计的关键问题。
层联机织预制体是高性能复合材料的理想增强材料之一,其独特的层间纤维弯曲连接的细观结构显著提高了复合材料的层间性能,同时满足了复合材料的可加工要求,近年来得到迅速发展。层联机织预制体具有复杂的三维整体细观结构,结构参数之间相互影响给复合材料细观结构分析带来巨大困难。影响层联机织预制体细观结构的因素主要包括组织结构、经纬纱密度、纱线线密度、纱线层密、纱线横截面形态、纤维体积含量等,其中合理的纱线横截面假设是建立结构参数关系的关键[2-4]。
前期研究建立的纱线横截面假设是以圆曲线凸透镜形为主,是以2个相同半径的圆弧曲线围成的一个凸透镜。表征凸透镜横截面形状的关键参数包括圆弧半径、厚度和长短径比。凸透镜长短径比又称为纱线截面变异系数λ。基于圆曲线凸透镜假设的纱线横截面在织物细观结构中存在着几何参数的不确定性,即纱线截面变异系数λ不能直接计算获得。杨彩云等[5]通过拟合三维机织预制体结构参数与预制体厚度之间的关系, 提出了凸透镜截面变异系数λ计算的经验公式[6];郑君等[7]和Dong等[8]通过已知的预制体厚度,由迭代计算方法获得λ。更多的学者是通过实际观测纱线截面的宽度和厚度来确定二者的比值λ[9-10],获得的纱线横截面变异系数仅适用于既定样品。本文提出基于一元二次函数的经纱抛物线路径和纬纱抛物线凸透镜横截面等假设,构建了明确的微观几何关系,获得了纱线横截面变异系数,进而建立层联机织预制体的细观结构几何模型,通过对预制体厚度和纤维体积含量的计算,验证模型的有效性和合理性。
1 层联机织预制体组织结构
层联机织预制体由多层经纱和纬纱交织而成。经纱沿织物成型方向呈现波浪弯曲形状,将相邻的2层纬纱联接在一起,纬纱垂直于织物成型方向呈现伸直状态,结构如图1所示[11]。
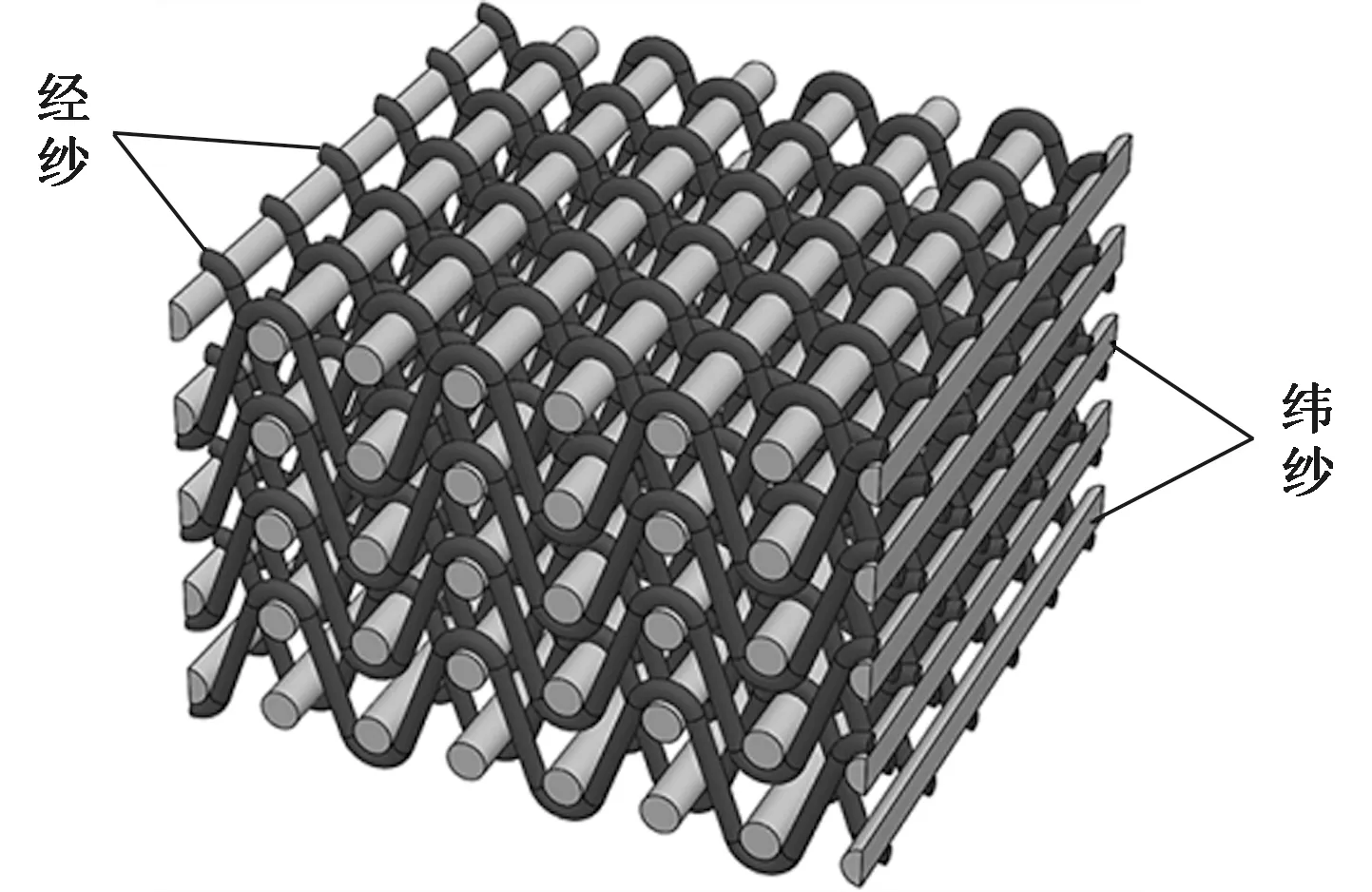
图1 层联机织预制体示意图Fig.1 Illustration of multi-layer interlocked woven preform
层联机织预制体的基本组织结构为多层平纹层间联锁结构,即结构中经纱分别按照平纹一上一下的交织规律与相邻的2层纬纱交织。图2示出层联机织预制体表面经纬纱交织结构和层间经纱路径。
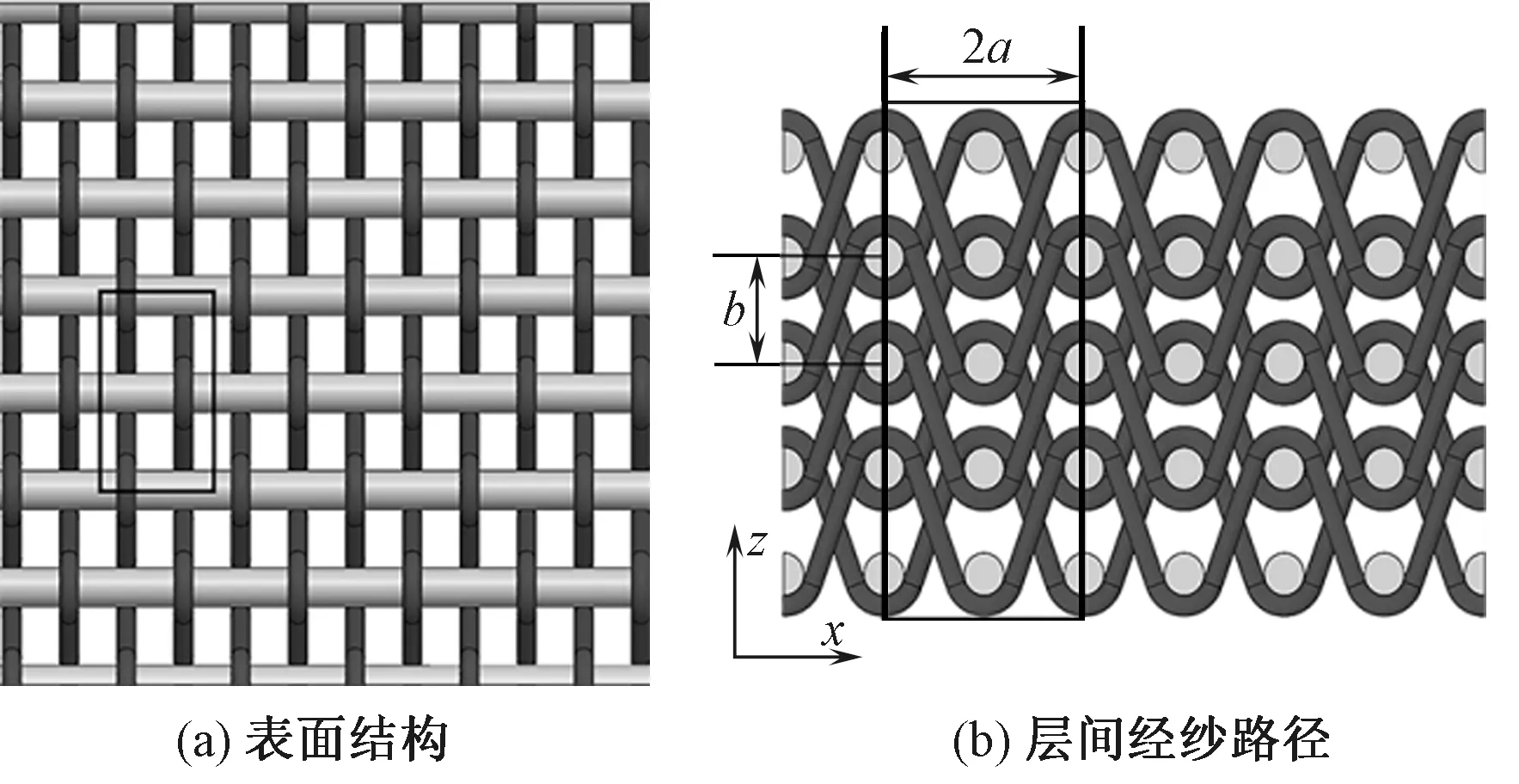
图2 层联机织预制体结构示意图Fig.2 Structure of multi-layer interlocked woven preform. (a) Surface structure; (b) Warp yarn paths in perform
采用Micro-CT扫描方法表征层联机织预制体的纱线交织形貌,如图3所示。

图3 层联机织预制体中纱线交织形貌Fig.3 Mixed morphology path in multi-layer interlocked woven preform. (a) Micro-CT image of preform; (b) Warp weave cross-section; (c) Weft weave cross-section
由图3可知:经纱路径为波浪弯曲形态,贯穿相邻2层纬纱;沿纬纱长度方向的纬向截面中纬纱路径轻微弯曲,近似为直线形状。
图4示出层联机织预制体中纱线的截面形貌。可知,截面中预制体内部的纬纱受到内部经纱的环绕挤压作用,其横截面呈现凸透镜形状,而预制体上下表层的纬纱在表层经纱环绕挤压下,其横截面近似为拱形。在2列纬纱之间剖取3个不同位置的纬向截面,观察其中经纱截面形状变化可知:1-1截面位于纬纱轴线位置,截面为经纱的横截面,近似为倒梯形;2-2截面位于2列纬纱之间,截面为经纱的斜截面,近似为矩形;3-3截面位于纬纱轴线位置,截面为经纱的横截面,近似为正梯形。

图4 层联机织预制体中纱线截面形状Fig.4 Yarn sectional shapes in multi-layer interlocked woven preform. (a) Weft cross-section; (b) Warp section
2 层联机织预制体微观几何建模
2.1 纱线横截面假设
2.1.1 经纱横截面
由图4(b)可知,沿经纱长度方向不同位置的经纱截面形状不同,从倒梯形到矩形再到正梯形逐渐变化。在1-1和3-3截面中,同层相邻经纱沿织物宽度方向挤紧,正梯形截面与倒梯形截面间隔排列,且在厚度方向上经纱与纬纱相互挤紧。而在2-2截面中,同层矩形截面的经纱沿宽度方向相互紧密排列,但在厚度方向上经纱间存在少许间隙。从图中还可以看出:1-1和3-3截面中经纱梯形截面的中位线的宽度近似相等,且等于2-2截面中经纱矩形截面的宽度;而1-1和3-3截面中经纱梯形截面的厚度小于2-2截面中经纱矩形截面的厚度,这主要是由于1-1和3-3截面中的经纱截面为其横截面,而2-2截面中的经纱截面为其斜截面。为便于建模,忽略经纱横截面沿长度方向的挤压变形,假设经纱横截面沿长度方向保持不变,形状简化为矩形,其宽度近似为梯形横截面的中位线宽度,如图5所示。
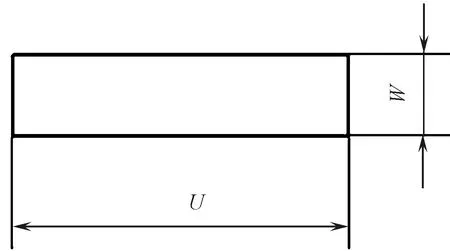
图5 经纱横截面形状Fig.5 Warp cross-sectional pattern
同层经纱相互挤紧,则经纱横截面宽度U(mm)和厚度W(mm)分别为
(1)
(2)
式中:Pj为经纱密度,根/cm;S1为经纱横截面面积,mm2。
则经纱横截面变异系数μ为
(3)
2.1.2 内部纬纱横截面
根据图4(a),假设层联机织预制体内部纬纱的横截面形状为抛物线凸透镜形,如图6所示。其由2个一元二次函数曲线Z1和曲线Z2围成。
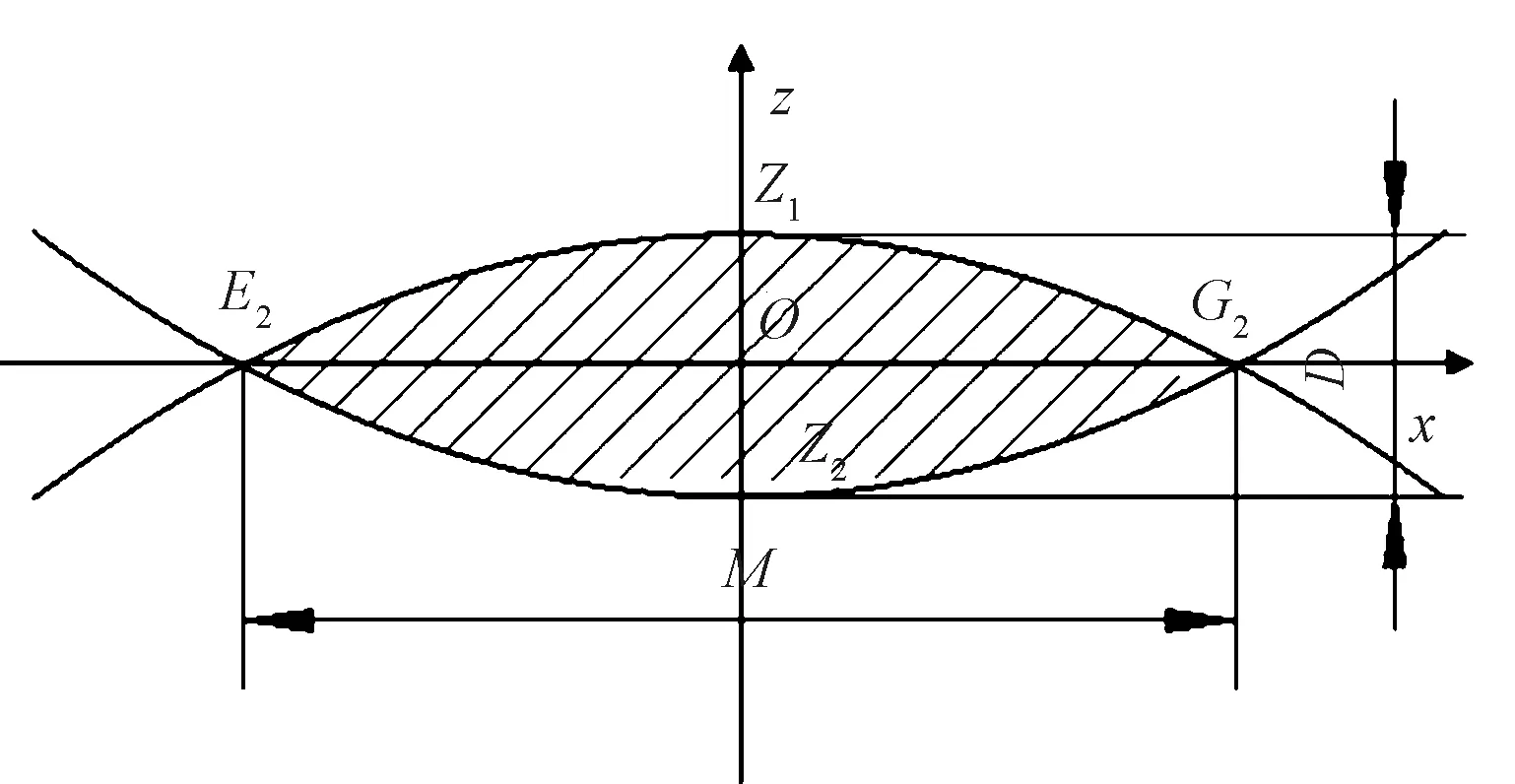
图6 层联机织预制体内部纬纱横截面形状Fig.6 Interior weft cross-sectional pattern of muti-layer interlocked woven perform
设内部纬纱横截面的厚度为D(mm),宽度为M(mm),曲线Z1表示为
(4)
内部纬纱横截面的面积为
(5)
则内部纬纱横截面变异系数λ为
(6)
2.1.3 表层纬纱横截面
根据图4(a)假设层联机织预制体表层纬纱的横截面形状为抛物线拱形,如图7所示。其由3个一元二次函数曲线Z1、Z4和Z5围成,曲线Z5为曲线Z4的偏移曲线。
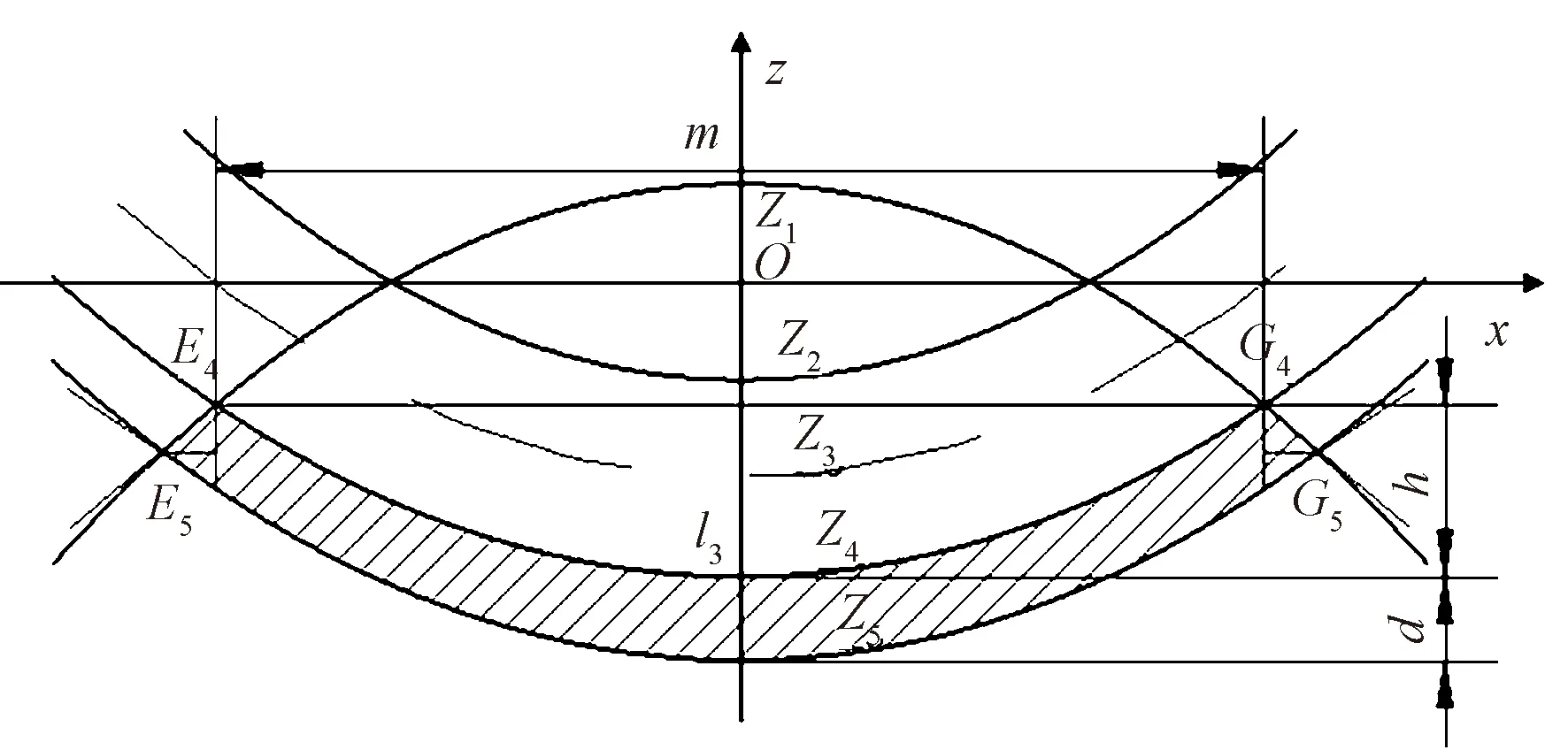
图7 层联机织预制体表层纬纱横截面形状Fig.7 Surface weft cross-sectional pattern of muti-layer interlocked woven perform
设表层纬纱拱形横截面厚度为d(mm),横截面的内拱高为h(mm),内拱宽度为m(mm),则表面纬纱横截面面积近似为
(7)
设拱形横截面的内拱弧长为l3(mm),则表层纬纱横截面变异系数τ为
(8)
2.2 纬纱横截面变异系数
根据图4(a),层联机织预制体纬纱与经纱相互交织规律,建立预制体细观结构分析模型如图8所示。纬纱与相邻的经纱相互挤紧交织。
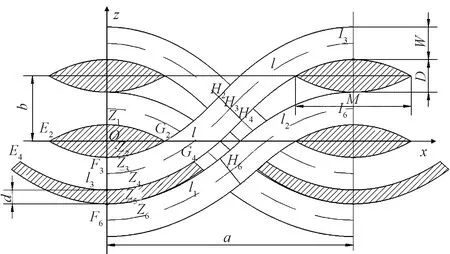
图8 层联机织预制体结构几何模型Fig.8 Geometrical model of multi-layer interlocked woven preform
2.2.1 内部纬纱横截面变异系数
由图8可知,内部经纱的中心路径Z3可由抛物线方程表示为
(9)
式中,a为层联机织预制体的纬纱间距,mm。
点H2到曲线Z3的距离为W/2,则该点的坐标为
(10)
(11)
内部纬纱横截面的下边界抛物线Z2表示为
(12)
曲线Z2经过点H2,将式(10)和(11)代入式(12)得到
(13)
根据式(5)和(13),用数值方法获得内部纬纱横截面厚度D,由式(6)得纬纱横截面变异系数λ。
2.2.2 表层纬纱横截面变异系数
表层经纱的中心路径由抛物线Z6表示为
表面纬纱的内拱抛物线Z4过点H4,可表示为
(15)
式中:
XH4和ZH4为H4的坐标值,该点到曲线Z3的距离为W/2。曲线Z4与Z1的交点为E4和G4,E4与G4关于x轴对称,G4的坐标为
则表面纬纱拱形横截面的内拱弧E4G4的宽度m和高度h分别为
(16)
(17)
将式(16)、(17)代入式(7)得到表层纬纱横截面的厚度d。
表层纬纱拱形横截面的内拱弧E4G4的长度为
(18)
代入式(8)可得到表层纬纱横截面的变异系数τ。
2.3 预制体厚度
根据上述获得的微观几何关系建立层联机织预制体的全厚度单胞模型,如图9所示。
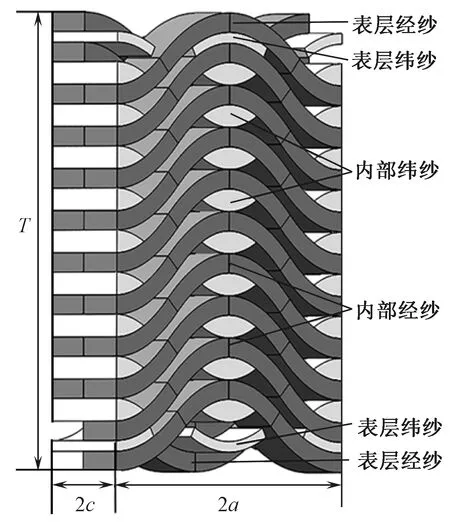
图9 层联机织预制体全厚度单胞模型Fig.9 Through-thickness cell model of multi-layerinterlocked woven preform
所建立的几何实体模型内经纱和纬纱相互挤紧交织且无纱线相互嵌入现象。设层联机织预制体的纬纱层数为N,其表层纬纱为2层,单层厚度为d;内部纬纱为N-2层,单层厚度为D;表层经纱为2层、内部经纱为N-3层,表层经纱和内部经纱横截面相同,单层厚度均为W。层联机织预制体的厚度T为
T=(N-2)D+2d+(N+1)W
(19)
2.4 预制体纤维体积含量
预制体的纤维体积含量为纤维体积占整体预制体体积的百分数,计算公式为
(20)
式中:Vf为纤维体积含量,%;Vj为经纱纤维所占体积;Vw为纬纱纤维所占体积,mm3;V为预制体体积,mm3。
由图8可知,一个纬纱间距内,内部经纱Z3由F3H3和H3I3曲线段组成,且2个曲线段的长度相等均为l:
(21)
内部经纱Z6由F6H6和H6I6曲线段组成,2个曲线段的长度为l1和l2,分别为
(22)
(23)

根据图9所示的预制体全厚度单胞模型,层联机织预制体的纤维体积含量为
Vf=
(24)
3 实验对比分析
3.1 纱线的横截面变异系数
本文设计了J8W2.50、J8W3.00和J8W3.15 3种结构层联机织预制体,结构参数见表1。3种预制体在天津工业大学复合材料研究院自主研发的立体机织设备上制备。采用Micro-CT扫描技术,获得了3种预制体的不同截面图如图10所示。采用Dragonfly图像处理软件测量了预制体纱线横截面的宽度、厚度及其面积。通过对比纱线的理论横截面面积,由测量的经纱横截面面积S1、内部纬纱横截面面积S2和表层纬纱横截面面积S3可以计算得到纱线填充因子ε1、ε2和ε3,如表2所示。可以看出,挤紧状态下层联机织预制体内3种纱线的填充因子近似相等,因此,可假设预制体内不同纱线的填充因子均为ε。

表1 层联机织预制体结构参数Tab.1 Structural parameters of multi-layer interlocked woven preforms
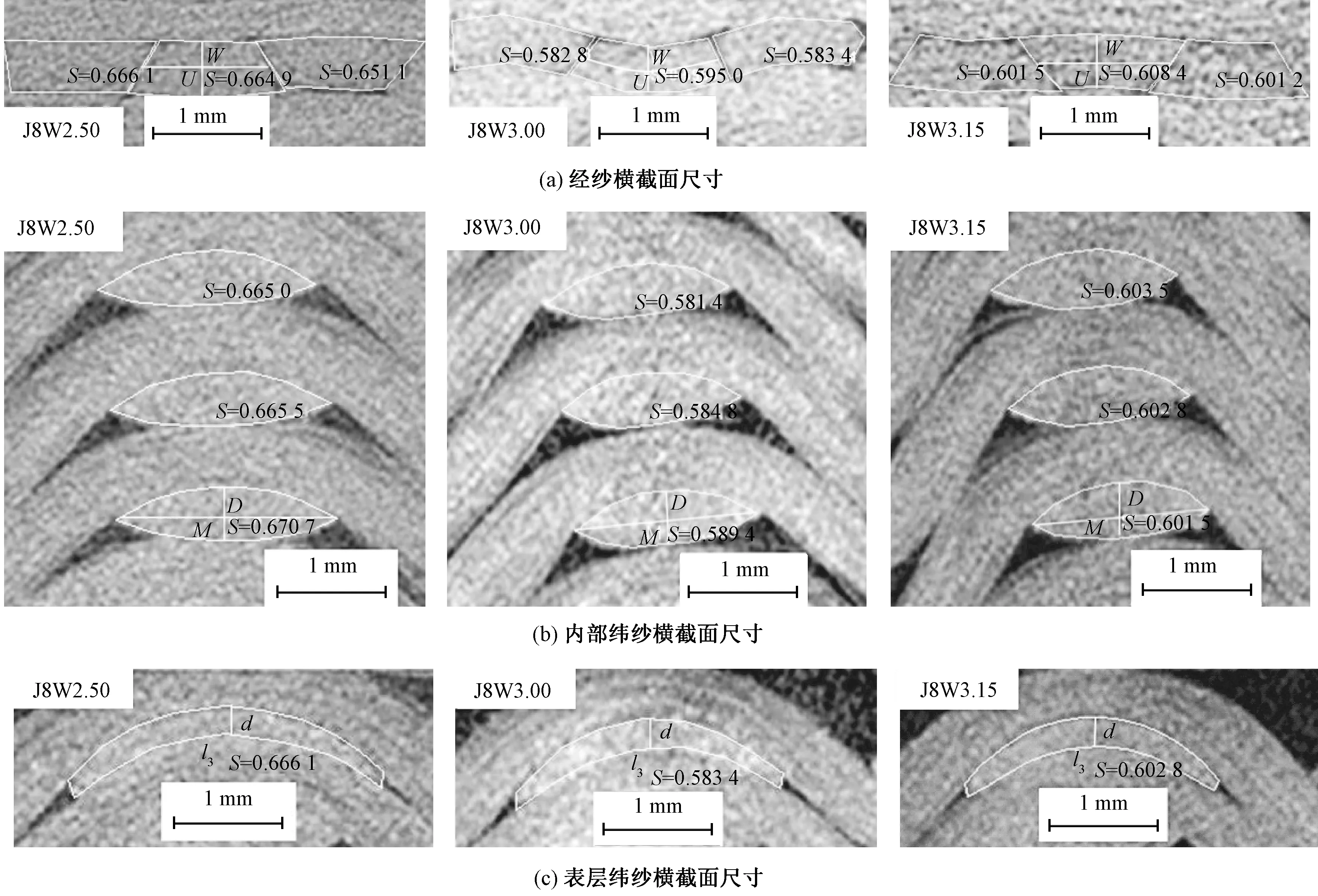
图10 层联机织预制体内部纱线横截面尺寸测量过程Fig.10 Measured yarn cross-sectional size of multi-layer interlocked woven preform. (a) Warp cross-sectional sizes; (b) Interior weft cross-sectional sizes; (c) Surface weft cross-sectional sizes

表2 层联机织预制体纱线填充因子Tab.2 Yarn packing factors of multi-layer interlocked woven preforms
根据实验结果,3种结构预制体的纱线填充因子分别取为0.75、0.85和0.825,计算获得3种预制体内经纬纱横截面的厚度和变异系数,如表3~5所示。
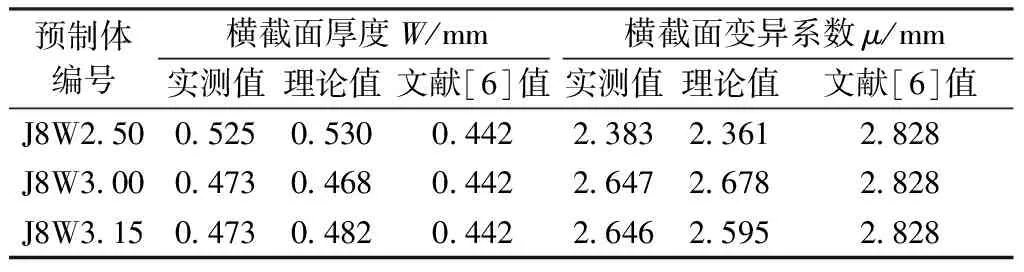
表3 经纱横截面的厚度和变异系数Tab.3 Thickness and variation coefficient of warp yarn cross sections
与实测值对比表明,理论计算值与实测值具有很好的一致性。同时,对比文献[6]方法获得的纱线横截面厚度和纱线横截面变异系数,本文模型获得的理论值更加接近实测值。

表4 内部纬纱横截面的厚度和变异系数Tab.4 Thickness and variation coefficient ofinterior weft yarn cross sections
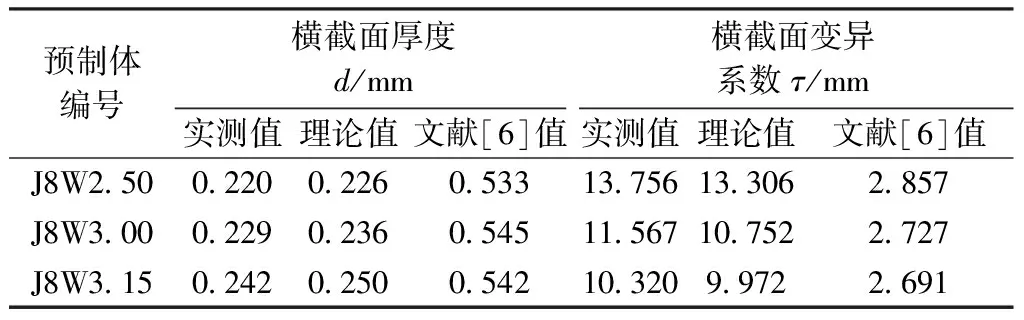
表5 表层纬纱横截面的厚度和变异系数Tab.5 Thickness and variation coefficient ofsurface weft yarn cross sections
3.2 预制体的厚度和纤维体积含量
由式(19)和(24)计算获得3种结构层联机织预制体的厚度和纤维体积含量如表6所示。通过与实测值对比表明,本文模型理论计算值与实测值具有很好的一致性。通过与文献[6]的理论计算结果对比显示,本文模型理论计算值具有更高的精度。

表6 层联机织预制体的厚度和纤维体积含量Tab.6 Thickness and fiber volume faction of multi-layer interlocked woven preforms
表7示出纱线填充因子与层联机织预制体厚度和纤维体积含量之间的关系,表中J8W2.50和J8W3.00预制体具有相同的经纬纱层数。可以看出,随着纱线填充因子的增大,预制体的厚度减小,纤维体积含量增大。当2种预制体纱线填充因子分别为0.750和0.850时,其厚度和纤维体积含量理论值分别与实测值最为接近。

表7 不同填充因子下的层联机织预制体厚度和纤维体积含量Tab.7 Thickness and fiber volume fraction of multi-layer interlocked woven preforms with different yarn packing factors
经密和纬密的变化会改变层联机织预制体的纱线填充因子和纤维体积含量,结果如图11所示。可知,随着经密或纬密的增大,预制体纱线填充因子和纤维体积含量随之增大。通常情况下,层联机织预制体纤维体积含量的取值区间为50%~60%,对应的纱线填充因子取值区间为0.73~0.87。
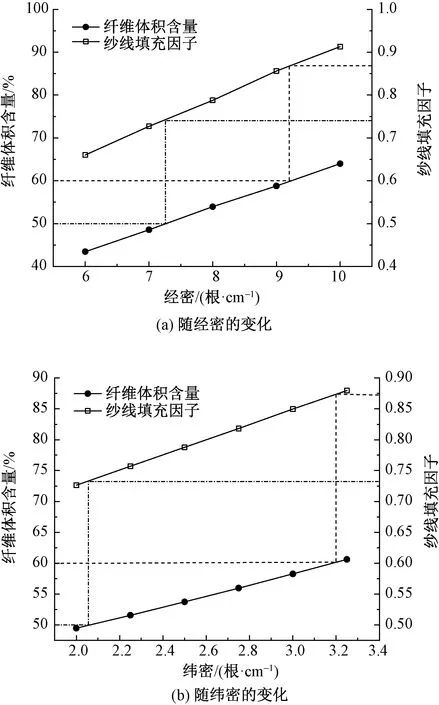
图11 纱线填充因子和纤维体积含量随纱线经纬密的变化Fig.11 Variations of yarn packing factor and fiber volume fraction with yarn warp density (a) andweft density (b)
4 结 论
本文在经纱抛物线路径和纬纱抛物线凸透镜横截面假设的基础上,建立了层联机织预制体的细观结构模型,通过实验验证得到以下主要结论。
1)基于一元二次函数定义的抛物线凸透镜内部纬纱横截面、抛物线拱形表层纬纱横截面以及抛物线形经纱路径,所建立的层联机织预制体细观结构参数关联关系是确定的、可求解的,可获得纱线横截面变异系数的确定解。
2)表层纬纱和内部纬纱具有不同的横截面形状,通过建立预制体的全厚度单胞模型,可准确预测预制体的厚度和纤维体积含量。
3)随着经纬密的增加,层联机织预制体的纱线填充因子和纤维体积含量随之增加,当纤维体积含量为50%~60%时,纱线填充因子的取值区间为0.73~0.87。
