探究高中数学新教材中互补角的应用问题
2021-08-31江苏省南京市临江高级中学乐晓梅
江苏省南京市临江高级中学 乐晓梅
2020 级高一是苏教版数学新教材使用的第一个学年,教师需要学好新课标、用好新教材,发现新教材中变化的方面,充分领悟编者的意图,从而更好地为教学服务。三角形是所有几何图形的基础,本文主要探究通过隐含的互补角,利用正、余弦定理解决三角形问题,在教学活动中发展学生的数学运算素养,进一步提高学生的数学思维品质。
一、运用互补角证明三角形中线长公式
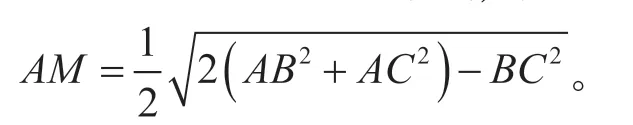
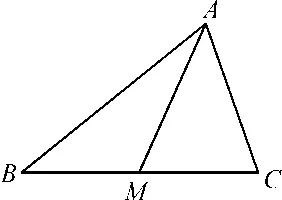
图1
这道例题出现在余弦定理这一节,因为涉及边的平方形式,等式结构特征明显,很容易让学生想到在三角形中运用余弦定理,又因为这些边分布在两个三角形中,所以分别在△AMB和△AMC中利用补角的余弦值相反,即cos ∠AMB=-cos ∠AMC。

二、运用互补角证明三角形角平分线定理
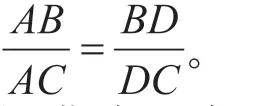


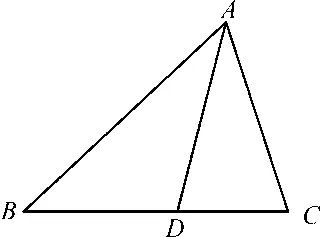
图2

学生活动1:你能用平面几何的方法来证明这个结论吗?
与边角有关,想到面积,探究面积法:

学生活动2:如果这个角平分线是外角的,会有什么结论呢?教材在95 页思考运用部分第9 题,为学生创设了活动平台。通过这些探究活动,让学生发现问题、探究问题和解决问题的能力得以提升。
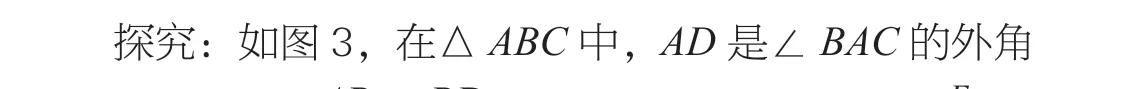
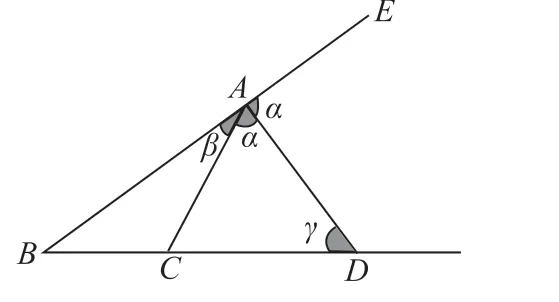
图3

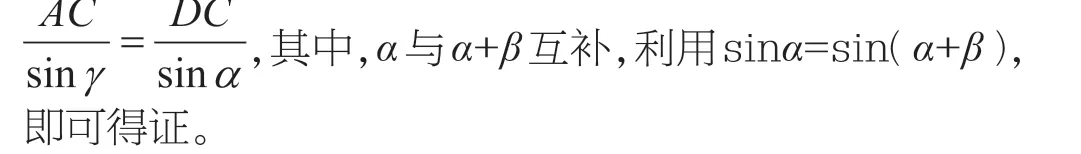
为了巩固补角关系在图形中的应用问题,编者在习题中设计了多个问题。
三、运用互补角求证四边形中的相关问题
1.平行四边形中对角线和边的关系

学生分析:根据式子结构特征,出现边的平方,易想到余弦定理,但三角形较多,要分别选择以AC、BD为边的三角形,我选择△ABC和△BCD:
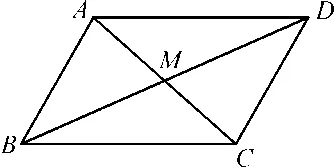
图4
△ABC中,AC2=AB2+BC2-2AB·BCcos ∠ABC,
△BCD中,BD2=BC2+CD2-2BC·CDcos ∠BCD,
∠ABC与∠BCD互补,即cos ∠ABC=-cos ∠BCD,两式相加即可得证。
余弦定理只能在三角形中使用,如何将四边形转化为三角形是关键,对四边形进行分割会出现多个三角形,选择哪些三角形又是一个关键点。在问题探索中加强了学生的分析能力。
2.圆的内接四边形中求值问题
探究拓展1:教材89 页第12 题。
(1)如图5,圆O的内接四边形ABCD,其中,AB=2,BC=6,CD=DA=4,求cosA的值。
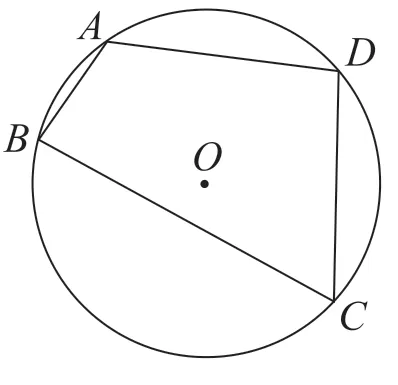
图5
(2)已知圆的内接四边形ABCD, 其 中,AB=a,BC=b,CD=c,DA=d,求cosA的值(用a,b,c,d表示)。
学生分析:连接BD,分别在△ABD和△BCD中利用余弦定理计算BD2,根据∠A与∠C互补,得到cosA=-cosC,两式相减即可得证。
这道题第一问由具体四边形出发,让学生探究。在前面例题的基础上,学生很容易想到分割四边形放到三角形中,再由之前的补角应用,很容易算出数值,在此过程中,学生分析问题的能力、数学运算素养得到进一步发展。第二问是新增内容,由特殊到一般,比较抽象,但在第一问铺垫的基础上,很容易发现还是分别在△ABD和△BCD中利用余弦定理计算BD2,根据∠A与∠C互补,得到cosA=-cosC,两式相减即可得证。这也是数学上常用的方法,特殊化探究出一般结论。
探究拓展2:教材105 页复习题探究拓展第10 题。
(1)如图6,在圆O的内接四边形ABCD中,AB=2,BC=6,CD=DA=4,求四边形ABCD的面积。

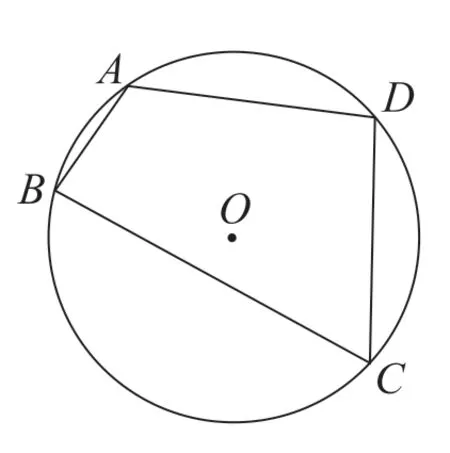
图6
这两道探究拓展题的题干是一样的,第二题是在第一题的基础上进一步深入探究,这两题的第二问也都是新教材中增加的,这也表明教材设计者在知识点巩固设计上的连续性和提高性,使学生的运算能力、思维能力得到进一步发展,让学生形成良好的思维品质。

合作探究:

四、运用互补角求解高考题
2021 年新高考Ⅰ卷19 题:记△ABC的内角A,B,C的对边分别为a,b,c。已知b2=ac,点D在边AC上,BDsin ∠ABC=asinC。
(1)证明:BD=b;
(2)若AD=2DC,求cos ∠ABC。

本文探究的互补角主要包括三类:一是一个大的三角形分成两个小的三角形后形成有公共边的两个互补角;二是平行四边形中的互补角;三是圆内接四边形中的对角互补。
