培养一年级学生数学思维能力例谈

佘海燕

摘要：培养学生的思维能力，是学生获取知识、发展智力和培养创新意识的重要途径。培养小学一年级学生的数学思维能力，需教师有意识、有计划、有步骤地对学生的思维进行训练，如“演用”直观教法，激活数学思维;“启用”语言功能，发展数学思维;“幻用”练习形式，深化数学思维。

关键词：

一年级学生  数学思维能力  培养  例谈

“学而不思则罔”。数学教育的根本就是培养学生的思维能力。小学一年级是教育的启蒙阶段，早期的思维训练是夯实思维发展的关键所需。因此，在教学实践活动中教师要有意识、有计划、有步骤地对学生的思维进行训练，以提高学生的思维能力。下面笔者就对学生数学思维能力培养的点滴做法阐述己见。

—、“演用”直观教法，激活数学思维

解决数学学科的抽象性与学生以具体形象思维为主的认知水平矛盾的重要手段，就是要多组织学生动手做一做，化抽象为直观，激活学生思维，进而迸发出思维的火花。

如教学一数（上）第100页的思考题，“我前面有9人，后面有5人，一共有多少人？”，此题有图有文，情节较为复杂，含有隐蔽条件，对小学一年级学生来说，理解起来确有一定的难度。许多学生本能地回答有14人，对此我没有急于评价，而是演示并指导学生根据题意先动手画一画，当形象、直观的图示被画出时，学生很快领悟到：要求总人数，不但要把“我”前、后的人数加起来，还要算上“我”自己，也就是“总人数=前面的人数+后面的人数+本人”。在面对接下来的一题“小朋友排队，从前数小红排第9个，从后数小红排第8个，这一队一共有多少人？”时，学生们主动在作业纸上画起了图，当一幅幅简洁的示意图被画出时，他们惊喜地发现了此题中所隐藏的“玄机”：从前数排第9个，从后数排第8个，实际就是小红前面有8个小朋友，后面有7个小朋友，同样可以用“总人数=前面的人数+后面的人数+本人”来计算。可见此处学生的动手“画”比老师的空口“说理”更有成效，它能变抽象为形象，较好地帮助学生完成由感性认识到理性认识的上升。

二、“启用”语言功能，发展数学思维

丰富数学语言系统，提高数学语言水平，对发展学生的数学思维有重要的意义。在平时的课堂教学中，我总是有意识地引导学生用数学文字语言来表达自己的发现或见解，鼓励他们多说。但初入学的一年级学生缺乏表达的方法和技巧，加之词汇量有限，在表达中往往会出现啰唆、词不达意等现象。当教学中每每出现此种情况时，我总会及时给予点拨、示范，为学生正确、完整、连贯的表达提供帮助。如在进行《8、7、6加几》的计算教学时，由于学生已有了前期“9加几”“8加几”的学习经验，并在学习过程中通过动手摆学具，对“凑十法”已有了较好地理解和认识，所以，在教学“7+4”时，我没有再让学生操作学具，而是让学生先想一想，然后直接用语言来叙述“凑十”的过程及计算方法。当学生东一句西一句，零零碎碎地叙述后，我适时引导：“你们能用‘可以……先……再……最后……这四个词将整个过程完整地说出来吗？”并将这个句式板书在黑板上。有了这个指引，学生略做思考后，争先恐后地举手回答：“可以把7凑成10，先将4分成3和1，再用7和3凑成10，最后10加1等于11;也可以把4凑成10，先将前面的7分成1和6，再用6和4凑成10，最后1加10等于11。”可想而知，当学生在完整叙述计算过程及方法时，他们脑中的思路是清晰的，对数与数之间的联系也是明确的，继而能抽象出计算过程，学生在观察、思考、表达的过程中，发展了抽象思维能力。

三、“幻用”練习形式，深化数学思维

练习，不仅可以帮助学生加深对基础知识的理解，而且能促使思维深化。

在教学过程中，教师要抓住练习环节，设计、变幻多种“练”的形式，通过“一题多问”“一题多变”“一题多法”等活动来提升学生的数学思维。

“一题多问”是根据题中给出的信息，引导学生展开联想，提出尽可能多的问题，以此来激活学生的思维，并朝着纵深方向发展。如：根据“班级大扫除，小刚擦了12张课桌，小新擦了9张课桌”这些信息，引导学生提出不同的问题。开始学生只提出了他俩一共擦了多少张课桌，我适时启发，能不能从他们所擦的课桌数量间的关系再想想，学生积极思考，陆续又提出了小刚比小新多擦了几张课桌？小新比小刚少擦了几张课桌？这时教室安静了下来，同学们都认为不能提出其他问题了，我再次启发学生结合直观示意图，从已知信息的深度和广度去探索，学生受到启发又相继提出了小新再擦几张桌子就和小刚擦得同样多了？小刚少擦几张桌子就和小新擦得同样多？这样的提问练习不仅丰富了学生对加、减法现实意义的认识，而且对学生思维的敏捷性、深刻性进行了锻炼，也凸显了课标中要求的“因材施教”。

“一题多变”是指一题解答完毕后，通过对题设、结论的改变引申新问题，让学生融会贯通知识间的联系，从而做到举一反三，触类旁通。如教学教材一数（上）第94页的思考题。

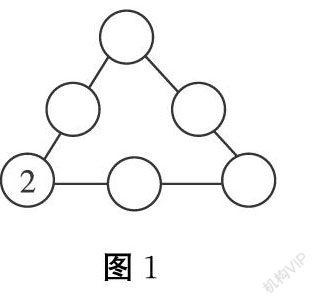
原题：在○里分别填上3、4、5、6、7，使每条线上的三个数相加都得12。（见图1）

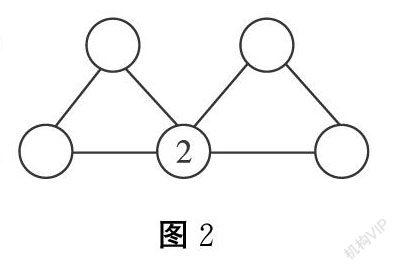
当学生通过阅读信息进行分析思考，最后得出结论：只要和2在一条线上的两个数相加的得数是10就行了，所以2和7、3在同一条线上，和6、4也在同一条线上，剩下的一条线就是3、5、4。为了巩固学习效果，将原题为：从3、4、5、6、7里选择合适的数填入○里，使两个三角上的三个数相加的和相等。（见右图2）

由原题每条线上的三个数变为每个三角上的三个数，看似变化不大，甚而觉得较原题还简单些，其实此题有一定的深度——每个三角上三个数相加之和没有直接告知且有众多个答案。学生有了之前的基础，再通过多方质疑、推理，很快发现：只要使最左边斜线上的两个数的和等于最右边斜线上的两个数的和，则可解决此题。因为3+6=4+5，3+7=4+6，4+7=5+6，所以这题有三种不同的答案。此练习形式不仅锻炼了学生思维的灵活性、流畅性，而且使学生分析问题、解决问题的能力得到了提高。

“一题多法”就是启发学生从不同的方向和角度去审视、分析数学问题，寻求多种解决方法，以此培养学生思维的求异性、变通性。如在教学“解决问题”时，教师出示情境图：左边7个梨（其中3个小卡通梨，2个大普通梨，2个小普通梨），右边5个梨（1个卡通大梨，3个普通大梨，1个普通小梨），求一共有多少个梨？此题教师引导学生从不同角度提取信息（①左边7个梨，右边5个梨②6个大梨，6个小梨③4个卡通梨，8个普通梨），得到多种解答方法，不仅扩展了学生的解题思路，同时也加深学生对所学知识的理解，有效促使学生开动脑筋，打破“左右相加”的思维定式，培养学生从多角度观察、思考问题的能力，锻炼了学生数学思维的发散性，为创新思维的培养打下基础。

总之，在教学中培养一年级小学生数学思维能力，教师要抓住直观教学契机，鼓励学生多动手操作;营造宽松语言环境，示范、引导学生多动口表达;设计灵活多变练习形式，促使学生多动脑思考，再给以正确的学习方法指导，学生的数学思维能力必将得到有效发展，并终将成为学生今后“乘风破浪”的有力保障。

参考文献：

[1]董仕超、李建军.浅谈怎样培养小学一年级学生数学思维能力[J].未来英才，2016（10）.

[2]祖秀娟.抓住数学之魂 培养发散性思维——小学数学发散性思维的培养方法[J].课程教育研究，2019（17）：169.

[3]沈秋红.有序思考 深度发展——例谈人教版一上教材中的一道思考题[J].小学数学教师.2019（11）.

[4]王佳哲.论思维与语言的关系[J].北方文学.2019.