某对数周期天线结构优化设计与力学分析

2021-08-30李东颖贺奎尚孔令兵孙瑞峰刘良玉

航天制造技术 2021年4期

李东颖贺奎尚孔令兵孙瑞峰刘良玉

某对数周期天线结构优化设计与力学分析

李东颖贺奎尚孔令兵孙瑞峰刘良玉

（上海航天电子技术研究所，上海 201109）

介绍了一种UHF波段的对数周期天线的结构优化设计。为了提高天线的整体刚度，使用张紧绳索优化天线结构。采用有限元方法分别对无绳索、张紧绳索加固的两种对数周期天线结构进行模态分析，结果发现，采用张紧绳索加固的天线结构刚度有了大幅度提升。通过计算得到了张紧绳索加固的天线结构在低量级振动条件下的加速度响应，并通过低量级振动试验进行了验证，证明了结构优化设计的合理性，为后续组合馈源阵的设计奠定了基础。

对数周期；结构优化；张紧绳索；有限元；振动试验

1 引言

对数周期天线是一种宽带定向天线[1]，具有频带宽、结构简单、造价便宜、质量轻、容易控制极化、有一定的波束宽度和增益等优点[2，3]，在短波、超短波直至微波等低波段的侦察、测向、通信、电子对抗等方面有着广泛应用。

对数周期天线是由几个不同长度和位置的偶极子振子[4，5]构成，如图1所示。

在实际的应用中，经常将对数周期天线按一定角度组阵，这种方法能够扩宽天线有效频率范围，提高天线增益，获得更高的功率。

本文以某UHF波段的对数周期天线单元为研究对象，对其进行了结构优化设计，采用绳索张紧的方式加固天线整体结构，使用有限元方法分析了天线结构加固前、加固后的结构动力学特性，并通过低量级振动试验验证了结构优化后的仿真结果，为后续组合馈源阵的进一步设计奠定了基础。

图1 典型对数周期天线

2 天线结构设计及优化

对数周期天线单元主要结构为4个树状辐射片、辐射环、底部支座及4个十字支撑骨架、部分紧固件组成，如图2所示。

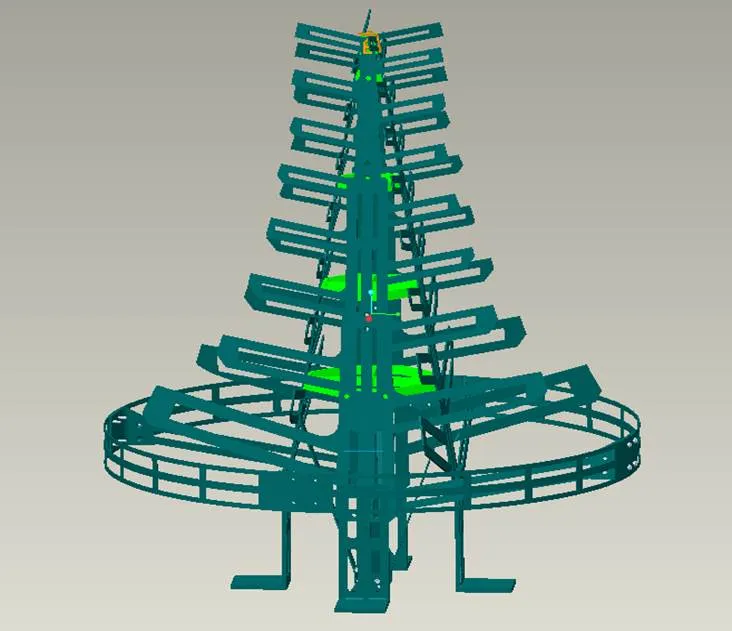
图2 对数周期天线结构

由图2可以看出，对数周期天线单元中整体结构相对离散，尤其是树状辐射片及辐射环的局部模态较多，又为了减轻天线单元的重量，通过张紧的柔性绳索代替紧固件，对辐射环加以支撑，并对离散的树状辐射片施加约束，使对数周期天线加固为一个整体的结构，保证其满足力学试验环境。采用柔性绳索约束的天线模型如图3所示。

图3 张紧绳索加固对数周期天线结构

3 有限元建模

建立对数周期天线有限元模型。由于天线树状辐射片、辐射环、十字支撑骨架及紧固件均为薄片结构，故采用壳单元模拟，约束辐射环及根部辐射片的张紧绳索采用梁单元模拟，其中，树状辐射片、辐射环、底部支座采用铝合金材料，十字支撑骨架采用玻璃钢材料，紧固件质量均布在天线结构上。材料性能参数如表1所示。

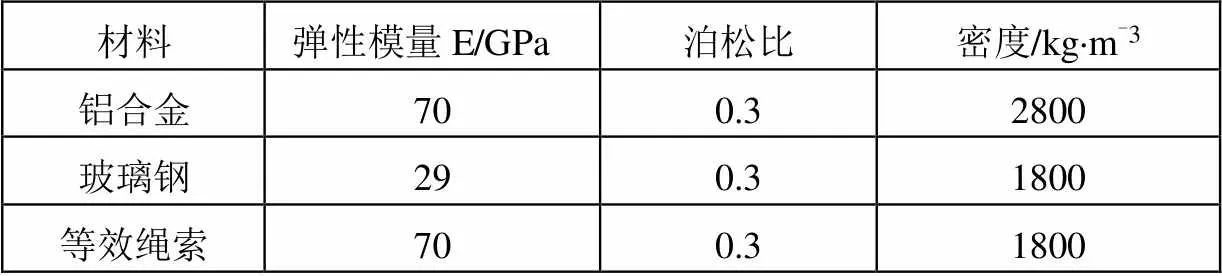
表1 材料性能参数

采用RBE2多点约束单元模拟不同组件之间的连接方式，天线最底部支座及辐射环支撑绳索底部为固定约束。分别建立无绳索及张紧绳索加固后的对数周期天线有限元模型，如图4、图5所示。

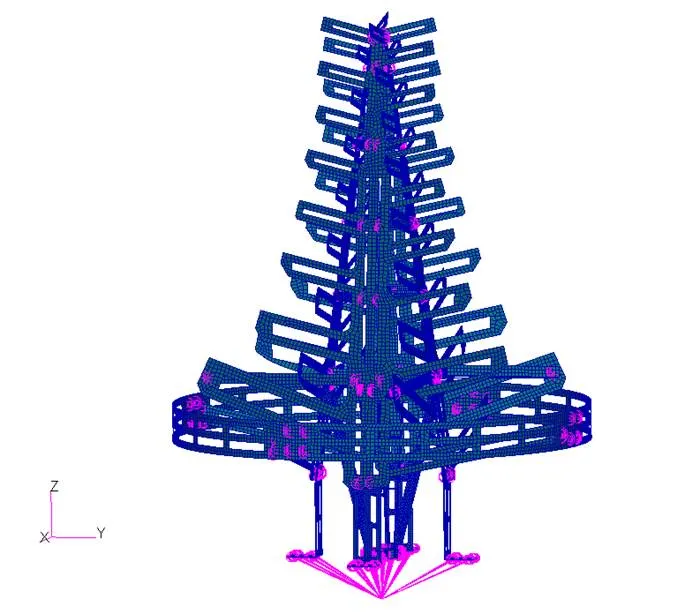
图4 无绳索的对数周期天线有限元模型

图5 张紧绳索对数周期天线有限元模型

4 模态分析

4.1 无阻尼自由振动微分方程

对数周期天线结构属于典型的多自由度振动系统，其结构动力学特性包括固有频率和振型，可利用多自由度振动理论对其进行理论分析[6～8]。实际分析时，将天线结构简化为一个自由度集中参数系统，即取前阶模态频率值和振型。多自由度系统的自由振动方程一般为：

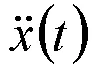
化系统阻尼，式（1）可简化为：

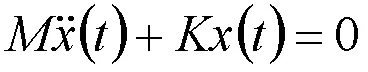
系统的自有振动一般为简谐振动，其位移矢量为：

式中，为振幅矢量，为振动频率。将式（3）带入式（2），得到系统的振型方程：

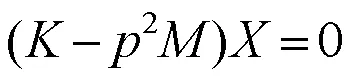
式（4）为齐次线性方程组，其具有非零解的充分必要条件为系数矩阵行列式为零，即满足：

4.2 无绳索的对数周期天线结构模态计算

计算得到无绳索的对数周期天线结构的前3阶模态频率值分别为14.96Hz、24.46Hz、25Hz。前3阶振型如图6～8所示。

图6 无绳索的对数周期天线结构的1阶振型

图7 无绳索的对数周期天线结构的2阶振型

图8 无绳索的对数周期天线结构的3阶振型

由振型图可知，天线前3阶频率均为辐射环的局部模态。

4.3 张紧绳索加固的对数周期天线结构模态计算

计算得到张紧绳索加固的对数周期天线结构的前3阶模态频率值分别为51.35Hz、51.53Hz、72.79Hz。前3阶振型如下图9～11所示。

图9 张紧绳索加固的对数周期天线结构的1阶振型

图10 张紧绳索加固的对数周期天线结构的2阶振型

图11 张紧绳索加固的对数周期天线结构的3阶振型

由振型图可知，对数周期天线第1阶振型为向平动；第2阶振型为向平动；第3阶振型为向旋转。

通过无绳索及张紧绳索加固的两种对数周期天线结构的模态计算结果可知，经结构优化后，天线的基频从14.96Hz提高到51.35Hz，结构刚度得到了大幅度提高。

5 低量级振动频率响应分析

在张紧绳索加固的对数周期天线有限元模型约束节点向施加0.2g（5～100Hz）的低量级振动条件，采用Nastran有限元软件计算得到图5测点位置处的加速度响应，如图12所示，测点位置的最大加速度响应为52Hz/4.35g。

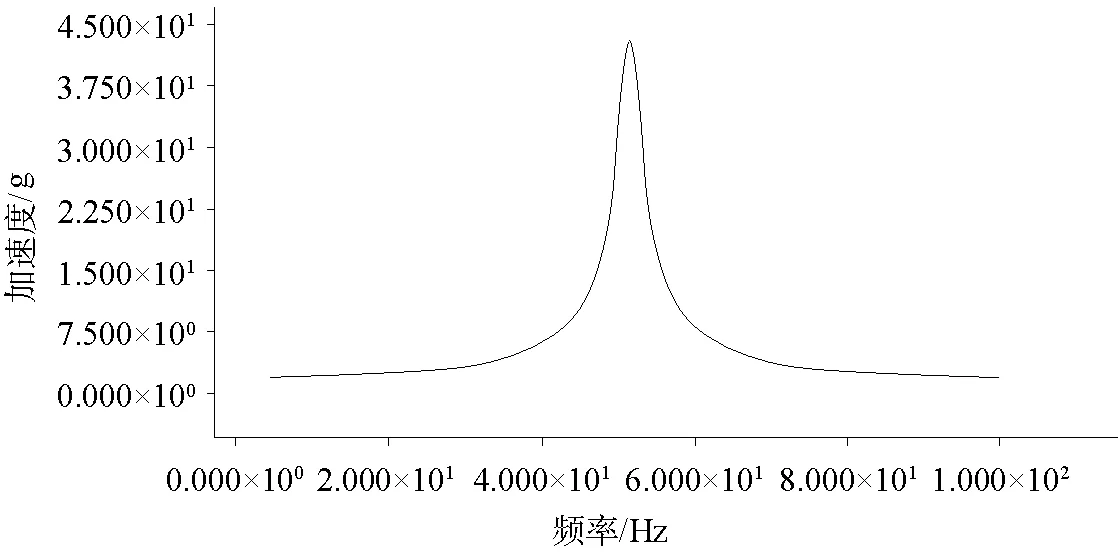
图12 加速度响应

6 低量级振动试验

为了验证对数周期天线结构设计的合理性，对张紧绳索加固的对数周期天线进行向低量级振动试验。通过低量级振动试验，可以得到结构的共振频率，也可以得到测量点的加速度响应。试验状态如图13所示，测量点位置如图14所示。在试验过程中，天线底座及辐射环张紧绳索底部通过螺栓固定在工装上，工装直接与处于水平状态的振动台相连。

图13 天线振动试验状态

图14 响应测量点

采用0.2g（5～100Hz）的低量级振动条件对天线进行向激励，通过低量级扫描，即可得到结构的共振频率，也可以得到加速度响应。向（横向）低量级扫描响应曲线如图15所示。

图15 加速度响应

由低量级振动试验响应可知天线向的最大加速度响应为55.7Hz/4.25g，与第5章天线低量级振动计算得到的频率误差为7.1%，加速度响应误差为2.3%，结果吻合较好，验证了对数周期天线有限元计算的准确性及结构设计的合理性。

7 结束语

对一种UHF波段的对数周期天线进行了结构优化设计。采用张紧绳索优化天线结构，并进行动力学分析，结果标明，结构优化后，天线具有更高的刚度。计算得到结构优化后的天线低量级振动响应，并通过低量级振动试验验证了计算结果，结果吻合较好，证明了对数周期天线结构优化的合理性，并为后续组合馈源阵的进一步设计提供了验证和依据。

1 Carre L. The Design of Log-Periodic Dipole Antennas [G]. 1961 IRE International Convention Record, 61～75

2 Cheong W M, King R W P. Arrays of unequal and unequally spaced dipole [J]. Rad Sci, 1967, 2(11): 1303～1314

3 Cheong W M, King R W P. Lop-periodic dipole antenna [J]. Rad Sci, 1967, 2(11): 1315～1325

4 朱丹丹. 天线阵列优化研究[D]. 武汉：华中科技大学，2006

5 Larricoals P J B. Propagation and antennas for mobile communications [S].London Institution of Electrical Engineers, 2003

6 张洪才. ANSYS 14.0理论解析与工程应用实例[M]. 北京：机械工业出版社，2013

7 刘鸽. 机载信息处理机结构仿真分析与关键技术研究[D]. 西安：西安电子科技大学，2006

8 张翼，黄春江. 某碳纤维电子机箱结构动力学仿真及试验研究[J]. 电子机械工程，2020，36(4)：26～31

Structure Optimization and Mechanical Analysis of A Log-Periodic Antenna

Li Dongying He Kuishang Kong Lingbing Sun Ruifeng Liu Liangyu

(Shanghai Aerospace Electronic Technology Institute, Shanghai 201109)

The structure optimization of a log-periodic antenna in UHF wave is introduced. To improve the holistic stiffness of the antenna, the structure is optimized by tension ropes. The modal analysis of two kinds of log-periodic antenna structures without rope and with tension ropes is carried out. The results show that the stiffness of the antenna structure strengthened by tension ropes has been greatly improved. The low-grade vibrate acceleration response of the antenna structure strengthened by tension ropes is analyzed and verified by low-grade vibration test, which provide the rationality of the structure optimization design and lay basis for follow-up combined design.

log-periodic；structure optimization；tension ropes；FEM；vibration test