改进蚁群算法在生产线加工方案选择中的应用

孔志学 姜 恒 张珠峰

改进蚁群算法在生产线加工方案选择中的应用

孔志学 姜 恒 张珠峰

（上海航天精密机械研究所，上海 201600）

针对多品种小批量数控加工生产线，不同工件、多种工艺路线在同一条生产线上进行混合生产时生产线节拍低、设备利用率低的问题，提出了一种迭代渐进式蚁群算法对生产线最优加工方案进行选择。基于时序优先原则，按工艺路线串行、设备资源使用时间连续的准则，建立生产线时间模型及生产线综合评价指标；改进算法流程，限定初代算法规模，快速遍历所有产品加工路线，再逐步扩大算法规模，根据历代最优解不同工艺路线分布情况，对蚂蚁路径距离值进行更新，采用至今最优蚂蚁信息素叠加扩散策略，促使搜索进程加速向最优解收敛；采用低阈值伪随机算法，提高算法全局搜索能力，避免算法后期陷入局部最优解。在VS2015软件平台上进行算法仿真对比，结果表明，该算法在避免局别最优和算法收敛速度方面具有明显优势。

生产线时间模型；迭代渐进式蚁群算法；时间线排序；工艺路线

1 引言

近年来，随着航天事业的快速发展，航天典型结构件数控加工生产线不断投入生产应用，而航天产品依然以多品种中小批量生产为主，用于生产单一产品的加工生产线运行效率低、设备利用率低、投资成本高，已成为制约生产线相关技术在航天企业推广应用的瓶颈之一。

为提高流水车间的生产效率和设备利用率，Liu Yencheng等[1]提出一种流水车间作业模型，将工件不同类型，设计分支定界算法，优化降低车间生产周期；段建国等[2]提出了一种基于时间向量的多工序加工系统工艺路线重组建模与优化方法，提高了工艺规划的柔性和动态适应性。Liu Jiyin等[3]建立了混合整数线性规划模型，以解决工艺重入和并行工作站的周期性调度问题；孔继利等[4]提出了一种平顺移动模式下考虑加工时间与调整时间可分离的多目标流水车间批量调度方法，基于禁忌搜索算法求解最优调度方案，并实现为批量工件的加工和加工制造设备调整指定精确的生产作业计划。

生产线是考虑物流资源条件下有限加工设备流水线式制造的生产系统，具有柔性制造、并行制造的特点，对生产节拍、设备利用率要求苛刻。谢尧等[5]提出了面向零件加工的并联柔性生产线排产与调度系统，采用粒子群算法解决了生产线指定机床加工、紧急插单、超期时间最短等需求的算法优化问题；毛永年[6]等提出具有并行制造特征的自动化混流生产线调度（MILP）模型，优化了制造系统的生产效率；而刘伟等[7]则构造了加工工艺顺序模型，并运用蚁群算法对工艺路线进行了优化；常智勇等[8]提出一种自适应蚁群算法，将生产资源对产品工艺路线的选择考虑在内，以制造资源更换率最小为目标，实现了制造条件约束下的产品最优工艺路线选择；邓可等[9]提出基于蚁群算法的半导体生产线调度模型（ASWFSM），引入专家系统作为推理机，在小规模生产线调度问题上具有良好的效果和稳定性；杨煜俊等[10]提出的混合蚁群算法，在解决机器人多任务作业调度问题上，具有较高的可靠性和鲁棒性。可见，生产车间、生产线的排产与调度优化是一个重要的研究课题，蚁群算法及其改进算法在该研究领域取得了较好的效果。

本文针对不同工件、多种工艺路线在同一条生产线混合生产时的工艺路线寻优问题，提出迭代渐进式蚁群算法，在建立生产线时间模型与生产线综合评价指标的基础上，通过改进蚁群算法，在迭代过程中更新路径距离值，并引入至今最优蚂蚁信息素叠加扩散策略、低阈值伪随机算法，提升了蚁群算法的性能。

2 生产线时间模型构建

以多品种中小批量生产线为研究对象，针对不同工件、不同工艺路线在生产线上进行混合生产，基于时序优先原则，按工艺路线串行、设备资源使用时间连续的准则，建立生产线时间模型。

2.1 工艺路线模型构建

面向生产线的工艺路线是对产品毛坯在生产线上加工制造成为零件的过程的描述，而工艺路线是工序的集合，因此，可将工序相关的加工信息定义为产品的工序MP（manufacturing process），使用七元组表示：

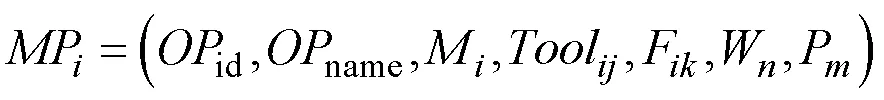
其中，id为工序编码，name为工序名称，M为生产线使用机床的集合，Tool为不同设备资源使用刀具的集｛Tool1,Tool2,...,Tool｝合、F为不同设备资源使用工装的集合｛F1,2,...,F｝、W为不同设备资源使用方法的集合｛1,2,...,W｝、P表示不同状态下的零件。由零件各工序所组成的集合即为该零件的工艺路线PR（Process Route），表示如下：

2.2 约束条件

本文构建的时间模型和算法具有以下约束条件：

a. 生产线中的设备资源在生产线运行过程中不发生故障；

b. 生产线中的数控机床在同一时间只能加工一个工件的某一道工序，且每个工件每道工序只能指定一台数控机床，若该工序有可替代机床，则按新工艺路线进行配置；

c. 每道工序包括上料、加工、下料等三个环节，若有测量机，则按数控机床加工处理；

d. 每道工序完成的标志是下料完成；

e. 后道工序必须在前道工序完成后，才能被加工；

f. 生产线中的设备资源同一时刻只能执行一项生产任务；

g. 同一设备资源不同任务，按任务时序优先的原则进行顺序排列，时间重叠的低优先级任务向后顺延。

2.3 生产线时间模型设计

无故障条件下的生产线连续运行是各个设备不同任务的组合，将生产线的各类任务抽象为时间片段，则生产线时间模型是对各个任务执行时间片段及时间片段间时序关系的描述。如图1所示，可知，根据上述工艺路线模型，针对不同产品，可设置多种工艺路线，但对生产线系统而言，不同工艺路线、不同工序可使用的设备资源是一定的，各个设备上下料所使用的机器人或其他物流设备及其备料或存料的辅助装置是一定的。

图1 产品工艺路线与生产线资源对应关系图

本文针对生产线系统，基于VC++分别设计了相应的单向链表对象用以描述产品工艺路线的时间模型、加工设备的时间模型、物流系统的时间模型。

b. 产品工艺路线时间对象

定义工序为物流系统上料load、机床加工machining、物流系统下料unload等时间片段的组合对象，则工艺路线可描述为组成工艺路线的所有工序单向链表对象的集合。

2.4 基于时间模型的生产线综合评价指标

流水车间调度问题的决策目标一般为时间资源[11]，本文考虑采用生产线生产节拍以及设备利用率作为生产线综合评价指标对工艺路线及其时序进行优选，并对应设置权重系数，目标函数如下：

其中，为生产线设备加工任务总数量，为生产线加工产品总数量，为单一产品的工序数量，target为生产线评价的生产节拍目标值，target为机床设备利用率目标值，为权重系数。

3 经典蚁群算法

经典蚁群算法是一种模拟蚂蚁群觅食过程寻求最短路径的群体智能算法[12]，蚁群随机选择路径，并在每条路径上留下信息素，信息素随时间不断挥发，使蚁群能够按信息素浓度高的路径选择最短路径。本文将生产线加工产品数量与TSP问题中的城市数量对应，路径的选择与工艺路线的选择对应，路径最大距离与生产线综合评价指标相对应，基于经典蚁群算法对生产线工艺路线进行了优选。

3.1 概率函数

蚁群在选择工艺路线时，其转移概率根据信息素浓度与启发式函数确定[13]，本文采用轮盘赌法保证算法的搜索能力，状态转移概率由式（2）～式（4）确定：

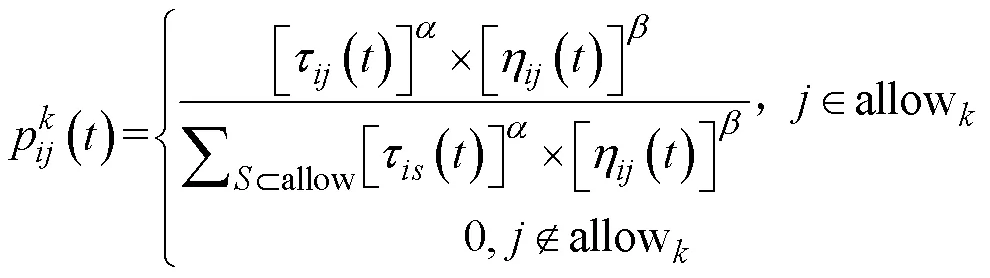
3.2 生产线时间线排序

基于上述约束条件，分别建立生产线加工时间模型、机床时间模型、机器人时间模型，并按以下步骤排序，如图2所示。

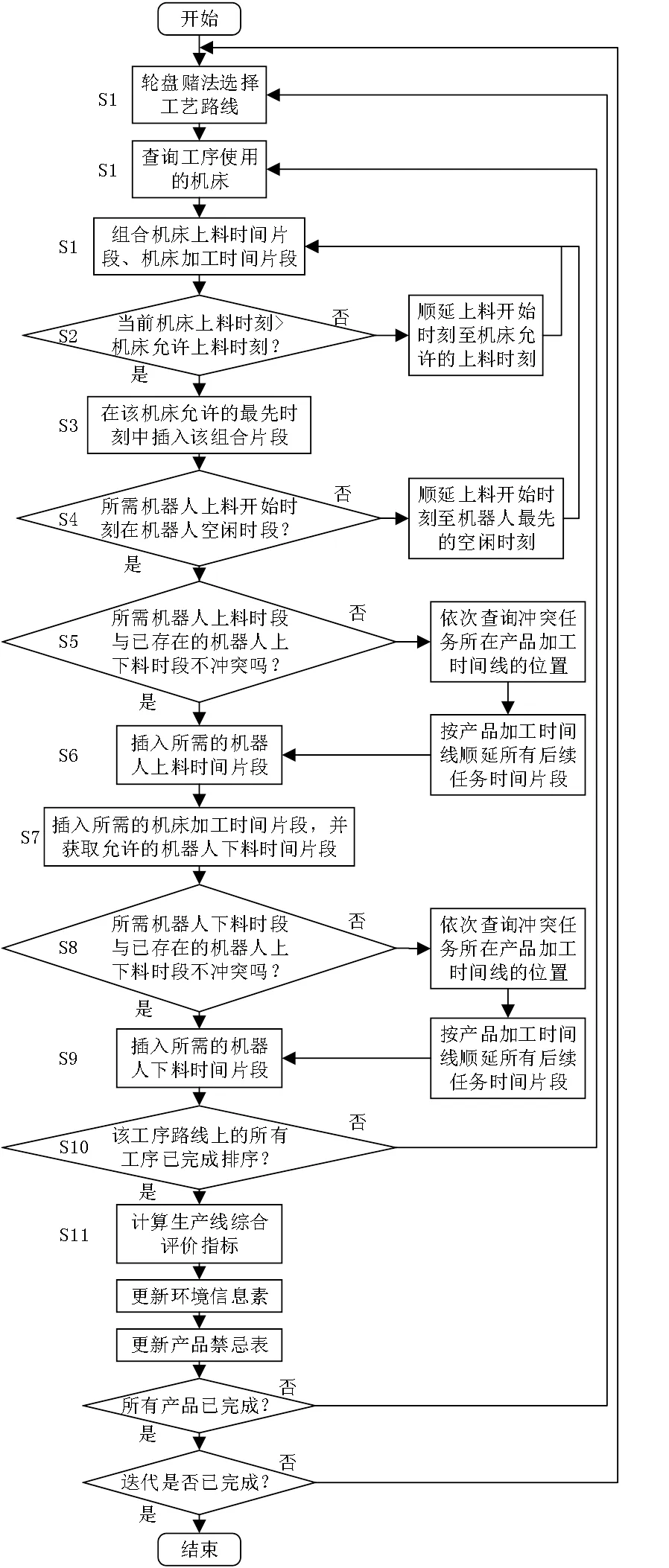
图2 经典蚁群算法流程图

S1：首先在工艺路线选取后，按集合顺序查询工序对象，并根据工序设置的机床组合所需机器人上料时间片段和该机床加工时间片段。

S2：判断该机床所需的上料时刻是否属于该机床当前时间线中的允许上料时间段内，若与已存在的机床任务冲突，则顺延至最先的允许上料时刻。

S3：将S1的组合时间片段插入该机床时间模型链表对象中。

S4：判断机床所需的机器人上料时间片段是否在机器人空闲时段，若不在空闲时段，则顺延该机床上料开始时刻至机器人最先的空闲时刻，并返回S1。

S5：判断该时间片段是否与已存在的机器人上下料任务有冲突，若有冲突，则先定位冲突任务的时间片段所在生产线时间模型的位置，再按生产线时间模型，顺延冲突任务及其后续任务的时间片段。

S6：将机器人上料时间片段插入机器人时间模型、生产线时间模型中。

S7：将机床加工时间片段插入机床时间模型、生产线时间模型中，并获取该机床所需的机器人下料时间片段。

S8：判断该机器人下料时间片段是否与已存在的机器人上下料任务有冲突，若有冲突，则先定位冲突任务的时间片段所在生产线时间模型的位置，再按生产线时间模型，顺延冲突任务及其后续任务的时间片段。

S9：将机器人下料时间片段插入机器人时间模型、生产线时间模型中。

S10：判断工艺路线是否已结束，若未结束，返回S1直至结束。

S11：根据生产线时间模型、机床时间模型的链表对象计算生产线综合评价指标。

3.3 信息素更新

按信息素规则要求，在蚂蚁释放信息素的同时，对路径上的信息素按比例挥发，并按式（5）～式（7）更新。

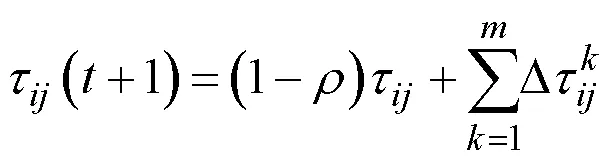
4 迭代渐进式改进蚁群算法

结合数控加工生产线批量生产的特点以及生产组织经验，多品种中小批量混线生产时，某一产品上线生产一般采用单一工艺路线生产线效率较高，提出了一种迭代渐进式改进蚁群算法。

4.1 不同批量条件下的最优方案对比

首先基于经典蚁群算法对不同批量条件下生产线最优加工方案进行优选与对比，软件仿真试验条件及结果如表1所示。

表1 不同批量下的产品工艺路线执行情况表

如图3所示，不同批量条件下，产品在生产线加工的最优加工方案中，工艺路线的分布具有明显规律。其一，在单一批量条件下，A产品一般以工艺路线1、工艺路线2为主，B产品一般以工艺路线1为主；其二，在不同批量间，产品工艺路线的分布区间占比具有一致性，且批量越大，越明显。

图3 不同批量条件下各工艺路线分布情况图

4.2 算法流程改进

本文提出的迭代渐进式改进蚁群算法流程如图4所示。

图4 迭代渐进式改进蚁群算法流程图

S1：根据上线加工的产品种类及其适用的生产线工艺路线数量，确定每代产品的加工数量，按式（8）～式（10）更新。

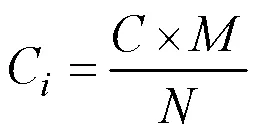
式中，为上线产品总数量，为上线产品种类数，M为第中产品工艺路线数，为所有产品工艺路线的总数，n为第代时产品加工数量，C为第代蚁群迭代的次数，为蚁群算法的总迭代次数。

S2：按轮盘赌法进行工艺路线选择，并依次对工序路线中的工序进行时间排序，计算生产线综合评价指标，更新环境信息素，更新产品禁忌表。

S3：迭代完成生产线最优工艺路线选择。

S4：按式（11）更新距离矩阵。

式中，X为第个工艺路线在最优工艺路线中被选择的次数。

S5：若所有产品已完成加工，则结束，否则，返回S1。

4.3 算法参数优化

经典蚁群算法存在易陷入局部最优、收敛速度慢的问题，蚁群系统ACS、精英策略蚁群算法ASelite[14]、最大最小蚁群算法MMAS[15]等均在不同应用案例中可对算法性能在一定程度上进行改进，参考前期的研究成果，引入精英蚂蚁策略和伪随机比例规则对信息素更新和轮盘赌法优化。

改进式（5），按式（12）、式（13）更新。

对轮盘赌法改进，采用伪随机比例规则，状态转移概率按式（14）更新。

5 结果与分析

本文使用VS2015平台，将迭代渐进式蚁群算法与经典蚁群算法AS、蚁群系统算法ACS、精英蚁群算法ASelite、最大最小蚁群算法MMAS进行软件仿真与对比分析。

5.1 应用对象

如图5所示，舱体生产线包括2台车铣复合加工中心、3台卧式五轴加工中心、1台桁架机器人、1台地轨机器人，两种典型产品：舵机舱、电子舱，适用于生产线的产品工艺路线分别为3种、2种，每组批各8件。

图5 舱体生产线组成图

5.2 参数设置

两种产品各工艺路线条件下实际工序时间及机器人上下料时间条件如表2所示。

表2 产品工艺信息表 s

生产线综合评价指标优化计算时，生产节拍、设备利用率目标值分别为target=3h/件，target=60％，权重系数=0.7。

5.3 仿真对比

五种算法仿真对比试验中，至今最优解及其进化迭代次数如表3所示。可见，本文提出的算法在寻优能力优于AS、ACS、ASelite、MMAS算法；在最优解选取上，明显优于AS算法最优解的值，与ACS、MMAS算法最优解的值接近，与ASelite算法最优解的值基本一致。

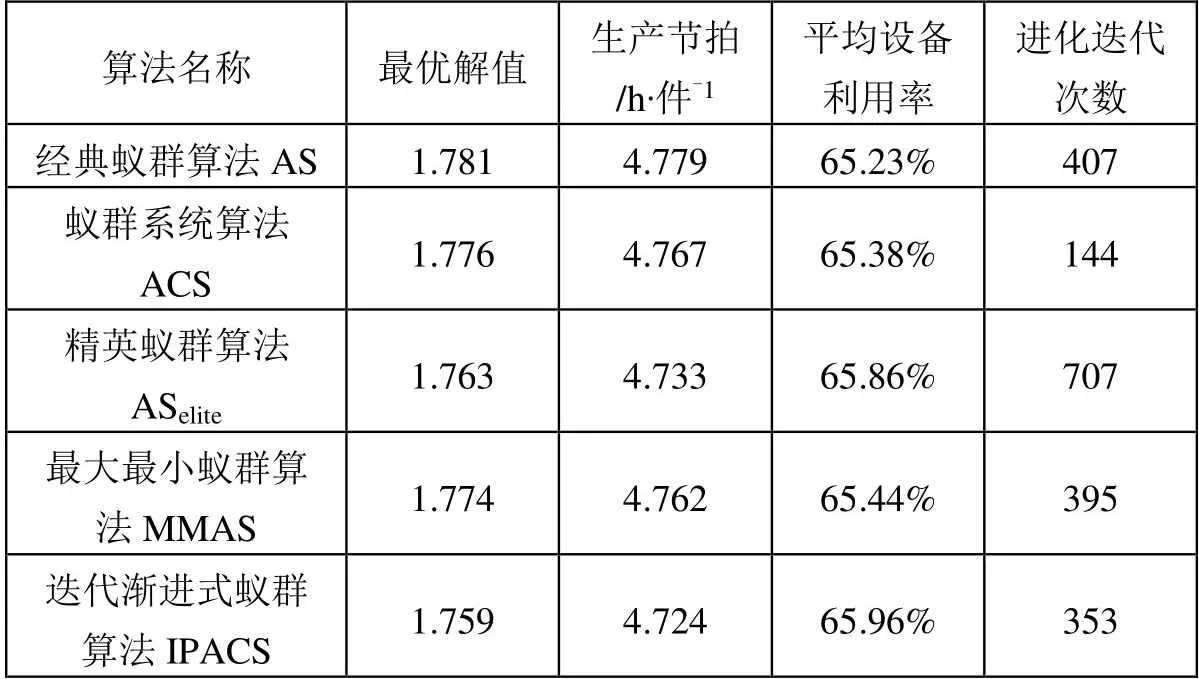
表3 五种算法对比试验数据统计表

五种算法的历代最优解收敛趋势图如图6所示。可见，本文提出的算法在初期收敛速度上与其他四种算法相近；在中期保持了一定的发散性，在后期，仍然具有一定的全局检索能力。

图6 历代最优解收敛趋势图

五种算法仿真对比试验中，IPACS、ASelite算法最终获得的生产线最优加工方案一致性较好，如图7所示，为本文提出算法最优解条件下，生产线选择五种路线的时序及五台机床的上料、加工、下料的时间片段分布图，可见，该算法对两种产品五种工艺路线的加工时序进行了合理排序，使五台机床加工任务的时间片段较为连续，生产线总体生产节拍最小，机床设备平均利用率最高。

图7 生产线最优加工方案时序图

因此，本文提出的迭代渐进式蚁群算法在收敛能力上与主流改进蚁群算法相当，在寻优能力、避免陷入局部最优解等方面具有优势。

6 结束语

针对数控加工生产线加工方案优选问题，提出了一种迭代渐进式蚁群算法，改进后的算法在收敛速度、寻优能力具有明显优势。本文算法具有以下特点：

a. 改进算法流程，在小规模算法条件下，获取工艺路线分布情况，并迭代更新路径距离，提高算法中后期选择较优工艺路线的概率，提高收敛速度。

b. 引入至今最优蚂蚁信息素叠加扩散策略，提高算法向全局最优解收敛的能力。

c. 采用低阈值伪随机算法，提高算法后期的全局搜索能力，避免提前陷入局部最优。

1 Liu Yencheng, Fang Kueitang, Lin B M T. A branch-and-bound algorithm for make span minimization in differentiation flow shops[J]. Engineering Optimization, 2013, 45(12): 1397～1408

2 段建国，王彦森，谢楠. 基于时间向量的多工序加工系统工艺路线重组建模与优化[J]. 计算机集成制造系统，2020，26(7)：1814～1823

3 Liu Jiyin, Jiang Yun, Zhou Zhili. Cyclic scheduling of a single hoist in extended electroplating lines: a comprehensive integer programming solution[J]. IIE Transactions, 2002, 34(10): 905～914

4 孔继利，苑春荟，杨福兴，等. 平顺移动模式下考虑加工时间与调整时间可分离的多目标流水车间批量调度[J]. 系统工程理论与实践，2017，37(11)：2882～2896

5 谢尧. 面向零件加工的并联柔性生产线排产与调度系统研发[D]. 武汉：华中科技大学，2018

6 毛永年，唐秋华，张利平，等. 具有并行制造特征的自动化混流生产线调度模型[J]. 计算机集成制造系统，2019，25(7)：1717～1728

7 刘伟，王太勇，周明，等. 基于蚁群算法的工艺路线生成及优化[J]. 计算机集成制造系统，2010，16(7)：1378～1382

8 常智勇，杨建新，赵杰，等. 基于自适应蚁群算法的工艺路线优化[J]. 机械工程学报，2012，48(9)：163～169

9 邓可，林杰，张鹏. 基于蚁群算法的半导体生产线调度方法研究[J]. 计算机工程与应用，2009，45(12)：198～201

10 杨煜俊，陈业. 求解柔性机器人车间调度问题的混合蚁群算法[J]. 计算机工程与应用，2018，54(13)：160～167

11 Yenisey M M, Yagmahan B. Multi-objective permutation flow shop scheduling problem: Literature review, classification and current trends[J]. Omega, 2014, 45(2): 119～135

12 王凤，林杰. 设备组合加工的生产调度问题研究[J]. 计算机工程与应用，2009，45(11)：26～29

13 刘中强，游晓明，刘升. 一种启发式动态信息素更新策略的蚁群算法[J]. 计算机工程与应用，2018，54(20)：20～27

14 汪贵庆，袁杰，沈庆宏. 基于精英蚁群算法的交通最优路径研究[J]. 南京大学学报（自然科学版），2019，55(5)：709～717

15 杨延庆，李鹏飞，何博. 求解TSP问题的改进最大最小蚁群算法[J]. 西安工程大学学报，2010，24(6)：818～821

Application of Improved Ant Colony Optimization in Production Line Processing Planning

Kong Zhixue Jiang Heng Zhang Zhufeng

(Shanghai Spaceflight Precision Machinery Institute, Shanghai 201600)

In order to solve the problems of low production cycle and low equipment utilization when different workpieces with multiple process routes are processed on the multi-variety and small batch CNC machining production line, an iterative progressive ant colony algorithm is proposed to select the optimal processing plan of the production line. Based on the principle of time sequence priority, the process route serialization and equipment resource usage time continuous criteria, establish production line time model and production line comprehensive evaluation index; improve the algorithm process, first, limit the scale of the first generation algorithm, quickly traverse all product processing routes, and then gradually expand the algorithm scale. According to the distribution of different process routes of the best solutions in the past generations, update the ant path distance value, adopting the best ant pheromone superposition diffusion strategy so far, to promote the search process to accelerate the convergence to the optimal solution; using a low-threshold pseudo-random algorithm to improve the algorithm’s global search ability and avoid the algorithm from falling into the local optimal solution in the later stage. On the VS2015 software platform, the algorithm simulation comparison is conducted. The results show that the algorithm has great improvement in avoiding local optimization and accelerating convergence speed.

production line time model；iterative progressive ant colony system；timeline sort；process route

TP274

A

孔志学（1989），硕士，机械工程专业；研究方向：数字化生产线技术。

2021-07-09