基于欧氏距离变换的无人机图像拼接*

王鹏钊，陈宇哲，潘斐扬

（电子科技大学，四川 成都 611731）

0 引言

无人机技术在现代社会中有广泛的应用，由无人机拍摄的航拍图像可以较为清晰地显示出自然地貌、地面建筑和交通线路等关键地理特征。无人机凭借着其灵活性高、可操作性强等特征，在地图绘制、灾害防治以及军事侦察方面有着重要的应用[1]。然而现阶段大部分无人机都很难直接在高空通过单次拍摄获得某一区域的全景图像，因此低空拍摄多组图片再通过计算机处理、拼接、融合得到一张大图的方式逐渐成为当下无人机航拍的主流。

常用于无人机图像拼接的特征匹配算法有尺度不变特征变换匹配算法（Scale Invariant Feature Transform，SIFT）、加速鲁棒特征（Speeded Up Robust Features，SURF）以及定向加速测试特征和旋转二值鲁棒独立基本特征（Oriented FAST and Rotated BRIEF，ORB）等。其中，由Lowe 提出的SIFT 算法[2]匹配的特征点数目较多但是计算耗时较长。SURF 算法是在SIFT 算法上引入了积分图像以及盒函数，从而获得了比SIFT 算法快3 倍的计算速度[3]。ORB算法是将加速段测试特征（Features from Accelerated Segment Test，FAST）算法和二值鲁棒独立基本特征（Binary Robust Independent Elementary Features，BRIEF）算法结合，计算速度快但尺度不变性较差[4]。在图像融合方面，航拍图像最常用的融合算法是加权线性融合算法。加权线性融合算法在处理单方向渐入渐出融合时效果较好，但是对于不同视角下拍摄出的航拍图像，图像变换后重叠区域通常会变得更加不规则，应用加权线性融合会导致较为明显的重影和拼接痕迹。

本文提出一种基于距离矩阵融合的无人机拼接算法。在特征检测阶段，本文采用SURF 算法来检测图像中的特征点，以期较快地获得准确的特征点和特征描述子。在特征点匹配阶段，计算描述子之间的欧氏距离并用最邻近规则分类（K-Nearest-Neighbors，KNN）算法对特征点之间进行匹配，对匹配后的特征点用随机抽样一致（Random Sample Consensus，RANSAC）算法剔除误匹配。在图像融合中采用距离矩阵算法，从而明显提高了图像在不同方向上融合时的效果，解决了多张航拍图像拼接时重影较大、拼接痕迹明显的问题。

1 图像匹配

1.1 SURF 算法提取特征点

1.1.1 构造尺度空间

通过不同大小的二维高斯模板对原图像进行卷积来构造出在不同尺度空间下的图像。二维高斯函数的表达式为：

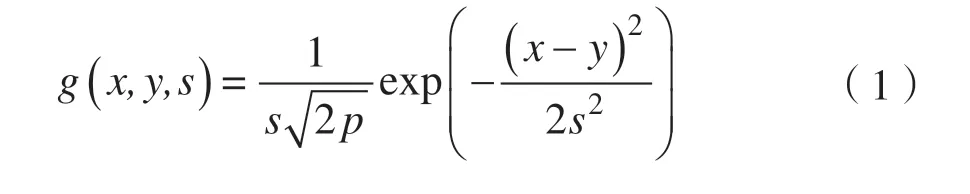
1.1.2 构造黑森矩阵

得到尺度空间后再用对每一个尺度空间下的图像用Hessian 矩阵卷积。

SURF 算法中采用了盒式滤波器模板近似代替高斯二阶滤波模板进行卷积计算，并将盒式滤波器用于积分图像上，从而显著降低了计算量。

通过二阶高斯函数滤波的黑森矩阵行列式的计算为：

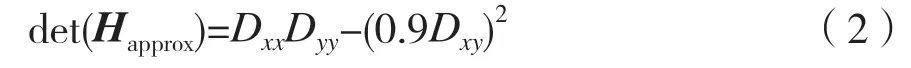
式中：Dxx、Dyy、Dxy分布代表xx、yy、xy方向上的盒式滤波器模板计算结果。

1.1.3 特征点提取

在相邻尺度空间上将像素点与其领域的26 个点进行对比，当该点Hessian 矩阵的判别式取得局部极大值时，判定当前点是比周围邻域内其他点更亮或更暗的点，由此来定位关键点的位置。

1.1.4 主方向的定义

本文选用Harr 小波特征来表示特征点在不同方向的灰度变化剧烈程度，统计特征点圆形邻域内的Harr 小波特征，并通过计算每60°扇形内的Harr 小波特征值的总和来确定特征点的主要方向。

1.1.5 建立特征点描述子

以特征点为中心，以主方向为基准，选择一个边长为20 像素点的正方形区域，通过Harr 小波特征来描述该区域的灰度变化。从而以Harr 小波特征和主方向为基础，建立特征点描述子。

特征点描述子的元素描述了特征点附近区域的灰度变化信息。由于是以主方向为基准进行的构建，特征点描述子能有效消除图像旋转的影响，使特征点的匹配更高效。

1.2 特征点匹配与筛选

本文采用KNN算法来进行特征描述子的匹配，并通过计算欧式距离来衡量两个描述子之间的相似程度。假设u、v分别为小图和大图的特征点描述子所构成的64 维向量，uik和vjk是第i、j个特征点描述子的第k个元素，则特征描述子之间的相似程度可以表示为两个64 维向量之间的欧氏距离：

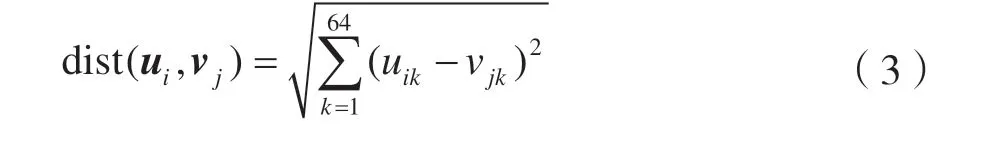
KNN 算法计算出与待匹配点距离最近的两个特征点，分别叫做最近邻点和次近邻点。通过对比两点距离的比值和设定的阈值来判断是否将待匹配点和最近邻点视作一个匹配对。

通过KNN 算法[5]得到的预匹配点对往往还存在较高的误匹配率和重复匹配点对，因此为了得到更加精确的匹配点对，减少图像拼接时的误差，还需要进一步进行精确匹配。

本文采用RANSAC 算法[6]对KNN 算法得到的匹配点对进行筛选。RANSAC 算法对包含离群值的一组数据进行数学模型的估算与构建，并通过不断迭代计算出包含最多内点的最佳模型估计。

2 基于欧氏距离映射的图像融合

目前图像融合大多采用线性加权融合或缝合线拼接算法。但线性融合算法的拼接痕迹较为明显，且不适用于任意方向拼接，而缝合线算法则存在拼接线两侧曝光差异较大且计算量较大等问题。为解决图像任意方位融合的问题，本文引入了欧式距离变换算法。

与线性融合算法一致的是，欧氏距离算法融合图像的原理仍是两个待融合的图片重叠区域上的每个像素点先乘上对应的权值，再将乘上权值后的图像相叠加从而得到融合图像。同时，在施加融合权值时，为了尽可能地减轻重影，并且消除图像重叠区域边缘在融合后图像中的明显拼接痕迹，分配给原图像边缘像素点的权重应该尽可能低，而给原图像中心处分配较高的权重。欧氏距离变换就可以产生此类型的权重矩阵。

图像的欧氏距离变换即为将图像二值化后，计算其中每个像素值为1 的点到其最近的像素值为0的点的欧氏距离，并将得到的结果根据位置依次映射到一个跟原图像大小相同的矩阵上，从而得到距离变换矩阵。如图1 所示：左侧为二值图像，（*）表示特征像素点，即图片所在位置，（-）表示非特征像素点，即画布背景；右侧为变换后的图像，即为一个距离矩阵。

图1 欧式距离变换

欧氏距离变换有多种算法[7-9]，本文则采用真欧几里得距离变换的快速算法[8]。将上述方法用在两幅图上，可以得到两张图片在拼接背景下的欧式距离变换矩阵，分别记为w1和w2。两个矩阵在归一化后相当于如图2 所示的灰度图像。

图2 基准图像和变换图像的距离变换矩阵

之后取两个张图片重合区域下的归一化距离矩阵值进行加权分配，即：

由于重合时一个图片的边缘往往在另一个图片的中心，因此可以实现边缘权重严格为1 或0，并且减轻部分鬼影。

通过以上步骤，即可得到满足如下条件的掩码：重叠部分与原图片相接的边处权值严格为1；与另一张图片相接处严格为0；中间平滑过渡（即保证融合后的图像在重叠部分各个边处与该边相邻的图片一致）。两幅图重合区域的掩码可视化后如图3所示。

图3 重叠区域权值灰度

算法过程总结如下：

（1）通过得到的特征点匹配对计算变换图像经透视变换后的图像大小以及两张图像拼接后所需的最小背景板大小；

（2）将基准图像和经过透视变换后的变换图像分别加到像素值全为0 的背景板上；

（3）将放置了图像的背景板进行欧氏距离变换，得到其对应的欧式距离矩阵；

（4）将欧式距离矩阵在重叠区域进行加权处理，分别得到基准图像和变换图像在重叠区域的权值。

3 实 验

3.1 实验数据集

为了说明本文方法的有效性，搜集了一些真实的无人机数据集，包括池塘和机场等实际场景的航拍图片等进行拼接实验。

机场数据集是在巴黎布尔热机场通过两架距地面120 m 同步飞行的无人机采集得到的。共包含557 张俯视角度照片，每张大小都为4 608×3 456像素。数据集包含机场的楼房、草坪和路面等多种环境，但视差相对较小。

池塘数据集是在池塘附近通过单一无人机拍摄采集得到的，共包含50 张分辨率4 000×3 000 的JPG 图像。其完整记录了无人机起飞到降落的过程，因此视差较大，本文采用其飞行平稳过程中的几张进行拼接。

3.2 实验配置

实验所用硬件配置为：CPU Intel Core i7-8750H（2.20 GHz），内存32 GB。采用MATLAB R2020b作为仿真软件。

3.3 实验结果分析

分别选取上述的两个数据集中的两组图片进行拼接，以此来对比本文方法与常用的线性加权融合方法，结果如图4、图5 所示。

图4 机场数据集融合效果对比

图5 池塘数据集融合效果对比

如图4、图5 所示，本文的算法对各个方向的拼接都可以实现平滑过渡。拼接后除了多个原始图像的重合区域有轻微重影以外，其他部分并没有明显的重影出现。

接下来本文将对两个数据集中的多张图像进行拼接，以此来验证本文方法对于多张无人机图像拼接的有效性，结果如图6、图7 所示。

图6 机场数据集22 张图像拼接结果

图7 池塘数据集11 张图像拼接结果

从图6 和图7 中可以看出，拼接完成的图像中鬼影较少，且拼接痕迹基本被消除。

4 结语

本文提出了一种基于欧式距离变换的无人机图像拼接方法。在特征匹配方面，采用SURF 算法提取特征点，并运用KNN 和RANSAC 算法完成匹配和误匹配的去除。在图像融合方面，采用欧氏距离变换产生权重矩阵，对两张图像加权融合。实验结果显示，本文的方法可以对不同类型、不同方向的拼接产生平滑过渡的效果，并且能够很好地解决线性融合中拼接痕迹和鬼影的问题。在实际的无人机图像集拼接中，可以较好地完成对多张图片的拼接，而不产生或较少地产生重影、错位及拼接痕迹等缺陷。