基于矩阵分解填充的无监督特征选择方法*
2021-08-30范林歌武欣嵘曾维军
范林歌,武欣嵘,童 玮,曾维军
(陆军工程大学,江苏 南京 210007)
0 引言
随着科技的飞速发展,产生了大量数据,而且用于数据挖掘的数据维数越来越大,但高维数据不可避免地含有冗余信息,这不利于后续的数据分析与挖掘。特征选择和特征提取是处理这些高维数据的有力工具。它们的主要区别是特征选择保留原有特征,而特征提取产生新的特征。但是特征选择更具有可解释性,所以本文将重点放在特征选择技术上。
特征选择的目标是从原始特征中选择一个子集,这些子集对后续的任务具有信息性和价值。此外,所选特征还可以加快数据处理速度,提高模型的泛化能力。根据是否使用标签信息,特征选择方法可以分为监督特征选择[1]、半监督特征选择[2-3]和无监督特征选择[4](Unsupervised Feature Selection,UFS)3 种不同类型。有监督特征选择通过评估特征与类标签的相关性来确定特征相关性,半监督特征选择同时使用有标签(数量少)和无标签(数量多)数据,而UFS 利用数据方差和可分离性来评估没有任何类标签的特征的相关性。在许多现实应用程序中,数据标签难以获得,重建模型的代价也很高。因此,无监督和半监督的特征选择方法更为实用。本文主要研究UFS。
传统的UFS 方法,比如主成分分析分数法(Principal Components Analysis,PCAScore)[5]和拉普拉斯分数法(Laplacian Score,LapScore)[6],根据为每个特征计算的分数选择排名最高的特征。Liu 等人[7]提出了一种新的称为多群集特征选择(Multi-Cluster Feature Selection,MCFS)的方法,用于UFS。MCFS 考虑了不同特征之间可能的相关性,并使用了数据的光谱分析(流形学习)和正则化模型进行子集选择。Liu 等人[8]提出了一种新的嵌入式模型的光谱特征选择算法,联合评估了一组特征的效果,可以有效地消除冗余特征。
然而,在实际应用中,一些样本中含有未观察到的信息。一方面,一个工业数据集甚至可能会遗漏整个信息的90%[9-10]。另一方面,大多数UFS 技术的设计针对完整的数据集。该数据集的整个信息都是可观察的,因此这些技术不能直接应用于不完整的数据集。最近,人们提出了一些解决方案来处理未观察到的数据,对不完整数据集进行特征选择。
文献[11]等设计两阶段策略对不完整数据集进行特征选择,即使用估算方法猜测未观测信息的值,然后使用已有的技术对估算数据集进行特征选择。例如,基于条件熵[12]的特征选择方法,使用基于熵的不确定性度量来处理未观察到的信息进行特征选择。然而,传统的特征选择算法只是简单地使用统计特征来对特征进行排序,没有对变换矩阵进行有效地学习。在不填充直接进行UFS 方面,文献[13]考虑到样本的重要性,提出了一种新的在不完全数据集上进行UFS 的方法。该方法利用指标矩阵对未观测信息进行处理,过滤掉特征选择过程中的未观测信息,并利用半二次最小化技术自动地给离群点分配较小甚至为零的权值,给重要样本分配较大的权值,从而减少离群点的影响。
本文基于先填充后特征选择的流程对不完整数据集进行UFS。传统的填充方法只单一地参考某一列或某些样本对缺失值进行填充,不准确的填充会进一步影响后续的数据分析。针对以往方法填充不够准确的问题,本文提出使用矩阵分解的方法对不完整数据集进行估算,利用矩阵乘法的固有特性对数据集中的可观测信息进行充分利用,并结合基于ℓ2,1范数的无监督最大间隔特征选择方法,将特征选择和K-means 聚类结合成一个连贯的框架来自适应地选择最具鉴别性的子空间,以 ℓ2,1范数作为稀疏约束,迫使投影矩阵W行稀疏,进而更有效地选择最相关的特征,通过对最优子空间和聚类的交替学习,得到特征选择结果。最后,本文分别在合成数据集和真实数据集上进行方法验证,实验结果表明,本文所提方法和其他经典算法相比获得了较高的分类准确率。
1 基于矩阵分解的缺失值填充方法
考虑不完整数据集X=[x1,x2,…,xn]∈RM×N,其中n=1,…,N,N为样本数,M为特征数,xn为第n个给定样本,xn(j)表示第n个样本的第j个特征,j=1,…,M。
首先对数据进行标准化预处理操作。一般来说,数据标准化方法包括最小最大标准化和Z-score 标准化等方法。为了便于分析,本文采用最小最大标准化将数据值转化为[0,1]区间内的值,计算公式为:
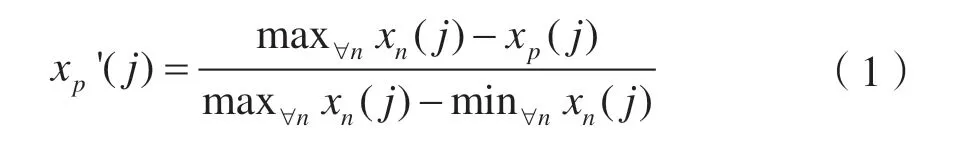
式中,j=1,…,M。
由于直接使用不完整数据集中所有样本来预估缺失值计算量较大,本文先对不完整数据集进行K近邻(K-Nearest Neighbor,KNN)预填充,再使用经典的K-means 聚类方法将原始无标签数据集进行聚类,给予每个样本一个伪标签。K-means 聚类是一种基于距离的无监督聚类算法,在给定聚类个数和初始类簇中心点的情况下,把每个点分到离其最近的类簇中心点所代表的类簇中。假设第i簇数据集为X i,为第n个样本经过第一次K-means 聚类后对应的伪标签,=1,2,…,T,其中T为聚类个数,每一簇数据集样本选择为:
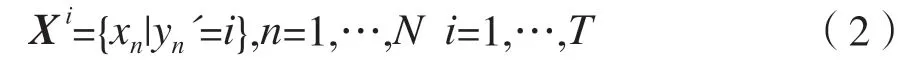
式中:第i个簇中包含Ti个样本。
X i具体表示为:
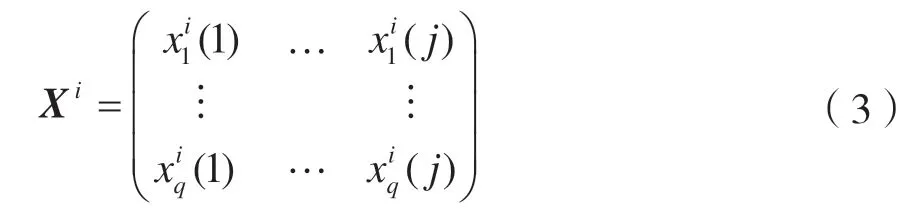
本文基于假设具有相同伪标签的两个样本相似度比具有不同伪标签的两个样本高。通过初始分簇达到在减少计算量的基础上不降低填充准确性的目的,之后分别对每簇中的缺失值进行估计。
在计算过程中利用置信度矩阵对未观察到的信息进行过滤,从而达到利用完整和不完整样本中所有有效信息的目的。对于给定的不完整数据集X,定义置信度矩阵I,其中In(j)反映第n个样本的第j个特征的缺失情况,元素取值为:

则第i簇数据集X i对应的指示矩阵为I i。
本文期望将X i分解为矩阵U和V的乘积,其中U∈RL×K,V∈RM×K。由于现实应用中大多数矩阵不能做出这样完美的分解,因此本文寻找第i簇数据集X i的一个近似矩阵。可以分解为矩阵U和V的乘积,通过求解来代替原始数据簇中缺失的值,定义为:
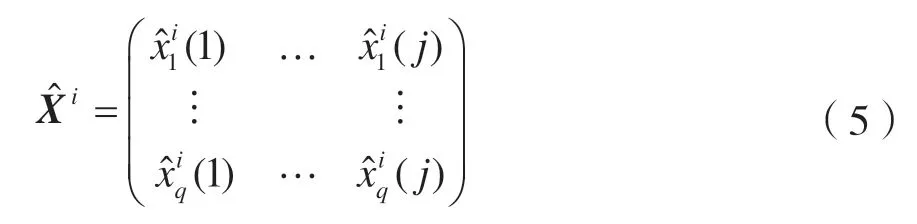
近似矩阵可分解为U和V矩阵,使得:
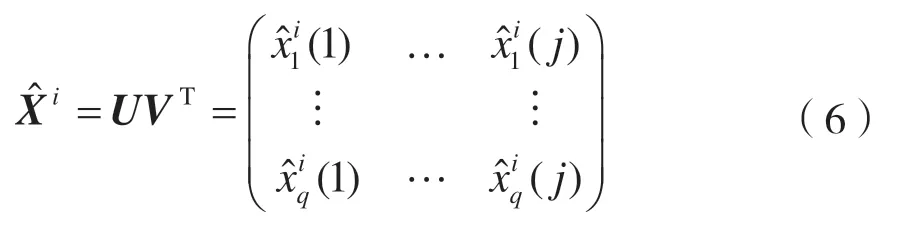
式中:矩阵U和V分别表示数据集样本和特征的隐藏特征。比如在一个用户对多部电影评分的数据集中,xq(j)表示第q个用户对第j部电影的评分,此时U和V分别描述用户的特征(比如年龄段等)和电影的特征(比如演员、题材、主题等)。
均方根误差(Root Mean Squared Error,RMSE)可以用来衡量真实值与预估值之前的差距,本文通过计算目标矩阵X i与近似矩阵的均方根误差RMSE 来评估模型性能,X i与的均方根误差RMSE 定义为:
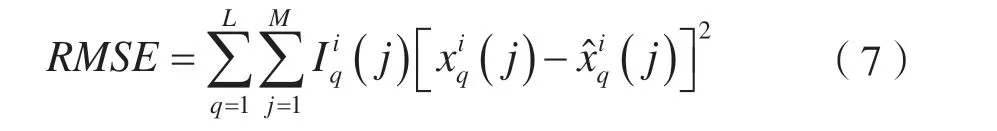
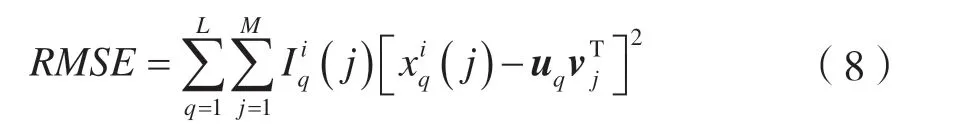
RMSE 值越小则表示填补效果越好。本文通过求解一组U和V使相似矩阵与目标矩阵X i的RMSE 最小,至此该问题可以优化为:

这里采用梯度下降的方式迭代计算U和V,首先固定V,对U求导,如:
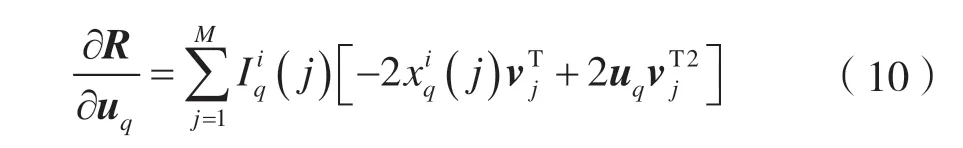
uq的更新公式为:
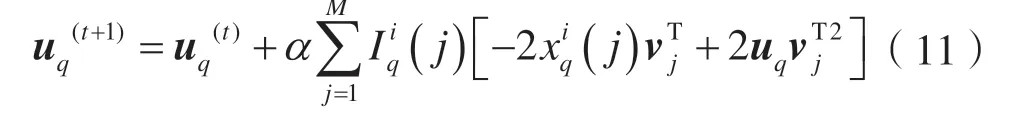
式中:α为更新速率,表示迭代的步长。
其次,固定U,对V求导,得:
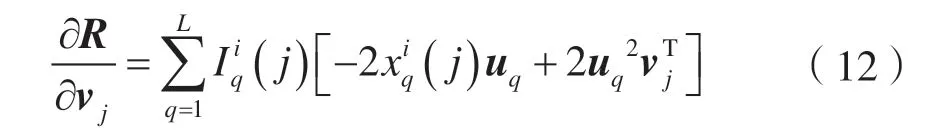
vj的更新公式为:
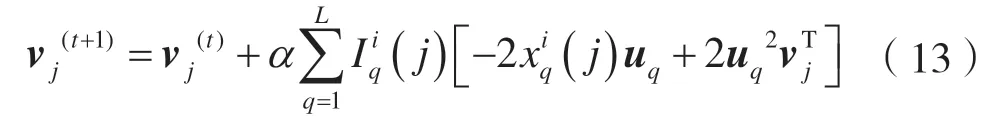
重复式(11)与式(13),迭代优化U和V,直到RMSE<ζ为止,ζ为自定义误差。
遍历所有i,对每一簇数据进行如上操作,直到Io=0 即数据集无缺失为止。至此,求出X i的近似矩阵,用中对应位置的数据填充X i中的缺失值。Io定义为:之后对填充好的数据集X进行UFS。

2 基于 ℓ2,1 范数的无监督最大间隔特征选择
2.1 最大间隔准则
最大间隔准则(Maximum Margin Criterion,MMC)是基于特征空间的类间散度与类内散度的差的最大化,其目的是寻求一组最佳鉴别矢量为投影轴进行投影变换,使得特征空间样本的类间散度最大和类内散度最小。因此,特征选择标准的定义为:
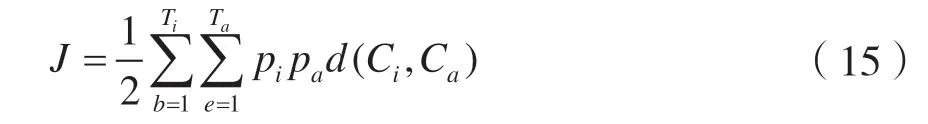
式中:Ti和Ta分别表示第i类和第a类的数量;pi和pa分别为第i类和第a类的先验概率;Ci和Ca分别表示第i类和第a类,类间隔定义为:
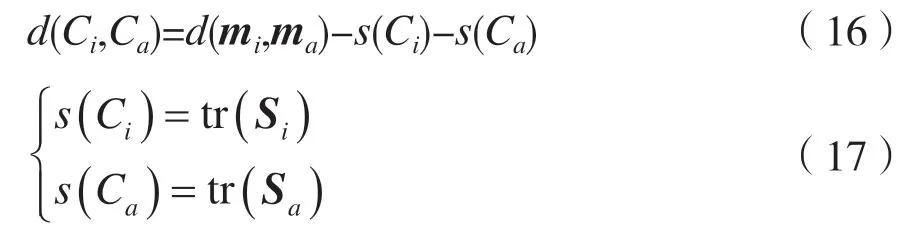
式中:mi和ma分别为类Ci和类Ca的均值向量;而Si和Sa分别为类Ci和类Ca的协方差矩阵。通过简单的数学运算,可以得到公式:

式中:Sb为类间散射矩阵,Sw为类内散射矩阵,定义为:
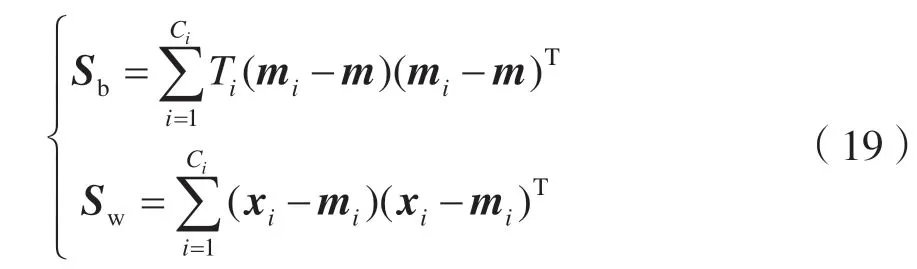
式中:Ti为类Ci的数量;m为所有数据的平均向量。至此,MMC 可以表述为:
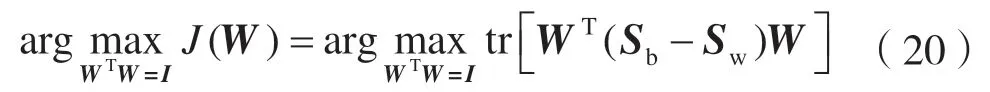
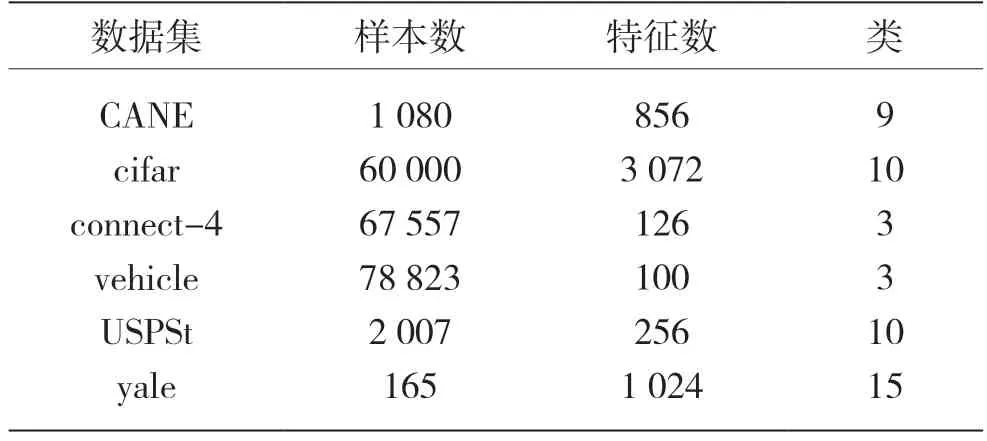
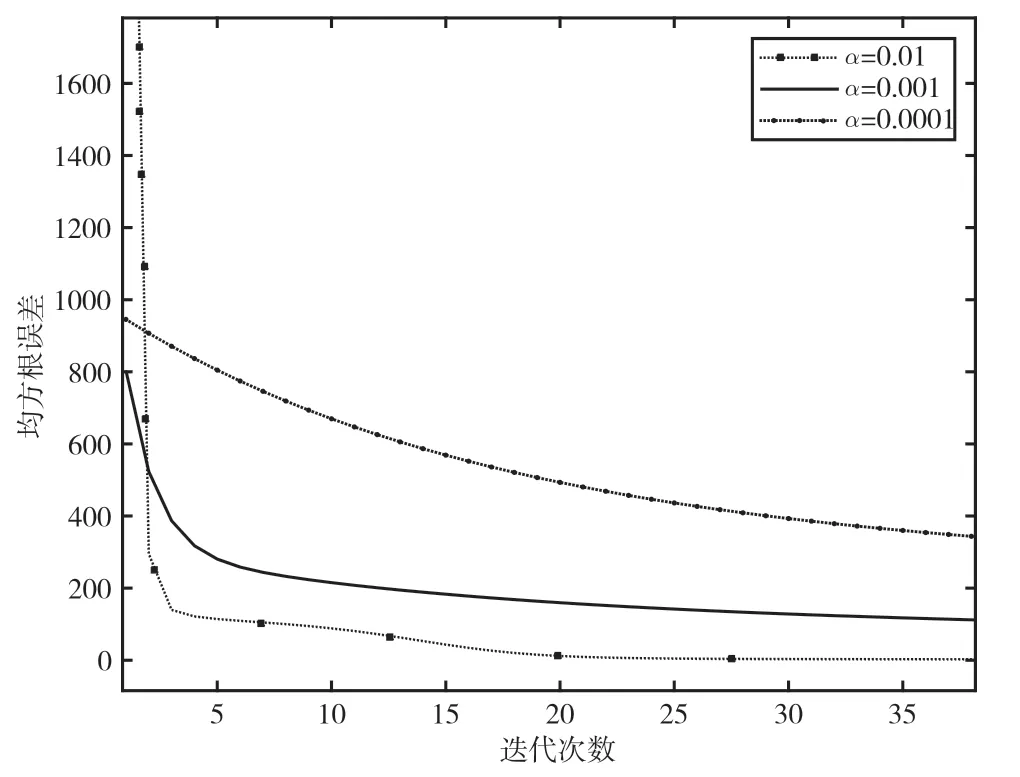
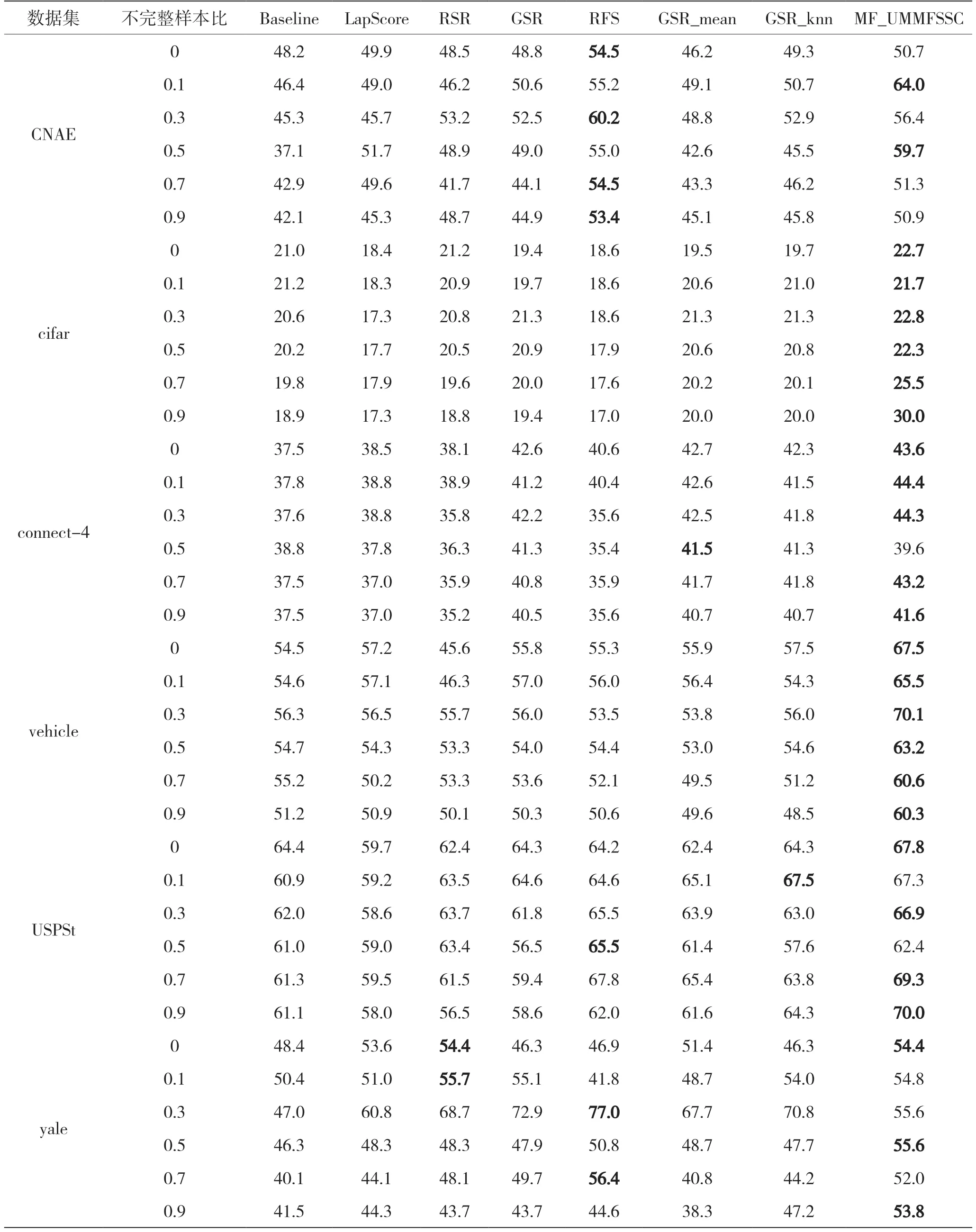
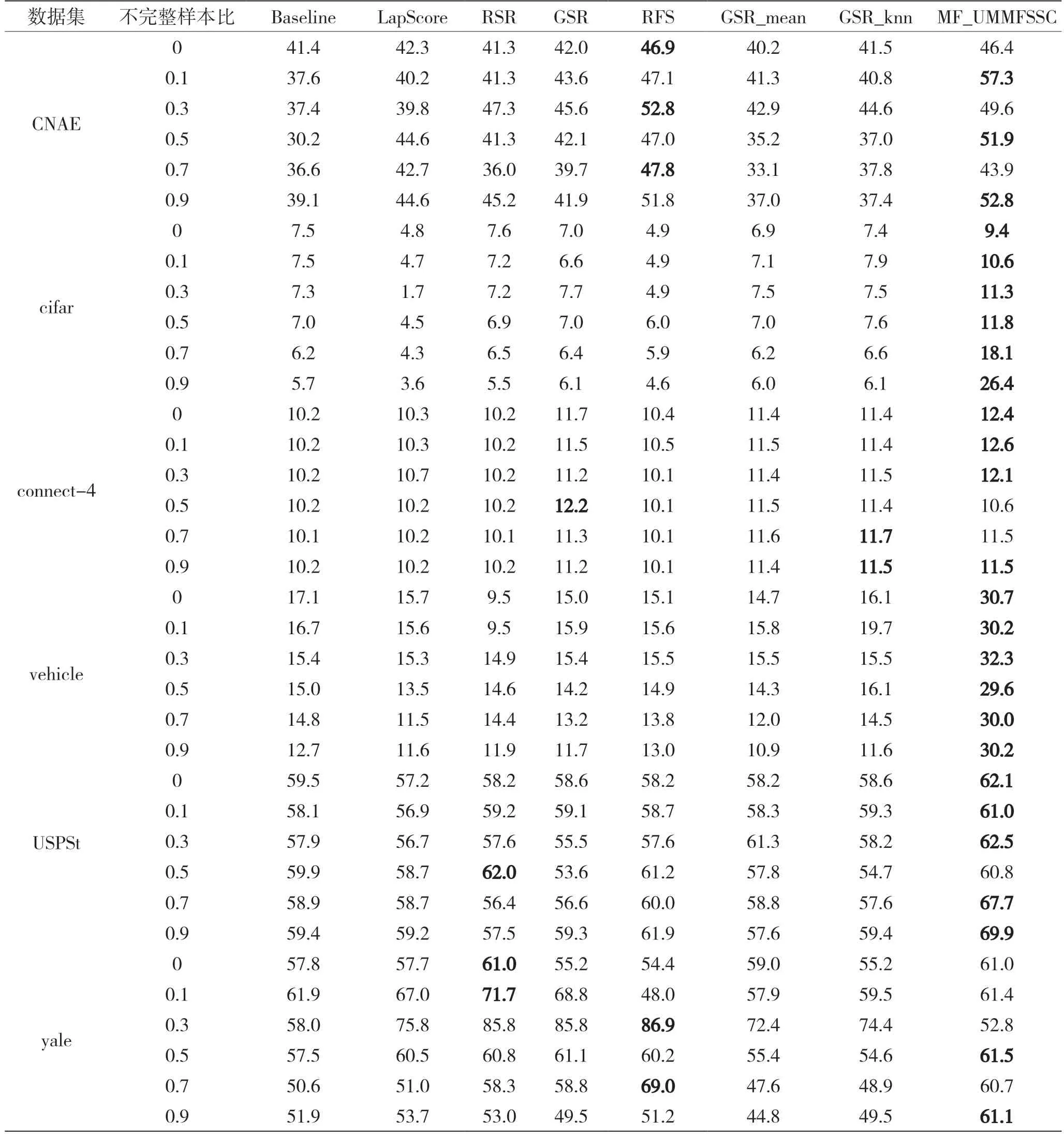
式中:W∈RM×d为投影矩阵;d W由Sb-Sw的前d个最大特征值对应的特征向量组成。这里不需要计算Sw的逆,可以避免小样本量的问题。 本文数据集为X=[x1,x2,…,xn]∈RM×N,M个特征,N个样本,选择d个特征来代表原始数据,构造对角矩阵D∈RM×M,其取值如: 式中:w j表示矩阵W的第j行,聚类簇的数目初始为C,定义指示矩阵F∈RN×C,则有: 然后通过稀疏约束(Unsupervised Maximum Margin Feature Selection via Sparse Constraints,UMMFSSC)表示无监督最大间隔的特征选择: 式中,α为正则化项参数,这里可以很容易地验证下列两个方程: 式中,A为单位阵。可近一步化为: 由式(27)可知,需要优化的变量分别为W、D、F。同时计算它们比较困难,在这里对它们进行交替优化。 首先,固定W,计算F。优化问题可以转化为: 本文使用谱分解技术来解决这个问题。矩阵XTWWTX的前c个最大特征值对应的特征向量即为形成的最优F。 其次,固定F,计算W和D。此时仍有两个变量需要优化,所以这里使用嵌套优化技术。首先固定W,此时可以根据式(27)更新D,其次固定D,此时优化问题变为: 这里仍然可以使用谱分解技术来解决这个问题。最优的W是由矩阵X(A-2FFT)XT+D的前d个最小特征值所对应的特征向量形成的。重复迭代过程直到算法收敛。至此,可以使用计算出的W来进行特征选择,稀疏约束迫使W的许多行为零,按降序对每个特征进行排序,并选择排名最高的特征。 至此,将基于矩阵分解的缺失值填充方法与基于 ℓ2,1范数的无监督最大间隔特征选择方法结合起来,形成基于矩阵分解的不完整数据集UFS 算法(Matrix Factorization_ Unsupervised Maximum Margin Feature Selection via Sparse Constraints,MF_UMMFSSC)具体描述如下所示。 输入:不完整数据集X∈RN×M,特征选择数目d,正则化参数α; 输出:W∈RM×d; 初始化U,V和D; 步骤1:根据式(1)将原始数据集进行标准化处理; 步骤2:根据式(2)、式(3)将原始数据集分簇,读取第i簇数据, 重复; 步骤3:根据式(10)更新U; 步骤4:根据式(12)更新V; 直到RMSE<ξ 步骤5:遍历所有i,填充所有缺失值 重复; 步骤6:固定W,由式(28)求得此时的最优F; 步骤7:固定F; 步骤8:固定W,计算对角阵D,其元素取值为djj=1/(2||w j||2); 步骤9:固定D,计算W,由式(29)求得此时的最优W; 直到收敛; 步骤10:使用计算得到的W进行特征选择,根据W降序排列特征,选择排名靠前的特征。 为了评估所提算法的有效性,分别在6 个不完整数据集上进行实验,与4 种已有的特征选择方法进行比较,评估它们在高维数据上的聚类性能。 本节使用了两个评估指标:分类精度(Accuracy,ACC)和归一化互信息(Normalized Mutual Informaion,NMI)。ACC 表示样本分类正确的百分比,即: 式中,N为样本总数,Nc为正确被分类的样本个数。 NMI 则揭示预测情况和实际情况之间的相关性,定义为: 式中:I(X,Y)表示预测标签与真实标签的互信息;H(·)为熵运算。 本小节分别从LIBSVM 数据网站、UCI website等知名数据集网站下载6 个真实数据集:CNAE、cifar、connect-4、vehicle、USPSt、yale。其中:CNAE是一个描述巴西公司经济活动业务的数据集;cifar是一个用于识别普适物体的小型数据集,一共有60 000 张32×32 像素的彩色图片;connect-4 数据集包含connect-4 游戏中所有合法的8 层位置,USPSt 是美国邮政手写数字数据集,用于模式识别、机器学习算法的验证;yale 为耶鲁大学的人脸数据集数据集。详细信息如表1 所示。 表1 数据集介绍 为了观察缺失率对算法的影响,将观察到的信息随机标记为未观察到的信息,不完全样本率从0%~90%,以10%为间隔递增,不完整样本率为不完整样本占总样本数的比率。在此仅考虑缺失机制为完全随机缺失的情况。对经过填充的完整数据集,通过特征选择方法去除50%的特征来分析算法的结果。 本文使用已有的4 种特征选择方法来进行比较,将用来比较的方法简要叙述如下。 (1)拉普拉斯分数法(LaPscore):基于一个过滤模型,依据所有特征的拉普拉斯分数来评估每个特征的重要性。 (2)基于正则化的无监督特征选择(Regularized Self-Representation,RSR):使用特征级别的自表示来重构每个特征,然后使用 ℓ2,1范数正则化进行特征选择。 (3)通用稀疏正则化框架(General Framework for Sparsity Regularized,GSR):是一种通用的稀疏嵌入模型,可以同时进行特征选择和通过参数调整来减少异常值。 (4)鲁棒特征选择(Robust Feature Selection,RFS):是典型的特征选择嵌入模型,验证了其减小异常值影响的有效性。 在本文实验中,将每个不完整数据集分为两个子集,即包含所有不完整样本的不完整集(Incomplete Set,IS)和包含所有观察样本的观察集(Observed Set,OS)。具体流程如下: (1)将基于OS 原始特征进行K-means 聚类的方法标注为Baseline。 (2)采用上述的过滤模型,即LaPscore,和3种嵌入式特征选择方法,即RSR、GSR 和RFS,对OS 进行特征选择,然后对选择的特征在OS 上进行K-means 聚类。 (3)利用OS 中的信息通过填充方法,即均值填充(Mean-Value Imputation Method)和KNN 填充(KNN Imputation Method)来填充IS中未观察到的值。 (4)对OS 和IS 的结合(即OS ∪IS)进行特征选择,即GSR,得到GSR_mean 和GSR_knn,然后对所选特性在OS 上进行K-means 聚类。 (5)使用本文提出的算法即MF_UMMFSSC 在IS 上填充,然后在OS ∪IS 上进行特征选择然后利用所选特征在OS 上进行K-means 聚类。 本实验环境为MATLAB2019a,如前文所述,K为矩阵U和V的维度,当其取不同值时均方根误差RMSE 的收敛速度如图1 所示。这里分别取K=1、5、10、15、20。可以看到,K=1 和5 时收敛速度较慢并且无法收敛到0;当K=10、15、20 时均方根误差收敛较快,并且可以收敛到0。可见,K的取值不光影响均方根误差收敛速度,还会影响最终收敛结果。为了不增加计算量并且防止过拟合,本文所有实验均设置K值取10。 图1 不同K 值均方根误差随迭代次数变化 不止K的取值,学习速率α的取值不同也会影响均方根误差的收敛速度,如图2 所示。α分别取0.1、0.01、0.001、0.000 1,由图2 可见,α取0.01时收敛速度最快,α取0.000 1 时收敛速度最慢。由此可知,步长越小,损失函数到达底部的时间越长;步长越大,损失函数收敛越快。但步长并不能无限大,经过实验发现当α取0.1 时,目标函数不会收敛,所以在该合成数据集上α取0.01。经过在不同数据集上的实验也发现,同一个步长并不适用于所有数据集,要多次实验发现最适合本数据集的步长,本文中所有数据集步长设置均经过多次实验,并设其为最恰当的数值。 图2 不同α 值均方根误差随迭代次数变化 本文采用10 倍交叉验证方案,将每种方法在每个数据集上重复10 次并展示这10 次的平均结果,每一次都是10 个K-means 聚类结果的平均值。这里将K-means 聚类中的簇数设为数据集的真实类数。 表2 和表3 为本文提出的算法MF_UMMFSSC在不同不完整样本比时在不同数据集上的聚类结果,这里展示ACC 和NMI 指标,每一行的最大值加粗表示。 由表2 和表3 可知:在大部分数据集上本文提出的算法取得了较好的ACC 和NMI,MF_UMMFSSC 在大数据集上的改进大于在相应小数据集上的改进。整体来说,随着不完全样本比的增加,所有方法的聚类性能都有所下降。在vehicle 数据集上,不完整样本比为0.1 和0.9 时,聚类准确率下降了5.2%。在CNAE 数据集上,RFS 的效果较好,本文提出的算法效果并不是最优,但是和其他的先填充再进行特征选择的方法相比,MF_UMMFSSC仍取得了不错的效果。由此可见,同样的方法在不同数据集上效果是不同的。在cifar 数据集上,准确率也有一定的提升,尤其是在不完整样本率90%时,该方法准确率提高了10%;在connect-4 数据集上,本文提出的算法也基本达到了最高的准确率;在不完整样本率为50%时,GSR_mean 方法的准确率最高;在vehicle 数据集上,MF_UMMFSSC 效果最好,和之前的算法相比,在所有的不完整样本率条件下,准确率都提高了10%左右,随之NMI也有大幅提升;在USPSt 数据集上,本文提出的算法也取得了较好的结果;在yale 数据集上,RSR 方法在不完整样本比较低时效果较好,本文提出的方法在该数据集上效果不是最好,但也比大部分方法好。综上所述,MF_UMMFSSC 在大部分的数据集上取得了较好的聚类准确率,提高了填充效果。 表2 各个数据集在不同不完整样本比下进行聚类的ACC 结果 表3 各个数据集在不同不完整样本比下进行聚类的NMI 结果 现实应用中,高维数据中存有大量包含未观测信息的样本,获取样本标签也较为困难而且消耗大量成本,此时UFS 方法的研究更具有现实意义。然而大多现有的方法不能直接应用于不完整数据集,现有填充方法对不完整数据集的信息利用不够完全。针对这些特点,本文提出MF_UMMFSSC,该方法利用所有已知信息对不完整数据集进行填充,之后利用基于 ℓ2,1范数的无监督最大间隔特征选择方法进行特征选择,在6 个数据集上的实验结果表明,本文所提出的算法提高了聚类精度和填补效果。
2.2 无监督最大间隔特征选择
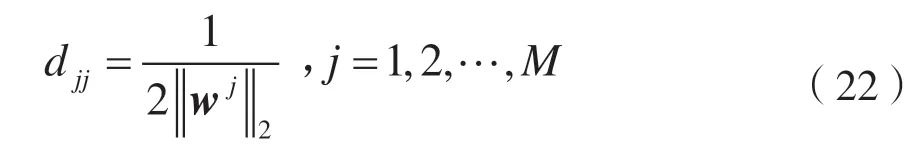

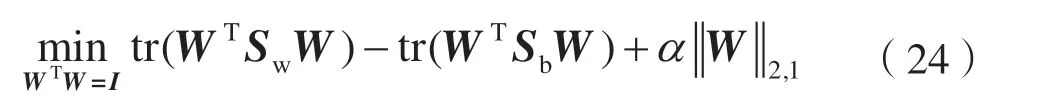

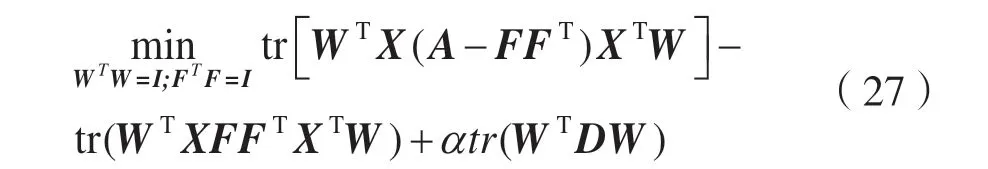
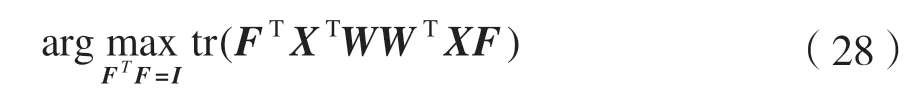
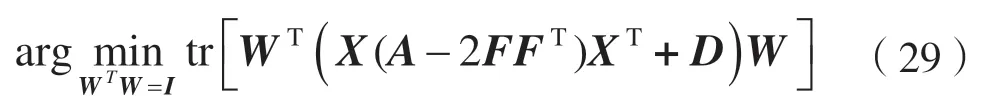
3 实验及结果分析
3.1 评估指标及数据集


3.2 比较算法
3.3 实验设置

3.4 实验结果
4 结语
