郊域轨道交通对土地利用演变的影响分析
2021-08-28李俊芳姚敏峰胡华
李俊芳,姚敏峰,胡华
(1.上海工程技术大学,城市轨道交通学院,上海201620;2.华侨大学建筑学院,福建厦门362021)
0 引言
郊区新型城镇化是我国新型城镇化主要发展方向之一,在国家公布的第三批新型城镇化综合试点地区中,北京市顺义区等均属郊区。近期上海全力推进将五大郊区新城建设成为长三角地区具有辐射带动作用的综合性节点城市的议题揭示了上海郊区新型城镇化的内涵与重要性。大运量轨道交通被公认为是新型城镇化发展的核心动力之一[1]。大城市的郊区与市区间多建设有轨道交通以促进郊区发展,但郊区城镇间暂无线路(连接郊区城镇的线路即郊域轨道交通线路,简称郊域线)。据笔者统计上海轨道交通起始站均为郊区车站的全日客流量占全网客流量的34.7%。国外为了促进郊区发展,大城市多建有郊域线[2]。国内郊区间出行需求的压力与国外的实践充分说明了郊域线建设的必要性与可行性,同时作为我国新基建的主要领域,建设郊域线不仅在技术层面能切实有效解决郊区间出行问题,同时在战略层面,借助郊域线深入推进郊区新型城镇化,能够将国家当前的两大战略目标较好地融合在一起,符合国家战略需求,具有深远意义。上海郊域线嘉闵线已于2021年开工,可以预见郊域线将愈受关注。
城市轨道交通是引导城市土地开发建设的重要媒介,能够带动土地整合,优化城市结构。已有诸多学者针对城市轨道交通对土地发展的影响展开了研究[3-4],轨交线引起的土地利用演变(Land Use Change,LUC)也是学术界研究的热点之一[5-6]。郊域线LUC规律是科学开发郊域线周边土地的依据,是郊域线与郊区新型城镇化土地利用协调发展的基础,目前国内郊域线尚属新兴事物,此阶段对郊域线LUC规律展开研究是有必要且有意义的。目前既有研究多集中于市郊线的LUC 规律,鲜有涉及郊域线;主要是对LUC结果进行简单统计,鲜有涉及影响因素与LUC间关系,即LUC机制的研究。谭章智[3]研究了广州市地铁2 号线与8号线周边2000年,2006年,2010年与2015年土地利用状态(Land Use,LU),通过对比找出变化的地块后,得到站点周边低密度居住用地向商业用地、高密度居住用地等高效益LU 的转变,且具有阶段性与空间异质性规律,对城市中心区域的影响较小,对郊区的影响主要与可用的非建设用地面积相关。吴韬[4]对天津地铁1号线2006年与2017年LU进行对比后发现:城市核心区域站点设施相对完善,地块更新较少,沿线土地功能结构更趋于混合利用,商业用地明显增加,工业仓储用地则相应减少;居住用地比例变化不大,主要是低层住宅更新为高层住宅,开发强度更大。由于郊域线与市郊线服务区域与功能不同,前者主要连接与服务郊区新城镇,如嘉闵线主要连接嘉定、闵行各主要城镇;后者连接了拥有大量就业岗位及商业娱乐活动频繁的市区,可以预见两者的LUC规律会有差异,故本文对郊域线的LUC规律与机制展开研究。
元胞自动机(CA)是模拟LUC 常用的仿真工具[7]。CA的核心转化规则即LUC机制常通过构建模型获取,其中线性或Logistic 回归模型难以反映LUC 所涉及的非线性复杂特征[7-8]。马尔科夫链无法处理社会经济类的定量因素[9]。故具有较高模拟精度与效率的人工智能算法被引进,如人工神经网络(ANN),但其黑箱机制使其无法反映因素对LUC的影响[10]。贝叶斯网络(Bayesian Network,BN)也是人工智能的典型算法,其具有很强的表达时空复杂性的潜力,用概率表达因子间的关系,与LUC问题的特性(LU 间的转化概率)较为匹配[11]。故本文采用BN 对郊域线的LUC 机制进行建模。LUC 受多因素影响,为减弱其他因素影响,研究郊域线对LUC的影响时,设计参照区,将轨交线缓冲区(客流吸引范围内)与参照区(客流吸引范围外)LUC 差异进行对比,同时将市郊线与郊域线进行对比。最后以东京郊域轨道交通多摩线为案例,验证方法的可行性与适用性。
1 LUC模型
1.1 贝叶斯定理(Bayes)及BN
Bayes 与BN 均用于表达与分析不确定性和概率性问题。Bayes 表达两个变量间的概率,公式为。其数学解释为在变量B发生时,变量A发生的概率取决于既有数据中两者的先验概率及两者之间的概率关系。BN 是Bayes 的扩展,在目标变量有条件地依赖多种控制变量的情况下,从既有的知识或信息中做出推理,最终做出决策。BN 是一个有向无环图,常用表示,其中,I为图中的结点集合,E为有向连接线段的集合。结点代表随机变量,结点间的有向边代表结点间的互相关系(由父结点指向其子结点),用条件概率进行表达关系强度,没有父结点的用先验概率进行信息表达。图1为BN的简单例子,其中,X1,X2,X3,X4均为网络结点。

图1 简单的BNFig.1 Simple BN case
图中箭头从X1指向X3,X1称为X3的父结点,X3称为X1的子结点。BN适用于连续与分类变量,对于后者,每个结点附属有该结点对应变量在其父结点确定时的条件概率表(如果没有父结点如X1与X2,就是各自的先验概率)。所有概率表集合定义了模型的参数。
1.2 BN求解、推理与模式分析
通过网络结构与参数学习实现求解。结构可通过专家指定,但若结点间关系未知或部分已知,需通过学习观察数据得到,做法是在给定数据集中寻找变量间的条件独立性关系。基于网络结构和数据,采用最大似然估计法进行网络参数学习。
BN 因果推理是根据获得的自变量值,利用网络计算出该自变量值下因变量某具体值发生的概率。图1中当网络结构与参数学习完成后,在X1取值x1,X2取值x2时,X3的值为x3的概率可以直接从网络得出。由于BN的逆概率性,也可实施诊断与支持推理,其过程与因果推理类似。BN推理可用于预测。
为辨识某变量的关键影响变量,利用网络实施模式分析,计算目标变量某状态下各变量强度,公式为

式中:Xtest为待检验变量;Xtarget为目标变量;rtarget为目标变量的状态总数;k为目标变量除状态t外的状态值;为待检验变量强度计算函数。式(1)表示待检验变量在目标变量为状态t时与其在目标变量为其他状态时的距离,距离大说明目标变量为不同状态时待检验变量差异显著,说明目标变量对该检验变量的影响大。将同一目标变量的多个检验变量的强度进行对比可辨识目标变量影响最大的变量。如可辨识区域变量(缓冲区、参照区)影响最大的变量,则该变量有可能是受轨道交通影响最大的变量。
1.3 BN变量选取——轨道交通引起的LUC
目标结点变量是轨道交通建设后地块的类型,用“终态”变量表示,有田地,森林,荒地,建筑用地,交通用地,运动竞技用地,水域,草地8 个变量值。影响因素包含:①地块的初始利用类型,用“初始态”变量表示,同“终态”变量,有8 个变量值;②地块初始邻域地块状态,用邻域地块中各LU 的个数表示,含8 种地块类型变量,每个变量取值从0 到8(因为地块有8个邻域地块,属于某LU的个数不超过8),代表邻域地块中该类型地块的个数;③地块是否位于客流吸引范围内,用区域变量表示,有参照区、缓冲区2个变量值。
2 案例分析
2.1 案例介绍
鉴于国内缺乏完整的可获取的LU 数据,而东京都1987年,1991年,1997年,2006年,2014年的LU 数据全面且公开透明易获取,选择东京都作为研究城市。研究东京都郊域线的LUC 规律于上海、北京、广州等大城市具有很好的参考价值。以东京都郊域线——多摩线作为实证研究对象,并选取市郊线——7 号线作对比。多摩线1998年开通运营,7 号线1991年开通运营。东京都行政区划图、轨道交通网络图及多摩线与7 号线均见文献[4],东京都土地利用状态(以2006年为例)与两线车站位置如图2所示。鉴于轨道交通线路对LUC 的影响集中在一定范围,取线路2 km 缓冲区作为LUC研究范围[4]。
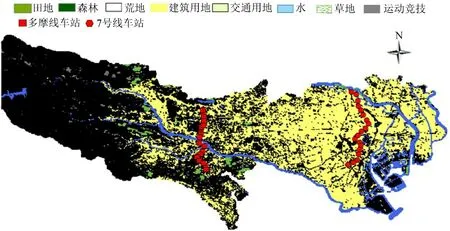
图2 东京都LU与线路车站位置Fig.2 LU in Tokyo and station sites of research lines
2.2 参照区选取
选择线路2 km缓冲区外同行政区的其他区域作为参照区,两线参照区范围见文献[4]。两线LUC 情况分别如图3 和图4所示。多摩线1998年开通,暂用1997年的土地利用数据。

图3 7号线LUC情景Fig.3 LUC of 7 Line by time
2.3 演变规律
采用Bayes Server[12]软件对网络进行结构构建与参数标定。两线LUC规律BN结构分别如图5和图6所示。图5中97终态与06终态两个终态变量,分别表示多摩线开通时与开通后LU;图6 中91 终态与97终态的解释同理。

图6 7号线LUC规律BN结构Fig.6 BN of land use change for 7 Line
(1)多摩线
图5 中,区域变量与97 终态和06 终态有直接关联,表明开通时和开通后LU与区域有关,说明多摩线建设与运营均对LUC 产生了影响;区域变量与初始邻域森林地块个数有直接关联,因为缓冲区即使在未建设多摩线之前,也属开发较多,森林占比较小的区域,与参照区森林占比有显著差异。初始态与97终态有直接关联,06终态与97终态、初始态均无关联,说明开通前LU 仅影响了开通时LU,运营期LU 不依赖初始态或前一时期状态,表明郊域线作为郊区LUC 的强驱动力,运营后引起LUC活跃程度较大。模式分析结果如表1所示。

表1 多摩线LUC规律BN模式分析Table 1 Pattern analysis for BN of Tamatoshi monorail line

图5 多摩线LUC规律BN结构Fig.5 BN of LUC for Tamatoshi monorail line
从表1 可以看出,区域变量取为缓冲区时,强度较大的变量依次是初始邻域森林地块个数、06终态,初始邻域建筑用地个数以及97 终态。表明缓冲区与参照区上述变量出现了显著差异,初始邻域森林地块个数、06终态,97终态变量与上文分析一致。初始邻域建筑地块个数的解释同初始邻域森林地块个数变量。
(2)7号线
区域变量与LU 终态没有直接关联,即缓冲区与参照区LUC 相似,没有显著区别,说明7 号线建设与运营对LUC没有产生显著影响,因为7号线大部分位于市区,市区LUC驱动力较多,即便是轨道交通线网也十分密集,7号线参照区内LUC会受到其他驱动力的影响而使得演变与7 号线缓冲区无差异;区域变量与初始邻域田地、森林地块个数有直接联系,说明未建设7 号线之前,其参照区与缓冲区的田地、森林用地个数有差异。初始态与91终态有直接关联,91 终态与97 终态有直接关联。市区LU 总是与前一时期LU 有关联,说明市区LU延续性好,是市区土地发展成熟的体现。模式分析结果如表2所示。

表2 7号线LUC规律BN模式分析Table 2 Pattern analysis for BN of 7 Line
表2 中,区域变量取为缓冲区时,强度较大的变量依次是初始邻域田地地块个数、森林、建筑用地个数。表明缓冲区与参照区上述变量出现了显著差异,初始邻域田地、森林地块个数与上文分析一致。初始邻域建筑地块个数解释同初始邻域森林地块个数变量。
(3)网络推理与预测
针对多摩线,初始态变量取为建筑,区域变量取为缓冲区,初始邻域建筑个数取为0 个时,06 终态变量为建筑用地的概率P(06 终态=建筑/初始态=建筑,区域=缓冲区,建筑=0)为52.8%,如图7所示。据此,针对建筑用地的推理内容如图8所示。

图7 多摩线LUC规律BN推理示意图Fig.7 Chart of BN Inference for Tama Line

图8 多摩线建筑用地BN推理内容Fig.8 BN inference for construction land of Tama Line
从图8看出:
(1)对比a1与a2,缓冲区组06终态为建筑用地的概率随着初始邻域建筑用地个数的增加而增大,但是幅度很小(52.58%~54.47%),趋平缓;参照区组增大的幅度较明显(5.8%~64.35%),且0到1还有较大的跨越,说明参照区建筑地块邻域无建筑地块时,该地块终态为建筑用地的概率非常小,但当邻域有建筑地块时,该地块终态为建筑用地的概率变得非常大,反映了参照区建筑地块聚集程度较高。b1与b2对比也有同样的规律。
(2)对比a1 与b1,a2 与b2 可看出,无论地块位于缓冲区还是参照区,初始态为建筑用地,06 终态为建筑用地的概率均大于初始态为森林的情况,且参照区较明显,说明参照区初始建筑地块带动邻域开发为建筑地块的程度要大于缓冲区,同样也反映了参照区建筑地块聚集程度较高。
(3)对比c1与c2可看出,无论地块位于缓冲区还是参照区,无论其初始邻域建筑用地个数大小,初始态为建筑用地,97终态为建筑用地的概率始终非常高,这与前述97 终态与初始态有直接关联一致。而d1 与d2 也论证了此结论,当初始态为森林用地,无论地块位于缓冲区还是参照区,无论其初始邻域建筑用地个数大小,97终态为建筑用地的概率始终非常低。
与(1)和(2)中郊域线运营期参照区建筑地块聚集程度较高相比,缓冲区地块演变为建筑用地受建筑用地聚集程度影响较低,演变较独立,同样是由郊域线作为强驱动力,引起LUC 活跃程度比较大引起的;此外,还可推理出当06终态变量选为建筑用地时,区域变量为缓冲区的概率为87.2%,初始邻域森林个数取为0 个的概率为98.5%,说明为支持06终态变量为建筑用地,区域需在87.2%的概率为缓冲区,初始邻域用地需98.5%程度上为非森林地块。
基于BN 推理可预测未来LU。以多摩线2006年LU 作为初始态,根据运营期1997—2006年LU数据标定BN,进而预测2014年LU。总地块数为6539 个,预测结果与实际地块不相符的个数为654,预测精度达89.9%,结果如图9所示。

图9 多摩线缓冲区LU预测Fig.9 Prediction of LU for Tama Line
2.4 轨道交通引起的LUC机制
既有文献对交通设施引起的LUC 机制的解释均归结于交通自身的功用——提高出行可达性[13-17]。文献[13-14]中,因为可达性提高,在道路网络发展至不仅使车辆到达种植地比较便利同时,旱地作物被运往市场也很便利,旱地作物用地对道路网络这个因素十分敏感,典型的LUC 现象是森林退化为旱地作物耕地;同时道路网络连接度越好,建筑用地比例越高,说明人们更偏好在道路网络附近定居以获得较好的可达性。轨道交通的建设使得人们出行可达性提高,吸引人们愿意在其周边居住与生活,因此出现居住商业等用地以及密度增加等现象。据此分析郊域线LUC 的表现,郊域线运营后极大提高缓冲区内居住与商业出行的可达性,会受相关用地如建筑用地的青睐,故其缓冲区与参照区LUC出现了明显差异。同样也会导致缓冲区地价上升,使得工业迁走,森林农田被开发等;在某些用地类型消失,新的用地类型出现的过程中,用地类型更迭显著,即表现出运营期与前期LU 无直接关系;因为建筑用地受到青睐,即使邻域没有建筑地块,其他用地突变为建筑地块的可能性也较大,表现出运营期缓冲区地块演变为建筑用地受建筑用地聚集程度影响较低。
但是在文献[13-15]中,均提到交通设施并不是引起LUC的唯一因素,诸如社会经济、政策等均会影响LUC,这一方面说明了参照区与缓冲区设置的合理性,另一方面也佐证了市区LUC 多驱动力的解释,因为在一个城市中,市区总是因为拥有大量就业岗位以及商业娱乐活动频繁导致其吸引力更强,社会经济与政策因素都会向市区倾斜,因此市区比郊区拥有更多的LUC 驱动力,即便是轨道交通线网也十分密集,市郊线参照区LUC 会受到其他驱动力的影响而使得演变与缓冲区无差异。
3 结论
随着郊区新型城镇化的推进,郊域线的建设是必要可行的。为探索郊域线与土地利用之间的关系以促进两者协调发展,针对郊域线的LUC 规律进行研究。采用与LUC 特征描述较为符合的BN模型分析郊域线LUC 机制,探讨了影响LUC 的因素——地块初始态、初始邻域地块状态、地块所处区域对LUC 的影响,在既有研究多以市郊线为对象并主要对LUC 结果进行简单统计的现状下,丰富了轨道交通LUC机制研究。本文得到主要结论如下:
(1)郊域线开通前后参照区与缓冲区LUC出现显著差异,其对LUC产生了明显影响;市郊线则未产生影响。综上说明不同于市区LUC 的多驱动力,郊域线作为郊区LUC的强驱动力,引起的LUC变化显著,故通过建设郊域线推动郊区土地发展,加速郊区新型城镇化进程是可行的。
(2)BN推理显示,郊域线运营期缓冲区终态为建筑受建筑用地聚集程度的影响低于参照区,演变较独立,可为郊域线土地开发过程中建筑用地布局提供参考。为支持郊域线运营期地块终态为建筑用地,区域需87.2%的概率为缓冲区,初始邻域用地需98.5%程度上为非森林地块,可为郊域线土地开发过程中建筑用地选址提供参考。
(3)多摩线缓冲区2014年LU 预测结果精度为89.9%,表明BN较强的推理能力,论证了选用贝叶斯网络分析郊域线LUC机制方法的有效性。
本文仅将区域变量设为缓冲区与参照区衡量郊域线对LUC 的影响,但缓冲区内到车站不同距离区域LUC 是否差异显著是进一步研究的方向。
