初中数学思想传授谈
2021-08-26毕宝清
毕宝清
摘 要:初中数学教学不仅是对数学知识进行教学,还是对数学思想方法的教学。文章作者认为,教师在教学中可从两方面入手:一方面,通过数学思想的渗透,启发、帮助学生发现和认识教科书中阐述的数学方法,使数学教学不是单纯的知识灌输,而是使这些方法成为分析问题和解决问题的有力工具,做到自然而然地掌握和运用;另一方面,通过对数学方法的掌握,进一步了解隐含于其中的数学思想,认识到具体事物的本质,从而逐步掌握科學的思想方法。
关键词:初中数学思考;方程思想;分类思想;数形结合思想
中图分类号:G633.6 文献标识码:A 文章编号:2095-624X(2021)23-0051-02
初中数学教学不仅是数学知识的教学,更重要的是数学思想方法的教学。《义务教育数学课程标准(2011年版)》已经把“双基”扩展为“四基”,即增加“基本数学活动经验”与“基本数学思想方法”,突出数学思想方法的教学,是当代数学教育的必然要求。
数学思想方法是数学基础知识的重要组成部分,它反映了数学的本质特征,是对数学概念、原理和方法的本质认识,是分析和处理数学问题的指导思想。初中数学学科具有其自身的思想方法,它所体现出来的数学思想主要是指方程思想、函数思想、数形结合思想、转化思想、分类思想、集合思想、统计思想等。数学思想具有本质性、概要性、指导性的意义,是人们分析、解决数学学科问题过程中思维活动的导航器。数学方法是人们学习、应用数学知识的思维策略或模式。数学思想和数学方法有密切的联系,思想是内含的,方法是外显的,思想融于知识中,通过方法来表现,方法的内核是思想,它以思想为指导,又可升华为思想。数学思想和方法隐含于现成的结论和说明中,这就需要我们在教学中,不能只停留在对教材表现的结论和说明的表述上,不能只盯住解题、做题,而应向学生传授数学思想方法,提高他们分析和处理问题的能力。下面主要介绍初中数学中几种重要的数学思想和方法。
一、方程思想
所谓方程思想,是指在求解数学问题时,从题中的已知量和未知量之间的数量关系入手,找出相等关系,运用数学符号语言将相等关系转化为方程(方程组),再通过解方程(组)使问题得以解决。方程思想是中学数学中非常重要的数学建模思想之一,其应用十分广泛。解题过程通常是:首先,从整体上分析题意,确定未知量的个数;其次,适当选择一个或几个未知量用x(或y, z……)表示,并弄清它(它们)与其他未知量的关系;再根据题设中的条件,列出方程(组),并求解。
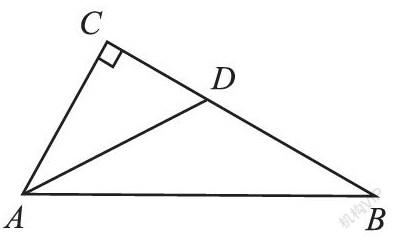
例1:在直角三角形ABC中,AD是∠BAC的平分线交BC于点D,且CD=3,BD=5,∠C=90°,求AC的长。
教师通过此题可以向学生介绍,如何利用勾股定理列方程,即传授方程思想。
又如,一个角的余角比它的补角的1/3还少20°,求这个角。
解析:先设这个角为x 度,则根据题意,得到关于x 的方程:
90°﹣x + 20°=1/3 (180°﹣x )
解得 x=75°。
运用方程思想,这类问题就会变得简单明了。
二、分类思想
所谓分类思想,一般是指解决问题时,将错综复杂的若干问题,按逻辑学规律,将问题逐一梳理规划,排列分类,采用不同的方式分析研究的一种正向思维。
在运用分类思想处理问题的关键是把握分类的标准,保证分类的科学性和合理性,分类要达到互斥、不漏、不重、最简的要求。
运用分类思想解题的过程中,要同中求不同(一个命题分成几种不同的类型);不同中求同(几种不同类型的研究结果综合成命题的一个完整答案)。
在解题时,根据已知条件和题设的要求,分不同的情况做出符合题意的严谨、周密的解答。
例2:已知三角形的周长小于13,且各边长为互不相等的整数,则这样的三角形共有( )。
A.2个 B.3个 C.4个 D.5个
分析:本题是要考查分类思想方法,解题中要对周长小于13的整数分别讨论,同时还要注意隐含条件“三角形两边之和大于第三边”,从而根据不同情况对问题做出全面解答,结果是以5、4、3和5、4、2及4、3、2为边的三角形符合条件,故选B。
在分类的时候,教师应鼓励学生按多种类别分类,并进行讨论交流,这样,一方面可给学生提供主动参与的机会,把学生的注意力和思维活动调节到积极状态;另一方面可培养学生思维的灵活性,加速体现分类的思想方法。在平时的训练中,我们要多通过这类题向学生传授分类讨论的思想。通过分类讨论,既能使问题得到解决,又能使学生学会多角度、多方面去分析、解决问题,从而培养学生思维的严密性、全面性。
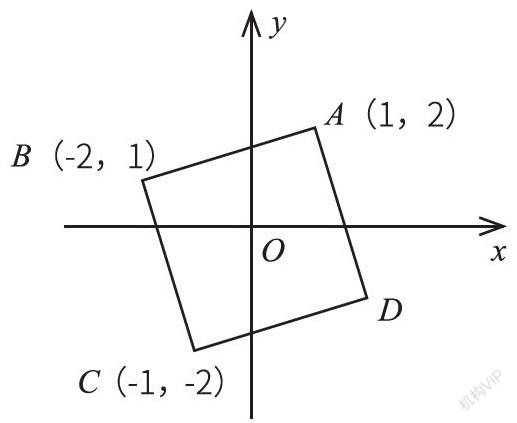
三、数形结合思想
数形结合思想是指将数与图形结合起来解决问题的一种思维方式。数学是研究现实世界空间形式和数量关系的科学,因而,在某种程度上可以说数学研究是围绕数与形展开的。初中数学中的“数”就是代数式、方程、函数、不等式等符号表达式,初中数学中的“形”就是图形、图像、曲线等形象的表达式。数形结合思想的实质是将抽象的数学语言“数”与直观的图像“形”结合起来,数形结合思想的关键就是抓住“数”与“形”之间本质上的联系,以“形”直观地表达“数”,以“数”精确地研究“形”,实现代数与几何之间的相互转化。数形结合思想包括“以形助数”和“以数辅形”两个方面,它可以使代数问题几何化,几何问题代数化。著名数学家华罗庚曾经说过:“数缺形时少直观,形少数时难入微。”这就是在强调把数和形结合起来考虑的重要性。通过图形,探究数量关系,再由数量关系研究图形特征,使问题化难为易,化形象为直观,从而解决数学问题,这是一种重要的数学思想方法。数形结合思想是研究数学、解决数学问题的重要思想,在初中数学中有着广泛应用。
