非周期长码直扩信号同步及伪码序列盲估计

邱钊洋 李天昀 查 雄

(信息工程大学信息系统工程学院 郑州 450001)

1 引言

直接序列扩频体制是指在发送端采用伪随机序列对发送符号进行调制，从而提高信号抗干扰性能的一种通信体制[1]。该体制的核心思想是用发射带宽换取发射功率，理论上只要伪码长度足够长，可实现任意倍数的扩频增益。由于伪随机序列具有类白噪声特性，DSSS信号具备显著的抗干扰、抗截获能力，因此广泛运用于军用和商用通信系统，如GPS系统、联合战术信息分发系统、NTDR高速数据电台等[2–5]。对此类信号开展非合作接收条件下盲解调技术的研究，在军事通信对抗、频谱侦察及无线电管控等领域都具有十分重要的意义。

通常，根据伪码周期和信息码周期之间的倍数关系，DSSS信号可分为3类：当伪码周期与信息码周期相等时，称为短码直扩信号(SC-DSSS)；当伪码周期为信息码周期的整数倍时，称为周期长码直扩信号(PLC-DSSS)；当伪码周期大于信息码周期且二者无倍数关系时，称为非周期长码直扩信号(NPLC-DSSS)。针对SC-DSSS和PLC-DSSS信号伪码盲估计问题已经有较为成熟的方法，如特征值分解[6,7]、神经网络[8,9]、聚类方法等[10,11]，但由于NPLC-DSSS信号中伪码被信息码随机扰乱，难以直接应用上述方法。

现有的针对NPLC-DSSS信号伪码估计问题的方法主要包括分段特征值分解法[12]、差分特征值分解法[13]等，其中分段特征值分解方法主要思想是将信号划分为一系列重叠的时窗，然后建立多个自相关矩阵进行分段估计，最后将得到的分段估计进行拼接，这种方法假设小时窗长度内信息符号不发生跳变，从而相当于多个SC-DSSS的估计问题，但这种方法存在时窗分辨率与性能之间的矛盾。差分特征值分解法的主要思想是对接收信号进行差分以消除发送波形调制的影响，然后进行周期分段特征值分解，这种方法简单易行，但时域差分操作降低了信号的信噪比，导致性能欠佳。文献[14]采用相似性度量指标，通过遍历信息符号，实现了失步时间与伪码的联合估计，这种方法在高信噪比条件下性能优良，但信号质量较差时，性能退化严重，同时算法复杂度较高，当伪码周期远大于信息码周期时将难以应用。文献[15]采用等效周期(伪码周期和信息码周期的最小公倍数)对差分后信号进行周期分段，并沿用特征值分解方法，这种方法简单有效，但伪码周期与信息码周期二者互质时，等效周期过大导致特征值分解的复杂度大大提升，难以工程实用。多通道接收条件下的NPLC-DSSS信号伪码序列估计也得到了一定程度的关注[16]，但要求多个天线阵元，不适用于单通道NPLC-DSSS信号处理。实际中迫切需要一种简单高效的NPLC-DSSS信号伪码估计方法，以应对多变的信号的体制。同时，考虑到对现有算法的评估大多采用误码率指标，存在下界的不准确性，因此对伪码估计问题的理论界进行研究显得十分必要。

本文通过研究NPLC-DSSS信号的时序特性，依据相关矩阵中元素分布提出一种信息码宽分段方法，并根据相关矩阵Frobenius范数与失步时间之间的关系实现了NPLC-DSSS信号失步时间估计和基于判决辅助的高性能伪码估计算法。同时，通过对NPLC-DSSS信号伪码盲估计问题的理论界开展了深入的研究，推导了参数Fisher信息矩阵(Fisher Information Matrix,FIM)[17]及正定约束条件，给出了约束的Cramer-Rao界并对该理论下界的合理性和准确性进行了分析。

2 信号模型

假设接收信号已完成载波同步和定时同步，伪码周期及信息码宽已获得精确估计[18,19]，基带BPSK调制的NPLC-DSSS信号可表示为

由式(3)，式(4)可知，若要准确地描述信号结构，需要已知失步时间τ。一般情况下，非合作方接收信号起始位置随机，故首先需要完成对失步时间τ的估计。其次，在对随机发送的信息码无先验知识的条件下，对扩频序列进行估计。本文提出采用以信息码宽长度分段下平均自相关矩阵的Frobenius范数准则，以实现NPLC-DSSS信号的盲同步，并在此基础上通过引入判决辅助思想，实现了高性能的伪码序列的迭代估计。

3 算法设计

3.1 基于信息码宽分段的失步时间估计方法

针对SC-DSSS及PLC-DSSS信号，基于相关矩阵Frobenius范数最大化的失步时间估计方法是一个较优的选择。该算法首先将数据依次按伪码周期长度进行分段，并求取平均的自相关矩阵。文献[20]的分析表明，在渐进意义上，该自相关矩阵的Frobenius范数在SC-DSSS信号恰好同步时(τ=0)达到最大。PLC-DSSS信号与SC-DSSS信号具有类似的结构，因此这种方法在PLC-DSSS信号的失步时间估计中也显现出较好的效果。而NPLC-DSSS信号中伪码序列受到发送符号的随机调制，破坏了周期内的符号取值累加特性，使得基于伪码周期分段的Fr obenius范数的失步时间估计方法对NPLCDSSS信号并不适用。

通过对矩阵Frobenius范数思想的理论分析，提出一种基于信息码宽长度分段的NPLC-DSSS信号分段方法，对分段后的自相关矩阵计算Frobenius范数可实现高性能失步时间估计，从而避免符号随机调制对失步时间估计的影响。下文对此展开详细讨论。的发送符号窗口，pj,m p j,n将 等概率地取得±1，此时多分段累加后互相抵消，导致R L1(m,n)趋近于0。因此，按照伪码周期对NPLC-DSSS信号进行分段，伪码周期大于符号周期将导致P矩阵元素取值离散化，使得自相关矩阵难以呈现区分度。

根据NPLC-DSSS信号的机制，若以信息码周期进行分段，当起始分段位置为信息码波形跳变点时(与失步时间等效)，式(6)中pj,m,p j,n将位于同一发送符号下，有pj,m p j,n=1，相关矩阵实现同号累加；反之不同步时，p j,m p j,n取值将发生离散，根据m,n之间的距离依概率取得1或–1。此时，部分矩阵元素叠加过程中相互抵消，导致矩阵范数减小。失步时间不同，p j,m p j,n取值离散的程度也不相同，基于此可有效识别出NPLC-DSSS信号的失步时间。

当失步时间为τ，以信息码宽长度G分段的NPLC-DSSS信号平均分段自相关矩阵可表示为

3.2 NPLC-DSSS信号伪码序列估计

步骤4通过式(13)求得伪码序列估计，并求得式(14)所示的当前代价函数值；

步骤5判断模型的收敛性，即考察当前代价

R G,ττG=60,L=1500,M=2000

图2 RG矩 阵Frobenius范数随失步时间τ 的变化(G=60,L=1500,M′ =2000)

图1 中元素取值分布与不同时延 的关系( )函数值与上一轮迭代过程的代价函数值相等时，认为算法收敛，转步骤7，否则转步骤6；

步骤6采用步骤4估计所得的伪码序列对信号进行相关解调并进行硬判决，获得当前发送序列，转步骤4；

步骤7多次重复步骤3至步骤6，选择模型收敛时代价函数值最小的一次迭代结果对应的伪码序列作为信号伪码序列的最终估计。

4 伪码估计理论界

对于NPLC-DSSS信号伪码估计问题，已有算法的性能评估大多以伪码估计或信息码解调误码率为指标进行对比，虽然一定程度上可反映算法性能的优劣，但存在不合理性及算法性能下界的不确定性。误码率指标通常对信号解调而言，实际上是信息码估计问题。而盲估计问题由于伪码与信息码均未知，实际上是联合估计问题，故仅用误码率指标难以反映真实的理论界。下文拟对此问题展开分析，推导该联合估计模型中伪码估计的理论下界。

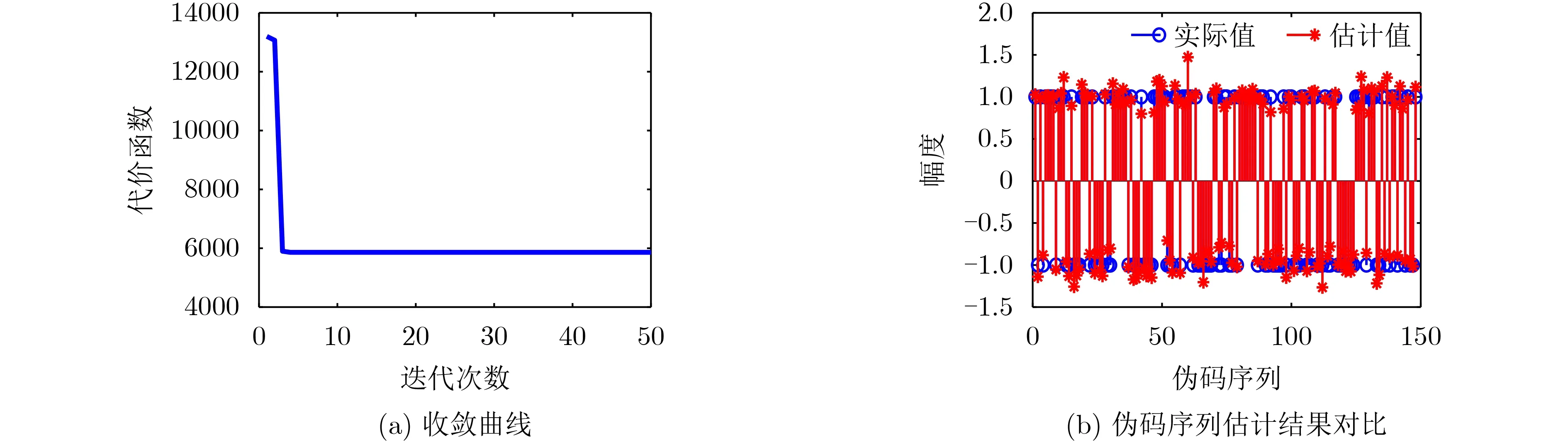
图3 基于判决辅助的伪码盲估计结果

图4 NPLC-DSSS信号同步及伪码盲估计流程

文献[21]指出，约束CRB由梯度的矩阵的零空间对FIM矩阵进行正则化给出。最小约束CRB可由式(25)得到

5 仿真实验及性能分析

5.1 Cramer-Rao界分析

本节将考察上文中推导Cramer-Rao界的合理性及相关影响因素，以更好地作为参考界评估算法性能。虽然第4节所提Cramer-Rao界主要针对NPLC-DSSS信号，但实际上SC-DSSS与PLC-DSSS信号均可视为NPLC-DSSS信号的特殊情况。故本节中Cramer-Rao界合理性主要通过其在特殊情况下的取值与已知信息码条件下的CRB对比进行分析评估。同时，考察了不同伪码周期及信息码宽对CRB的影响以揭示可能影响估计性能的参数。实验信号的数据量均为30个伪码周期。图5显示了不同参数下CRB的对比。

理论上而言，由于未知的信息增多，盲估计的性能应低于或等于非盲估计性能。图5(a)中，各参数条件下SC-DSSS及PLC-DSSS信号盲估计与非盲估计的CRB曲线重合。同时，SC-DSSS(L=15,G=15) 与PLC-DSSS(L=60,G=15)信号的伪码盲估计与合作估计4个理论界重合，说明周期长码的CRB只与扩频因子G有关，而从信号模型而言，PLCDSSS信号恰为多个SC-DSSS信号的组合，理论界的贴合符合二者之间模型的等价性。单独考察SCDSSS时，其理论界随着伪码周期L的增加而上升。综合SC-DSSS及PLC-DSSS信号来看，由于扩频因子决定了范数约束长度，当序列较长时，范数约束的影响对于每个码比特将减弱，导致CRB升高。实验结果与理论分析对应，说明了所提CRB的合理性。

图5 不同信号参数下CRB对比

图5(b)展示了3种不同参数下NPLC-DSSS信号伪码估计理论界对比。可见，对于NPLC-DSSS信号，伪码盲估计CRB相比非盲估计CRB略有升高，符合实际情况。同时，与图5(a)结论相似，NPLC-DSSS信号伪码盲估计CRB主要与扩频因子G有关，与伪码周期关系甚微。

5.2 伪码估计算法性能

为衡量所提基于判决辅助的伪码估计算法性能并进一步验证CRB的合理性，选取了两种不同参数下NPLC-DSSS信号进行算法性能测试，其参数如表1所示，其中伪码序列选用m序列或截断m序列。其估计的NMSE分别如图6、图7所示。

表1 实验信号参数

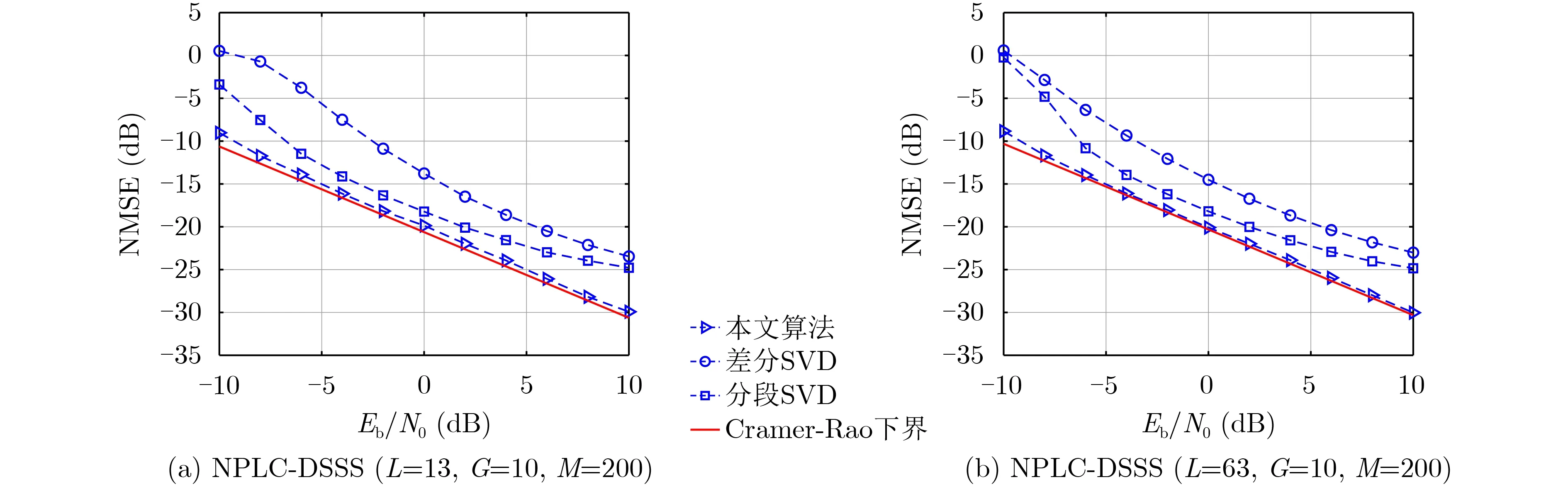
图6 估计性能随信噪比的变化

图7 估计性能随数据量的变化

图6展示了算法的抗噪声性能。由图6(a)对比可见，所提算法在实验信号参数下信噪比为–5 d B左右即可贴近理论界，在各信噪比下均优于差分特征值分解和分段特征值分解方法。图6(b)展示了伪码周期与信息码周期比值较大的情况，所得结果与图6(a)保持一致，说明了伪码周期的大小对算法性能没有影响，证明了算法的鲁棒性。

图7展示了算法性能随数据量的变化。对比可知，信噪比为–5 d B，数据量在80个伪码周期左右时，所提算法性能即可达到理论界。相比而言，差分方法在此信噪比下，性能较差，本文算法比分段方法也有2～3 d B的性能提升，说明了算法的优势。

6 结束语

本文主要研究了NPLC-DSSS信号失步时间及伪码序列盲估计问题，通过对信号相关矩阵的讨论，构建了基于信息码宽分段相关矩阵Frobenius范数的盲同步方法，实现了失步时间估计。根据估计所得参数建立信号模型，基于最大似然判决辅助理论设计了迭代估计结构，实现了高性能伪码盲估计。最后针对伪码盲估计问题推导了参数估计理论界，并通过仿真实验证明了所提算法的优良性能。值得一提的是，基于判决辅助思想不仅在单用户DSSS信号伪码估计问题中展示出出色的性能，在多用户及多速率DSSS信号伪码估计问题中也具有广阔的应用前景。