基于能量算子和最大旁瓣衰减自卷积窗函数频谱校正的电压闪变参数识别技术及其在风电场的应用研究
2021-08-26邱衍江张新燕王维庆
邱衍江 张 超 张新燕 王维庆
①(澳门科技大学资讯科技学院 澳门 999078)
②(广东电网有限责任公司广州供电局 广州 510620)
③(可再生能源发电与并网技术教育部工程研究中心(新疆大学电气工程学院)乌鲁木齐 830047)
1 引言
近些年以风能等为代表的新能源发电技术因性能优良而在电网中运用不断加深,但其固有波动性在并网时会产生电压闪变与电压波动,严重影响电网电能质量[1,2]。另外,风力发电技术中所用的静止无功补偿器(Static Var Compensation,SVC)、静止无功发生器(Static Var Generator,SVG)等容性无功补偿设备同样会导致上述问题,给工业生产和日常用电造成不可忽视的重大影响[3,4]。故需要针对规模化风电并网地区研究一个针对性强且准确性高的闪变参数检测法。
当前智能电网背景下电网波形畸变严重,且由于人眼对矩形波调制下的闪变更为敏感,因此亟需对矩形波调制下的闪变参数识别开展深入研究。针对电压闪变包络两大参数的准确识别提取,现有方法主要包括HHT(Hilber-Huang Transform)法[5,6]、小波变换法[7,8]、S变换法[9]及快速傅里叶变换(Fast Fourier Transform,FFT)法等算法。FFT参数检测准确度高且计算处理量小,但谱间泄露和栅栏效应会严重影响电压闪变参数识别精度[10]。为提高非同步采样下的分析精度,一般采用莱芙-文森特(Rife-Vincent,R-V)截断窗、Kaiser截断窗等对信号加权以克服频谱泄露,采用插值校正法克服栅栏效应[11]。
本文首先对矩形方波调制下的传统算子的采样间隔进行优化以提升其抗噪能力和谱追踪能力,构建出更适用于工况变化较快的风电汇集地区包络提取求解法。其次,基于余弦窗函数的归一化对数谱,本文选用通过遗传算法改进的6项余弦组合窗为原始窗构建最大旁瓣衰减自卷积窗(Maximum Side-lobe Decay Self-Convolution Wind ow,MSLD-SCW)函数。通过频域特性分析,综合主瓣特性与旁瓣特性等指标,选择2阶MSLD-SCW函数对信号做截断处理。基于三谱线参数信息校正原理并利用Matlab中的polyfit函数推导出2阶MSLDSCW函数的拟合修正公式,将其运用于闪变包络的幅值与频率两大参数识别与估计。通过与设置对照组算法的仿真结果对比,验证改进优化算法精度较高。
最后,将所提算法运用到新疆某地区电网实际的电压闪变参数检测中,能够高精度地实现检测目标,具有很高的实用性。
2 电压闪变数学模型
现有电压闪变的仿真研究模型多是基于如式(1)所示的数学表达式
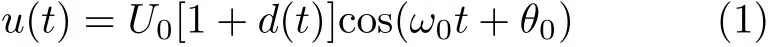
式(1)中是以[0.05 Hz,35 Hz]的正弦波函数为调制分量,d(t)为闪变量表达式,U0,ω0,θ0分别代表基波电压幅值、频率量与初相位。
但当前智能电网背景下电网波形畸变严重,且矩形波调制下的闪变对人眼更为敏感,故本文以新能源并网地区为研究背景,矩形波信号的离散表达式为

式(2)中Wrect(·)为矩形截断窗离散表达形式,其傅里叶级数可以通过式(3)表示;Ωi=2πfi/fs;l为矩形波信号分量的项数;ki与fi是第i项调幅波的幅值与频率两大调制系数;f0为电网基波频率;fs为信号采样频率。
3 能量算子包络提取
3.1 传统Teager能量算子
因风电汇集地区电网工况变化迅速,精准且分析迟延短地进行闪变包络分析提取是实现闪变两大参数高精度识别的前提,能量算子可以仅通过信号中3个相邻的离散采样点反映出瞬时能量变化情况,且实现简单快速。
对于连续信号x(t)的能量算子可以表示为

其中,x′(t),x′′(t)分别表示信号x(t)的1阶导及2阶导。

设x(t)的离散表达式为x(n),则其能量算子定义为其中,离散采样点n的左右邻近采样值分别以n+1和n–1表示。
离散信号x(n),y(n)的乘积的能量算子为

对于传统能量算子法,采用文献[12]的推导过程与结果,闪变包络d(n)表达式可近似表示为
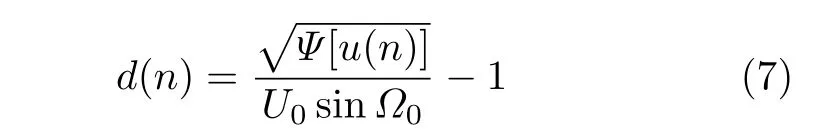
3.2 改进能量算子包络提取
能量算子提取精度易受噪声环境的影响,本文提出增加采样间隔的改进Teager能量算子包络提取方法,即使式(5)的采样间隔加1,以使闪变信号特征值变化的追踪能力得以提升,表达式为
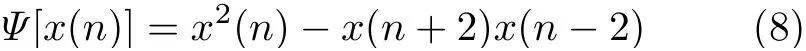
将式(2)代入式(8)中,可得基于优化改进提取方法下的包络信号表达式为
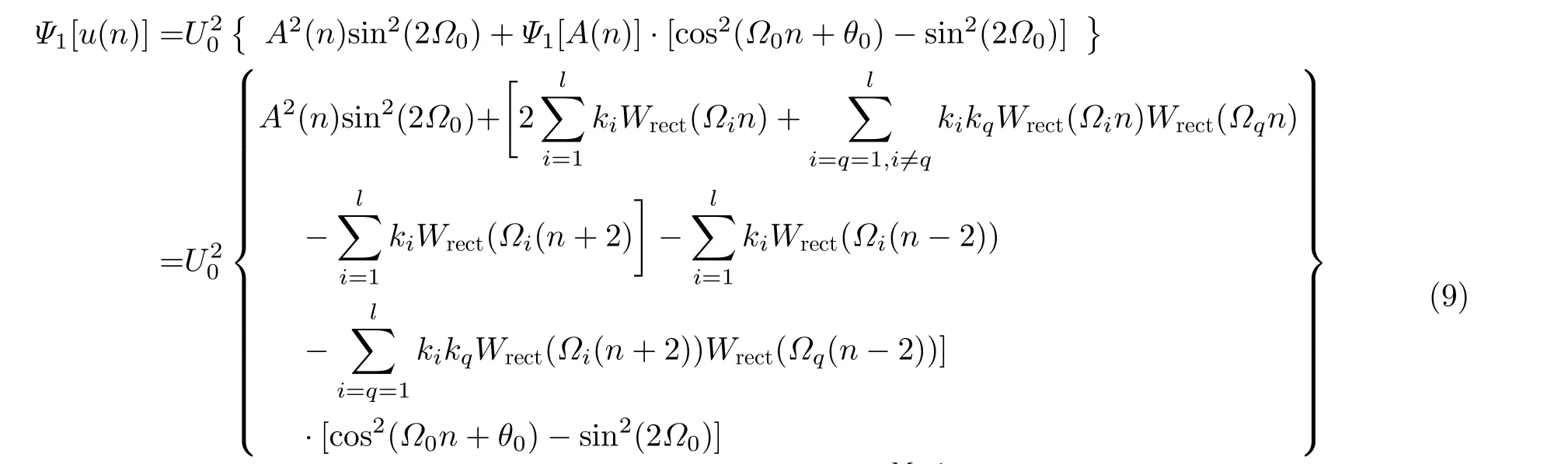
忽略式(9)中的较小部分,仅保留式中主项分量,则采用改进能量算子闪变包络分量为
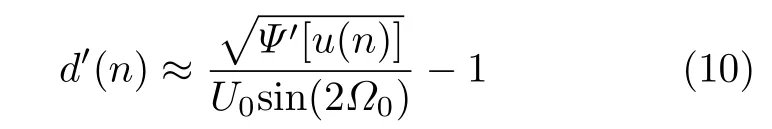
设置基频仿真参数值为50 Hz,fs为800 Hz,矩形调制信号频率为10 Hz,幅值为0.01 p.u.,图1为运用两种算法的包络提取分量结果。由图1可知,基于传统算法得到的矩形波包络会在矩形信号上升沿与下降沿处产生较大的误差,而本文优化改进后的能量算子可以有效提高包络提取精度。
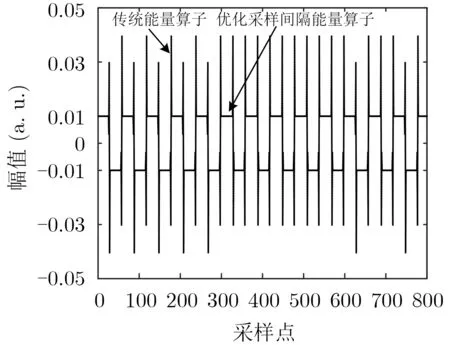
图1 基于传统和优化改进算子的包络提取对比分析结果
4 基于加MSLD-SCW函数插值FFT闪变参数识别算法
4.1 新型MSLD-SCW函数
余弦窗的时域表达式及其DFT形式如式(11)和式(12)所示
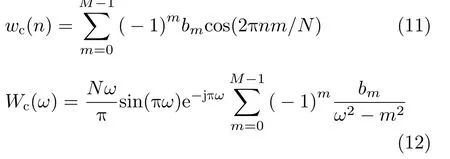
其中,M为窗函数项数,bm为窗函数系数。
因包括旁瓣峰值水平及旁瓣衰减速率在内的旁瓣性能制约着窗函数克服频谱泄露的能力,文献[13]以旁瓣性能为参数优化的目标,利用遗传智能算法对经典6项余弦截断窗的系数bm进行优化,得到MSLD组合余弦截断窗。图2为典型余弦截断窗与MSLD函数的幅频响应曲线,相比于其他余弦窗,优化改进MSLD窗旁瓣性能更加突出,以其为原始母窗构建MSLD-SCW函数能更好地减小闪变参数识别中的频谱泄露。
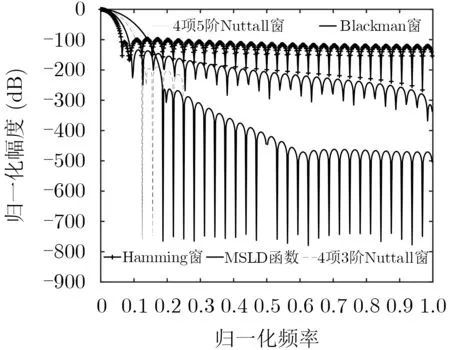
图2 MSLD函数与经典截断窗的归一化幅度曲线
设wMSLD-p(L)是以改进的M SLD截断窗wMSLD(L)为母窗得到的p阶SCW函数。由卷积定理可知,p阶MSLD-SCW函数频域表达式为式(14)
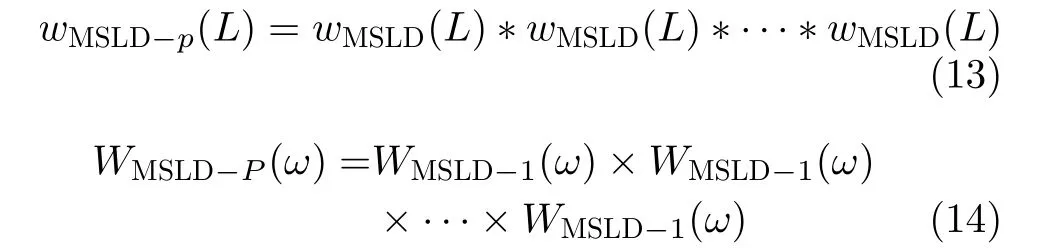
图3给出了2阶及4阶MSLD-SCW函数,以及p=2时的Hamming卷积截断窗(H-SCW)函数、4项5阶Nuttall卷积截断窗(N-SCW)的归一化幅度谱,其中N=128。
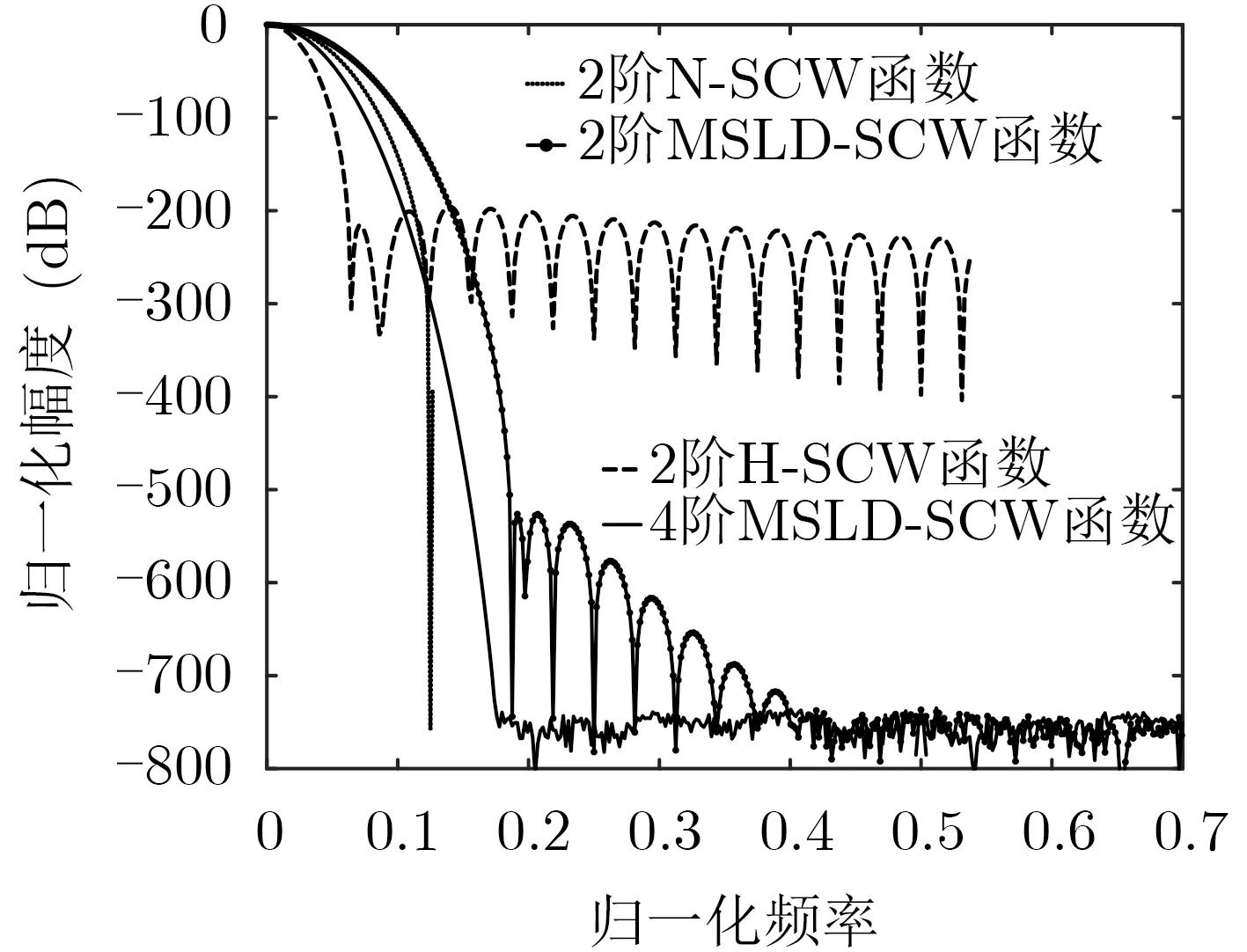
图3 几种自卷积截断的幅度谱
由图3可以得出,不失一般性地,SCW函数相比于原始母窗频域性能均有提升,且母窗项数M越大,SCW函数的旁瓣性能改善越明显。另外,主瓣宽度也会随之增加,导致降低了频率分辨率,且运算量也将成比例增大。综合考虑,采用2阶MSLD-SCW函数对信号加权截断,以抑制频谱泄露对检测精度的影响[14]。
4.2 基于2阶MSLD-SCW函数的插值校正
用2阶MSLD-SCW函数wMSLD-2(n)对d(n)进行加权截断处理,并做DFT运算,则信号的谱函数如式(15)所示
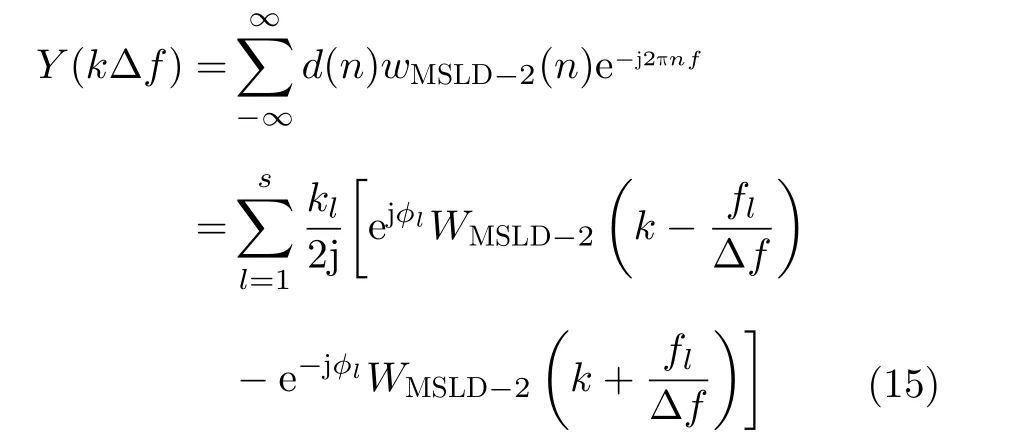
其中,k=0,1,···,N–1; Δf=fs/N;kl与fl代表第l项调制波的幅值与频率两大调制系数;WMSLD-2(·)为2阶MSLD-SCW函数的频谱函数。
为方便分析推导,忽略负频点处频峰的旁瓣影响,取第l次信号幅值如式(16)所示

将式(17)和式(18)代入式(19),可得
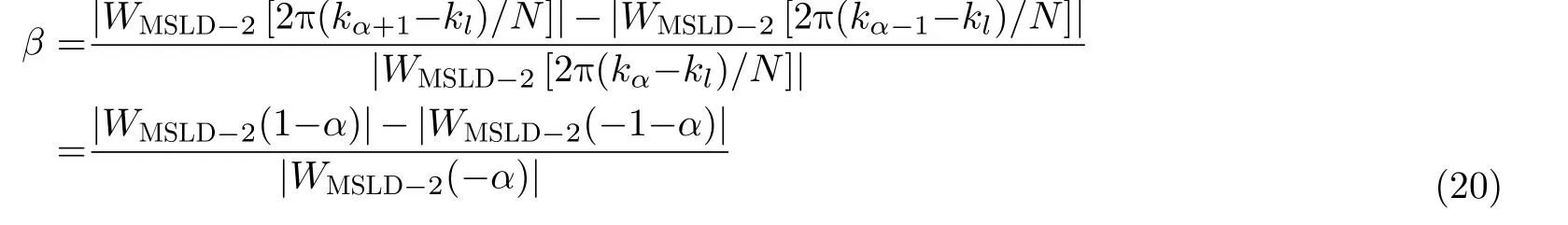
在[–0.5,0.5]取1组数据,代入式(21)可得1组β,利用Matlab中polyfit(β,α,7)函数对式(20)进行反拟合,可得频偏表达式如式(21)所示
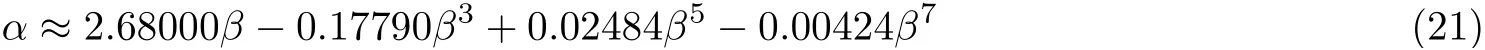
对参数kl进行校正时,考虑到最大幅度谱kα富含关于闪变参数信息,故给予其较大的权值系数,具体地
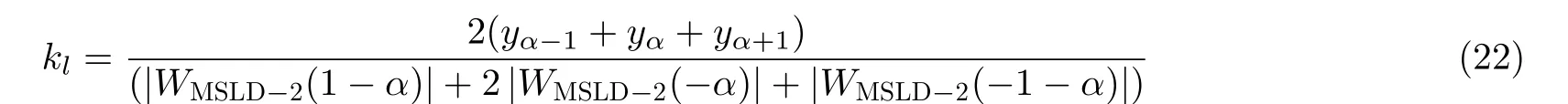
当N远远大于1时,式(22)可简化为
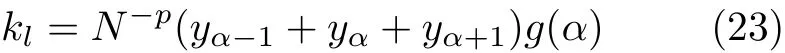
采用相同的取值代入求解法,并运用polyfit(α,g(α),7)函数进行正拟合,即可得到g(α)的拟合公式如式(24)所示
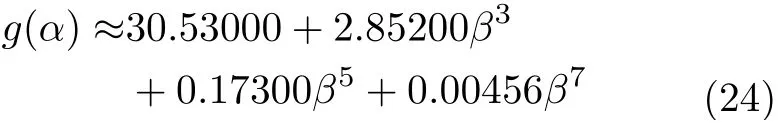
5 仿真实验分析
5.1 单频闪变包络调制

由图4和图5结果可见,当闪变调制波形中仅含单一频率包络成分时,除固有误差峰值点25 Hz闪变外,基于改进优化参数识别方法的ml相对误差处于10E-2%~10E-4%数量级,fl的相对误差为10E-3%~10E-6%数量级,满足国际电工委员会(International Electro technical Commission,IEC)中关于《闪烁仪的功能和设计规范》的误差要求。且本文参数识别法的提取精度相比于对照组算法有了显著提高,如针对fl为11 Hz时的闪变参数提取,基于传统算法的ml及fl识别相对误差为1.438%及0.167%,而基于本文算法的相对误差为6.36E-4%及5.32E-6%,改善效果明显。
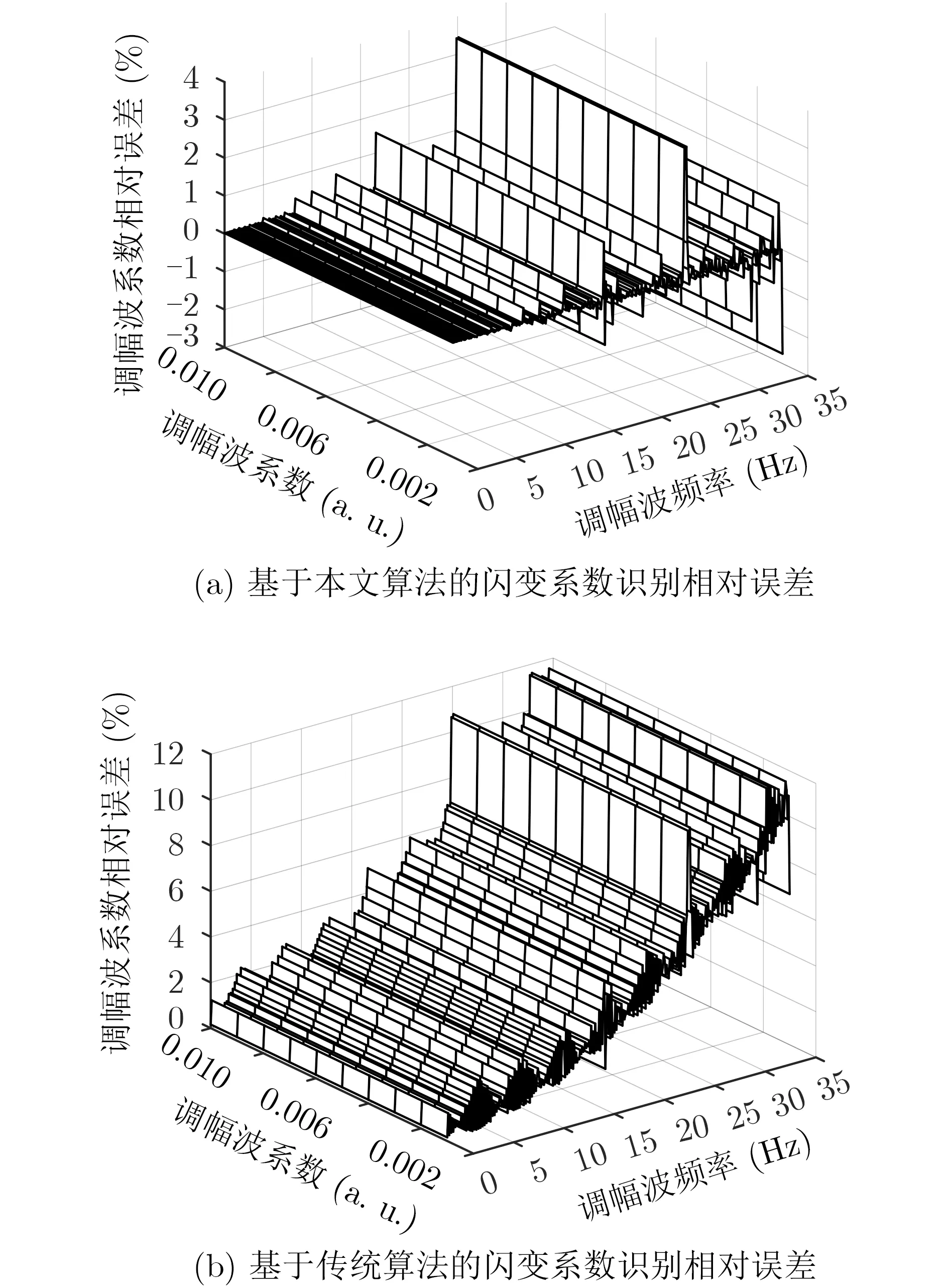
图4 单频调制分量时的闪变系数识别误差
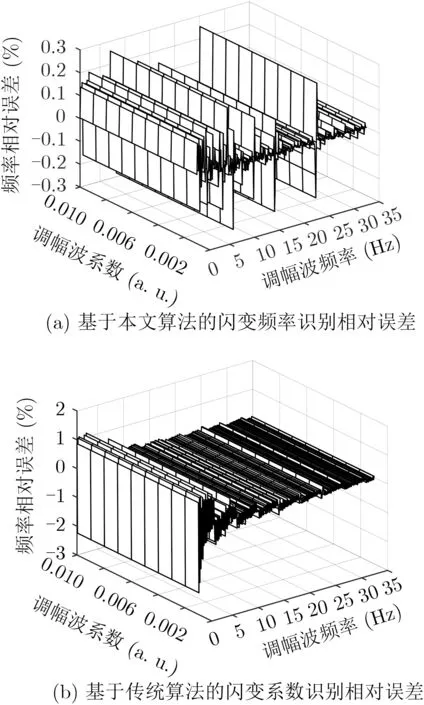
图5 单频调制分量时的闪变频率识别误差
5.2 多频率包络调制
为验证本文算法在多频率调制波下的闪变参数识别的精准性,仿真设置的多频率矩形波包络调制电压闪变信号参数如表1所示,以2阶莱芙-文森特自卷积窗(Rife-Vincent Self-Convolution Window,RV-SCW)三谱线校正识别法作为对照组,其余参数设定值固定,仿真结果如图6、图7所示。

表1 多频率包络调制仿真参数设置
由图6、图7的ekl和efl分布图可得,基于本文算法得到的kl与fl测量精度在10E-2%数量级与10E-3%数量级左右,与单频率包络调制的识别误差增值不大。本文算法针对第1组分量的ml,fl检测误差为1.2E-2%,–8.1E-3%,且相比于对照组算法分别提高了2个及1个数量级。

图6 多频调制分量时的闪变系数测量误差分布图
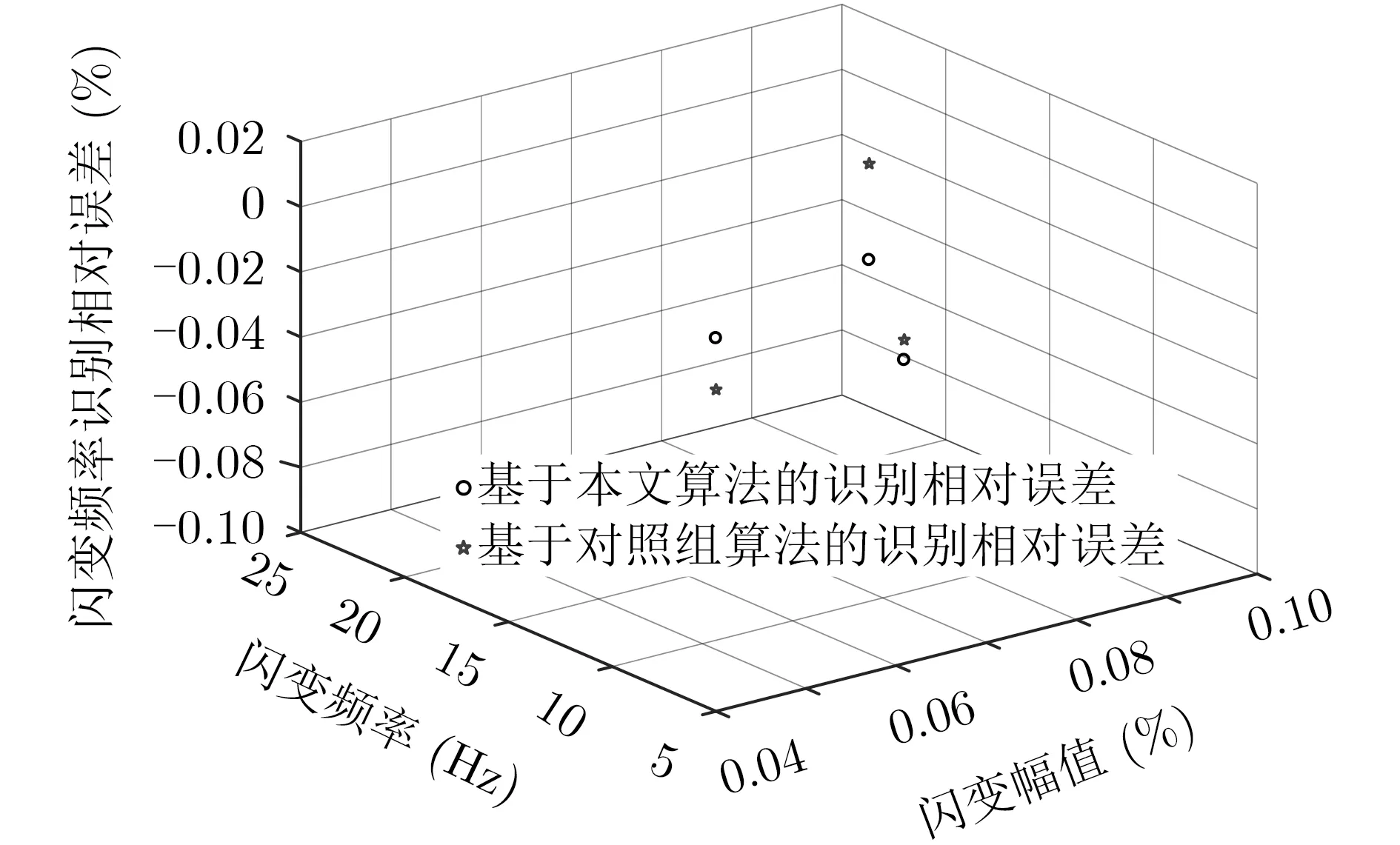
图7 多频调制分量时的闪变频率测量误差分布图
5.3 次/超同步谐波对闪变参数识别精度的影响
新能源以及电力电子设备技术表现性能优越,但也会给电网注入次/超同步频率分量,可能降低系统包络参数识别准确度。对矩形波调制闪变信号叠加不同类型的次/超同步谐波分量,并使其频点值不断接近,具体参数设置为:(1)含有20 Hz与80 Hz间谐波分量;(2)含有20 Hz与55 Hz间谐波分量;(3)含有25 Hz与35 Hz间谐波分量;幅值均设定为0.5%,检测相对误差分布如图8所示。
由图8可知,当闪变信号中存在次/超同步间谐波分量时,参数识别精度相比于无谐波与稳态谐波均有所下降,闪变幅值为10E-1%~10E-3%数量级,闪变频率为10E-1%~10E-3%数量级。当次谐波的频率不断靠近闪变频率误差峰值点25 Hz时,估计误差值也达到最大,幅值相对误差为3%,频率相对误差为2.57E-2%。另外,当谐波频点值不断接近时,闪变参数检测相对误差增值也随之增大,但仍能满足整体检测要求且比传统能量算子法的准确性高。
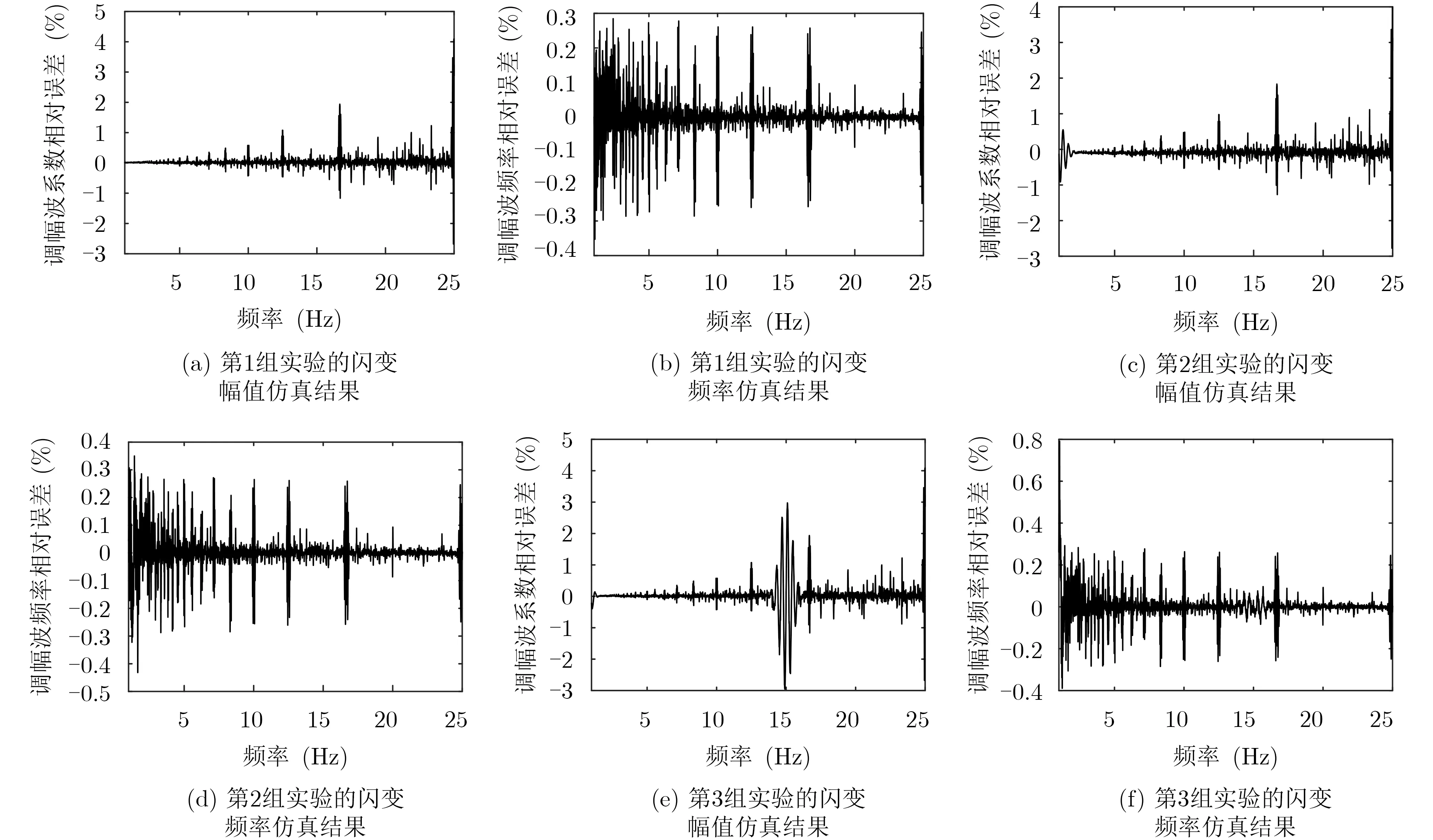
图8 叠加次/超同步谐波的参数估计误差分布
5.4 电网基频变动影响
电网实际频率值不是固定不变的,而受负荷变化的影响在50 Hz附近发生偏离,会不同程度影响闪变参数检测结果。为验证识别方法在基频波动下的有效性,设置基频变动处于(49.5 Hz,50.5 Hz)范围内,闪变频率区间为:(1 Hz,35 Hz),调幅波电压的幅值0.1 a.u.,其他参数设置固定,得到结果如图9所示。
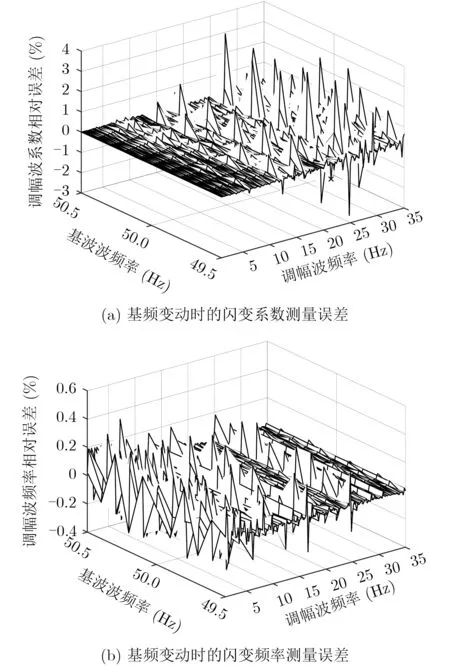
图9 基频变动时的参数测量误差
由图9可知,当基频存在偏移现象时,本文闪变系数和频率参数的识别误差分别为(10E-1%,10E-3%)数量级和(10E-3%,10E-5%)数量级,参数估计误差基本与信号频率不变动时保持在同一个数量级。可见,本文算法能够有效克服频率变动时闪变参数估计精度降低的问题。
5.5 添加噪声干扰影响
风电并网运维环境中不可避免地存有噪声干扰,严重影响对参数分析准确度。在前面仿真实验基础上添加不同信噪比(Signal-Noise Ratio,SNR)的噪声源,改进优化算法的ekl和efl分布如图10所示。
由图10可知,在添加白噪声之后,闪变参数测量误差相较于实验室环境有所增大。对于不同的闪变调制频率,当信噪比较小时(SNR ≤35 d B),闪变包络的参数提取误差较大,如SNR=23 d B时,kl相对误差约为1%数量级,fl相对误差约为10E-3%数量级;随着SNR值的增加(SNR>35 dB),闪变包络各分量参数识别精度也逐渐提高。仿真表明,算法在噪声背景下仍可实现预期识别功能。
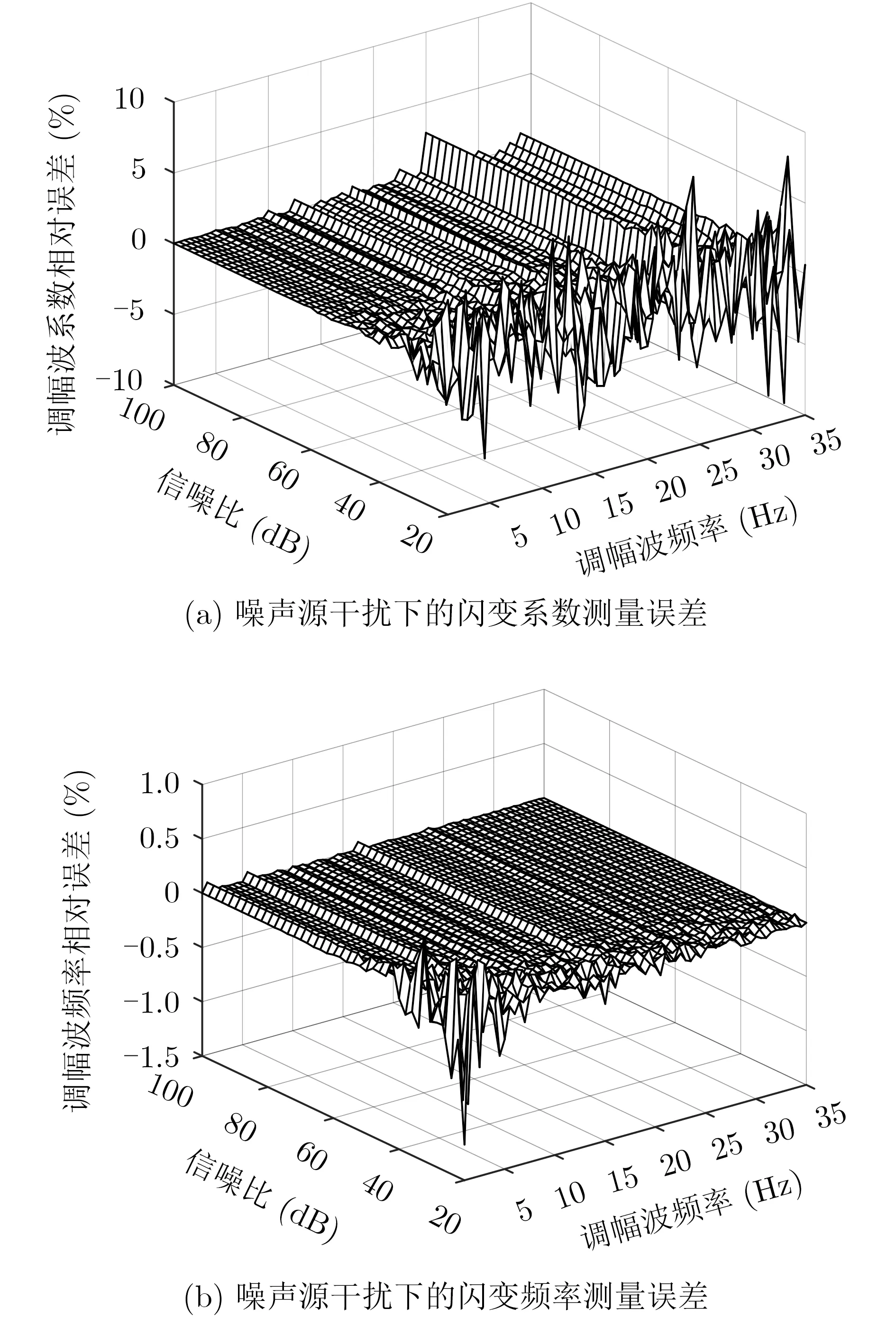
图10 噪声源干扰下的参数测量结果
5.6 不同采样点数影响
信号采样长度对加窗插值进行闪变参数识别有直接的影响,设MSLD-SCW函数长为1024点、2048点、4096点及8192点对矩形波调制闪变信号进行加权,闪变系数及频率提取误差如图11所示。
由图11可知,采样点数在2048时,电压闪变系数和频率识别误差为-0.8.612E-1%及-1.7E-2%,已能满足IEC检测要求。随着N的增加,测量精度增值并不明显但分析时延特性明显下降。因此,选择合适点数可以得到较高的计算精度,还能减少计算量和分析延迟。
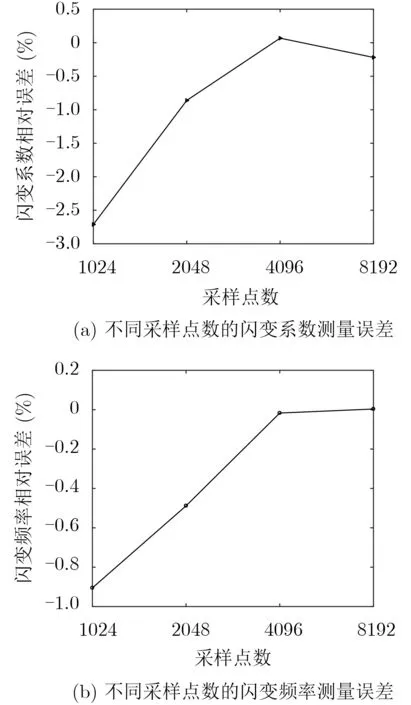
图11 不同采样点数的参数识别结果
6 实际应用与讨论
目前包括新疆在内的风资源分布广泛地区的风电场群规模不断增大,风电并网接入技术不断完善提高。与此同时,包括闪变等在内的电能质量问题也越来越严重[16]。将本文算法运用到新疆哈密地区实际电网电压闪变参数检测中,以证明算法能够有效且高准确性地实现检测功能。图12(a)—图12(c)为从现场采集到哈密麻黄沟地区线路1,2的A相电压录波值及麻黄沟龙源风电场某1.5 MW风机出口线路1的A相电压实时录波值,从3条线路录波图可看出,电压波动性明显且波形畸变严重。通过分析系统上位机软件实现对离散化后的数据进行分析与处理,实现电压闪变包络参数识别功能。
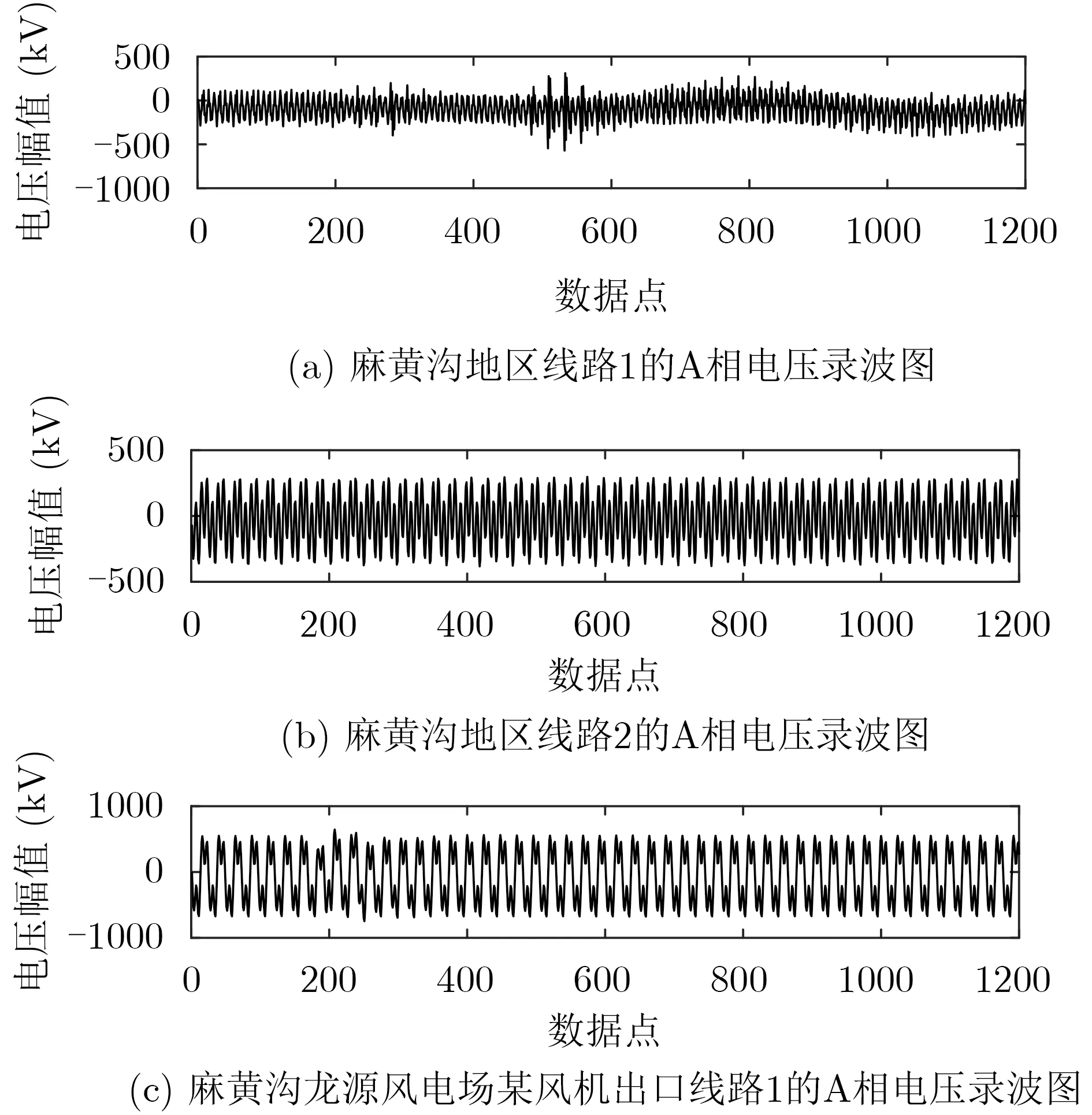
图12 3条线路实测电压波形
分别选用传统能量算子算法与改进能量算子和6项余弦截断窗频谱校正的识别法作为对照组,得到图13—图15所示的闪变包络参数分析结果。从图13—图15可得,线路电压存在微弱闪变,且基于本文提出算法的电压闪变参数准确性较高。如对于麻黄沟线路2,基于对照组算法的第1闪变包络分量的闪变系数识别误差相对于本算法为0.0025;频率检测相对误差为0.0761。又如,对于麻黄沟龙源风电场出线,基于传统能量算子的第1闪变包络分量的闪变系数识别相对误差对比于本算法为22.772%,泄露量较大;频率检测相对误差为2.703%。通过上述分析可以得出,本文算法能够更精准、有效地实现电网电压闪变参数识别与分析。
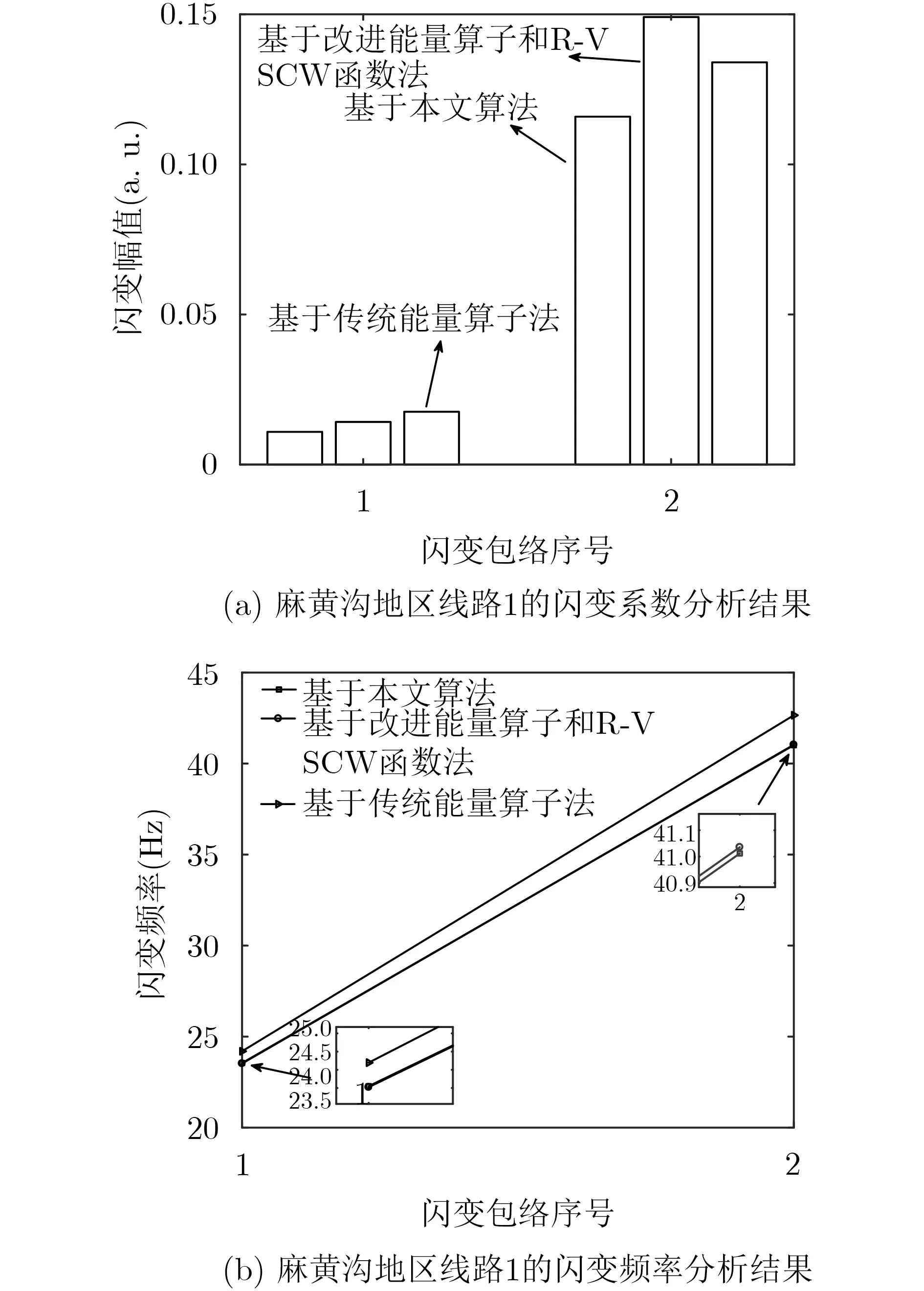
图13 麻黄沟地区线路1的参数测量结果
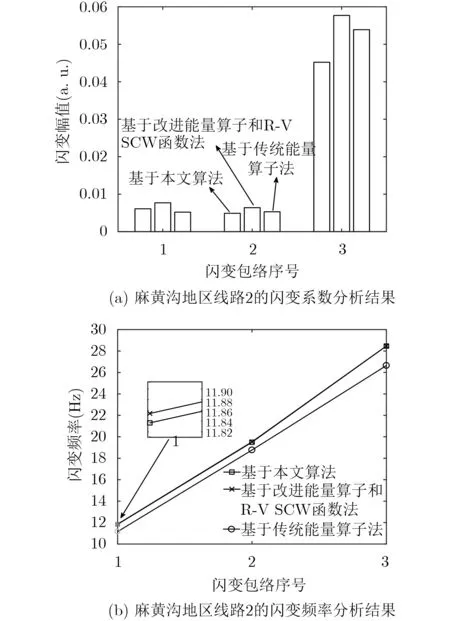
图14 麻黄沟地区线路2的参数测量结果
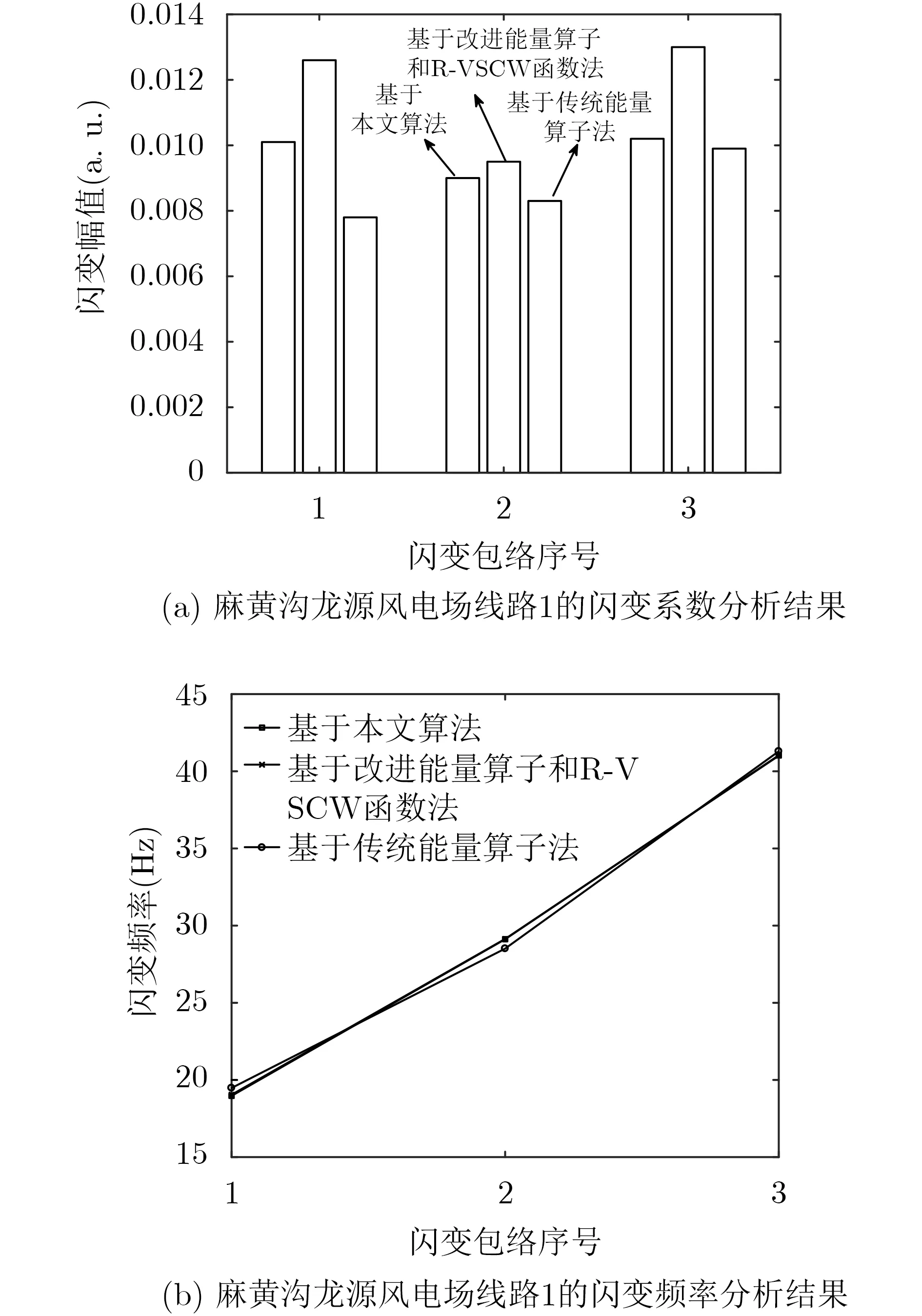
图15 麻黄沟龙源风电场线路1的参数分析结果
7 结论
针对矩形波调制电压闪变模型,本文提出基于优化改进算子和新型MSLD-SCW函数谱线校正FFT的闪变参数识别方法。与传统能量算子相比,通过优化采样间隔,使得包络提取精度高且追踪幅值与频率参数的性能更优。另外,通过改进的加卷积截断窗谱线校正FFT算法,可以更好地克服谱间泄露与栅栏效应对参数识别精度的影响。经仿真实验验证:本文所提的电压闪变参数识别法的检测准确性受电网基频变动、谐波/间谐波、次/超同步谐波分量、白噪声的干扰较小,且均可有效实现参数的准确提取。最后,将所提算法应用于新疆某地区实际电网闪变识别中,证明其能够满足复杂电网运行工况背景下的闪变包络参数识别与分析的需求。
