声学超表面的非对称声分束特性研究
2021-08-26宋爱玲孙超彧陈天宁项延训轩福贞
宋爱玲,孙超彧,陈天宁,项延训,轩福贞
(1.华东理工大学机械与动力工程学院,上海 200237;2.西安交通大学机械工程学院,西安 710049)
0 引 言
声学超材料[1]是类比电磁学超材料提出的一种具备特殊物理性能的新型复合材料,在国防安全、工业发展和社会环境等领域有巨大的应用前景,近年来成为声学领域的前沿研究热点。自然界中各种形式的能量传播都遵循互易原理,声波作为一种经典波其传播同样也遵循互易原理[2-3]。声学领域中没有与其他领域类似的单向机制,且存在线性条件下互易原理的限制,致使实现非互易声传播存在着很大的理论和技术困难。实现非互易声传播均需要打破系统的时间反演对称性,可以采用流动介质、非线性材料、时空调制结构参数等方法实现。另一种实现声波单向传播的方法是破坏结构的空间反演对称性,近十年来,国内外学者利用声子晶体、声学梯度材料、声学超表面、声学栅等声人工材料设计线性非对称声学系统打破空间反演对称性实现了非对称声传播,在能量传输效率、工作带宽和结构尺寸等方面均具有很大的天然优势。
在一些特殊场合人们希望声波可以沿两个甚至多个方向进行传播,例如声通信中希望将声信号传递给不同方向的接收方,且可以任意控制接收方收到的信息量。声通信作为一种收发信息的技术,在国防军事领域发挥着重要作用。声分束器[4]是将一束波分成两束或多数波的装置,为声通信技术的发展提供了一种参考方法。但目前关于声波分束尤其是非对称分束的研究尚少,因此探索新型的声波分束方法具有重要的理论和实际意义。不同于声子晶体[5-6]和零折射率材料[7-8]实现声波分束,超结构由于其独特的波场调控特性可以对反射波或透射波进行有效分束操控。在电磁学领域,许多学者开展了电磁波分束的研究[9-11],但多局限于较简单的对称分束情况,关于非对称分束的研究均围绕反射波展开[12-13]。近年来,对声波分束的研究受到人们的广泛关注[14-17],但与电磁波分束类似,对声波非对称分束的研究也主要集中在对反射波的调控[18-19],声学领域中对透射波进行非对称分束的研究尚少,严重限制了其在许多领域的实际应用。根据声分束器两束透射波的折射角和分束比,非对称声分束可以分为三种类型:相同折射角分束比非1,不同折射角分束比为1,以及不同折射角分束比非1,这三种非对称声分束器的阻抗矩阵分布、法向声强分布及子单元几何参数均会呈现出不同的特点,且在不同的应用场合中有应用前景。Li等[20]仅从理论上研究了一种不同折射角分束比非1的非对称声分束器,因此进一步系统研究其余类型的非对称声分束器对于丰富声波分束的物理特性,实现其在声功能器件和声通信中的应用具有重要的理论指导意义。
本文针对透射波非对称分束传播的实际应用需求,基于局域声功率守恒条件[20]研究了一种实现非对称声分束的设计理论和实现方法。首先,对声分束器入射侧和透射侧的局域声功率分布进行分析,探讨实现局域声功率守恒的方法,并获得声分束器所需的阻抗矩阵分布;其次,对四串联共振腔结构进行几何参数优化,利用互易的双各向异性结构实现所需的阻抗矩阵分布;最后,运用有限元数值方法对声压场分布进行计算,对声波分束效果进行有效性评价。本文的研究工作可以为非对称声分束结构设计提供一种参考思路,并促进其在工程领域的实际应用。
1 非对称声分束模型及局域声功率分布
1.1 非对称声分束理论模型
本文提出一种透射型声波分束超表面,其工作原理示意图如图1(a)所示。声波分束器沿y轴方向竖直放置,可将左侧垂直入射的声波分成两束沿任意方向传播的透射波,且可以指定两束透射波的分束比。两束透射波的折射角分别为θ1、θ2,透射系数分别为T1、T2,且T1=t1ejφ1,T2=t2ejφ2,t1和t2为透射系数幅值,φ1和φ2可以反映透射系数的相位情况。

图1 非对称声分束效果示意图
1.2 局域声功率不匹配
首先分析声分束器两侧的声压、质点速度及声强分布。对于左侧入射的声波,入射波的声压和质点速度可以分别表示为:
pi=p0e-jk0x
(1)
vi=p0e-jk0x/Z0
(2)
式中:p0为声压幅值;k0为声波在空气中的波数;Z0为空气的声阻抗。根据声分束器入射侧表面x=0处的声压pi(x=0)=p0和质点速度vi(x=0)=p0/Z0,可得声分束器的入射声强为:
(3)
由于声分束器将入射波分为两束波,因此透射区域的声场为两束透射波之和,透射波的声压和法向质点速度分别表示为:
pt=T1p0e-jk0 cos θ1 xe-jk0 sin θ1 y+T2p0e-jk0 cos θ2 xejk0 sin θ2 y
(4)
(5)
在声分束器透射侧的表面,即x=0处的透射波声压和法向质点速度分别为:
pt(x=0)=T1p0e-jk0 sin θ1 y+T2p0ejk0 sin θ2 y
(6)
vtx(x=0)=T1p0cosθ1e-jk0 sin θ1 y/Z0+T2p0cosθ2ejk0 sin θ2 y/Z0
(7)

(8)
由公式(8)可发现,法向透射声强是与折射角和透射系数相关的余弦函数,在非对称声分束情况下均呈现周期性分布。由于结构具有周期性且希望沿声分束器法线方向的入射声功率能够全部传递到透射侧,因此根据声分束器法线方向的总声功率守恒条件可得:
(9)
(10)
可以发现t1,t2均与折射角θ1,θ2及分束比m相关,表明当折射角和分束比确定后,两束透射波的透射系数也可唯一确定。根据声传输线理论,声分束器两侧的声压和法向质点速度可通过阻抗矩阵建立联系:
(11)
令上式中的实部和虚部分别相等,可得到定义该声分束器的阻抗矩阵分布。当声学系统内部无损耗时,阻抗矩阵的所有元素均为纯虚数,归一化阻抗矩阵的元素虚部为Xij=Im(Zij)/Z0。下面讨论一种最简单的声波分束情况,即对称分束:两束透射波折射角相等(θ1=θ2=θ)且分束比为1。由公式(11)可得Xij分别为:
(12)
下面对sinθ1=sinθ2=0.6的对称声分束器进行分析,频率为3 000 Hz时,声分束器一个周期中的阻抗矩阵分布情况如图2(a)所示,D为声分束器周期长度。此时X12≠X21,表明系统中需引入非互易性才可实现声波分束功能,存在很大的实现难度。对于任何线性时不变系统而言,其互易性条件要求X12与X21相等。

图2 对称声分束器的归一化阻抗矩阵分布(a)和归一化法向声强分布(b)
另一方面,对声分束器入射侧和透射侧的法向声强分布进行分析,结果如图2(b)所示。可以发现入射侧平面波的声强沿y轴方向呈均匀分布,而透射侧的声强表现出余弦形式的波动,声强变化周期为D/2。由于透射侧两束声波互相干涉,导致透射声能量呈现非均匀性,该现象表明声分束器的某些区域需要从外界吸收声能量,而其余区域需要向外界发射声能量。本文将入射波和透射波的法向声强沿声分束器不同位置的分布情况称为“局域声功率”,可以看到声分束器两侧的局域声功率存在不匹配问题,结构的不同区域间需要互相传递声能量,在实际设计和实现中具有很大的难度。
1.3 局域声功率守恒条件
由前述分析可知,通过声分束器两侧声压及质点速度求解阻抗矩阵的方法存在局域声功率不匹配问题,导致设计实现中存在很大难度。为了匹配入射侧和透射侧的声功率,假定在声分束器的入射侧激发出两列传播方向相反的表面波[20],如图1(b)中的黑色弯曲箭头所示。需要说明的是,这两列表面波是声波入射到声分束器上后自主激发产生的。下面根据声功率守恒条件,确定这两列激发表面波的参数,再次对声分束器进行设计。当入射侧存在激发表面波时,入射侧的声场为入射波及两列表面波之和,入射侧声压为:
p1=p0e-jk0x+a1sp0eα1xe-jk1y+a2sp0eα2xejk2y
(13)

出于一般性考虑,在表面波1和表面波2中分别引入ejβ1和ejβ2的相位变化,则公式(13)变为:
p1=p0e-jk0x+a1sp0eα1xej(-k1y+β1)+a2sp0eα2xej(k2y+β2)
(14)
同样可以得到入射侧的法向质点速度为:
(15)
在声分束器入射侧的表面,即x=0处的声压和法向质点速度分别为:
p1(x=0)=p0+a1sp0ej(-k1y+β1)+a2sp0ej(k2y+β2)
(16)
(17)

(18)
为了满足局域声功率守恒条件,公式(18)中的入射侧声强I1x(x=0)应与公式(8)中的透射侧声强Itx(x=0)相等。Itx(x=0)中仅含有关于变量y的余弦函数,而I1x(x=0)中同时含有关于变量y的正弦函数和余弦函数,令a1s=a2s=as,α1=α2=α。同时为了合并I1x(x=0)中剩余的两项余弦函数,令β1=β1=0,则I1x(x=0)简化为如下形式:
(19)
此时可以求得方程I1x(x=0)=Itx(x=0)的解为:
as=0.5t1t2(cosθ1+cosθ2)
(20)
(21)
至此确定了声分束器入射侧两列激发表面波的相关参数,需要说明的是公式(20)和(21)只是方程I1x(x=0)=Itx(x=0)的其中一个解,但该解具有最简单的形式。分析公式(20)和(21)中表面波的参数可以发现,对于所有的声波分束情况,入射侧始终存在传播方向相反,且幅值和衰减系数均相同的在两列表面波,其与入射波相互作用后使入射侧与透射侧的局域声功率互相匹配,且该方法具有很好的普适性。
当入射侧存在激发表面波时,声分束器两侧的声压和法向质点速度仍可通过阻抗矩阵建立如下联系:
(22)
下面再次分析sinθ1=sinθ2=0.6的对称声分束器,一个周期中归一化阻抗矩阵的分布情况如图3(a)所示,可发现声分束器满足局域声功率守恒条件时X12=X21,表明此时声分束器满足互易性条件,可以通过设计简单的被动声学系统实现。其次,可以注意到X11与X22不相等,说明该声分束器的单元结构具有双各向异性特性。另外,归一化阻抗矩阵的四个元素在一个周期中的分布均关于声分束器的周期中心对称,这是由于研究的是完全对称的声分束情况,因而声分束器的声学特性也具有对称性。

图3 入射侧激发表面波时对称声分束器的归一化阻抗矩阵分布(a)和归一化法向声强分布(b)
同样,再次分析声分束器入射侧和透射侧的法向声强分布,如图3(b)所示。可以看到声分束器入射侧和透射侧的声强具有很好的匹配性,均表现出周期为D/2的余弦形式波动。当入射声波激发出两列表面波后,入射侧的声强不再呈均匀分布,这三列声波相互干涉后的法向声强分布与透射侧声强刚好匹配,从而满足了局域声功率守恒条件。通过声波对称分束的研究发现,声波入射到声分束器后激发出两列表面波,为实现局域声功率守恒提供了可能,并且该方法在理论上具有很好的普适性,适用于非对称声分束器设计。
2 非对称声分束器设计
对两束透射波沿不对称方向传播、分束比为1的非对称声分束情况进行研究,为了更好地与文献[20]中的结果进行比较,同样选取两束透射波的折射角分别为θ1=36.87°,θ2=64.16°,此时sinθ1=0.6,sinθ2=0.9,下面对这种不同折射角1∶1分束比的声分束器进行设计。根据总声功率守恒条件可得两束透射波的透射系数均为t1=t1=0.90,传播到θ1和θ2方向的法向声能量比例分别为I1=64.73%,I2=35.27%,另规定φ1=φ2=3π/4。在这种声波分束情况下,可得到声分束器的周期为D=2π/(3k0/10)=381.1 mm,其与文献[20]中不同折射角2∶1分束比情况下的周期相同,说明声分束器的周期仅由两束透射波的折射角决定,与分束比无关。根据局域声功率守恒实现方法,入射侧激发的表面波幅值系数为as=0.50,衰减系数为α=1.118k0,对比文献[20]的结果可以发现表面波的衰减系数仅由两束透射波的折射角决定,也就是在两束透射波的折射角确定的情况下,改变分束比不会对表面波的衰减系数产生影响,但会影响其幅值系数。声分束器的归一化阻抗矩阵分布情况如图4(a)所示,X12=X21且X11≠X22说明该结构是双各向异性的互易系统。声分束器入射侧和透射侧的法向声强分布如图4(b)所示,可以看到入射侧与透射侧的法向声强可以很好地吻合,且在声分束器的一个周期中呈周期性分布,周期为D/5,其与不同折射角2∶1分束比情况中的周期相同,表明声分束器的法向能量变化周期仅由两束透射波的折射角决定,与分束比无关,但分束比会影响法向声强的极值大小。

图4 不同折射角1∶1分束比时声分束器的归一化阻抗矩阵分布(a)和归一化法向声强分布(b)
声分束器的一个周期离散为28个子单元,每个子单元的宽度为w=D/28=13.61 mm,采用图5所示的四串联共振腔结构[21-22]并利用遗传算法进行参数优化以实现所需的阻抗矩阵分布。每个子单元由四个串联排布的亥姆霍兹共振腔组成,且相邻子单元之间形成矩形直管。改变共振腔结构的任何几何参数均会对其阻抗矩阵产生影响,但改变5个宽度参数w0、w1、w2、w3、w4对阻抗矩阵产生的影响最为明显,因此本研究仅对这5个宽度参数进行优化,而其余的几何参数保持定值。四串联共振腔结构的几何参数包括:子单元宽度为w=12.7 mm,壁厚为t0=1 mm,短管长度为s=1.5 mm,四个空腔的长度为l=12.25 mm,矩形直管的宽度为w0,四个空腔的宽度分别为w1、w2、w3、w4且均不相同以满足双各向异性结构对形状非对称的要求,四串联共振腔结构的几何参数除w0、w1、w2、w3、w4外均为定值。利用矩形直管Fabry-Pérot共振与四个共振腔共振之间的耦合,可以通过同时调节矩形直管宽度w0和四个空腔宽度w1、w2、w3、w4对子单元结构的阻抗矩阵进行调节,下面对四串联共振腔结构的阻抗矩阵表达式进行求解。

图5 四串联共振腔结构示意图
首先建立结构的传递矩阵,对其进行转换后可以求得对应的阻抗矩阵。根据声传输线理论,声分束器两侧的声压和法向质点速度可以通过传递矩阵[T]建立如下联系:
(23)
当用四串联共振腔对声分束器进行设计时,每个子单元的总传递矩阵[T]可用多个传递矩阵乘积表示:
[T]=[Tin][M0][T1][N0][T2][N0][T3][N0][T4][M0][Tout]
(24)
根据传递矩阵和阻抗矩阵之间的转换关系,可以得到四串联共振腔结构的阻抗矩阵[Z]为:
(25)
由以上分析可知,阻抗矩阵的四个元素均与亥姆霍兹共振腔的几何参数相关,因此调节矩形直管宽度w0和四个空腔宽度w1,w2,w3,w4可以改变子单元结构的阻抗矩阵并实现目标离散阻抗矩阵值。采用遗传算法对5个参数进行全局优化搜索,对每个子单元进行60次优化以找到最佳参数值。优化过程的搜索收敛性用目标函数cost函数表示,其表示参数优化后结构的阻抗矩阵值与理论阻抗矩阵值间的差异:
(26)
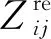
运用上述遗传算法对每个子单元的5个几何参数进行优化搜索,使其可以实现目标离散阻抗矩阵值,表1为不同折射角1∶1分束比时的子单元几何参数。本文所设计非对称声分束器的cost函数最大值约为100,但文献[20]中cost函数的最大值高达352.22,表明两束透射波的分束比非1时存在某个子单元的设计误差非常大,子单元阻抗矩阵的实际值与理论值之间存在巨大的差异。另一方面,可以计算各个波数分量对应的法向声强值分布,其反映了声能量沿声分束器法线方向的分配情况。波数分量ky对应的法向声强Ix(ky)可以表示为:

表1 非对称声分束器的子单元几何参数
(27)
式中:p(ky)为波数分量ky对应的声压幅值。
3 结果与讨论
为了直观地观察非对称声分束器的分束效果,一束高斯波束从左侧垂直入射到声分束器上,其声波传播情况如图6所示。可以看到声分束器将入射的高斯波束分为两束波,两束波沿不同的传播方向进行传播,并且两个透射波束的声压幅值基本相同。此外,可以在入射侧靠近声分束器的区域清晰地观察到激发表面波的存在。因此,该声分束器很好地实现了不同折射角1∶1分束比的分束效果。
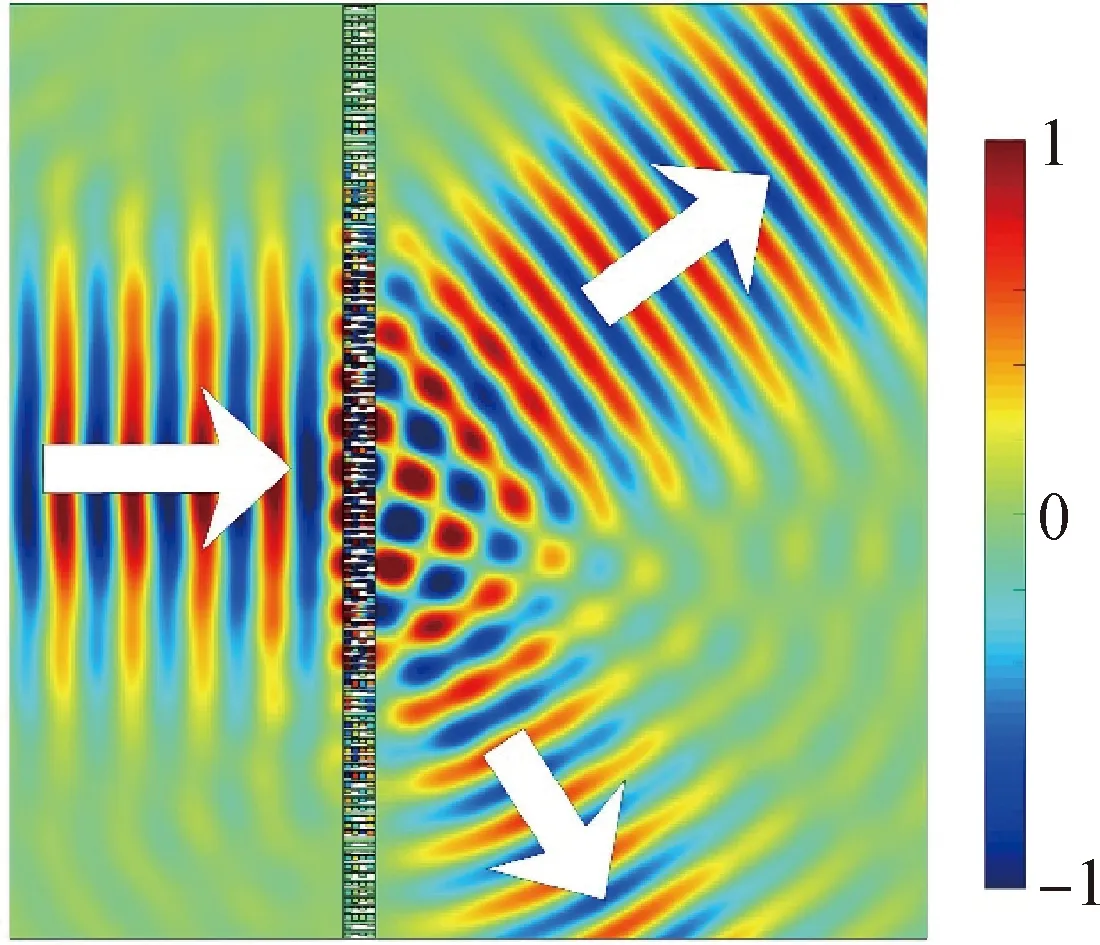
图6 不同折射角1∶1分束比声分束器的分束效果
下面对该声分束器的分束效果进行量化分析,各个波数分量对应的声压幅值如图7(a)所示。可以看到声分束器的透射侧主要存在两束透射波,两束波的折射角不同,分别为sin-1(0.6)=36.87°(理论值θ1=36.87°),sin-1(0.9)=64.16°(理论值θ1=64.16°),声分束器实现的折射角与理论值完全一致,其余波数分量下的声压幅值均比较小。另外,上方波束的透射系数为0.907 7(理论值t1=0.90),下方波束的透射系数为0.874 4(理论值t2=0.90),分束比为1.07(理论值m=1)。此外,各个波数分量对应的法向声强值分布如图7(b)所示,可以看到上方波束的法向声能量为65.92%(理论值I1=64.73%),下方波束的法向声能量为33.33%(理论值I2=35.27%),透射侧中仅有0.75%的声能量传播到其余方向。由以上分析可以看出,该声分束器较好地实现了设计目标,但也存在的问题是上方波束的声能量比理论值偏大,下方波束的声能量比理论值偏小,偏差可能是由声阻抗矩阵实现误差及子单元离散度引起的。
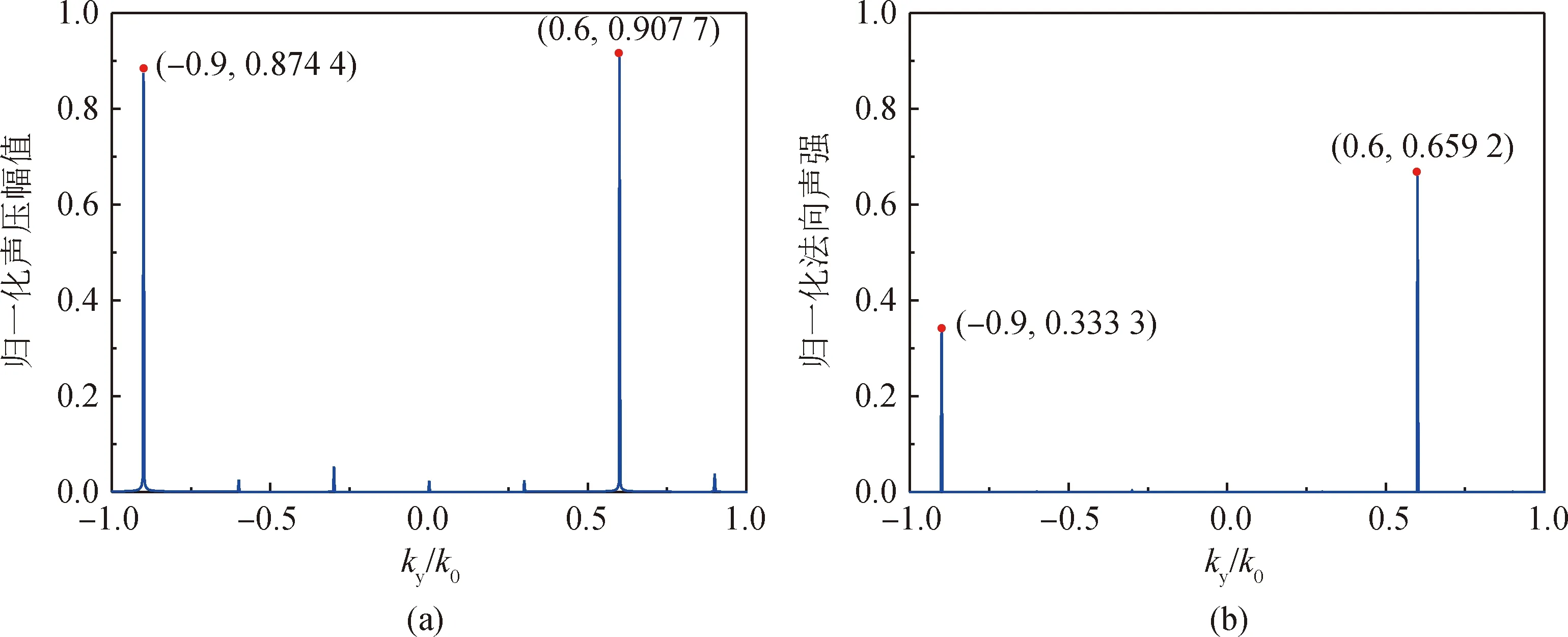
图7 不同折射角1∶1分束比时声分束器的归一化声压幅值(a)和归一化法向声强(b)
4 结 论
本文基于局域声功率守恒条件系统研究了一种实现非对称声分束的设计理论,并开展了系统的理论分析、结构设计和数值模拟验证,研究了声分束器的阻抗矩阵分布、法向声强分布、声压场分布等,并通过分析透射侧的声压幅值和法向声强对声波分束效果进行有效性评价。对声分束器入射侧和透射侧的局域声功率分布分析表明,在入射侧激发两列传播方向相反且幅值和衰减系数均相同的表面波,其与入射波相互作用后可以实现入射侧与透射侧局域声功率的相互匹配。这种基于局域声功率守恒的设计方法具有广泛的普适性,可以通过设计互易的双各向异性结构实现非对称声分束功能。采用遗传算法对四串联共振腔结构进行参数优化,并利用双各向异性结构可以实现所需的阻抗矩阵分布。对声分束器透射侧的各个波数分量对应的声压幅值和法向声强进行分析发现,入射声波经过声分束器后被分为两束波,两束波的折射角和透射系数与理论值十分吻合,很好地实现了预期的声波分束效果,证明了该设计理论在实现声波非对称分束时的正确性和可行性。
本文的研究工作表明利用四串联共振腔设计的互易双各向异性结构可以有效实现非对称声分束功能,基于局域声功率守恒的实现方法具有理论正确性和实际可行性,丰富了声学领域中声波分束的相关研究,该实现方法为获得非对称声分束结构提供了一种参考思路,并为进一步探索声波分束在声功能器件设计和声通信中的应用奠定了理论基础。
