随机等价在多层异构无线网络中的分析

孙玉红,王家涛,韩丽娟

(①曲阜师范大学计算机学院;②山东水利职业学院建筑工程系;③曲阜师范大学实验与设备中心,276826，山东省日照市)

随着对覆盖率和数据传输速率要求的提高，多层异构网络受到了广泛的关注，逐渐成为未来无线通信的一种解决方案.多层异构网络由具有不同发射功率和覆盖范围的节点组成.以蜂窝网为例，不同的节点(例如，传统的宏小区网络及小小区网络)各自构成一个网络层，每一单层的(即同构的)蜂窝网络可以作为一个独立的情况来看待.因此多层异构网络可以看作是对现有网络结构的扩展.近年来，这种异构化随着业务需求而迅猛增长.

对异构蜂窝网络的研究，迄今为止，大部分的分析方法是通过仿真.以前的方法使用基站分布为六边形网格的模型，该模型用来模拟真实世界的基站部署时，与实际情况相差较大.因为地理条件，如山、湖、河流、街道等原因，很少允许基站按照规则的六边形部署，而且大部分的仿真是运行在模拟器上的，结果之间很难验证和比较.因此，该方法难以得到主要的系统性能指标如覆盖率和用户以及基站密度的关系.这些关系在一些优化问题中，比如能量消耗，部署成本等问题中有重要意义[6].随着技术的发展，随机几何再次成为一个有利的工具用于分析异构无线网络的性能.本文利用随机几何，研究了将多层独立的泊松网络等价为单层均匀网络的方法，基于此等价，多层网络可以转化为易处理的单层模型.

1 相关研究

随机几何是一个非常有用的数学工具和统计工具，用于无线网络的拓扑随机性的建模、分析和设计[1-6].它在Ad hoc网络分析中已有30多年历史,特别是用于随机信道访问的网络分析，如Aloha网络或 CSMA网络以及单层和多层的蜂窝网络的分析[7,10].

在无线网络的研究中，有多种空间点过程的模型用于网络的建模和性能分析，如泊松点过程(PPP)[5]，泊松簇过程(PCP)[6]，硬核过程(MHC)[8]，软核过程(Strass)[10],行列式点过程(DPP)[9]等.在这些点过程中，以泊松点过程(PPP)的使用最为广泛，因为该点过程既可以模拟实际的基站分布的随机性，又有易分析的性质，从而容易分析出网络的性能.相比较传统的六边形网格表示的基站分布，无论在准确性还是实用性上都具有极大的优势.对节点分布为PPP的单层网络的性能分析和研究已有了大量的成果[5].

对于节点分布为PPP的多层异构网络的研究，文献[1]研究了各层分布为不同密度的独立PPP的网络覆盖率和数据传输速率.文献[15]研究了在多层异构网络中使用串行干扰消除(SIC)的网络性能.文献[6]分析了多层蜂窝网的网络性能，其中宏基站用PPP建模，小基站用PCP进行建模.由于宏基站分布的排他性，相邻的两个宏基站不可能距离很近，与PPP中点的分布无关性并不完全一致，因此一些非PPP的建模方法也用于研究蜂窝网，例如文献[11]研究了用Ginibre点过程(GPP)模型来模拟宏基站的方法，并对网络性能进行了分析.

对一般的点过程(非PPP)，文献[12]提出了非PPP点过程在计算覆盖率的时候，与PPP具有相同的变化趋势，因此可以用平移的PPP来近似其性能，并认为这是一种增益，称为渐近部署增益(ADG).文献[13]进一步确定了在瑞利衰落条件下，平均干扰信号比(MISR)的重要作用，即增益的计算方式.此近似方法即基于PPP的近似信干比(SIR)分析(ASAPPP)[14].由于一般的稳定点过程可以通过ASAPPP方法进行ADG平移，进而转化为PPP网络，因此本文主要研究基于PPP分布的网络结构.

多层网络由于多样性，相比较单层网络的分析困难得多，因此如何将已有的对单层网络的研究成果运用到多层网络中是一个非常有意义的问题.本文根据该问题，主要从网络随机等价的角度研究将多层网络等价为一层网络的方法.网络等价分别从传输功率和分布密度两个角度将多层网络等价为单层网络，从而得到多层网络的易于处理的方法.

2 网络模型

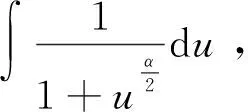
3 网络等价

本部分根据各层网络节点分布为独立的PPP的情况下，从两个角度给出网络随机等价的处理.网络等价的意义是在干扰总量不变的情况下，对网络的一些参数进行统一处理，通过等价处理，一些在单层网络中的分析方法能直接推广到多层网络中.

3.1 功率等价

在各层节点分布为PPP的情况下，假设典型用户由第k层服务节点xs提供服务，其所受到的干扰来自于本层的其他节点，和其他层的所有节点.由于异构网络的特点，各层节点的发送功率不同，根据用户所接收到的累积干扰，假设用户位于一个单层网络中，在累积干扰等价的条件下计算其等价功率.

在多层网络中，假设用户与第k层节点相关联，对用户产生干扰的基站为xj，用户所接受到的累积干扰可以表示为

前一项Ii≠k表示来自其他层的干扰，后一项Ik表示来自第k层的干扰.

首先计算LIk(s)：

(a)

(b)

因此，所有干扰层的Laplace变换可以写为

令LIT(s)=LIT′(s)，可得，

(1)

因此，网络可以在保持典型用户所接受的服务信号的功率和累积干扰都不变的条件下，等价为一个发送功率为Peq，节点密度为λT的单层网络.

3.2 密度等价

在干扰总量等价的条件下，如果以某一层网络的功率为标准功率，可以计算多层网络的等价密度，从而也能将多层网络等价为单层网络.

类似地，对与第k层节点关联的用户，其所受到的干扰来自于k层的其他节点，和其他层的所有节点.与功率等价的推导类似，在多层网络模型中，用户所受干扰的Laplace泛函为

另一方面，假设网络是一个密度为λeq，节点发送功率为Pk的单层网络Φeq，典型用户所受的干扰总量的Laplace泛函为

因此，令LIeqc(s)=LIT(s)，得到等价密度为

(2)

所以，多层网络也可以在保持典型用户所接受的服务信号的功率不变，和累积干扰功率不变的条件下，等价为一个发送功率为Pk，节点密度为λeq的单层网络.

3.3 分析

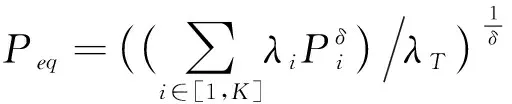
命题1 对于任意层k∈[1，K]，在开放访问的模式下，以上2种网络等价不影响用户的覆盖率(成功传输概率).

证明首先，在多层网络中，对第k层的用户，其覆盖率可以表示为

因此第1种网络等价不影响第k层用户的覆盖率.

同理，在第2种网络等价模式中，等价密度λeq为用户的干扰密度，而当限定为第k层节点关联的用户时，其服务密度为λk，因此，

与式Pc_k一致.命题得证.

命题2 两种随机等价在开放访问的模式下不影响网络整体的覆盖率.

证明在开放访问的模式下，用户根据平均最强信号的关联规则，可以与任一层服务节点相关联，因此用户服务节点的密度与干扰节点的密度是相同的.在第1种等价模式下，节点的密度为λT，等价功率Peq是在第k层用户所接受的有用信号不变的情况下得到的，因此，用户的服务节点的功率和干扰节点的功率可认为是相同的.

3.4 应用

通过前面的分析可知，在干扰总量等价的意义下，多层网络可以等价为一层网络.本部分说明这种等价在某些技术条件下的应用，包括异构网络使用SIC技术的性能分析，以及异构网络的SIR元分布分析.

(1)本文的等价方法，可以在使用SIC技术的多层网络分析中提供方便.文献[15]已经使用密度等价的方法分析了HIP网络中SIC技术对网络性能的影响.SIC技术需要接收端根据所接收到干扰的强弱进行排序，然后将最强的前N个干扰信号消除，再计算其SIR是否满足解码阈值要求.异构网络意味着每层传输节点的功率不同，密度不同，因此难以根据节点的距离进行排序.利用等价，首先将多层网络等价为一个具有唯一密度和唯一发送功率的单层网络.干扰信号的排序就变为单层网络中的处理，因为节点可以认为具有相同的功率，可以根据节点与用户之间的距离进行排序.此时，第n个最大干扰与用户的距离X满足

(3)

接收端消除掉最强的n个干扰后的成功传输概率为

此处，λi为接收端的等价干扰密度，fr(r)对应用户与发送端的距离的概率密度函数.

事实上，在多层混合网络模型中，如嵌入机器类型通信MTC链路的异构网络，使用SIC技术可用同样的分析方法.文献[16]分析了SIC技术在单层蜂窝网和D2D链路条件下的网络性能.与一般的异构网络不同，在嵌入MTC的异构网络中，用户面临的服务密度与干扰密度一般是不同的.例如在D2D嵌入多层蜂窝网的情形中，对蜂窝用户而言，只有蜂窝基站提供服务，而D2D节点只是作为干扰；同理，对D2D节点，蜂窝网的传输只能是干扰.因此上述公式，对蜂窝用户的等价干扰密度增加了D2D发送节点的密度.

根据命题1和命题2可知，在一般的多层异构网络中，加入SIC技术后，通过网络的哪一层来进行等价分析，对混合网络的性能是没有影响的.在混合的异构网络中，例如在嵌入D2D链路的多层蜂窝网络中，蜂窝网部分通过哪一层进行等价分析，其网络的覆盖概率是相同的，同样，D2D链路的成功概率也不会受某一层等价分析的影响.

(2)本文分析的随机等价还可以用于SIR元分布的分析中[18].所谓SIR元分布就是SIR的分布P(SIR>θ)的分布[19].在元分布的分析中，链路成功传输的可靠性与链路传输速度之间存在一定的折中[20].在多层异构混合网络中，通过等价的密度，就可以获得链路的速率控制参数θ，以满足特定的传输可靠性.在含有封闭访问层的网络中，例如嵌入MTC的多层蜂窝网中，蜂窝链路的SIR阈值与传输可靠性可以通过式(4)近似给出

(4)

此外，在一些有功率控制要求的多层异构网络中，可以通过网络等价将问题简化为单层网络中的问题，从而得出一些易分析的结果.例如，文献[17]对功率控制的SIR元分布是针对单层PPP网络模型的，通过随机等价就可以将其推广到多层网络中，这可作为本文工作扩展的一个方面.

未来的无线系统越来越呈现出异构性和混合性的特点，例如日趋成熟的5G通信的目标可支持大规模的异构性，例如eMBB,mMTC以及URLLC[21]，在分析这类网络的干扰和性能时，本文的等价方法可以提供便利.

4 仿 真

本部分给出以上分析的仿真结果，以验证本文方法的正确性.不失一般性，假设网络的每层节点构成一个独立的PPP，并具有特定的密度和发送功率.假设网络节点分布在一个100×100的矩形范围.

图1是一个等价功率计算的结果.我们假设两层网络的密度分别为λ1=20，λ2=30，P1∶P2=1∶2.假设P1从10变化到100，可以看出虽然由于网络节点分布的随机性，总的干扰呈现出波动，但等价功率产生的干扰总量和实际仿真的结果变化趋势是相同的.

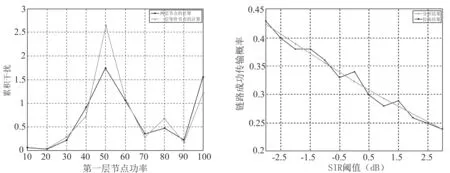
图1 等价功率的分析与仿真结果 图2 等价密度对覆盖概率的影响趋势的分析与仿真

图2～图5的仿真参数设置如下：网络包含3层分别为m层，p层和d层，假设m层和p层是开放访问，d层是封闭访问(即该层用户不能与其他层关联).每层的功率设置为Pm=200，Pp=100，Pd=50，对应每层节点的密度分别为λm=0.01,λp=0.02,和λd=0.04.假设信号传输的衰落服从均值为1的指数分布，路径损耗指数为4.考虑到节点分布的随机性对结果的影响，我们重复进行300次随机仿真试验，然后对结果进行算术平均.

图2是根据等价密度，对网络m层节点的覆盖率的计算.如果用户与网络其中一层节点相关联，则该用户的干扰来自3层不同功率的节点，我们仿真了该条件下的用户覆盖概率.假设链路成功传输的SIR阈值变化范围为-5～5 dB.同时，根据本文分析的等价密度的结果，可以计算出一个等价的单层网络的覆盖率，我们对此进行了比较，可以看出二者结果比较接近.

图3和图4是根据密度等价的原理，对混合结构的异构网络实施SIC技术的成功传输概率分析.为了说明问题，本文列出开放层(图3)和封闭层(图4)的用户在使用SIC之后，在成功消除掉1、2、3、4个最大干扰的情况下对成功传输概率的影响.可以看出，对于计算SIC技术对网络的影响，通过网络等价计算的结果，与仿真的结果比较吻合，这说明了密度等价的方法在该类问题分析中的正确性.

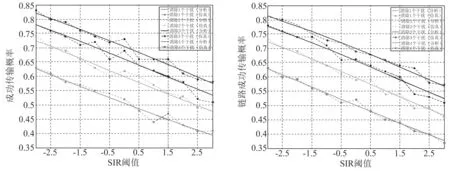
图3 等价密度用于开放访问层的SIC分析 图4 等价密度用于封闭访问层的SIC分析

对于混合结构的多层异构网络，在分析其SIR元分布的过程中，图5给出了根据链路传输可靠性的要求对m层节点SIR阈值进行设置，即速率控制的仿真.从图中可以看出随着对目标可靠性v的提高，SIR阈值必须适当下降才能保持相应的可靠性.

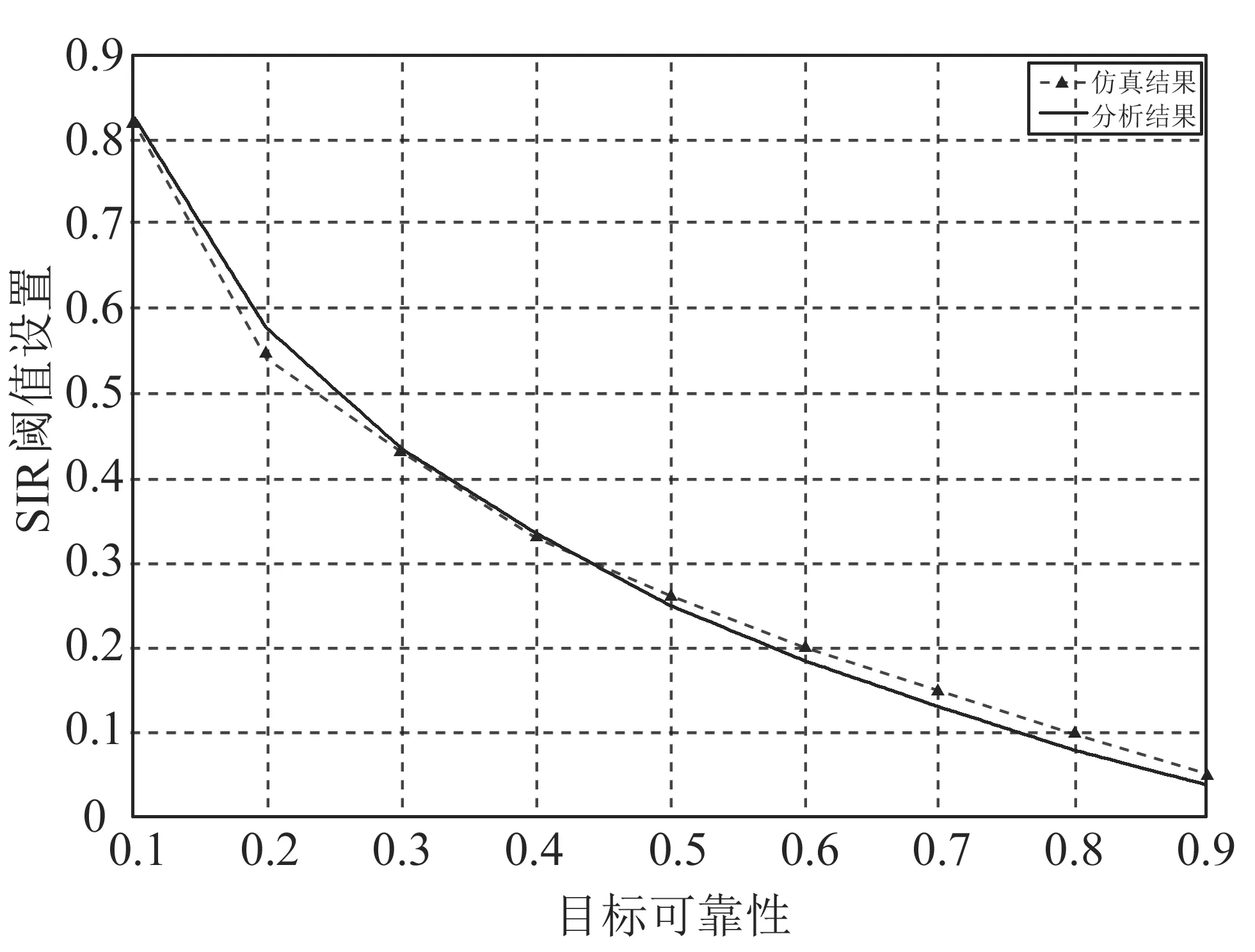
图5 多层混合网络中根据干扰等价分析速率控制和传输可靠性的关系

5 结 论

本文利用随机几何，分析了多层PPP分布的异构无线网络中的随机等价问题.随着技术的发展，未来无线网络的结构呈现出更显著的异构化和多样化，不利于网络性能的分析.在干扰总量等价的意义下，本文提出的第一种等价分析了多层网络在功率方面的等价性，将多层网络等价为一个具有固定密度和特定发送功率的单层网络.第二种等价根据网络不同层的功率标准，计算相应的等价密度.在此基础上，本文证明了针对不同层的网络等价并不影响网络性能.利用随机等价的方法，将多层网络简化为单层网络结构，可以将一些只适合于单层网络的结果扩展到多层网络，本文根据等价密度将SIC技术对多层网络的影响，和链路速率控制进行了分析.仿真结果证实了方法的可行性和准确性.