混水平正交试验的假设检验误差控制*

高鑫雨,赵胜利

(曲阜师范大学统计学院，273165，山东省曲阜市)

0 研究背景与意义

自20世纪20年代英国统计学家Fisher R A在农业生产中创立试验设计以来，试验设计已在各个领域得到广泛的发展，其主要任务是研究最优设计的构造以及对试验数据进行统计分析.著名统计学家Box G E P说过，假如有10%的工程师使用各种试验设计方法，产品的质量与数量都会得到很大提高[1].因子设计在各类试验中应用相当广泛，常用于研究各因子对试验指标是否具有显著影响.在实际问题中，影响试验指标的因子往往有多个，而当涉及的因子数较多时，因子的水平组合数会迅速增加，受试验条件的限制往往难以全部实施.正交设计则是安排多因子试验的一种高效的试验设计方法.方差分析是对因子进行显著性检验的常用方法，且方差分析需要满足3项基本假定：正态性、方差齐性和随机性.正态性和随机性在实际中容易得到满足，由于试验在实际操作时环境复杂，方差齐性通常得不到满足，因此在不同的处理组合下会有不同的试验误差方差，在这种情况下，采用方差分析对因子进行显著性检验会产生一定的误差，且检验犯第一类错误的概率可能与显著性水平产生偏离.

在实际试验中经常遇到试验因子的水平数不相等的情况，这种情况下实施试验需要用到混水平正交设计.混水平正交设计因为其灵活的水平组合在各种混水平试验中得到非常广泛的应用[1].

本文在不同处理组合下试验误差方差不等的情况下，考察混水平正交试验因子的显著性检验问题，从方差分析中F统计量的构造给出新的检验统计量，利用随机模拟的方法获得相应的临界值，分别通过传统的F检验与新检验方法检验各因子效应的显著性，模拟结果表明在试验误差方差不等时F检验犯第一类错误的概率严重偏离显著性水平，新的检验方法犯第一类错误的概率更精确.

1 基本概念与方法

1.1 混水平正交表的构造

对2水平正交表L8(27)通过并列法改造可以得到混水平正交表L8(4×24)，由于4水平因子的自由度为3，因此在2水平正交表中应该占3列，这3列的选法是：任取2列再加上其交互作用列，由此3列组成一个4水平列，4水平的对应法则如下：将任取的2列的4个数对对应4个水平，即：(1,1)→1,(1,2)→2,(2,1)→3,(2,2)→4.

此时4个数对各出现两次，不失一般性，取第1、2两列加上其交互作用列第3列组成一个4水平列，经过上述改造，即可得到混水平正交表L8(4×24)[1].

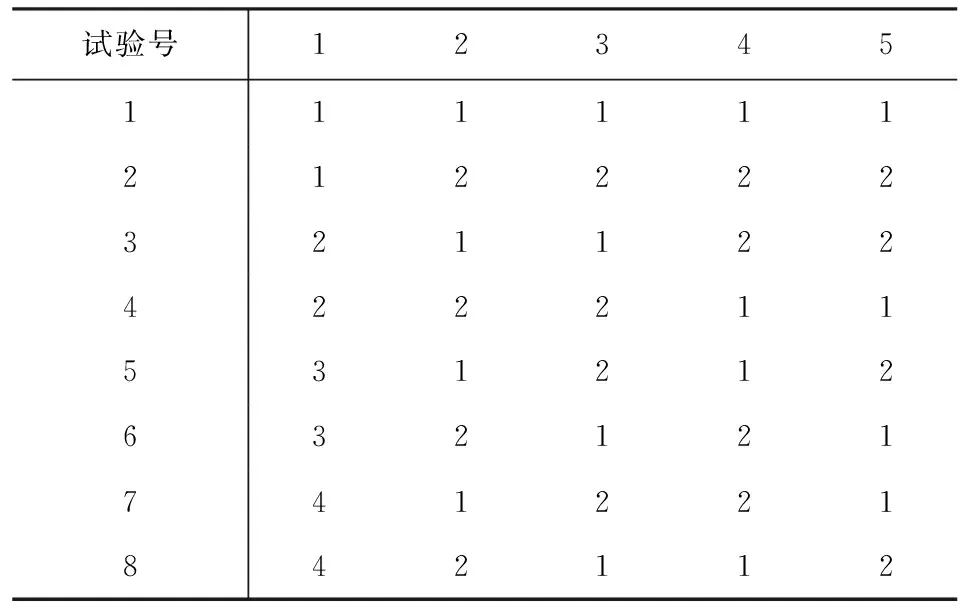
表1 L8(4×24)正交表

对2水平正交表L16(215)通过上述相同的方法改造可以得到混水平正交表L16(4×212)，此时4个数对各出现四次，不失一般性，仍取第1、2两列加上其交互作用列第3列组成一个4水平列，经过上述改造，即可得到混水平正交表L16(4×212).

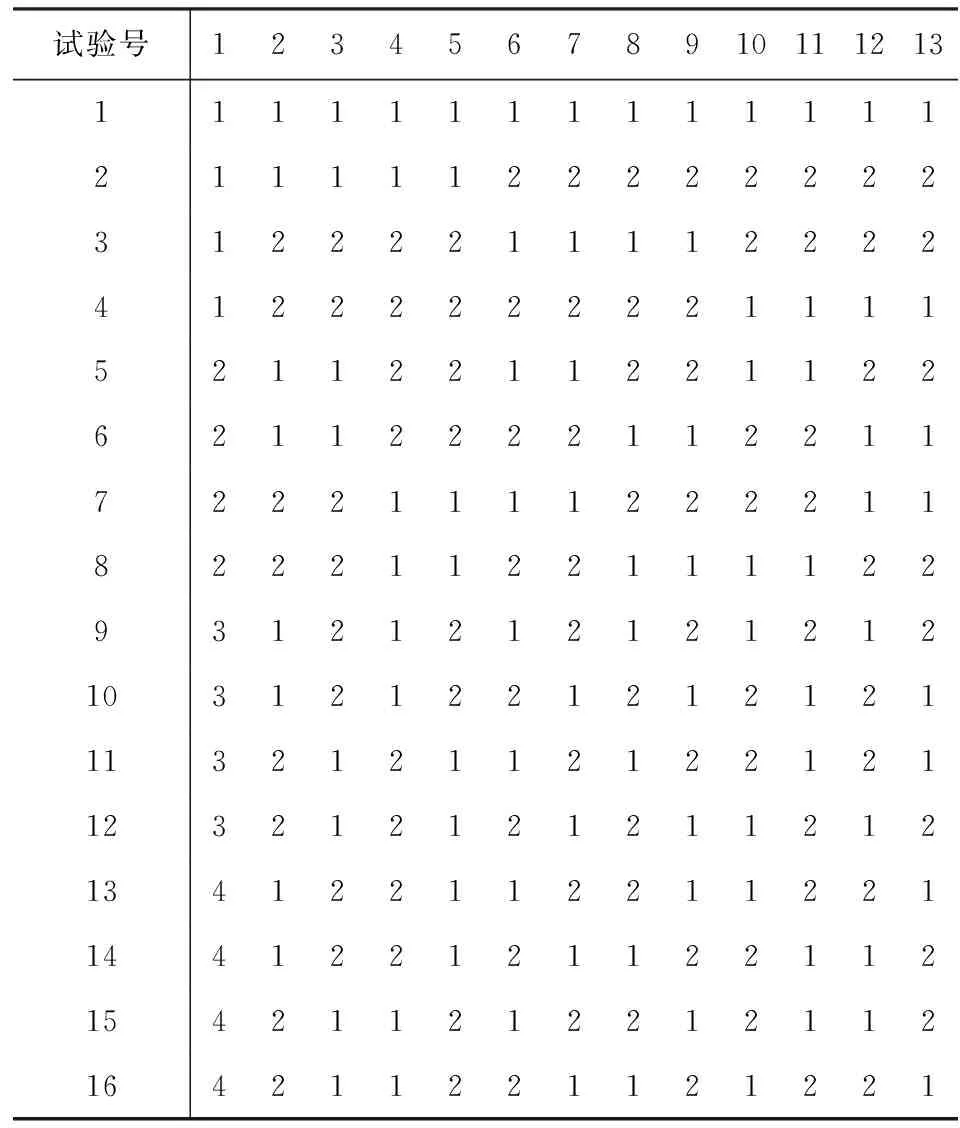
表2 L16(4×212)正交表

还可将2水平正交表L16(215)改造成混水平正交表L16(8×28)，由于8水平因子的自由度为7，因此在2水平正交表中应占7列，这7列的选法是：任取3列独立列再加上其交互作用列，由此7列组成一个八水平列，八水平的对应法则如下：将任取的3列的8个数对对应8个水平，即：

(1,1,1)→1,(1,1,2)→2,(1,2,1)→3,(1,2,2)→4,

(2,1,1)→5,(2,1,2)→6,(2,2,1)→7,(2,2,2)→8.

此时8个数对各出现2次，不失一般性，取第1、2、4列加上其交互作用列第3、5、6、7列组成一个8水平列，经过上述改造，即可得到混水平正交表L16(8×28).

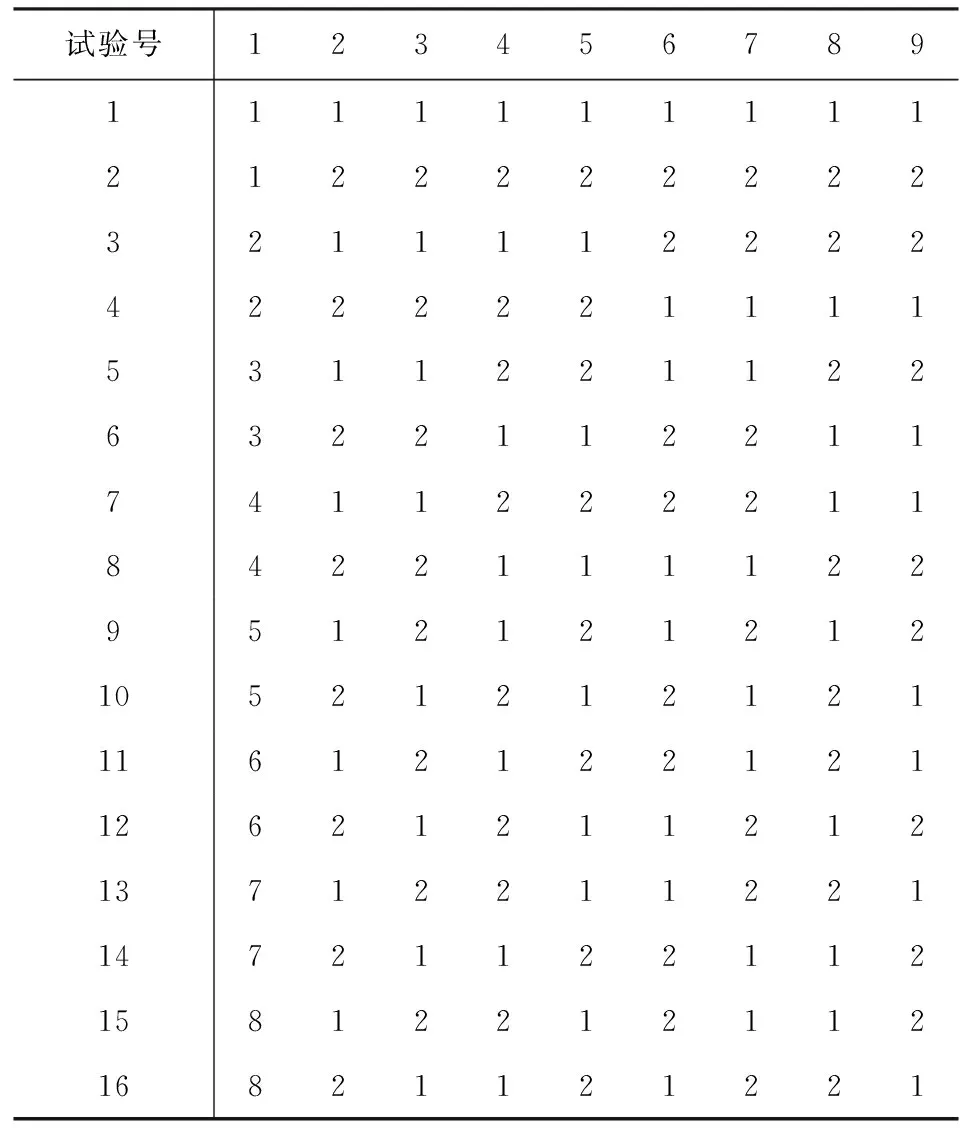
表3 L16(8×28)正交表

1.2 重复正交试验的方差分析

1．2．1 统计模型

考虑因子的水平数不等的等重复试验，利用正交表进行试验设计，设正交表为Ln(qp)，假设有n个处理组合，在同一处理组合下重复进行m次试验.考虑如下线性统计模型

yij=ui+εij，i=1,…,n,j=1,…,m，

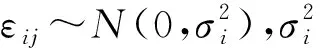
1．2．2 显著性检验

为检验各因子的效应是否显著，对如下假设作出检验

由于存在重复试验，因此如果把每一处理组合下的数据结果看作一个组，则组内的平方和反应的是纯误差，可用组内平方和度量

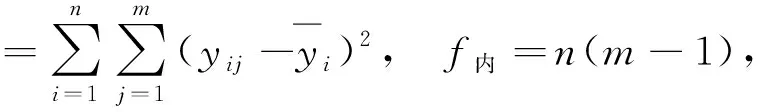
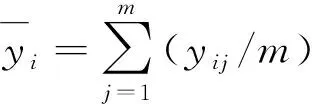
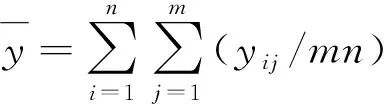
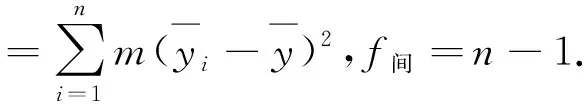
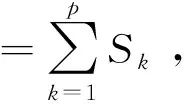
fk=q-1,

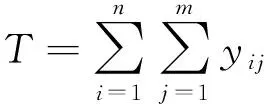
由Cochran定理知，当原假设成立即因子的效应为0，并且各试验误差的方差相等时，S内/σ2～χ2(n(m-1))，Sk/σ2～χ2(p-1)，且S内与Sk相互独立，故

当统计量Fk≥F1-α(p-1,n(m-1))时，认为在显著性水平α下因子是显著的，即认为该因子的效应不为0，其中F1-α是相应自由度的F分布的1-α分位数[1].

由于改造后的表仍是正交表，设计仍是正交设计，因此，平方和分解式与方差分析与改造前相同，并且可以用改造前的正交表计算混水平试验的各列平方和，只需按表头设计计算因子在改造前的正交表中所占列的平方和.

1.3 改进的显著性检验

方差分析是对因子进行显著性检验的常用方法，然而方差分析需要假定不同处理组合下具有相同的试验误差方差，由于试验在实际操作时环境复杂，因此在不同的处理组合下会有不同的试验误差方差，在这种情况下，采用方差分析的方法对因子进行显著性检验会产生一定的误差，且检验犯第一类错误的概率可能与显著性水平产生偏离，从而因子的显著性检验容易发生误判，为此，从F统计量的构造出发给出新的检验统计量，并采用随机模拟的方法获得相应的临界值.

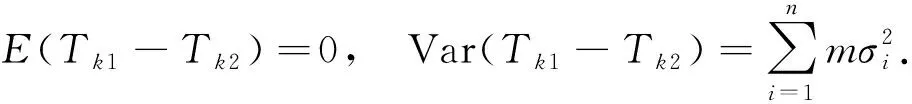
将F统计量变形得到

此时Fk的分子服从χ2(1)，接下来考虑Fk分母的分布.注意到

因此可以将Fk的分母变形为

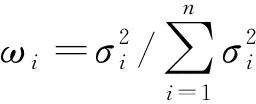
由上述推导过程可知，在原假设成立的条件下，当不同处理组合下试验误差的方差不相等时，变形后的F统计量的分子服从χ2(1)，分母是以试验误差方差为权重的n个χ2(m-1)的加权和.

对于由2水平正交表改造的混水平正交试验，可以采用改造前的正交表计算各列平方和，只需按表头设计将因子在改造前的正交表中所占列的平方和相加，由卡方分布的可加性知，变形后的F统计量分子服从χ2(a)，其中卡方分布的自由度a取决于因子在改造前的正交表中所占列的列数，分母的分布保持不变.

显然，此时的检验统计量不再服从F分布，如果仍用F1-α(p-1,n(m-1))作为显著性检验的临界值是不合理的，因子的显著性也容易发生误判，由于检验统计量的精确分布很难确定，因此采用随机模拟的方法来确定检验的临界值，随机模拟过程如下：

步骤2 对于l=1,…,M;

步骤2.1 生成一个χ2(a)的随机变量Ul;

步骤2.2 生成n个相互独立的χ2(m-1)的随机变量Vl1,…,Vln;

步骤2.3 计算检验统计量

步骤3 取显著性水平α，计算检验统计量的分位数qα.

2 结果与分析

以3个由2水平正交表改造的混水平正交表为例，在不同处理组合的试验误差方差相等和不等两种情况下，分别利用F检验和改进后的新检验方法对因子的显著性检验进行模拟对比，随机模拟过程重复10 000次.

2.1 试验误差方差相等时的模拟对比

假设试验1需要考察5个因子A、B、C、D、E的显著性，其中因子A是4水平因子，因子B、C、D、E是4个2水平因子，为此，选用混合水平正交表L8(4×24)进行试验，置因子A在正交表的4水平列上，即由正交表L8(27)的第1，2，3列组成的列，再将因子B、C、D、E安排在剩余的2水平列上，表头设计如表4.

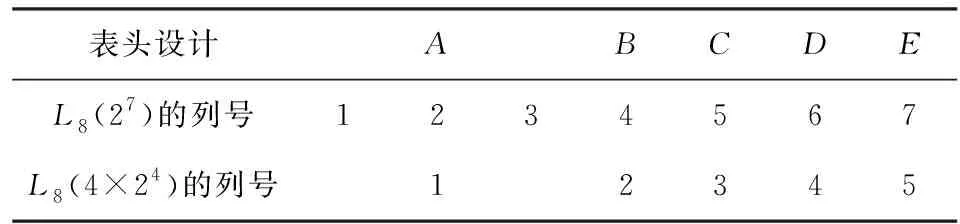
表4 试验1的表头设计

假设不同处理组合下的试验误差具有相同的方差2，总平均为10，因子A与因子D是显著因子，并且βA=0.4,βD=0.65,因子B、C、E均为不显著因子，即因子B、C、E的效应为0，因此试验1的统计模型为yij～N(10+0.4A+0.65D,2),其中A和D根据因子的水平组合取±1.假设在同一处理组合下重复进行若干次试验，取显著性水平为0.05，分别利用F检验与改进后的新检验方法来检验各因子效应的显著性，得到拒绝原假设的百分比，如表5所示.

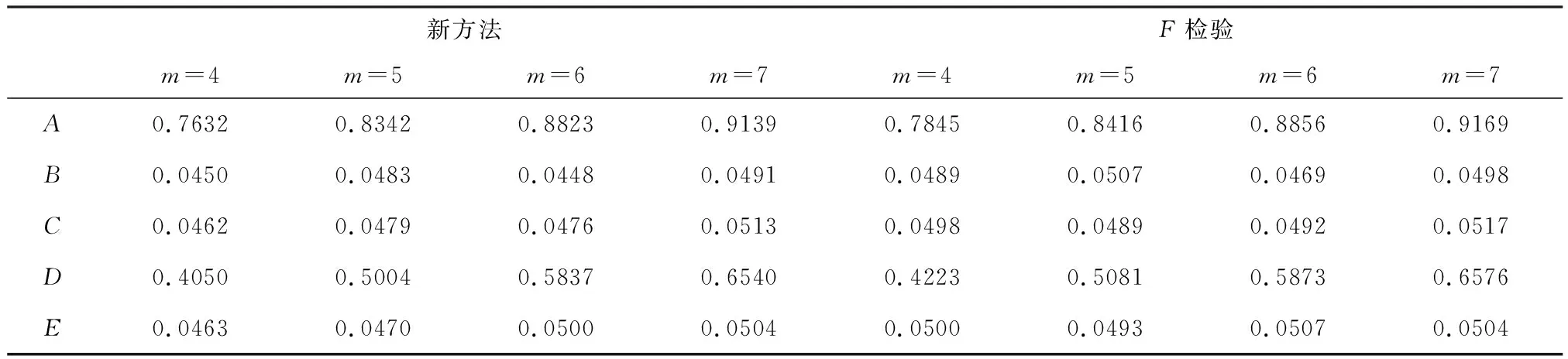
表5 试验1在5%水平下拒绝原假设的百分比

假设试验2需要考察因子A、B、C、D、E、F、G的显著性，其中因子A是4水平因子，因子B、C、D、E、F、G是二水平因子，假定根据专业知识还需考察交互作用A×B与A×C,为此，选用混合水平正交表L16(4×212)进行试验.

置因子A在正交表的4水平列上，即由正交表L16(215)的第1，2，3列组成的列，再将因子B安排在第4列，交互作用A×B安排在第5，6，7列，即由因子A在L16(215)所占的3列与B所在列的交互列组成的列，再将因子C安排在第8列，交互作用A×C安排在第9，10，11列，最后将因子D、E、F、G依次安排在剩余的列，综上可得表头设计如表6.

表6 试验2的表头设计

假设不同处理组合下的试验误差具有相同的方差2，总平均为10，因子A、B以及交互作用A×B与A×C显著，并且各个显著因子的效应分别为βA=0.3,βB=0.55,βA×B=0.35,βA×C=0.2,因子D、E、F、G均为不显著因子,因此，试验2的统计模型为yij～N(10+0.3A+0.55B+0.35AB+0.2AC,2),其中A、B、AB及AC根据因子的水平组合取±1，取显著性水平0.05，分别利用F检验与改进后的新检验方法来检验各因子效应的显著性，得到拒绝原假设的百分比，如表7所示.

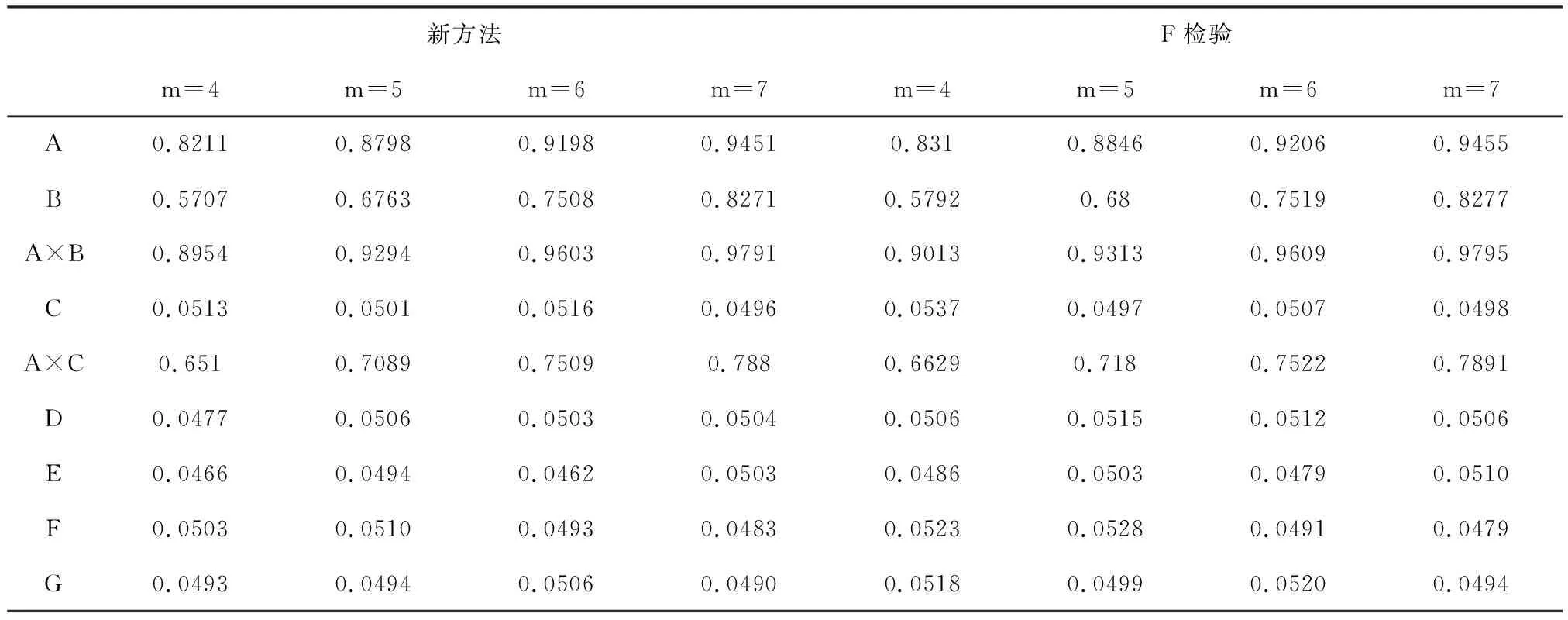
表7 试验2在5%水平下拒绝原假设的百分比

假设试验3需要考察因子A、B、C、D、E、F、G的显著性，其中因子A是8水平因子，因子B、C、D、E、F、G是2水平因子，假定试验不需要考察交互作用，为此，选用混合水平正交表L16(8×28)进行试验.置因子A在正交表的八水平列上，再将因子B、C、D、E、F、G依次安排在2～7列，可得表头设计如表8.

表8 试验3的表头设计

假设不同处理组合下的试验误差具有相同的方差2，总平均为10，仅因子A是显著因子，且因子A的效应为βA=0.2,因子B、C、D、E、F、G均为不显著因子，即因子的效应为0，因此，试验3的统计模型为yij～N(10+0.2A,2),其中A根据因子的水平组合取±1，取显著性水平为0.05，分别利用F检验与改进后的检验方法来检验各因子效应的显著性，得到拒绝原假设的百分比，如表9所示.

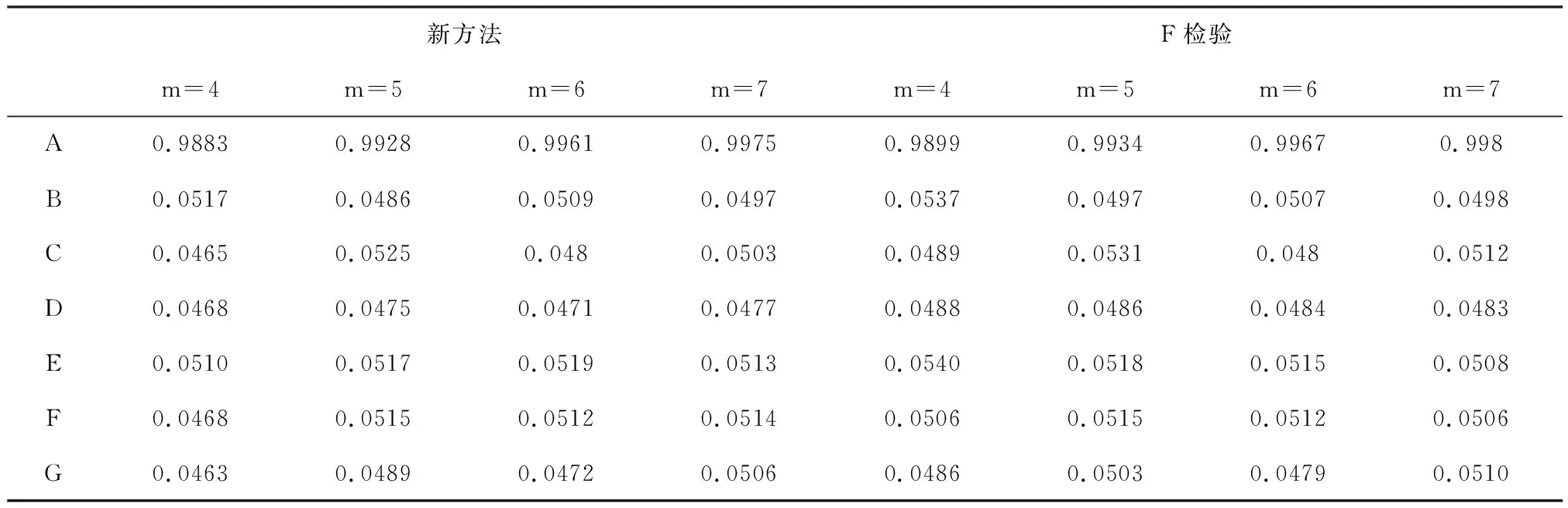
表9 试验3在5%水平下拒绝原假设的百分比

由表5、表7、表9的模拟结果对比可知，当不同处理组合下的试验误差方差相等时，传统的F检验与改进后的新检验方法犯第一类错误的概率均接近显著性水平0.05，且随着重复次数的增加犯第一类错误的概率相对稳定.综上，在试验误差方差相等的情况下，对混水平正交试验因子的显著性作检验，改进后的新检验方法与F检验均有较精准的误差控制.

2.2 试验误差方差不相等时的模拟对比

假定试验4与试验1所考察的因子以及因子效应的大小相同，但试验4在不同处理组合下的试验误差方差不相等，即试验误差方差与处理组合有关.假定试验4的试验误差方差受因子B、C、D的影响，且其系数分别为0.5、0.55、0.4，则试验4的统计模型为

yij～N(10+0.4A+0.65D,

exp(0.5B+0.55C+0.4D)),

取显著性水平0.05，分别利用F检验与改进后的新检验方法来检验各因子效应的显著性，得到拒绝原假设的百分比，模拟对比的结果如表10所示.

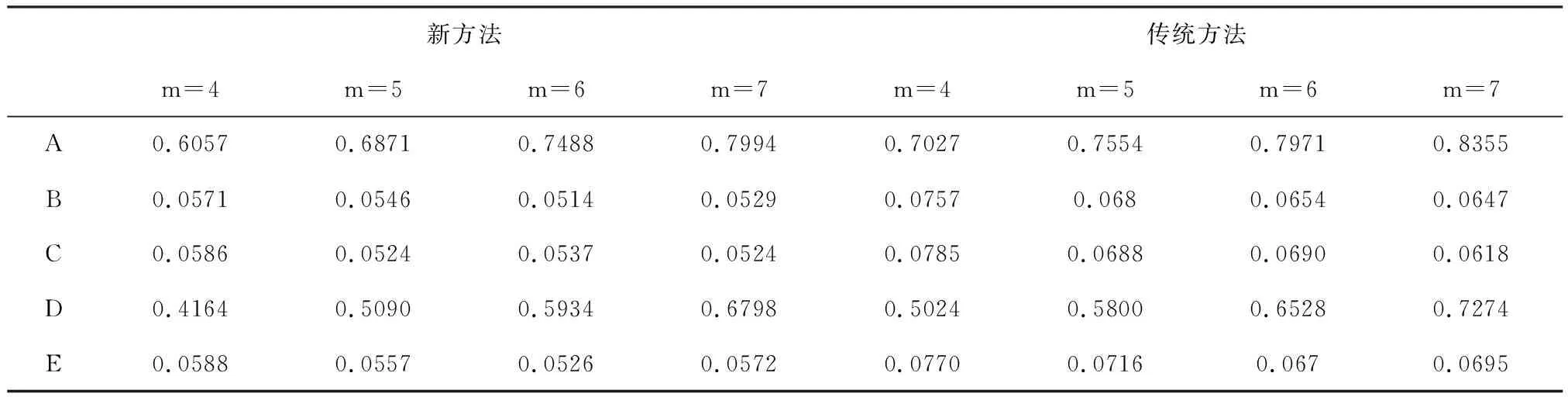
表10 试验4在5%水平下拒绝原假设的百分比

假定试验5与试验2所考察的因子以及因子效应的大小相同，但试验5在不同处理组合下的试验误差方差不相等，即试验误差方差与处理组合有关.假定试验5的试验误差方差受因子A、C以及交互作用A×B的影响，且其系数分别为0.45、0.25、0.5，则试验5的统计模型

yij～N(10+0.3A+0.55B+0.35AB+0.2AC,

exp(0.45A+0.25C+0.5AB)),

取显著性水平0.05，分别利用F检验与改进后的新检验方法来检验各因子效应的显著性，得到拒绝原假设的百分比，模拟对比的结果如表11所示.

表11 试验5在5%水平下拒绝原假设的百分比

假定试验6与试验3所考察的因子以及因子效应的大小相同，但试验6在不同处理组合下的试验误差方差不相等，即试验误差方差与处理组合有关.假定试验6的试验误差方差仅受因子A的影响，且其系数为0.45，则试验6的统计模型

yij～N(10+0.2A,exp(0.45A)),

则在显著性水平0.05下，分别利用F检验与改进后的新检验方法来检验各因子效应的显著性，得到拒绝原假设的百分比，模拟对比的结果如表12所示.

表12 试验6在5%水平下拒绝原假设的百分比

由表10～表12的模拟结果对比可知，当不同处理组合下的试验误差方差不相等时，传统的F检验犯第一类错误的概率严重偏离0.05，从而因子效应的显著性容易发生误判，改进后的新检验方法犯第一类错误的概率几乎接近显著性水平0.05，且随着重复次数的增加犯第一类错误的概率更稳定.综上，在试验误差方差不等的情况下，对混水平正交试验因子的显著性作检验，改进后的新检验方法比F检验有更精准的误差控制.

3 讨 论

因子设计在各类试验中应用相当广泛，用于研究各因子对试验指标是否具有显著影响.在实际问题中，影响试验指标的因子往往有多个，要考察它们就要用到多因子试验设计，正交设计就是安排多因子试验的一种高效的试验设计方法.方差分析中的F检验是对因子进行显著性检验的常用方法，然而方差分析需要假定不同处理组合下具有相同的试验误差方差，由于试验在实际操作时环境复杂，因此在不同的处理组合下会有不同的试验误差方差，在这种情况下，采用方差分析对因子进行显著性检验会产生一定的误差.

为此，从方差分析中F统计量的构造给出新的检验统计量，通过随机模拟的方法获得相应的临界值，以3个混水平正交表为例，在不同处理组合的试验误差方差相等和不等两种情况下，分别利用F检验和改进后的新检验方法对因子的显著性检验进行模拟对比，得到结论如下：

当不同处理组合下的试验误差方差相等时，考察等重复的混水平正交试验的因子显著性检验问题，传统的F检验与改进后的新检验方法犯第一类错误的概率均接近显著性水平0.05，且随着重复次数的增加犯第一类错误的概率相对稳定，改进后的新检验方法与F检验均有较精准的误差控制.当不同处理组合下的试验误差方差不相等时，传统的F检验犯第一类错误的概率严重偏离0.05，从而因子效应的显著性容易发生误判，改进后的新检验方法犯第一类错误的概率几乎接近显著性水平0.05，且随着重复次数的增加犯第一类错误的概率更稳定，因此，改进后的新检验方法比F检验能更精准的控制检验误差.

综上可知，F检验对方差齐性的偏离较为敏感，在考察等重复的混水平正交试验因子的显著性检验问题时，方差齐性检验十分必要，若不同处理组合下的试验误差方差不全相等，则应采用提出的新检验方法判断因子效应的显著性，否则会产生一定误差.