区间Pythagorean模糊几何加权Bonferroni平均算子及其应用*
2021-08-26蒋莹莹段鹏举赵丽莎
蒋莹莹,段鹏举,赵丽莎
(宿州学院数学与统计学院,234000,安徽省宿州市)
0 引 言
1965年Zadeh[1]提出模糊集理论,用介于[0,1]的隶属度刻画信息的模糊程度,并研究了其在人工智能、运筹管理等领域的应用.1986年Atanassov[2]提出直觉模糊集,拓宽模糊信息形式.2014年Yager[3]指出虽然直觉模糊数的隶属度与非隶属度都介于[0,1],但决策过程中部分模糊数据的隶属度与非隶属度的和可能大于1,为克服此情况提出了隶属度与非隶属度的平方和小于1的毕达哥斯模糊集(PFS).Zhang[4]提出了区间毕达哥拉斯模糊集(IVPFS),丰富了数据信息的模糊性和不确定性表达途径.Yager[5]构造了毕达哥拉斯模糊加权平均算子及有序加权几何算子并证其特性;李进军[6]等将幂加权平均/幂几何/Heronian平均算子推广到IVPFS.在实际决策过程中,考虑到变量间的交互关联可能会影响评价的结果,Yager[7]等提出了Bonferroni 平均(BM)算子,该算子能反映变量间的关联性,把多个变量集结成一个变量提升决策的准确程度;于倩和周晓辉[8-9]等在犹豫模糊集李晓然[10]在犹豫模糊集下研究了最优加权Bonferroni几何平均算子;
张金波[11]在直觉模糊集下研究了可退化的加权Bonferroni几何平均算子;Liang[12]和Peng[13]等把IVPFS与Bonferroni平均算子相结合进行研究;并讨论其特性.
借助Bonferroni平均算子能够描述决策属性间的相互关联的优势,在该优势的基础上增加属性值的几何特性来规避奇异值,使决策数据更加平稳.另外,考虑各属性值的权重的影响,调整属性权重构造一种不同于最优加权Bonferroni几何平均算子和可退化的加权Bonferroni几何平均算子的基于区间毕达哥拉斯模糊集的几何加权Bonferroni平均算子,把几何加权Bonferroni平均算子拓展到区间毕达哥拉斯模糊环境,解决区间毕达哥拉斯模糊多属性决策问题.
1 预备知识
1.1 (区间)毕达哥拉斯模糊集
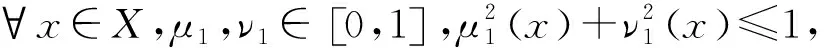



定义4[4]设α=([μL,μU],[νL,νU])为IVPFN,其得分函数与精确函数分别为
由定义,以下给出IVPFN排序方法:
(1)若sα1 (2)若sα1>sα2,则α1≻α2; (3)若sα1=sα2,则 1)若hα1 2)若hα1>hα2,则α1≻α2; 3)若hα1=hα2,则α1=α2. 定义5[14]设p,q≥0,ai≥0(i=1,2,…,n)为实数集,若 GBp,q(a1,a2,…,an) 称函数GBp,q为几何Bonferroni平均(Geometric Bonferroni Mean,GBM)算子. GBM算子满足以下性质. 性质1(幂等性) 设ai为非负实数集,如果有ai=a(i=1,2,…,n),则有GBp,q(a1,a2,…an)=a. 性质2(有界性) 设ai为非负实数集,如果有a-=min(ai),a+=max(ai),则有 a-≤GBp,q(a1,a2,…an)≤a+. 性质4(单调性) 设ai(i=1,2,…,n),bi(i=1,2,…,n)为非负实数集,如果存在∀i,且ai≤bi,则有 GBp,q(a1,a2,…an)≤GBp,q(b1,b2,…bn). (α1,α2,…,αn) 继而得 即([μL,μU],[νL,νU])是IVPFN. (1)幂等性. 若αi=α(i=1,2,…,n),则IVPFGBMp,q(α1,α2,…,αn)=IVPFGBMp,q(α,α,…,α)=α; (2)置换不变性. 设(β1,β2,…,βn)是(α1,α2,…,αn)的任一置换,则 IVPFGBMp,q(α1,α2,…,αn)=IVPFGBMp,q(β1,β2,…,βn); IVPFGBMp,q(α1,α2,…,αn)≤IVPFGBMp,q(α1′,α2′,…,αn′). 证明(1)由αi=α(i=1,2,…,n),有 (2)由(β1,β2,…,βn)是(α1,α2,…,αn)的置换,则有 (3)由 可证同理IVPFGBMp,q(α1,α2,…,αn)≤δ+,即得证. (4)设 IVPFGBMp,q(α1,α2,…,αn)=([μL,μU],[νL,νU]), IVPFGBMp,q(α1,α2,…,αn)≤IVPFGBMp,q(α1′,α2′,…,αn′). 证明类似定理1. Step3 利用得分函数计算综合评价值ηi的得分值sηi;进行排序择优. 某旅游公司为顾客提供私人订制游玩路线A={A1,A2,A3},顾客的考虑因素有C={c1,c2,c3,c4}其中c1(安全程度)、c2(住行舒适度)、c3(成本费用)、c4(景色吸引程度),各指标的权重向量为ω=(0.3,0.2,0.24,0.26)T.顾客给出各方案在区间毕达哥拉斯模糊集下4个属性评价值构成的决策矩阵E=(αij)3×4. 表1 决策矩阵 表2 规范决策矩阵 η1=([0.883 4,0.919 2],[0.462 2,0.554 9]), η2=([0.911 2,0.947 6],[0.465 2,0.556 4]), η3=([0.882 4,0.917 2],[0.329 7,0.441 7]). Step3 利用定义4计算综合评价值ηi的得分值sηi: sη1=0.5519;sη2=0.6011;sη3=0.6580. 可得A3≻A2≻A1,即A3最优. 文中算法不仅侧重各属性因素对决策的影响,并且考虑了属性间的关联性、几何特性及权重的刻画,避免了在决策过程中属性奇异值的影响优化属性值的有效性,拓宽决策领域把GBM算子融合到IVPFS中提出IVPFGBM算子与IVPFGWBM算子,证明其幂等性、置换不变性等性质在IVPFS环境下依然成立;此外再构建IVPFS基于IVPFGWBM算子的多属性决策方法,在IVPFS数域内提出了新算子及新的模糊决策方法.1.2 几何Bonferroni平均(GBM)算子

2 IVPFGBM算子与IVPFGWBM算子
2.1 IVPFGBM算子



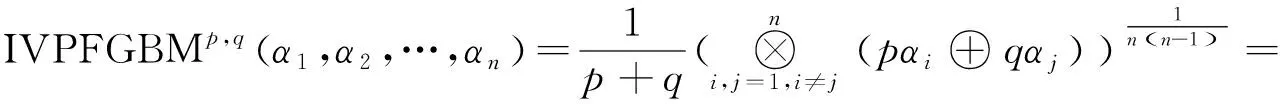




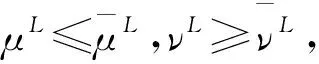
2.2 IVPFGWBM算子



3 基于IVPFGWBM算子的多属性决策方法
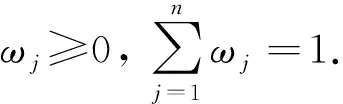
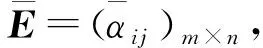
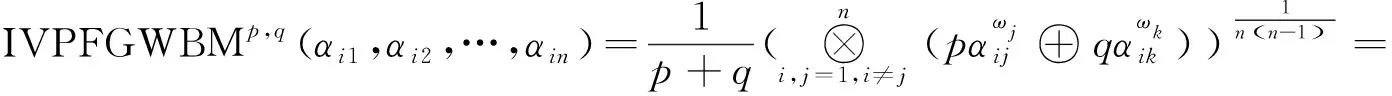
4 案例分析



5 总 结
