一种非线性金融系统的力学分析及基于有限时间LaSalle不变集的混沌控制

陈嘉琦，仓诗建，薛 薇

(1.天津科技大学电子信息与自动化学院，天津300222；2.天津科技大学艺术设计学院，天津300222)

金融系统是关于资金集中与分配的一个体系，是国家经济运行的核心部分，维护好金融系统的稳定运行和对金融系统紊乱进行有效地预测和控制对国家经济宏观调控非常重要，同样也是众多学者研究的热点.金融系统中投资需求与利率等因素[1]之间的相互影响，导致系统状态变化呈现复杂的动态特性.原本稳定的金融市场可能因某一个或几个因素的微小变化而出现停滞、混乱情况，甚至出现金融危机[2]，这种现象是金融系统非线性动态特性的典型反应.

揭示金融系统的发展规律，应当深入研究系统内部复杂结构.已有很多学者提出并研究了一些非线性金融模型.Kopel[3]研究了古诺双寡头模型的复杂动力学行为，Wu等[4]设计了关于古诺双寡头模型的控制方法，Lorenz等[5]分析了 Goodwins非线性加速模型的吸引子和吸引盆等.其中，研究较多的金融模型是一种非线性金融模型[6-7]，数学表达式为

式中：参数a,b,c ∈ R+，分别代表储蓄量、单位投资成本、商品需求弹性；状态变量 x,y,z ∈ R ，分别代表利率、投资需求、价格指数.由系统(1)可知，投资需求与储蓄量的大小关系，以及物价的结构调整都影响着x的变化，y的变化与利率和单位投资成本成反比，与投资率成正比；而z的变化既受通货膨胀率的影响，又受商品市场供求矛盾的调控.

针对系统(1)及其衍生的金融混沌系统，研究人员研究了系统控制的方法和分岔[7-13]，以及将系统(1)扩至 4D超混沌系统并研究系统中存在的复杂特性[14-16].Son等[8]考虑了时滞反馈项分别对不同变量的影响和对全部变量的影响.Gao等[12]讨论了时滞反馈系统 Hopf分岔的条件.Zheng等[14]利用一个异结构的4D超混沌系统对4D超混沌金融系统进行了投影同步研究.Zhang等[15]分析了4D超混沌金融系统的有界性.但是，大部分研究都只针对系统本身作理论分析和仿真验证，却很少结合实际情况.

本文将非线性金融系统分解成Kolmogorov系统形式，根据不同的力矩组合，从力学角度对该系统进行能量分析，并结合金融市场分析解释系统中状态变量和参数间的相互影响.为抑制金融系统的混沌行为，将有限时间理论和 LaSalle不变集定理进行结合，提出一种新的混沌控制方法.在理论分析的基础上借助数值仿真，将混沌状态的金融系统有效控制到稳定状态，从而达到对金融系统混沌行为的有效控制.

1 系统平衡点分析及混沌行为

当参数(a,b,c)满足 c -b - abc≤ 0 时，系统(1)存在单一平衡点 S1= ( 0,1/b, 0)；而当 c -b - abc＞0 时，系统(1)则存在 3个不同的平衡点 S1= ( 0,1/b, 0)，当参数(a,b,c)取不同值时，系统(1)会呈现不同的运动状态，例如周期运动、混沌等.特别当系统(1)选择初始条件 I0= ( 3,1,5)，参数集(a,b,c) = ( 1,0.2,1.1)时，可得到系统的3个Lyapunov指数值为 ( L E1, L E2, L E3)=(0.067,0,-0.628).由于 LE1＞0，这表明系统(1)处于混沌状态，相轨迹如图1所示.

图1 参数集(a,b,c ) = (1 ,0.2,1.1)时系统(1)的相图Fig.1 Phase diagram of system(1)parameter set (a,b,c)=(1,0.2,1.1)

2 系统力学分析

系统(1)的混沌行为已得到深入研究，作为具有实际意义的非线性系统，每个状态变量和参数都有其对应的实际物理意义.分析它们的变化对系统本身混沌现象的影响是研究整个系统混沌现象的重要基础.将系统(1)转换成Kolmogorov型系统后，其状态变量和参数仍具有各自对应的原始物理意义.

通常Kolmogorov型系统形式为

式中：X ={x,y,z}T表示状态变量，{·,·}表示李代数结构，力矩{X,H}表示保守力矩.正对角矩阵ΛX表示耗散力矩，f表示外力矩.

将系统改写成Kolmogorov系统的形式为

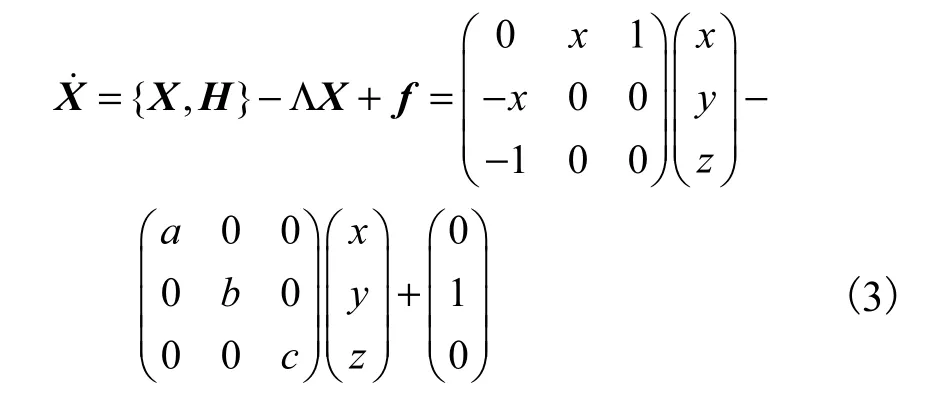
其中：X ={x,y,z}T，Λ = d iag{a,b,c}， f ={0,1,0}T.保守项{X,H}包括惯性力矩 K和内力矩 U，即H = K + U.根据式(3)不难得到系统的 Hamilton能量函数为

通过研究不同力矩组合对系统动力学特性的影响，进而探索系统(1)产生混沌现象的机制.

2.1 系统仅包含保守力矩

当系统(1)仅包含惯性力矩(动能)和内力矩(势能)时，有= { X ,K}+ { X ,U} = { X ,H}，对应的方程为

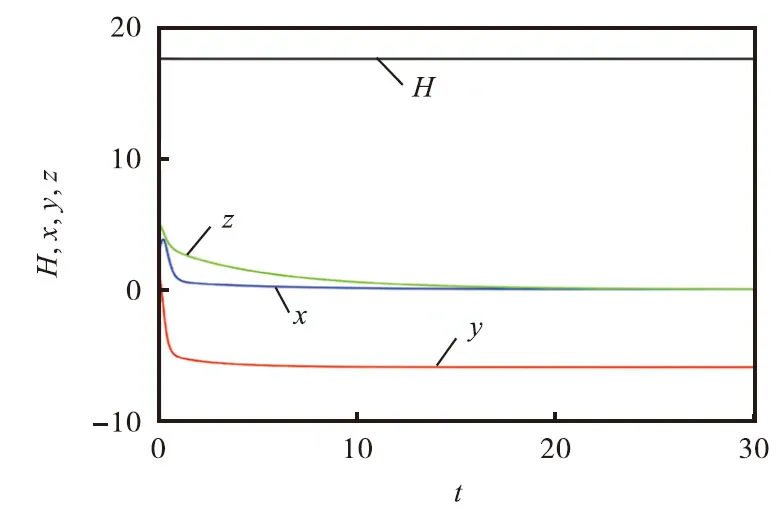
图2 初始值为 I0时，系统(5)状态变量 x、y、z及Hamilton能量H的时序图Fig.2 Time sequence diagram of the state variables x，y，z nd Hamilton energy H of the system(5) when the initial value is I0

2.2 系统包含保守力矩和耗散力矩

选取系统的 Hamilton能量函数H作为 Lyapunov函数，那么关于时间的导数为

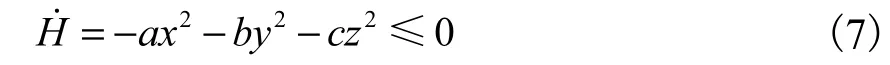
根据Lyapunov稳定性理论可知，系统(6)是稳定的，而且所有状态变量渐近收敛到 0.另一方面系统(6)的散度为

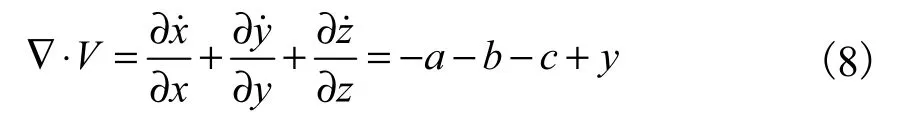
由于参数(a,b,c)均为正实数，当t→+∞时，由式(8)可知，系统(6)相空间的体积趋近于0.系统(6)的利率x，投资需求y和价格指数z都趋近 0.系统(6)的相轨迹、状态变量和 Hamilton能量变化规律如图3所示.此时，金融系统陷入完全停滞僵化的状态，经济市场缺少活力.

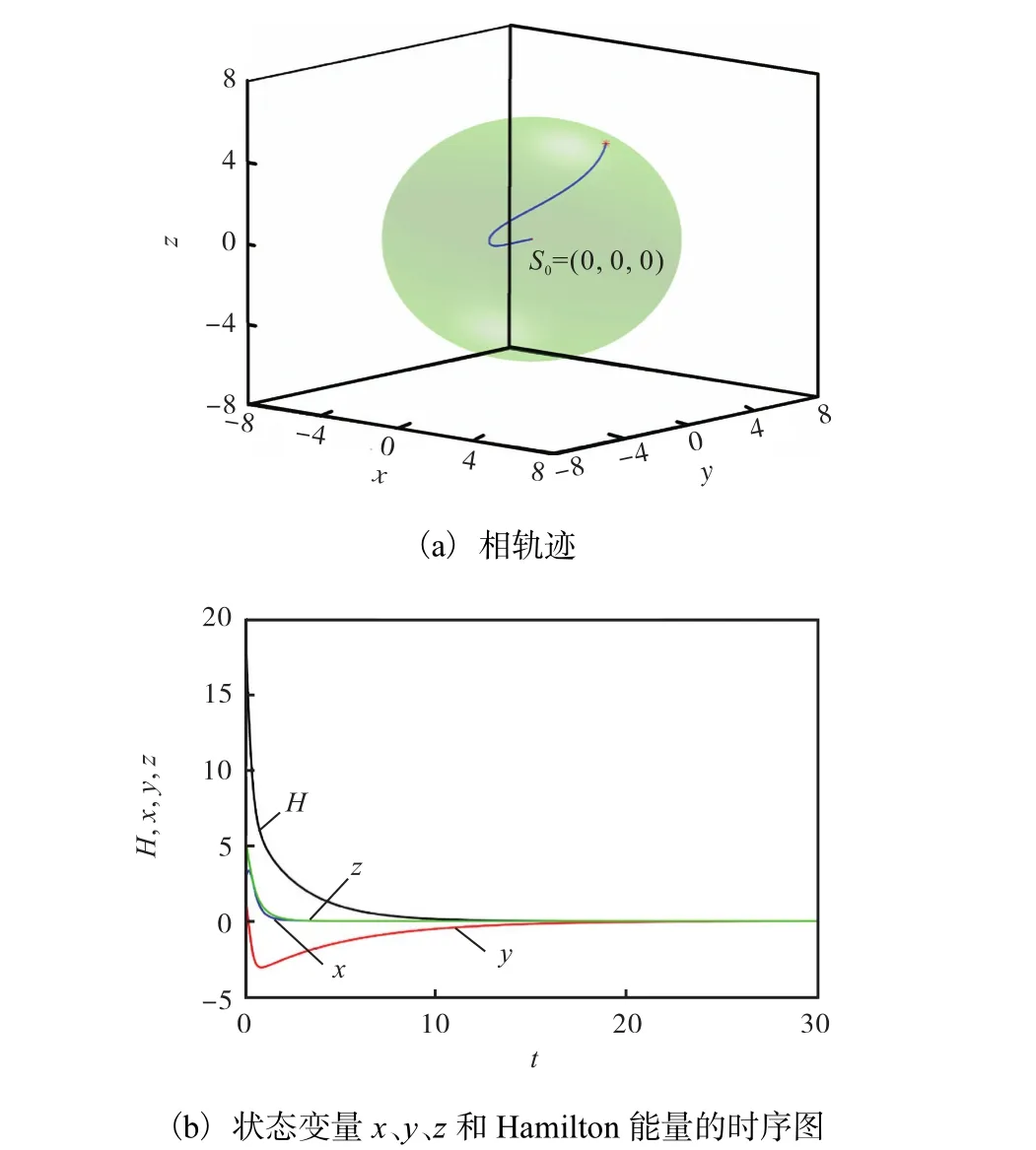
图3 系统(6)的动态特性Fig.3 Dynamic characteristics of the system(6)

2.3 系统包含保守力矩和外力矩

此时，外力矩 f中的投资率 1相当于一个外部强激励，f的存在极大地提升了经济市场的活力，但状态变量的运动变得没有规律，系统进入混沌状态.其Hamilton能量变化H˙=y，投资需求y由资本边际效率(预期增加一个单位投资可得到的利润率)和利率的对比关系决定.能量2/2 H=y 的吸收和释放随投资需求y的不规则运动而交错增减，是有限区域内的混沌.系统的相轨迹和能量变化规律如图4所示.

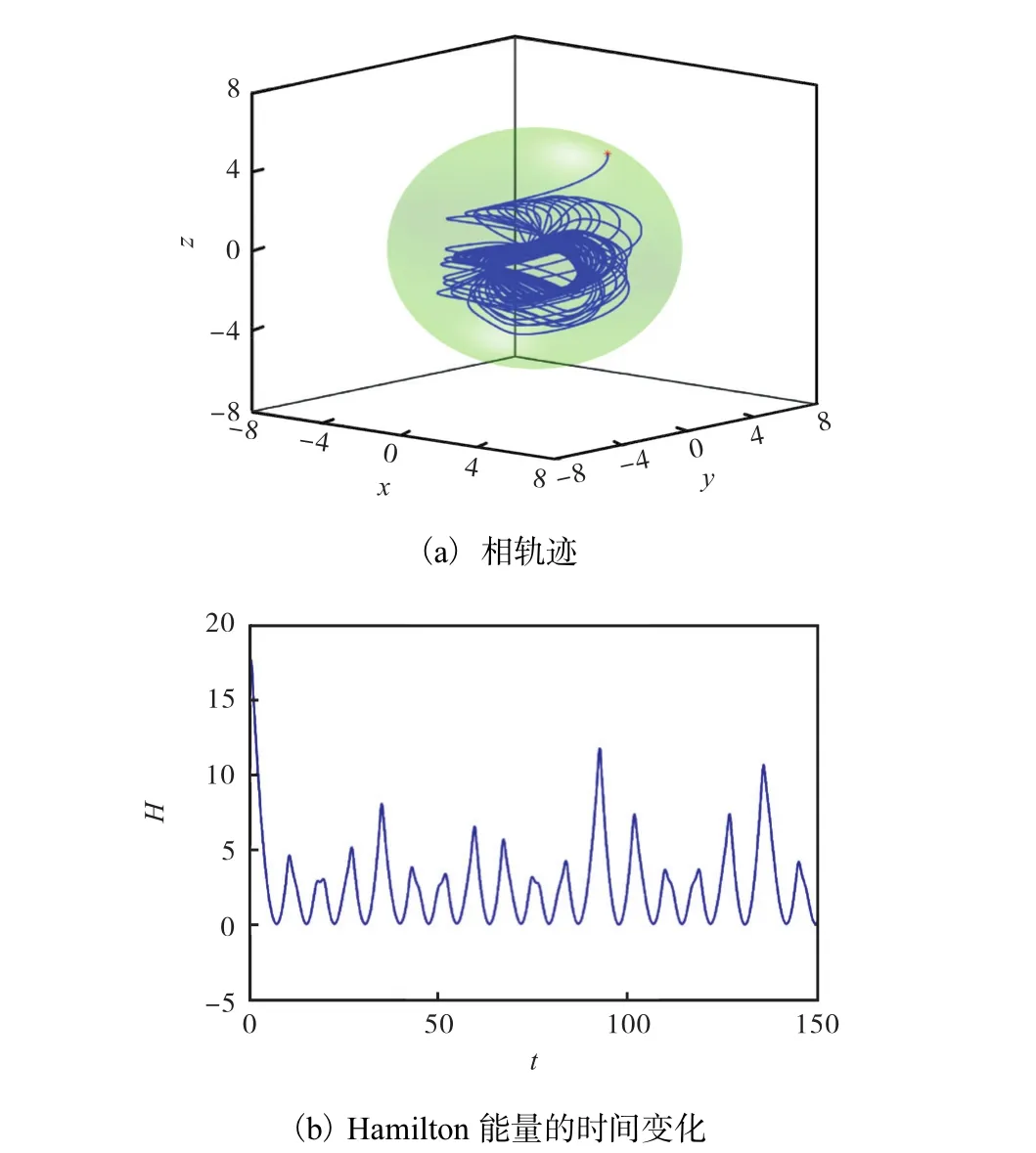
图4 系统(9)的动态特性Fig.4 Dynamic characteristics of the system(9)

金融系统受到扰动，系统中某些因素不按规则运行，但始终保持在有限的范围内，不会发散出去导致金融系统的崩溃.当市场经济发展迅速，货币流通量大时，国家为了防止通货膨胀的出现，可以通过提升利率x，汇集市场中流动资金的同时控制贷款总额，从而降低投资需求y，加快价格指数z的变化，同时二者的变化反作用于利率x，使其降低，从而三者间无规则往复变化，互相影响.

2.4 系统包含所有力矩

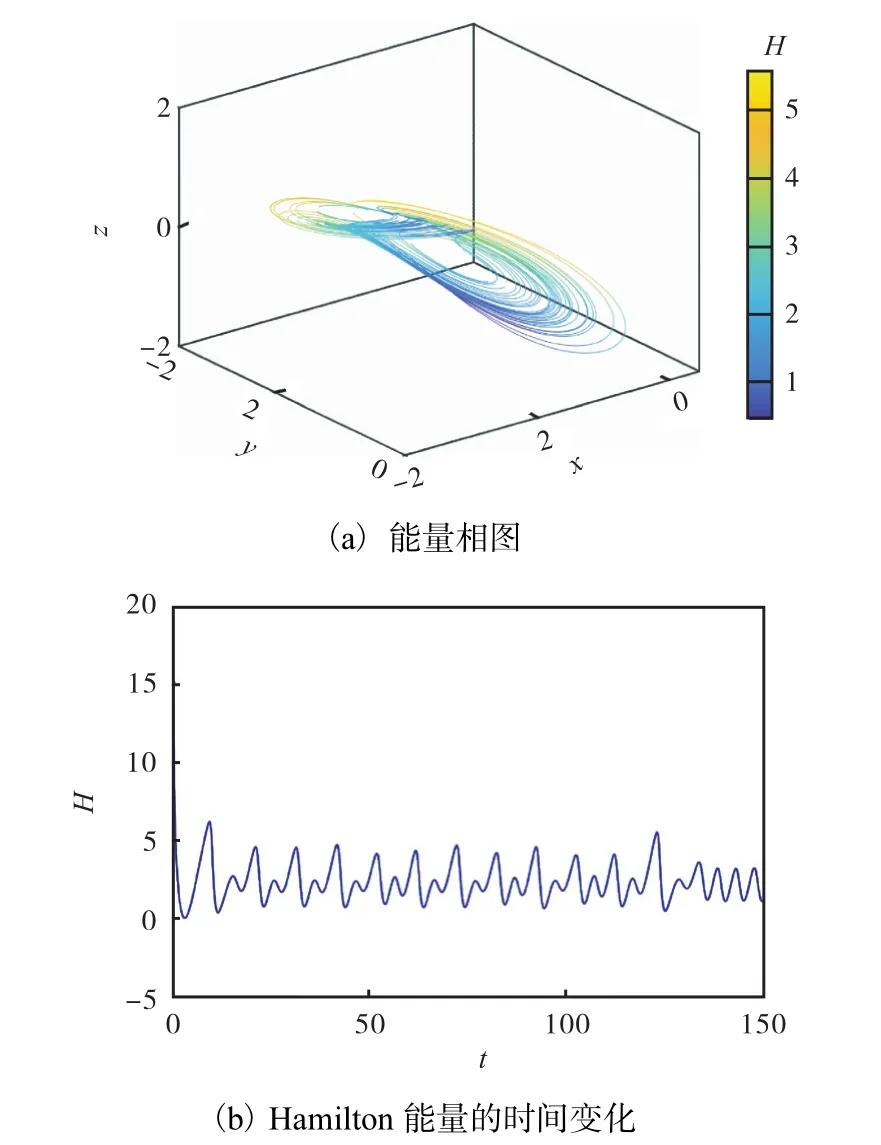
图5 系统(1)处于混沌状态时的能量Fig.5 Energy of the system(1)in chaotic state

比较 2.3节和 2.4节，这两种情况都会产生混沌行为，系统产生混沌振荡的唯一因素是外力矩f中的投资率 1.在 2.4节中，混沌的产生是外力矩 f与耗散力矩ΛX的相互作用的结果，在耗散力矩ΛX的作用下，系统各状态变量的振荡幅度减弱，系统的混沌行为得到一定程度的控制.2.4节比 2.3节加入了储蓄量a、单位投资成本b和商品需求弹性c.储蓄量a的大小直接影响利率x的变化，储蓄量a偏高时，央行会降低利率x，引导储蓄分流；当储蓄量a偏低时，央行会提高利率x，从市场汇集资金增加储备，二者呈反比关系.单位投资成本b的增加会降低投资需求y，单位投资成本b的降低会促使投资需求y的增多，呈反比关系.商品需求弹性c表示一定时期内商品需求量的变化对该商品价格的相对变动的反应程度，价格变动引起需求变动变化大，商品富有弹性(非必需品)；价格变动引起需求变动变化小或无变化，商品缺乏弹性(必需品)，呈反比关系.所以通过调节储蓄量a、单位投资成本b和商品需求弹性c的值可以对利率x、投资需求y和价格指数z的变化规律进行控制，从而有效控制金融系统的发展趋势.

3 基于有限时间LaSalle不变集的混沌控制

3.1 有限时间稳定理论

考虑非线性系统[17]

式中：x ∈ Rn为状态变量； f:D →Rn为定义域D到n维空间 Rn中的一个连续非线性函数.

定义 1[18]当且仅当系统(10)稳定，且在有限时间内收敛时，其平衡点x=0在连续有限时间内稳定，有限时间收敛可表示存在一个连续函数T(x):D0{0} → ( 0,+ ∞)使 ∀ x0∈ D0⊂ D.系 统(10)的解记作x(t,x0).

(1)当 t∈ [ 0,T(x0)]时 ，有 x(t,x0) ∈ D0{0}和x(t,x0) = 0 ；(2) 当 t＞ T(x0)时，有 x (t,x0) = 0.

当D=D0=Rn，系统的状态变量总能在有限时间内稳定到平衡点.

定理 1[19]设存在一个连续正定函数V(t)满足微分不等式

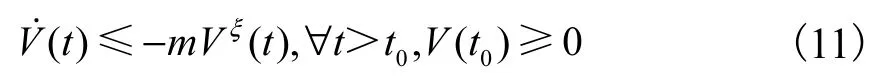
这里m和ξ为常数，且m＞0，0＜ξ＜1.对于任意初始时间t0，V(t)都满足不等式

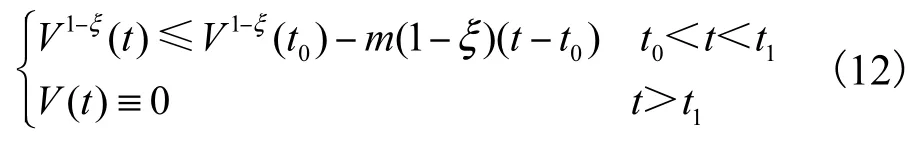
式中

文献[20]已对定理1进行了证明，此处不再赘述.

3.2 LaSalle不变集理论

考虑非线性系统

式中状态变量 X ∈Rn，f :D →Rn为定义域D到n维空间 Rn中的一个连续可微函数，满足 Lipschitz条件.设系统至少有一个平衡点 X*，且不知道该平衡点的位置.引入如下概念：

定义2f(x)在区域上满足Lipschitz条件时，应存在一个常数l使得定义域D中任意两个不同的实数x1和x2满足不等式.若f(x)在区域上D满足 Lipschitz条件，必定存在f(x)在区域D上满足一致连续.

定义 3设x(t)为系统(14)的解，存在时间t→+∞，使x(t) = Q ，则Q为x(t)的一个正向极限点.

定义 4设存在一个域 M ⊂Rn，若对任意初始条件x(0)=x0∈M ，系统(14)的解 x (t) = Φ(t,x0)满足x(t)∈M ，∀t≥0，则M 为系统(14)的正向不变集，可以包含系统的1个或多个平衡点，也可以是状态空间的一个子集合[21].

定理 2(LaSalle不变集定理[22])设Ω是一个有界闭集合，从Ω集合内出发的系统(14)的解x(t)⊂Ω，若∃V(x):Ω→R，具有一阶连续偏导，使dV/dt≤0，又设 A = {x|dV/dt= 0,x ∈ Ω}，M⊂A是最大不变集，则当t→+∞ 有x(t)→M ，若M={0}，则系统平衡点稳定.

3.3 金融系统有限时间LaSalle不变集控制

将系统(1)从平衡点 S1= ( 0,1/b, 0)转移到平衡点S0= ( 0,0,0)，并添加控制器u1,2得到受控金融系统的状态方程为

控制器u1,2的设计见式(16)，因金融系统中的利率x的变化受投资需求y以及价格指数z的影响，使得系统可能出现混沌行为，控制器的设计从削除影响利率因素的角度出发，利用控制器u1消除系统中的物价波动以及投资需求与利率的相互影响，并通过控制器u2增强利率的自身负相关性，以达到自身稳定的目的.

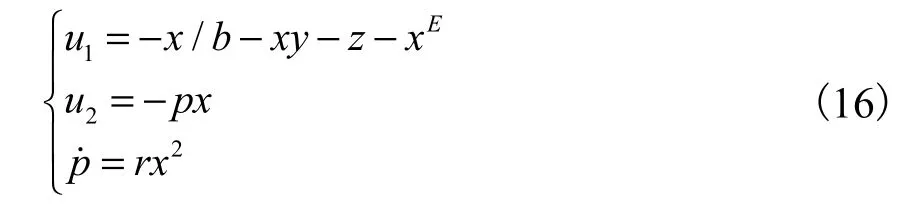
其中参数r＞0，指数E为真分数，p为状态变量.将式(16)代入状态方程(15)的第一项得到

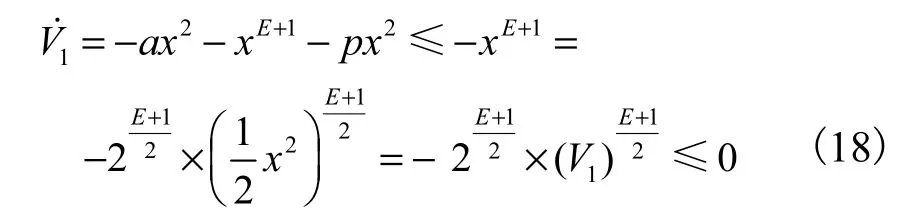
因为0＜E＜1，所以 0 ＜ ( E +1)/2＜1.根据定理 1可知，系统(17)能在有限时间 T1=/ (m1( 1 -ξ))内到达x=0处，其中ξ= ( E + 1 )/2.当 x=0时，=0且= 0 ，系统的状态变量x渐近稳定到x=0处.再将x= 0 代入系统(15)的后两项，并构造 Lyapunov函数V2= ( y2+ z2)/2，对其求导得到

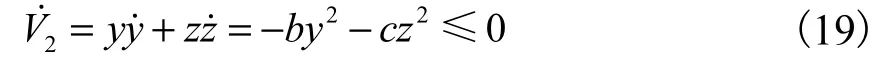
再令 g (x) = - a x - xE，则必定存在正实数l使，所以g(x)满足 Lipschitz条件，式(17)变换为

构造Lyapunov函数V3

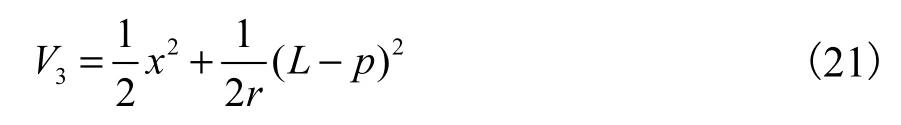
式中L为正实数，且L＞l，对V3沿着式的轨迹求时间微分，得到

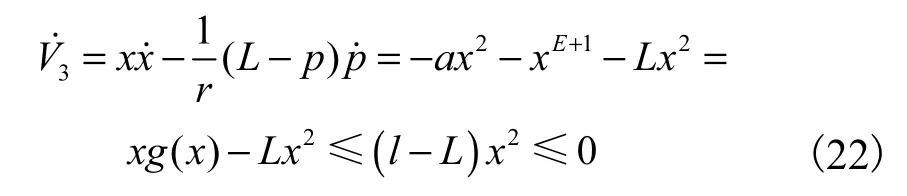
3.4 数值仿真

将控制器u1,2以及p加到系统(15)的第一项上，那么受控金融系统可表示为

当(a,b,c) = ( 1,0.2,1.1)、初始条件为I0时，系统(1)处于混沌状态.现保持系统(1)的参数和初始条件不变，采用四阶 Runge-Kutta法求解方程，设步长h= 0.001，状态变量 p0= 1 ，并选取控制参数E= 1 /2、r=1，对系统(1)的混沌行为进行控制.在第 60秒时加入控制器，状态变量x在控制器作用下迅速稳定，状态变量y、z随后很快全部稳定到平衡点，系统(1)的混沌振荡得到控制.图6给出受控系统(23)的3个状态变量的时间响应曲线，由此可以看出该控制方法可以将金融混沌系统的 3个状态变量从混沌状态控制到稳定状态.且状态变量的超调量几乎不存在，说明该控制方法的鲁棒性较强.

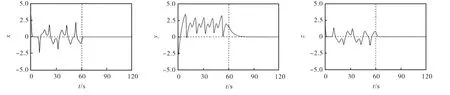
图6 受控系统(23)的时间响应曲线Fig.6 Time response curve of the controlled system(23)

注意，这里的控制器u1,2只作用于系统的x˙，也就是对利率变化的调节.在对原系统施加控制后，振荡的x在有限时间T1内被控制到稳定状态，稳定后的x可保证状态变量y和z的振荡随后同样得到有效控制.若要用控制器对y˙进行控制，只需先将y在有限时间内控制到稳定状态，从而带动x和z的收敛振荡，最终系统达到稳定平衡.同样的设计思路也适用于对z˙进行控制.

4 结 语

本文从两个方面研究了一种非线性金融系统.其一，从力学角度，将系统分解成 Kolmogorov系统形式，分析了不同力矩单独和共同作用于该金融系统时的结果，剖析了该金融系统产生混沌行为的原因，并结合金融市场解释了储蓄量和单位投资成本等因素间的作用关系.其二，将有限时间理论和 LaSalle不变集定理结合，设计了一种自适应控制器.该控制器结构简单、响应速度快且鲁棒性较强，只对利率的变化的调节就能将混沌的金融系统控制到稳定状态，为该金融系统的动力学研究提供了新的思路和参考.