含界面SiC/TC4复合材料拉伸强度预测及试验验证
2021-08-24沙云东
沙云东 周 颖 骆 丽
(沈阳航空航天大学 航空发动机学院,沈阳 110136)
高推重比航空发动机需要先进的材料和技术支持。复合材料的应用是增大航空发动机推重比的重要途径[1]。SiC/TC4复合材料具有高比强度、比刚度以及结构稳定性等特性,因此航空发动机涡轮轴和叶盘等部件的设计采用SiC/TC4复合材料已成为发展趋势[2-3]。对SiC/TC4复合材料进行力学性能预测,是复合材料结构设计的前提。界面在纤维与基体间传递载荷,因此将其纳入用于预测复合材料细观失效模型中十分必要。
通常复合材料的力学性能需要通过试验获取。Tan等[4-5]进行了复合材料拉伸试验,得到复合材料的纵向和横向拉伸强度、弹性模量和泊松比。但是,复合材料性能试验的成本较高,且试验结果存在分散性。近年来,通过有限元进行细观力学分析成为复合材料力学性能预测的有效方法。Gundel等[6]用数值分析确定了不同纤维排列形式下的界面应力,用同心圆柱模型得出复合材料弹性模量。Zahl等[7]计算了纤维排列和边界条件对连续纤维金属基复合材料横向强度的影响,得出45°加载时纤维按正方形排列比按六角形排列的强度高。Ever等[8]用代表体积元建立了高温条件下金属基复合材料强度预测模型,模型考虑了基体蠕变、界面开裂和界面粗糙度等影响因素。Lucas等[9]通过细观力学模型预测复合材料横向强度,根据试验修正Chamis模型的半经验公式,使得修正后的模型在横向强度预测方面取得了较大改进。Alireza等[10]利用麦克斯韦模型,提出了Mori-Tanaka粘弹性本构模型,以预测任意应变率下单向玻璃/环氧复合材料的刚性和强度。然而,通过含界面细观力学模型进行复合材料强度预测及其有效性验证的研究尚不充分,仍需进一步探讨。
本文基于双线性内聚力模型,建立含界面的SiC/TC4代表体积元模型,结合最大应力准则和最大位移准则,分析拉伸载荷作用下界面的损伤演化,预测SiC/TC4复合材料拉伸强度,并开展SiC/TC4层合板拉伸试验,对比预测强度与试验强度验证模型及计算方法的有效性。最后,在此基础上,讨论温度对SiC/TC4复合材料拉伸强度的影响。
1 理论方法
1.1 复合材料细观力学理论与强度理论
复合材料细观力学性能分析,是依托代表体积元模型(Representative Volume Element,RVE),根据纤维和基体的力学性能,获得单层复合材料力学性能的过程。在单向连续纤维增强金属基复合材料中,从横截面看真实纤维的分布是随机的,但具有统计均匀性。从细观结构来看,增强相在基体中的分布规律具有统计学上的均匀性,由此可分离出具有相同的弹性常数和纤维体积分数的代表性体积元。代表体积元可以由几个单胞或单胞的一部分构成。整个复合材料体可看作是代表体积元周期性排列而成[11]。以纤维和基体作为基本研究对象,根据纤维的排列方式、基体与纤维的力学性能及其相互作用等,建立四边形排列的复合材料代表体积元模型,如图1所示。

图1 四边形代表体积元模型
复合材料失效既是一个理论问题又是一个工程问题,因此失效准则的选取不仅要考虑合理性和准确性,还要考虑实用性。在三维失效破坏问题中,采用最大应力准则,对比材料各个应力分量和与之相对应的强度许可值。假如其中某一个应力分量值大于其对应的应力许可值,则材料在相对应的点上开始出现失效。最大应力准则具有应力分量以及应力分量之间简单独立和无相互作用的特点。对于复合材料结构破坏的三维失效问题,最大应力准则可以表示为:

式中:σ11、σ22和σ33为正向应力;τ12、τ23和τ13为切向应力;ei(i=1,…,6)为应力分量与各自失效强度的比值;下角标T表示拉伸,C表示压缩。
ei(i=1,…,6)与失效之间有如下关系:

1.2 界面模型理论研究
内聚力模型能够较好地分析界面应力,广泛应用于复合材料细观力学失效模式分析[12]。双线性内聚力模型本构关系如图2所示。其中:N为界面单元法向应力;Nmax为界面法向强度;δn为界面位移;斜率Kn为界面单元未出现损伤时的刚度;Dn为界面单元损伤指数。
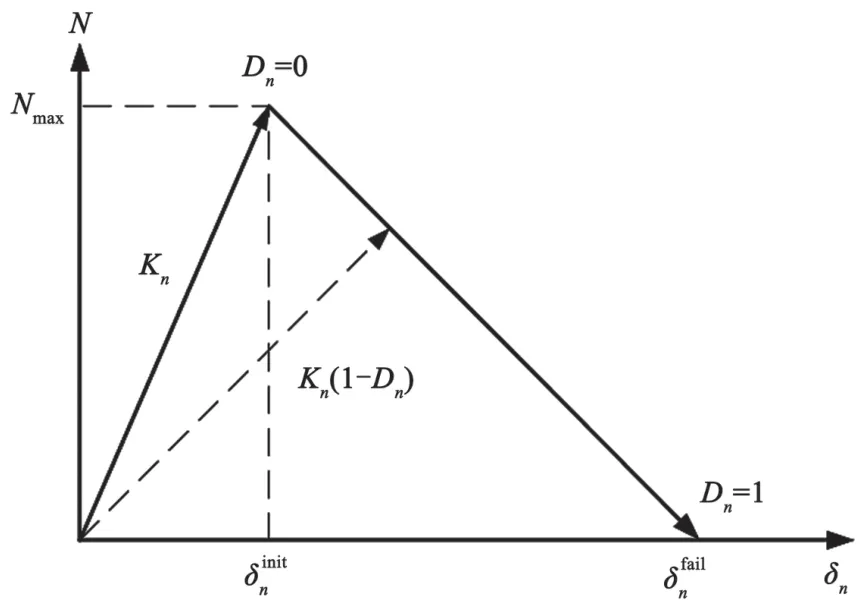
图2 界面单元本构关系
本文采用最大应力准则作为损伤起始判据,用最大位移准则作为损伤演化判据。最初阶段,随着界面位移的增加,裂纹尖端内聚力区域内应力在外载荷的作用下逐渐增加;在界面法向应力达到法向强度Nmax后,应力满足损伤起始判据即最大应力准则,该界面单元开始产生损伤,刚度出现衰退;此后,应力重新分配在损伤单元周围的界面单元上,已经出现损伤的界面单元承受的法向应力随位移的增加而减小,当位移达到最大失效位移时,损伤逐渐累计直到该界面单元损伤指数Dn为1,刚度衰退为0,失去承载能力。SiC/TC4复合材料中,界面层TiC的法向强度Nmax为98.5 MPa,最大失效位移为0.000 5 mm。
1.3 周期性边界条件
复合材料可假设为由RVE单元周期性排列得到,这就要求RVE模型中相邻单元的应力与位移都具有连续性,因此对RVE模型施加周期性边界条件更接近基本力学特征。研究表明,要使RVE模型同时具有应力连续性和位移连续性,需要对其施加周期性边界条件。因此,周期性边界条件应同时满足位移连续条件和应力连续条件[13-14]。四边形排列的RVE模型的二维几何表示如图3所示。
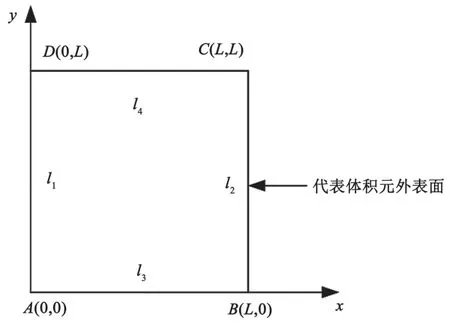
图3 四边形排列的RVE模型的二维几何表示
RVE模型的边长为L,坐标原点为点A,点B和点D分别在x轴和y轴上,则对应边的边界条件为:

式中:uA、uB、uD为顶点A、B、D的变形量;如果用l1、l2、l3、l4分别表示代表体积元中x=0、x=L、y=0、y=L时的边界,用uli表示代表体积元边界li上点的变形量,则式(3)和式(4)可写为:

RVE单元对应面上的应力大小相等、方向相反,从而保证应力场在相邻代表体积元之间是连续传递的;应力连续边界条件在周期性代表体积元施加位移连续边界条件时会同时成立[15]。
2 数值仿真与试验验证
2.1 模型建立
在计算单、双轴横向拉伸荷载的应力集中系数时,以SiC/TC4复合材料为研究对象,其中SiC为纤维材料,TC4为基体材料,界面层材料为TiC,纤维体含量为40%,性能参数如表1所示,其中E为材料弹性模量,μ为泊松比,XT为拉伸强度,XC为压缩强度。纤维直径100 μm,纤维体积分数为40%。四边形代表体积元模型边长为:

表1 SiC/TC4复合材料力学性能参数

式中:R为纤维半径;Vf为纤维体积分数。于是,计算可得建立的模型边长为140 μm。
针对代表体积元模型,首先应建角结点、棱边和面3种不同的结点集。其次,根据不同结点集的特征匹配结点,匹配结点时不能出现多余的结点,否则会造成错误的应力局部集中。为了方便结点匹配,通常需要保证代表体积元相对面上的结点数量和位置完全匹配。这需要对代表体积元模型划分周期性网格,从而将所有对应的角结点、棱边结点和面结点匹配成角结点对、棱边结点对和面结点对。最后,针对结点对,采用循环的方式,依次施加方程约束条件。根据以上步骤对四边形代表体积元模型编制周期性边界条件施加程序,完成周期性边界条件约束的施加。
2.2 计算结果与分析
根据表1对RVE模型赋予材料属性,并分别对纤维体积分数为40%的SiC/TC4复合材料RVE模型施加拉伸载荷,得到RVE模型在纵向拉伸载荷下的界面损伤云图如图4所示,在横向拉伸载荷下的界面损伤云图如图5所示。其中,σl为纵向拉伸载荷,σt为横向拉伸载荷。
图4为RVE模型中界面随着纵向拉伸荷载增大的损伤过程。图4(a)为100 MPa纵向拉伸荷载下界面的损伤情况,此时界面的损伤指数为0,界面内聚力单元处于线弹性阶段,位移随应力呈线性变化趋势,并未发生损伤。图4(b)为204 MPa 纵向拉伸荷载下界面的损伤情况,此时界面的两侧处开始出现衰退的现象,界面的最大损伤指数为0.010 3。由于最大损伤指数小于1,此时界面并未开裂。图4(c)为510 MPa纵向拉伸荷载下界面的损伤情况,此时界面衰退的区域扩大,衰退的程度加大,界面的最大损伤指数为0.627 4,界面仍未开裂。图4(d)为1 022 MPa纵向拉伸荷载下界面的损伤情况,此时纤维已到达失效强度,界面衰退的区域和衰退程度进一步加大,界面的最大损伤指数为0.827 8,界面仍未开裂。

图4 RVE模型在纵向拉伸载荷下的界面损伤云图
图5为RVE模型中界面随着横向拉伸荷载增大的损伤过程。图5(a)为10 MPa横向拉伸荷载下界面的损伤情况,此时界面的损伤指数为0,界面处于线弹性阶段,并未发生损伤。图5(b)为28 MPa横向拉伸荷载下界面的损伤情况,此时界面的两侧处开始出现衰退现象,但此时界面并未开裂。图5(c)为50 MPa横向拉伸荷载下界面的损伤情况,此时界面衰退的区域向两侧进一步扩展,衰退程度加大,界面的最大损伤指数为0.720 4,界面仍未开裂。图5(d)为71 MPa横向拉伸荷载下界面的损伤情况,此时界面的损伤指数已达到1,界面的两侧发生开裂。

图5 RVE模型在纵向拉伸载荷下的界面损伤云图
RVE模型各组成部分最大应力随拉伸载荷的变化规律及失效情况,如图6所示。

图6 纤维、基体与界面最大应力随拉伸载荷的变化规律
图6(a)为纤维、基体与界面最大应力随纵向拉伸载荷的变化规律。可以看出,随着纵向拉伸荷载的增大,代表体积元中各组成部分的最大应力都随之增大,其中纤维所受到的最大应力增长速度最大,表明纵向载荷作用下纤维为主要承力组分。纵向拉伸载荷大于1 022 MPa时,纤维所受的最大应力到达材料的极限强度,故纵向拉伸荷载下SiC/TC4复合材料的失效模式为纤维失效导致的复合材料失效。
图6(b)为纤维、基体与界面最大应力随横向拉伸载荷的变化规律。可以看出,随着横向拉伸荷载的增大,代表体积元中各组成部分的最大应力都随之增大,其中基体所受到的最大应力增长速度最大,表明横向载荷作用下基体为主要承力组分。横向拉伸载荷到达71 MPa时,界面发生开裂失效,此时界面应力达到结合强度失效。基体继续受力,当横向拉伸载荷大于447.4 MPa时,基体所受最大应力达到基体材料的极限强度,基体呈现拉伸失效现象。可见,纵向拉伸荷载下,SiC/TC4复合材料的失效模式为基体失效导致的复合材料失效。
2.3 试验验证
开展SiC/TC4层合板拉伸试验,对试验件施加拉伸荷载至断裂。SiC纤维直径为100 μm,纤维体积分数为40%。试验件长218 mm,宽24.5 mm,厚3.4 mm。
利用不同模型的强度预测结果与试验结果对比,如表2 所示。通过对比分析不同预测结果与试验数据可以发现:无论是对纵向拉伸强度的预测还是对横向拉伸强度的预测,利用含界面相同时施加周期性边界条件的RVE模型,计算都与试验结果有着更好的一致性。可见,所建立的纤维增强复合材料力学性能预测模型具有良好的合理性。

表2 利用不同模型的强度预测结果与试验结果对比
3 温度对SiC/TC4复合材料强度的影响
在不同温度场中对SiC/TC4复合材料施加纵向和横向载荷,得到纤维、基体与界面最大应力随纵向及横向载荷的变化规律分别如图7和图8所示。
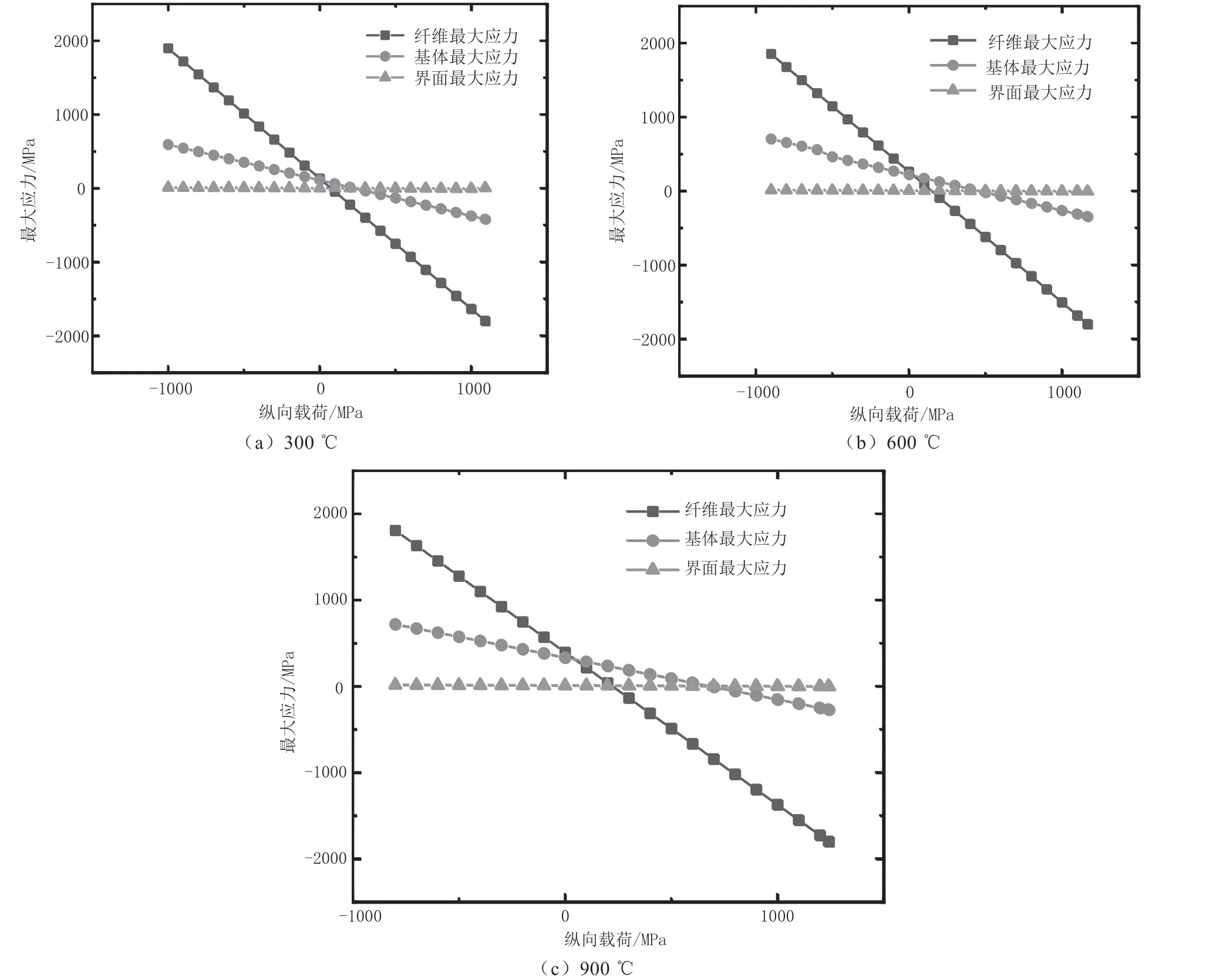
图7 不同温度场中纤维、基体与界面最大应力随纵向载荷的变化规律
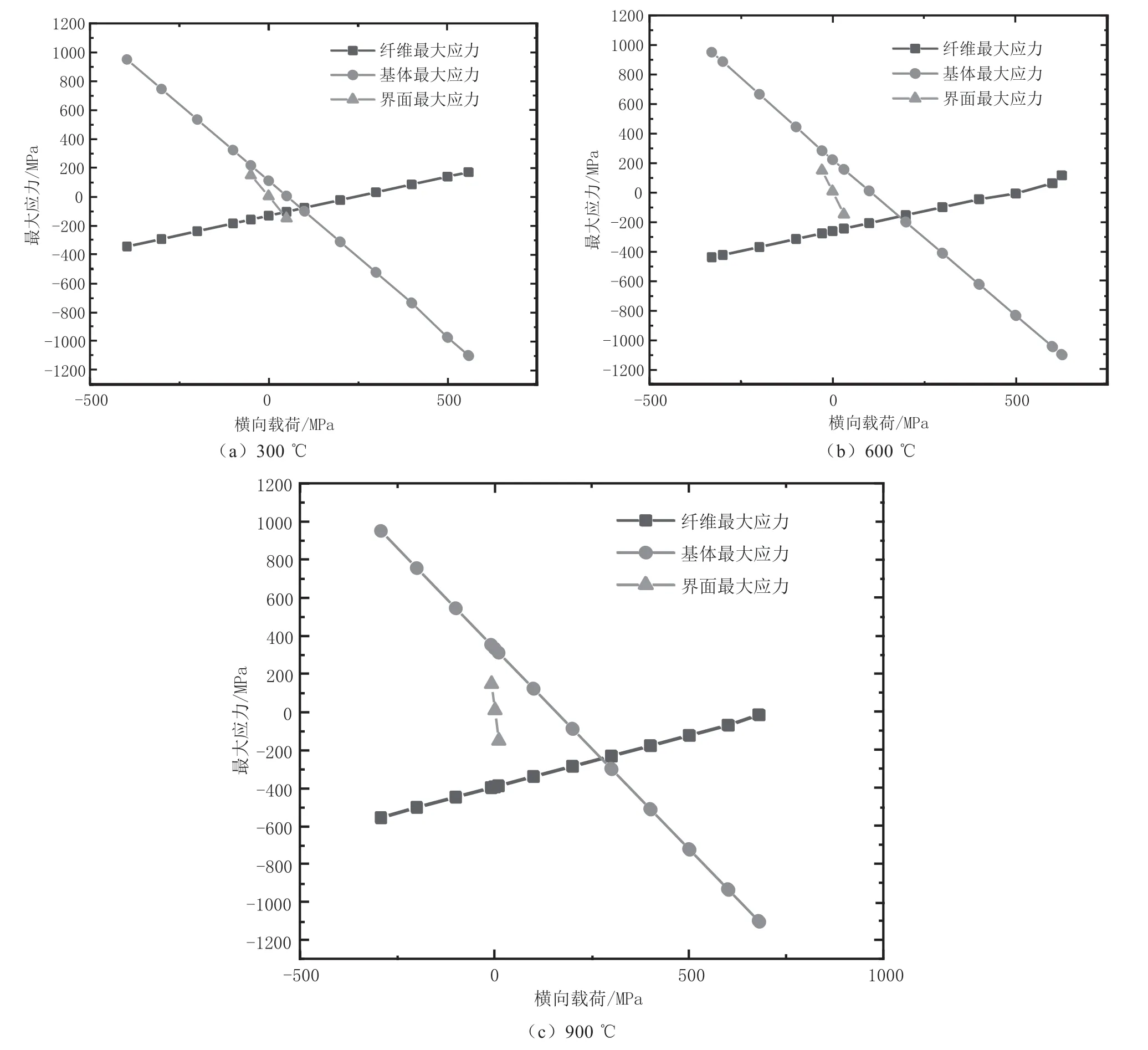
图8 不同温度场中纤维、基体与界面最大应力随横向载荷的变化规律
图7为不同温度场中纤维、基体与界面最大应力随纵向载荷的变化规律。横轴表示施加在代表体积元上的纵向载荷,负值表示纵向拉伸,正值表示纵向压缩;纵轴表示最大应力的值。从图7(a)可以看出,当温度为300 ℃时,纵向拉伸载荷大于955 MPa时,呈现纤维拉伸失效;纵向压缩载荷大于1 092 MPa时,呈现纤维压缩失效。从 图7(b)可以看出,当温度为600 ℃时,纵向拉伸载荷大于830 MPa时,呈现纤维拉伸失效;纵向压缩载荷大于 1 167 MPa时,呈现纤维压缩失效。从图7(c)可以看出,当温度为900 ℃时,纵向拉伸载荷大于796 MPa时,呈现纤维拉伸失效;纵向压缩载荷大于1 241 MPa时,呈现纤维压缩失效。可见,随着温度的升高,纵向拉伸失效强度减小,而纵向压缩失效强度增加。究其原因,在于SiC/TC4增强复合材料中基体的热膨胀系数大于纤维的热膨胀系数。复合材料受热后基体的形变量大于纤维的形变量,故温度升高会加速纵向拉伸失效,延缓纵向压缩失效。
图8为不同温度场中纤维、基体与界面最大应力随横向拉伸载荷的变化规律。横轴表示施加在代表体积元上的纵向载荷,负值表示横向拉伸,正值表示横向压缩;纵轴表示最大应力的值。从图8(a)可以看出,当温度为300 ℃ 时,横向拉伸载荷大于397 MPa时,呈现基体拉伸失效;横向压缩载荷大于559 MPa时,呈现基体压缩失效。从 图8(b)可以看出,当温度为600 ℃时,横向拉伸载荷大于330 MPa时,呈现基体拉伸失效;横向压缩载荷大于626 MPa时,呈现基体压缩失效。从图8(c)可以看出,当温度为900 ℃时,横向拉伸载荷大于292 MPa时,呈现基体拉伸失效;横向压缩载荷大于679 MPa时,呈现基体压缩失效。可见,随着温度的升高,横向拉伸失效强度减小,而横向压缩失效强度增加。究其原因,在于SiC/TC4增强复合材料中基体的热膨胀系数大于纤维的热膨胀系数。复合材料受热后基体的形变量大于纤维的形变量,故温度升高会加速横向拉伸失效,延缓横向压缩失效。
4 结语
含界面代表体积元模型模拟纤维体积分数为40%的SiC/TC4复合材料拉伸失效:纵向拉伸载荷下SiC/TC4复合材料的失效模式为纤维失效导致的复合材料失效,纵向拉伸强度为1 022 MPa;横向拉伸荷载下的失效模式为基体失效导致的复合材料失效,横向拉伸强度为447.4 MPa。开展SiC/TC4层合板拉伸试验,对比试验强度与预测强度,表明建立的纤维增强复合材料力学性能预测模型具有良好的合理性。在不同温度场中对SiC/TC4复合材料施加纵向和横向载荷,表明随着温度的升高,复合材料拉伸承载性能增加,压缩承载性能减小。
