基于应用场景特征描述的无人机基站飞行高度部署

谭诗翰，金凤林，顿聪颖

（陆军工程大学 指挥控制工程学院，江苏 南京210007）

0 引言

近些年，随着无线通信技术的广泛应用和用户需求的逐步增加，地面通信系统在一些特殊情况下的局限性日益凸显。与此同时，将无人机作为飞行基站，作为地面通信系统的补充，可以有效弥补地面通信系统在灵活性和覆盖范围上的不足，受到了广泛的关注[1]。未来，无人机基站的应用将可能是非常广泛的。例如，无人机基站在热点地区（如体育场、露天音乐会等）流量需求激增环境下，可以用于增强网络容量和覆盖范围；在基础设施受到损害的紧急情况（如自然灾害）下，无人机基站可以用于快速恢复通信；在一些建设完整的蜂窝网基础设施非常昂贵的边远地区，可以通过部署无人机，减少对信号塔和电缆的需要，降低网络建设成本。但是，无人机基站的部署也面临着许多难点。首先，无人机基站的可用带宽和机载能量有限，需要合理分配无人机基站的资源；此外，与地面网络系统不同，无人机基站可以在3D平面上灵活部署，在不同的应用场景下，需要根据实际情况，对无人机基站进行部署。

目前对无人机基站部署的相关研究工作集中于扩大无人机基站的服务覆盖范围。文献[2]导出了使单个无人机能够实现最大覆盖面积的最佳飞行高度。文献[3]在文献[2]的基础上，讨论了机载基站的定向天线波束宽度以及天线倾角对无人机覆盖范围的影响。文献[4]拓展到多个无人机基站的应用场景，得到了多个无人机基站服务覆盖范围最大的最优飞行高度。这些研究都以视距通信（Line-of-Sight，LoS）概率作为中介参数，以用户的接受信号强度阈值作为约束条件，忽视了无人机基站资源限制。一些研究将重点转移到用户需求层面上。文献[5]考虑到地面用户存在不同服务质量（Quality of Service，QoS）需求情况下，无人机基站覆盖用户量最多的3D部署。但是，文献[5]仅以接收信号强度作为用户QoS的唯一标准，限制了其应用范围。文献[6]讨论了无人机基站和终端直通（Device to Device，D2D）网络共存的情况下，无人机飞行高度与D2D网络服务质量之间的权衡关系，得到了区域内吞吐量最大情况下的D2D用户密度以及无人机飞行高度。文献[7]从 体 验 质 量（Quality of Experience，QoE）的 观 点出发，得到了能量效率最高、吞吐量最大的无人机基站部署方案。文献[7]主要解决的是动态无人机基站问题。此外，文献[8]和文献[9]针对无人机基站的最短时延问题进行了讨论，文献[10]和文献[11]针对无人机基站在空天地一体化网络中的应用进行了讨论。

实际上，无人机基站的部署需要根据应用场景的不同进行相应的调整。例如，无人机基站在应对一些突发流量和区域热点的情况下，用户分布集中，传输速率需求大，可以通过下调飞行高度来满足服务用户的传输速率；而在应对边远地区或者灾害临时服务的场景下，用户分布广，可以通过上调无人机基站的飞行高度来扩大无人机基站的服务覆盖范围。因此，需要针对不同的应用场景，调整无人机基站部署。然而，现阶段研究经常忽视这个问题。

本文针对无人机基站应用场景不同，将无人机基站应用场景抽象为四个方面特征：（1）地理环境；（2）用户分布；（3）用户需求；（4）优化目标。具体分析了两种典型的无人机应用场景，根据应用场景特征描述，获得不同应用场景下无人机基站最优飞行高度的数学模型。

1 信道模型

考虑如图1所示的场景模型。无人机悬停高度为h，在地面上的投影点为O，假设地面用户u距离点O的距离为ru，则无人机和用户u的距离为：

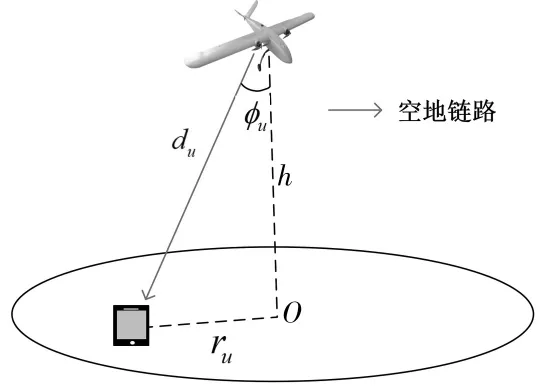
图1 空地链路模型

无人机-用户垂直方向上的倾角为：

无人机携带定向天线，天线方向与水平面垂直，并且无人机天线水平半功率波束宽度和垂直半功率波束宽度相同，表示为b。假设系统内不存在其他 网 络 系 统 对 空 地 链 路 的 干 扰 。 Su，LoS（t）和 Su，NLoS（t）分别为t时刻LoS和NLoS条件下用户u的接收信号强度，表示为：

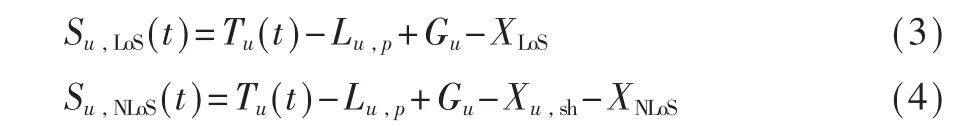
其中Tu（t）为t时刻无人机基站的发射信号强度，Lu，p为信号自由路径损耗，Gu为定向天线在瞄准角处的最大增益，Xu，sh为 NLoS阴影衰落。在 NLoS场景中，由于障碍物的存在，影响到电磁波的传播，阴影衰落是一种只与 NLoS场景相关的现象[12]。Xu，sh服从正 态分布 N（μu，sh，σu，sh）。XLoS和 XNLoS分 别 表 示 在 LoS和NLoS条件下，真实环境下的随机因素，分别服从正态分布 N（0，σLoS）和 N（0，σNLoS）。 通过计算可以得到：

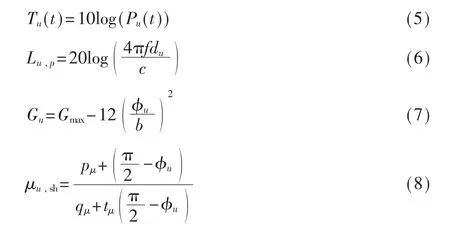
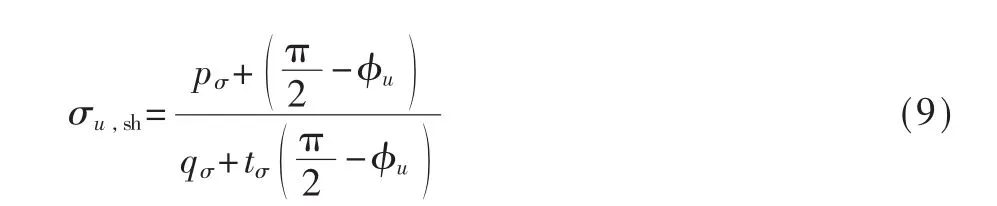
式中 Pu为天线的发射功率，f为频率，c为光速，pμ、qμ、tμ、pσ、qσ、tσ为 不 同 频 率 下 的 经 验 值[10]。 本 文 采 用了国际电信联盟（ITU）推荐的空地信道模型，具体经验参数值见表1。

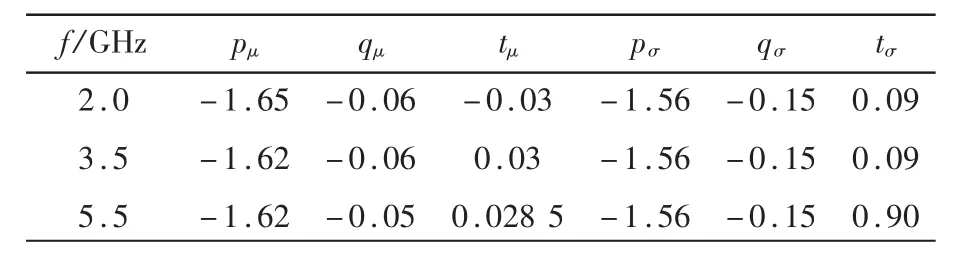
表1 不同频率阴影衰落参数值

Gmax为最大天线增益[13]，近似为：

空地链路为LoS和NLoS的概率分别为：

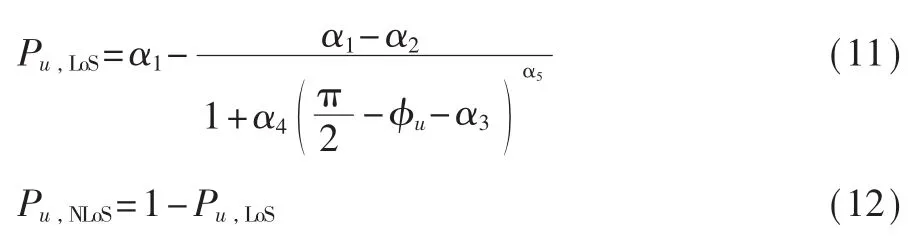
其中 αv，v∈{1，2，3，4，5}为经验参数，其值与用户所处的地理环境有关。文献[13]、[14]中区分市区和郊区环境构建传输信道模型，并进行了大量参数的验证，具体参数值见表2。

表2 不同环境LoS和NLoS概率参数

本文采用用户接收信号强度的均值表示t时刻用户u的接收信号强度Su（t）：

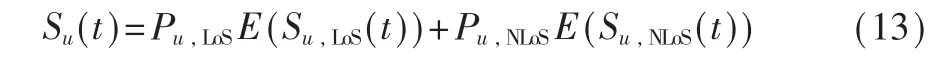
其 中 ，E（Su，LoS（t））=Tu（t）-Lu，p+Gu，E（Su，NLoS（t））=Tu（t）-Lu，p+Gu-μu，sh。

2 应用场景模型

考虑如图2所示的无人机基站应用场景模型。无人机基站的总功率为P，总带宽为 B。场景a和场景b分布代表两种不同类型的无人机基站应用场景。其中，场景a对应于一些热点地区数据量激增情况下的无人机基站辅助通信场景，这些场景的用户分布区域有限，但是用户密度高，用户对传输速率和时延要求较高，提高无人机基站对用户的数据传输速率可以提高用户服务体验；场景b对应于无人机基站用于灾后的临时通信或者边远地区的通信，这些场景一般用户分布范围较大，用户密度小，用户对传输速率和传输时延要求较低，但是需要无人机基站有尽可能大的覆盖范围，服务更多用户。因此，场景a和场景b的特征描述为：

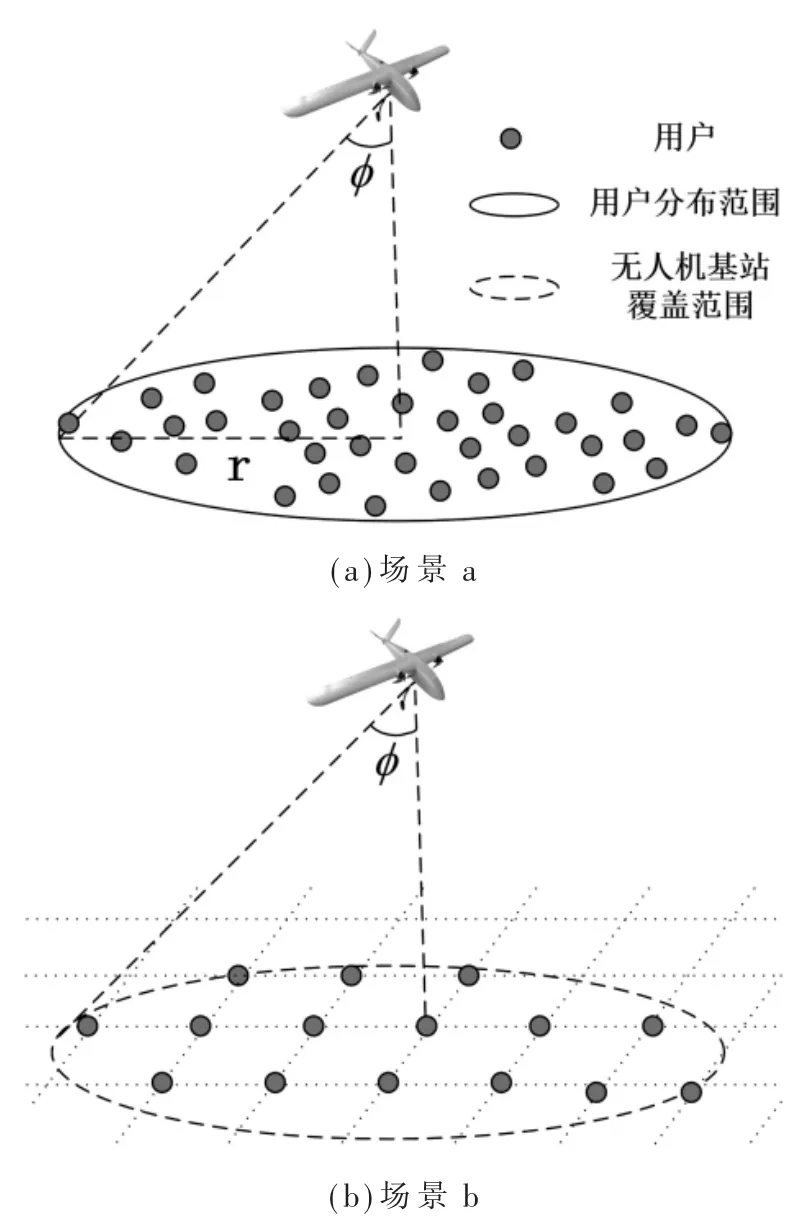
图2 无人机基站应用场景

（1）地理环境：场景a对应实际应用场景一般发生在城市环境，场景b对应的实际应用场景一般发生在郊区。

（2）用户分布：场景a中用户分布于有限的圆形区域范围内，区域半径为 ra，用户数量为 na；场景 b中用户分布范围不限，用户密度为 ρb，假设用户均匀分布，无人机基站在场景b中的服务范围为半径为rb的圆形区域，无人机基站服务用户数为：

（3）用户需求：本文中用户需求由最小传输速率和最大时延表示。假设同一场景内的用户需求相同，场景a和场景b内用户的最小传输速率和最大时 延分别为 ：wa、τa和 wb、τb。

（4）优化目标：在无人机基站满足所覆盖的用户最低服务需求的前提下，本文为场景a和场景b中无人机部署设置了不同的优化目标。场景a为最大化无人机基站对用户的最小传输速率，场景b为最大化无人机基站的覆盖面积。

3 最优飞行高度

分析无人机基站的最优分析高度，首先要满足无人机基站覆盖用户的通信需求。用户需求一般由多维参数组成，包括中断概率、接收信号强度、信号抖动、最小传输速率和最大时延等。本文仅考虑用户的最小传输速率和最大时延。无人机基站对用户的传输速率低于用户最小传输速率则认为是链路中断。本文中的时延是指用户连接时延。在现实世界中，不同的用户有不同的数据速率要求。根据用户对传输速率需求的不同，用户分为实时用户或非实时用户（比如直播、常规视频播放等）[15]。 实时用户对延迟有极高的要求，而非实时用户对延迟要求很低或没有。本文假设低传输速率需求的用户是非实时用户。

t时刻，无人机基站到用户u传输速率计算为：

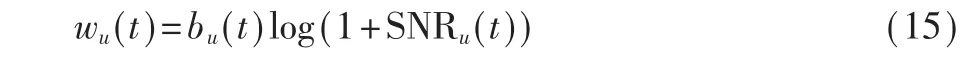
其中，bu（t）为t时刻无人机基站分配给用户u的带宽，SNRu（t）为t时刻用户u接收信号的信噪比，计算为：

其中，N为噪声强度。

假设无人机基站对用户的访问周期为T，并且保证在单个访问周期内，用户至少获得一个时隙的传输服务，则用户 u的时延 τu≤T。 由于：

因此：

以下区分场景a和场景b对无人机基站的最优飞行高度进行讨论。具体模型参数设置如表3所示。

表3 模型参数设置

3.1 应用场景a

3.1.1 问题描述

根据场景a的特征描述，将场景a的无人机基站最优飞行高度问题描述为：

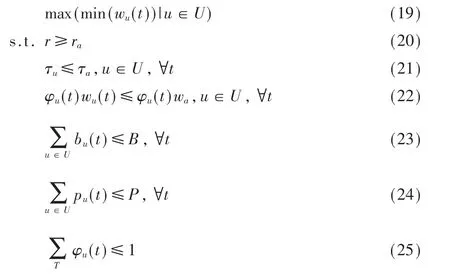
其中，U 表示区域内用户的集合，φu（t）∈{0，1}，如果在t时刻为用户 u提供服务，则 φu（t）=1，否则 φu（t）=0。式（20）为无人机最小覆盖范围的限制，式（21）表示用户的最小传输需求，式（23）、式（24）表示无人机基站资源限制，式（25）表示一个周期T内用户至少获得一个时隙的传输服务。

3.1.2 分析计算

假设无人机基站向每一个用户分配相同的带宽和发射功率，则用户u在t时刻的带宽和发射功率为：

式中，n（t）为t时刻无人机基站服务的用户数。

由式（26）、式（27）可知，u在 t时刻的带宽和发射功率与用户数量成反比。可以通过最小化n（t），使用户获得最大的带宽和发射功率。令无人机基站对单个用户在一个访问周期T内访问一次，则：

假设无人机基站可以合理安排用户的访问时隙，t时刻无人机基站服务的用户数的最小值为：

由式（13）可知，在无人机基站飞行高度h一定的前提下，用户传输速率与ru成反比，所以区域边缘的用户传输速率最低，对区域内用户最小传输速率的计算，实际上是对区域边缘用户传输速率的计算，所以令：

将式（1）（2）（13）（16）（30）代入式（15），可以得到区域内用户最小传输速率和无人机基站飞行高度h的函数，如式（31）所示。

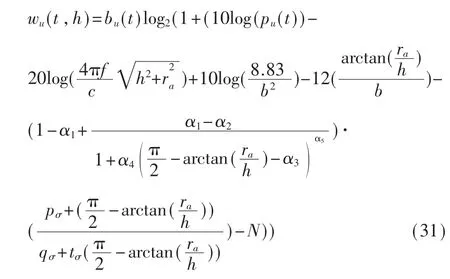
将式（26）和式（27）代入式（31），并对式（31）求导，获得式（31）的导数图，如图3所示。假设无人机基站的飞行范围在区间（1 000，15 000）之间[10]，可以看出，用户最小传输速率 wu（t，h）为凸函数，并且在无人机基站的飞行范围内存在极值点，即最大值点，求解：

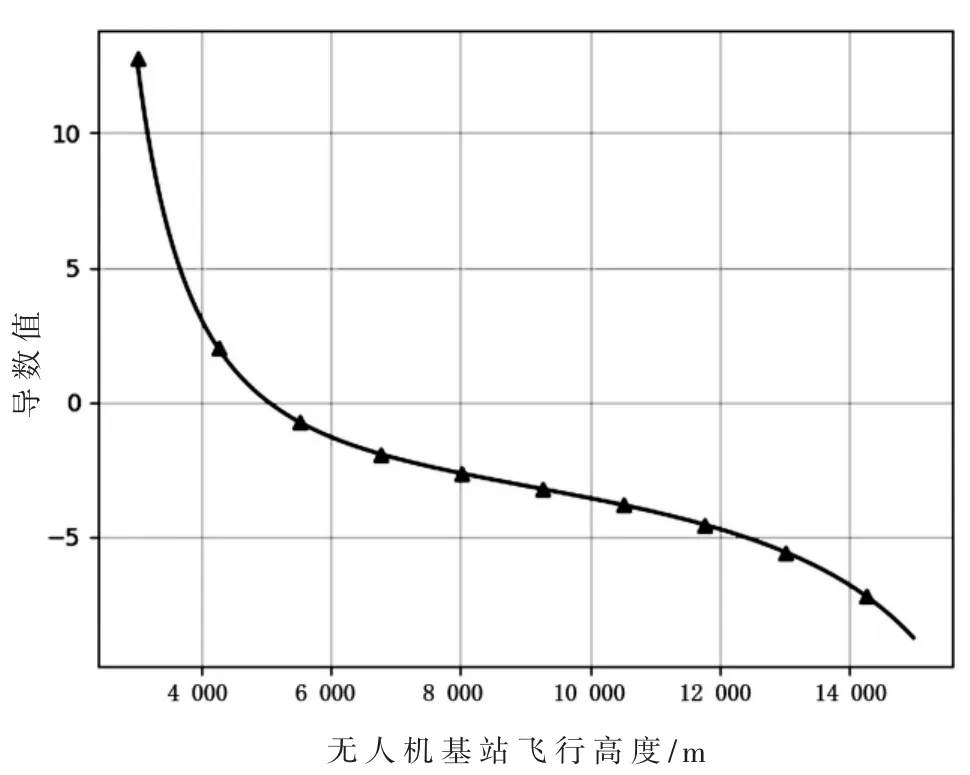
图3 wu（t，h）的导函数图像

获得最大值点无人机的飞行高度值。由于式（32）为高阶函数，没有显示表达的求根公式，本文通过一元函数牛顿法，近似求解。

3.1.3 实验结果

如图4所示，区域范围一定的情况下，相同的用户数量，在无人机的飞行高度区间（1 000，15 000），存在一个最优的无人机基站飞行高度，使用户最小传输速率最大，图中虚线表示不同用户数量下无人机最优飞行高度的连线。同时可以看出，在相同的基站飞行高度下，用户数量越多，用户最小传输速率越小。这是由于区域内用户数量越多，无人机基站给单个用户分配的传输功率和带宽资源越少。但是，根据式（13）可知，无人机基站和用户之间的 LoS概率，以及阴影衰落和天线增益仅与无人机-用户垂直方向上倾角φu有关，与区域内用户数量无关。根据式（2），na和 φu不存在联系，用户数量与无人机最优飞行高度无关，所以不同用户数量下无人机最优飞行高度不变。

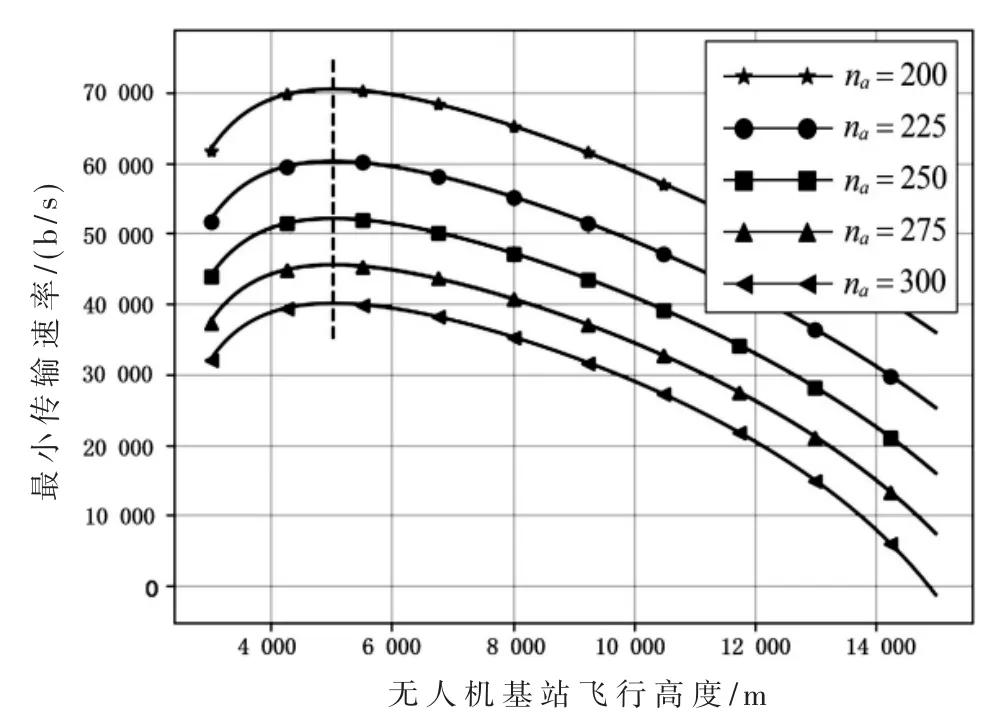
图4 不同用户数量无人机基站的飞行高度和最小传输速率关系

从图5中可以看出，随着区域范围的增加，在相同的无人机基站飞行高度下，用户的最小传输速率会减小。从上文的分析中可知，区域的覆盖半径ra与φu和无人机与用户距离d成正比，在 h不变的情况下，区域ra半径增加，则会增加信号的传输路径损耗，减少天线增益，减少LoS概率并增加阴影衰落，最终导致信噪比减少，用户传输速率下降。无人机基站飞行高度最优h与用户传输速率有着非常复杂的联系。从实验结果可以看出，随着区域范围的增加，无人机基站最优飞行高度也会增加。

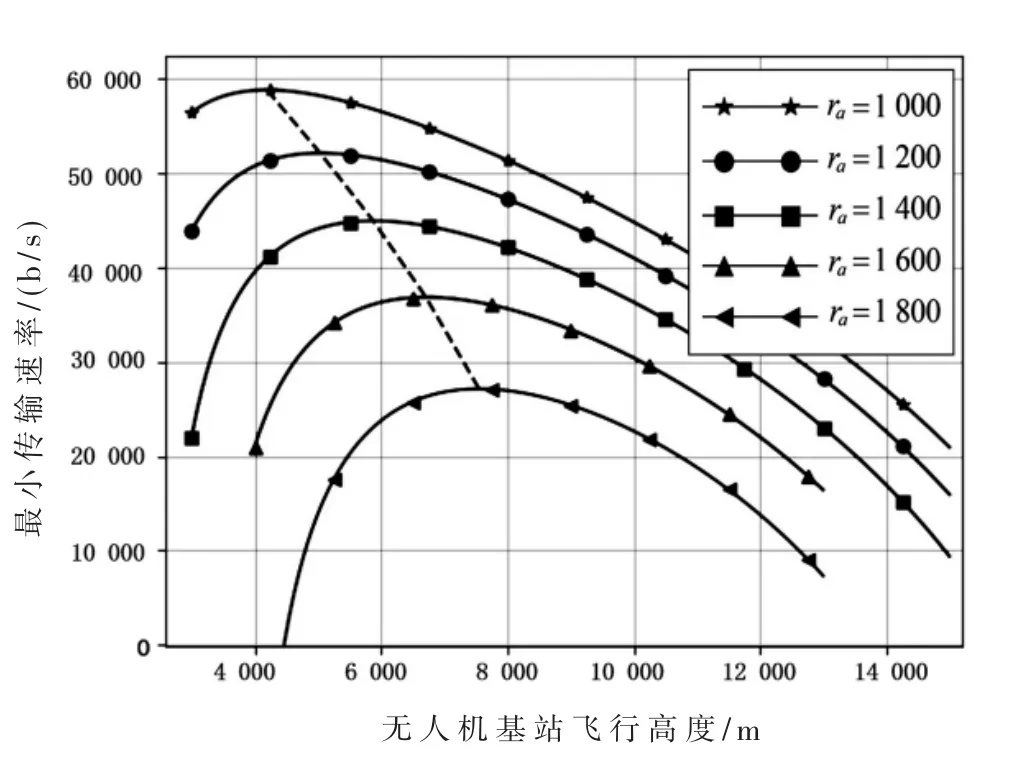
图5 不同区域面积无人机基站的飞行高度和最小传输速率关系

3.2 应用场景b

3.2.1 问题描述

根据场景b的特征描述，将场景b的无人机基站最优飞行高度问题描述为：

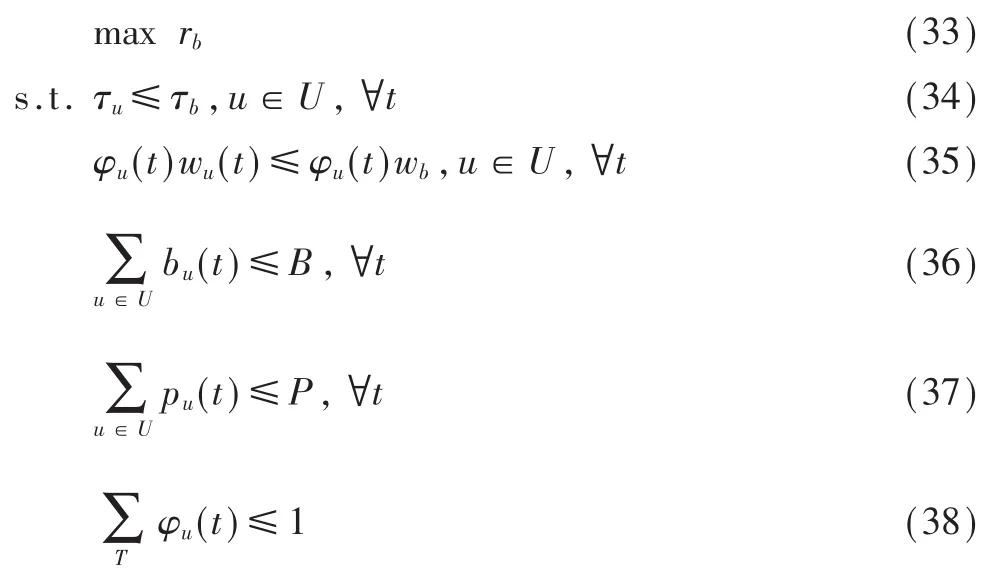
式（34）和式（35）表示用户的最小传输需求，式（36）和式（37）表示无人机基站资源限制，式（38）表示一个周期T内用户至少获得一个时隙的传输服务。

3.2.2 分析计算

无人机基站覆盖的用户数量随无人机基站的覆盖范围的增加而增加。根据第2节对场景b用户分布的假设，无人机基站覆盖的用户数量表示为：

同上一小节对场景a的讨论，t时刻无人机基站服务的用户数的最小值为：

用户在t时刻的带宽和发射功率为：

同场景a对区域边缘用户的传输速率进行分析，由于用户传输速率与ru成反比，因此当无人机基站飞行高度h一定时，区域边缘用户传输速率最小，则无人机覆盖面积最大。令wu（t）=wb，获得无人机基站覆盖区域半径rb和无人机基站飞行高度h的隐函数，如式（43）所示：

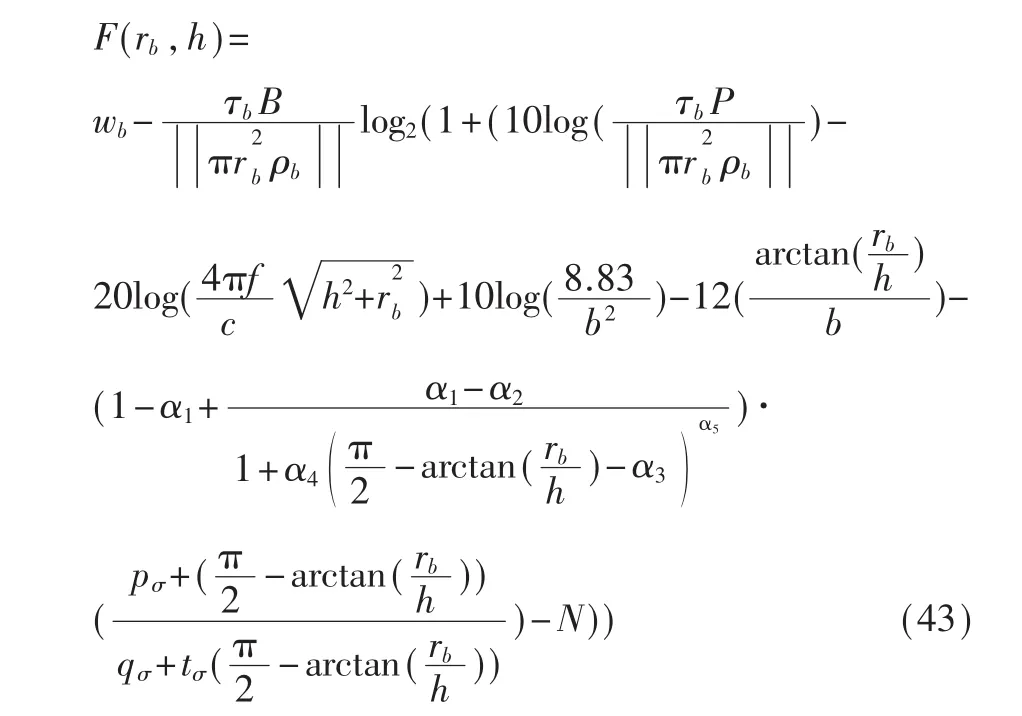
对式（43）求导，导函数图像如图6所示，可以看出，在 h∈[1 500，30 000]范 围 内[10]，导函 数存 在 唯一零点，即最大值点，求解：

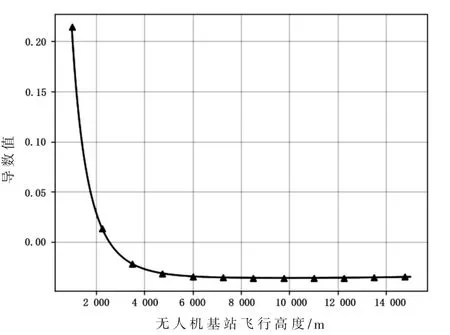
图6 无人机基站覆盖区域半径rb和无人机基站飞行高度h的导函数图像

获得h关于rb函数的极值点。

3.2.3 实验结果

如图 7所示，相同的区域用户密度ρb，在无人机的飞行高度区间（1 000，15 000），存在一个最优的无人机基站飞行高度，使无人机基站的覆盖面积最大，图中虚线表示不同用户密度下无人机最优飞行高度的连线。可以看出，在相同的无人机飞行高度下，区域用户密度ρb上升，无人机基站的覆盖面积下降。主要原因是随着ρb上升，相同覆盖面积下无人机服务的用户数增加，单个用户所能分配的信道资源和传输功率减少，使得区域边缘用户的最小传输速率难以满足用户需求，缩减了无人机基站所能覆盖的区域范围。同时，从图7可以看出随着区域用户密度ρb上升，无人机的最优飞行高度有所下降。

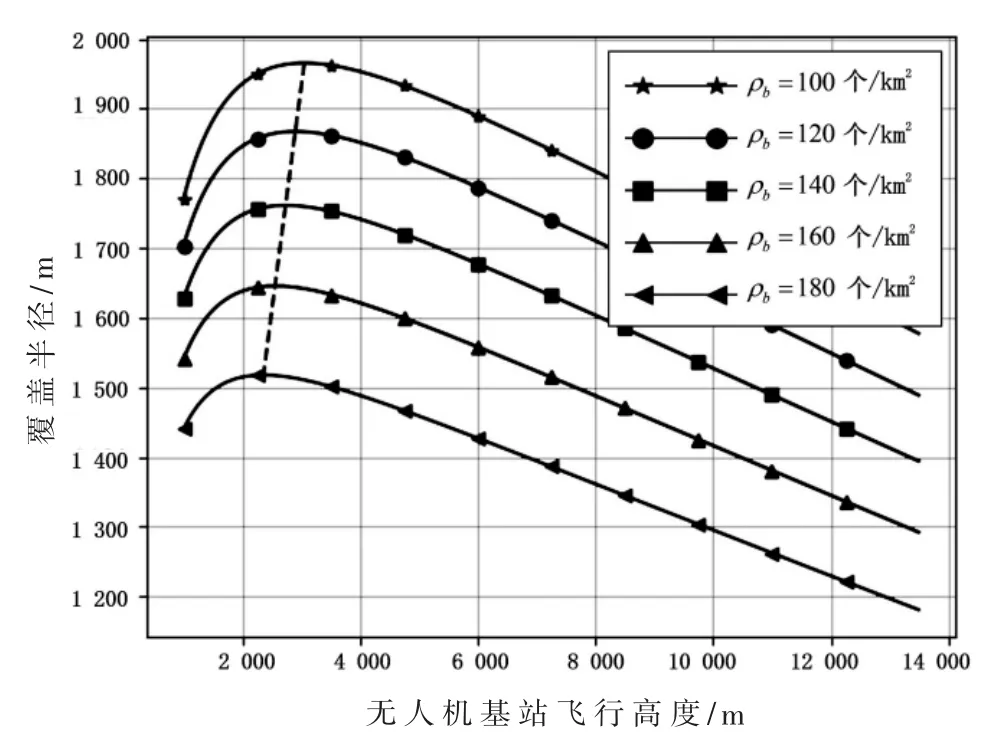
图7 不同用户密度无人机飞行高度和覆盖区域半径的关系

4 结论

本文从无人机基站在不同场景下的场景特征入手，针对两个不同典型的无人机基站应用场景模型，给出了最大化用户最小传输速率和最大化无人机基站覆盖面积的计算模型，找到了无人机基站的最优飞行高度。下一步工作的重点是对场景特征模型进一步细化，以及对多个无人机之间的协同做出更深一步的研究。