基于Flink流处理框架的FFT并行及优化*

钟旭阳 ，徐 云

（1.中国科学技术大学 计算机科学与技术学院，安徽 合肥230026；2.安徽省高性能计算重点实验室，安徽 合肥230026）

0 引言

快速傅里叶变换（Fast Fourier Transform，FFT）是实现离散傅里叶变换及其逆变换的算法。FFT使用分而治之的主要思想，其主要目的是将一个复杂的大问题分解成多个简单的小问题，然后分别解决这些小问题[1]。FFT在科学计算领域具有极其重要的地位[2]。利用FFT能够在计算离散傅里叶变换时大大减少所需要的乘法次数，并且FFT点数规模越大，FFT算法所能够节省的计算量就越显著，因此FFT广泛应用于数据信号处理、地震预报、石油勘探等领域。

已有的FFT分布式计算方法大多基于MapReduce批处理系统[1，3-5]，其中 FFT计算作为一个整体，在某一个转换操作中直接计算来自上一个操作的整个输出数据，忽视了FFT计算特性的同时，还需要等待较长时间才能延迟得到处理结果。目前并未有成熟的、基于流粒度的对FFT的流处理分布式算法并行优化相关研究。且现如今Flink分布式流处理框架大都用于社交网络等领域中简单的数据项统计应用，对于FFT此类耗时大、数据量大的科学计算问题并不适用，因此需要对Flink相关的机制进行应用和改造，使得其符合FFT计算的要求。

在Flink流处理框架中设计实现良好的FFT算法并行化流程及优化，不仅可以将FFT计算中的源数据流的特征表现得非常突出，推动了FFT计算在高精度、大宽带和实时性的要求上更进一步；而且为传统科学计算任务在大数据时代背景下，提供了一种基于分布式流处理平台的并行流程新思路。

1 相关研究

1.1 单机FFT算法优化现状

目前在单机上进行FFT并行设计、提高FFT计算速度的方法主要有两类。

一类主要优化FFT算法本身。1995年Varkonyi-Koczy[6]提出了新的递归FFT算法，力图提高处理时间。在生物医学方面，Brünger[7]等人提出了基于覆盖晶体晶胞的子网格的FFT变种算法，尝试使用自网格减少计算的内存消耗。郭金鑫[8]等人重构蝶形网络，在ARMV8及X86-64架构上构建了一个高性能FFT算法库。FFT高性能程序库、基于C的 FFTW[9]，通过高度优化的多线程代码和缓冲区优化等手段，成为目前行业内顶尖的单机并行FFT程序库。与此类似的包括基于GPU的cuFFT[10]和基于Java的Jtransform[11]等。

另一类主要在集中式的硬件平台上进行并行化优化。例如文献[12]将多块DSP芯片集成在一片信号处理器中，辅以多种硬件加速器，对一个FFT输入数据进行计算。文献[13]采用DSP芯片实现高速信号采集和FFT的实时运算。这种平台已有成熟的产品，例如TMS320C6678多核DSP公司的雷达信号处理系统等。

但是由于单机的资源有限，单机和集中式环境扩展性不高，前端传感器输入数据量大、数据速率快，虽然已经有相当多的对FFT算法本身和对单机并行FFT程序库的优化研究，但是处理大规模数据仍然效率不高，且无法充分发挥集群机器CPU和内存资源在解决此类大规模问题上的优势[14]。因此使用大数据分布式框架成为目前FFT并行处理的重要手段。

1.2 分布式FFT算法并行流程及优化现状

目前已有很多在分布式框架上搭建FFT应用的研究工作。Duc[3]在 Hadoop和 Spark系统上设计了一种可扩展的FFT计算系统，以提供给声学进行分析和使用。王菊[15]等人基于MapReduce改进了FFT算法，设计不同的组件按顺序提交数据补零、变址运算、蝶式计算、格式化四个阶段，使得以时间为基准的基-2 FFT算法能在框架上并行执行，并应用于风电机组的发电场景上。赵鑫[16]等人设计了一种非递归的增量式FFT方法，在计算过程中加入队列结构缓冲数据以解决数据传输过程中丢失和乱序问题，并应用于转子合成轴心轨迹监测中。

但目前FFT分布式设计大多本质都是批量处理，要求先存储后计算，这种方法一方面有较多的时间花费在IO读写上，需要对大批量的数据进行存储复制，另一方面无法实现实时的数据处理，数据延迟高。

由于单机环境和分布式环境有本质区别，单机FFT算法并未考虑其在分布式环境下的多机并行等问题。本文根据 FFT算法本身的特点，设计了FFT在流式引擎Flink中的并行流程。将每帧数据并行拆分，在多级并行实例间构建蝶式变换，随后逐级合并，同时在多帧数据间实现流水线计算。本文设计了蝶式计算递归深度的自动调优，以自动设置在不同点数、不同集群中的最优深度，将计算时间降至最低。另外，本文对Flink原有窗口进行了改造，实现以数据空间信息为触发条件的窗口机制，使得蝶式计算数据全部到达时触发窗口计算。同时在窗口内设计了多帧缓冲队列，以防出现位置覆盖、乱序、计算错误等问题。

2 方法设计

2.1 FFT流处理并行流程设计及优化

本文参考了1965年Cooley和Tukey提出的经典递归基 2-FFT算法[17]，将其稍加改造，使得其适用于分布式流处理场景。

本文提出的基于Flink的FFT并行算法整体流程如图1所示。该并行流程主要分为四个部分，分别为蝶式计算数据划分、位置窗口触发计算、小数据块FFT计算和蝶式计算多级合并。

图1 FFT并行算法整体流程图

FFT数据的输入流实质为每帧雷达数据中的每个点。蝶式计算数据划分时，根据下游计算并行实例个数，将数据流按在整帧中的位置信息分发到对应的计算并行实例中，映射关系示例图如图2所示。某个位置的数据与计算并行实例编号的对应关系在初始化时计算并存于映射表中，在运行中可以直接从中取值，无需消耗额外的时间进行多次递归计算匹配。

图2 基2-FFT点数为8时递归两次后的位置映射图

数据合并部分按蝶式计算递归合并的原则，将奇偶项划分开并将单独计算的两块数据块重新合并。计算公式如式（1）所示。式中o为将要合并后的数组，u与v分别为上游处理偶数项和奇数项数据的并行实例的输出数组，w为旋转因子。

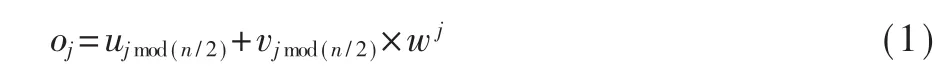
图3为Flink中蝶式计算递归次数为2时FFT并行流程方法示意图，Map算子主要负责将流元素进行位置编号，记录一帧数据的最大点数和当前位置，将其位置标签贴在每一个流动的数据项中。Partition算子负责将流元素实时拆分到不同的FFT计算算子中。在FFT计算算子中，符合要求的流数据全部到达后会触发新设计的缓存窗口，对到达的数据直接进行FFT计算。Union算子负责将计算算子的输出数据进行汇总合并。

图3 蝶式计算递归深度为2时FFT并行流程示意图

本文结合流式数据持续流动的特性，将流水线的并行思想应用于FFT并行流程方法中，实现处理时间重叠，从而降低每帧数据处理的时间。计算算子和同一深度的合并算子可以同时处理一帧的数据，而每一层深度之间可以流水线处理连续帧的数据。

由于集群性能不同和环境不同，为了让分布式流处理中的FFT并行流程具备在各个不同集群环境主动适应、自动调优的能力，需要通过试运行，确定FFT算法蝶式计算的最优递归次数，从而将每帧的处理时间降至最低。

图4是蝶式计算递归次数为1和2时FFT计算并行流程方法样例。当深度为1时，FFT计算并行实例数量为2，将整个帧中的奇数项和偶数项分别交给第一个和第二个计算并行实例独立计算。当深度为0时，整帧数据都交给一个并行实例计算，其本质上为Flink上的串行计算。深度最大为log（n），n为FFT点数。

图4 深度为1和2时FFT并行流程示意图

2.2 适用于FFT计算的缓存窗口设计

Flink现有窗口机制包括应用于事件时间的时间窗口、应用于流元素本身的计数窗口和应用于时间段数据活跃度的会话窗口，对于FFT此类高通量仪器的数据流来说，会在很短甚至相同的时间内产生大量的数据，这些双精度浮点数的数据具有极其相近甚至相同的时间戳，因此无法借助事件时间戳信息的时间窗口。而又因为 FFT计算不允许数据乱序，因此无法保障数据有序到达计数窗口。

因此，需要针对FFT这类科学计算问题，在Flink上设计特殊的缓存窗口，使其能够依据当前数据项在帧中的位置信息，在计算并行实例所要求的小块数据全部到达后触发窗口逻辑，将数据交给并行实例来进行计算。而对于负责合并的并行实例来说，由于其数据流来源为上游的两个并行实例，输出数据块必须严格遵守位置顺序以防乱序，也需要此类缓存窗口。

由于数据流可能流速过快，在负责合并的并行实例缓存窗口中，本文设有对多帧数据的缓冲队列，能够在一定程度上解决流速过快而产生如多帧数据覆盖后计算错误等问题，同时也能够在各并行实例计算速度不均衡的情况下提前将计算速度快的并行实例所产生的数据进行保存，从而节约部分通信时间。

本文缓存窗口实现方式如下，表1是其中设计的部分字段。

表1 适用于FFT的缓存窗口中部分字段设计

unionId表明了在当前这一深度中此缓存窗口所在并行实例的索引，此字段是对应所负责上一级两个并行实例的索引，例如0号并行实例主要负责合并上一级0号和1号并行实例的数据块。size字段表示负责合并的数据数量，在基2-FFT计算中，始终是两两合并，因此默认为2。isInit是判断初始化的标签。miniData是上一级并行实例所输出的小数据块。cacheQueue是多缓冲队列，队列内的每项数据以映射表的形式保存，映射表的键为所负责合并的上一级并行实例索引，映射表的值为上一级对应索引并行实例的输出数据块miniData。hasNum实时统计多缓冲队列中头部的映射表中已就绪的数据块数量。

图5是负责合并的并行实例中缓存窗口触发样例图，该并行实例主要负责上游索引为0和1的并行实例的输出数据块。阶段1时，窗口内多缓冲队列为空。在阶段2时，该并行实例接收上游输出数据＜1，data＞。＜1，data＞中的 1，表明数据流中此数据项来自上游索引为1的并行实例，data是处理后的数据块。将此data存储于队列的第一个映射表的键1所对应的值上。键0的值暂且空缺，表明未有完整匹配的数据到达。阶段3时，接收到了一项数据项＜1，data＞，依然来源于上游索引为 1的并行实例，继续缓存此数据块。阶段4时，接收来自上游索引为 0的并行实例所处理后的数据项＜0，data＞。此时队列头部映射表中的两项数据项已全部出现，弹出队列头，并将弹出后的两块数据块在此并行实例中进行合并。

图5 合并算子中缓存窗口触发样例图

3 实验结果与分析

3.1 实验配置与测试样例

由于本文主要测试的是Flink中FFT算法的各并行度时间性能和容错性能，应尽量避免带宽等因素给本实验带来的影响，因此本文主要使用Flink的Standalone模式，一个节点中设置了28个slot给不同的并行实例运行任务。具体实验节点配置情况如表2所示。

表2 实验节点配置情况

本文使用随机生成双精度浮点数作为FFT的输入数据，每组数据点数不同，均为1 000帧。本文实验所用的Flink作业拓扑图由一个Source数据源输入算子、一个 Map算子、一个 Partition算子、多个计算算子、多个合并算子和一个Sink输出算子组成。Source算子和Sink算子分别是Kafka的消费端和生产端。

3.2 实验结果与分析

该实验主要是测试FFT并行流程中处理每帧数据所需要的时间。在FFT并行流程中，多帧数据以流水线的形式在作业拓扑图中进行计算，因此每帧数据处理时间的统计均是流水线时间。

实验结果如表3所示，表中是对于不同点数的FFT数据在不同FFT计算并行度的情况下处理每帧数据的流水线时间。

表3 不同点数、不同并行度下处理每帧数据的流水线时间

表3中，按行观察，即从同一个FFT数据点数来看，随着并行度的逐渐增大，处理每帧数据的流水线时间先是逐渐减少，后来又逐渐增大。计算时间减少是由于随着计算并行度的增加，并行的算法带来了时间上的优化。但是随着并行度越来越大，FFT并行流程所自动形成的作业拓扑图越加庞大，拉长了整个计算流程，作业拓扑图中的各项并行实例、对应的窗口和流管道等组件越来越多，其本身的开销占比越来越高，因此导致处理每帧数据的流水线时间有所提高。

按列观察，即从不同的FFT数据点数来看，随着点数的逐渐增大，处理每帧数据的流水线时间基本都会成倍增加，一方面因为FFT算法的复杂度是O（nlogn），在 FFT点数总量 n翻倍的情况下，计算时间也因此会同步增加；另一方面是由于数据量的提高，在整个并行流程中传输一帧数据所需要的时间大大增加，特别是各并行实例窗口的触发延时和并行实例之间的传输也需要更多时间，增加了时间的损耗。

从整体来看，随着点数的逐渐增大，时间消耗最小的最优并行度先增大后减小。在点数为16 384时，并行度为2的情况下处理每帧数据的流水线时间最小，成为所有并行度下的最优并行度；在点数分别为 65 536、131 072、262 144时，最优的并行度向后推移为8；在点数更大时，最优的并行度反而减小。并行度逐渐增大的原因为在点数较小的情况下，每帧的数据量较小，使用并行算法的必要性不高，因为并行算法会带来一定的开销，对时间的优化不明显。但在点数增加、每帧的数据量提高时，使用并行计算带来的时间优化越来越明显，因此计算所需要的时间也越来越少。在点数增加到一定规模如1 048 576后，最优并行度反而下降。本文探究最优并行度变化的原因如下。

本文统计了并行度为1时不同点数下每帧数据完整的计算时间和通信时间，如表4所示，以及点数为131 072时不同并行度下每帧数据的计算时间和通信时间，如表5所示。此处总时间为整帧数据全部的时间，计算时间包括FFT计算时间、多级合并时间，通信时间包含序列化反序列化时间、流通道数据传输时间、并行实例输入缓冲区和输出缓冲区等待时间等。

如表4所示，在并行度不变、点数逐渐增加到巨大规模时，计算每帧数据所需的通信时间增加幅度远大于FFT点数规模增加所导致的计算时间增加的幅度。因此表3中最佳并行度会随着点数增加到一定程度时降低，是因为此时通信时间逐渐占据了主要部分。如表5所示，在点数不变的情况下，并行度逐渐增加会使一帧的总时间增加。其中并行度增加时，由于每个并行实例处理的数据减少，因此小份数据的计算时间会急剧降低，但是并行度增加时会拉长整个作业拓扑图，FFT计算的深度会增加，带来更多的通信阶段，通信时间也会因此增加。因此需要试运行来自动决定不同FFT点数的最佳并行度，从而将每帧数据的流水线计算时间降至最低。

表4 并行度为1（Flink中串行）时不同点数每帧数据计算时间和通信时间

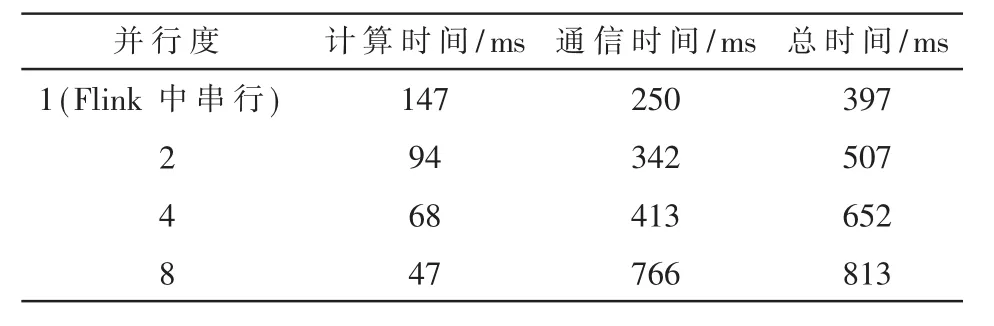
表5 点数为131 072时不同并行度每帧数据计算时间和通信时间

图6所示是FFT不同点数下，Flink中串行的计算时间和对应最优并行度的计算时间对比图。从实验结果中可以看出，本文设计出的FFT并行流程在不同点数的最优并行度下与Flink上串行的FFT算法相比，处理每帧数据的流水线时间大大降低。

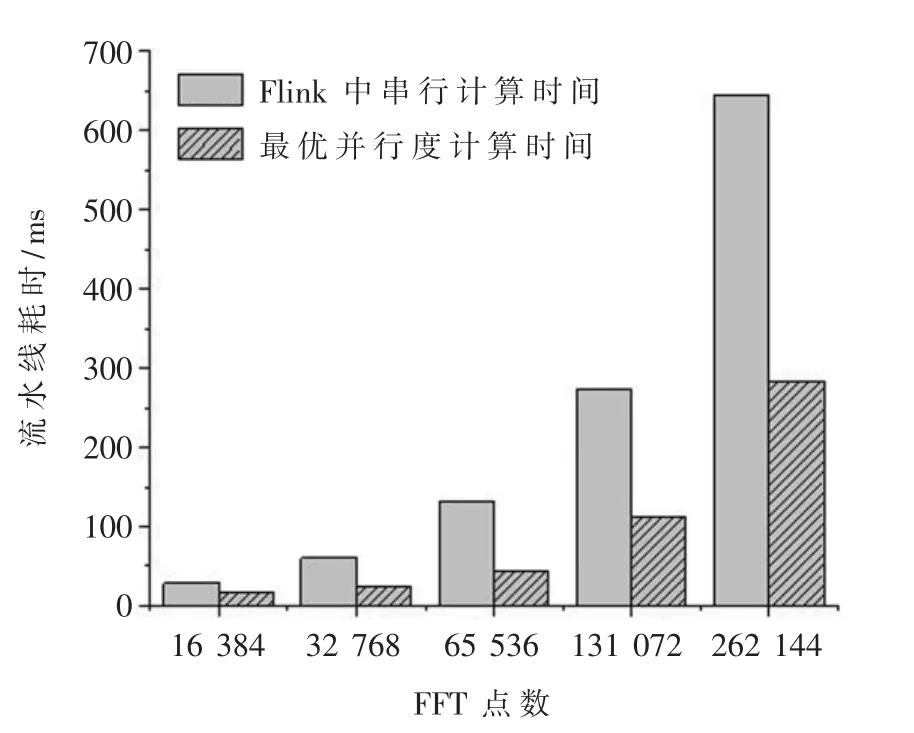
图6 Flink中串行计算时间和最优并行度计算时间对比图

4 结论

本文将FFT的计算特点与分布式流处理相结合，提出了一种基于Flink的FFT并行流程方法，同时在Flink中设计了适用于FFT的缓存窗口，使得通信时间和计算时间有部分时间重叠，加快FFT处理时间。实验结果表明，本文在Flink上FFT并行流程中降低了每帧的处理时间，提高了计算效率。下一步的工作重点是对FFT并行流程中的流水线进行进一步的优化。