基于教育测评数据的个性化认知诊断研究

刘霞林，陈莉君，舒新峰，梁 琛

（西安邮电大学 计算机学院，陕西 西安 710121）

0 引言

教学过程中需要分阶段诊断学生学习中存在的问题和不足。传统的学业诊断方法多采用分数诊断法，即通过考试或测验考察所学内容的掌握程度，然后对个体数据如分数、排名和整体数据如班级平均分、标准差等进行计算及分析。这种方法侧重学生考题得分，忽略了试题题型、难度、内容以及评分标准的差异，只能提供单一笼统的诊断信息用于诊断评估［1］，难以深入挖掘测评数据，获取代表学生认知水平和知识掌握程度的足够信息。当考试人数、题目数量、题型数量较多时，计算的工作量增长很大，难以保证所有数据百分之百可靠，从而影响诊断准确性和时效性［2］。个性化学习应该针对学生的个性特点和发展潜能，让学生获得自由的学习空间，达到知识和认知能力的协调发展［3］。这就要求对学生的学习状况展开多角度、多层面的个性化诊断，为指导和促进学习提供全面而有价值的信息和资料。随着教育评价、认知科学、人工智能的发展，完善测评数据系统，创新教学诊断方法和手段，深度分析测评数据、挖掘测评数据的可利用价值，为学习者和教育者提供基于学习者个性差异的诊断报告成为可能。个性化教学诊断不仅可以满足学习者个性化学习需求，而且可以帮助教师制定准确的教学目标、选择适宜的教学内容，在教学过程中不断改善教学设计、调整教学进度。

认知诊断（Cognitive Diagnosis，CD）用于测量个体的知识 结 构（Knowledge Structure）和 加 工 技 能（Processing Skills），其目的是探讨个体的心理加工机制，诊断个体当前的认知状态，为个体因材施教、开展有针对性的补救提供服务［1-4］。如何对学习者的学习活动进行有效的认知诊断，从而检测其知识、技能和思维能力的真实现状，是当前要解决的主要问题。本文基于教育测评数据建立个性化认知诊断模型，从教学目标和知识点两个维度分析测评数据，为学生和教师提供个性化的认知诊断报告，为教学提供科学及时的反馈。

1 相关研究

1.1 教育测量理论

教育测量是认知诊断的基础。教育测量在教育评价、教育诊断等方面发挥着重要作用［5］。由于测量对象的特殊性，教育测量具有以下特点：无法直接测量，测量单位不固定，要为实现教育目的服务，测量对象复杂。教育测量理论一般分为经典测量理论、概化理论和项目反应理论3 大类，经典测量理论又称真分数理论，它测量被测者的特征（知识、能力、个性）的真实值，但测量结果受抽样样本的变动影响较大，且对测试误差无法深入研究；项目反应理论是通过项目反应曲线再综合其它资料，分析试题和被测者之间的关系，适合高中低不同能力的学习者参加测验。该理论需要建立复杂的数学公式，实现难度较大，而且样本容量对精确性影响很大。概化理论认为应该从测量的情境关系中考察测量工作，该理论可以更好地控制测量误差，但是与经典测量理论一样仍属于随机抽样理论，容易受到随机误差影响。

1.2 教育测评数据选取及收集

在测评中收集的数据称为教育测评数据，主要指学习过程中围绕学习个体收集的数据［6-7］。选取哪些数据作为测评数据与学习评价的标准和教育测量的技术水平有关。文献［7］认为不能通过统一的评价标准来衡量学习成效，不同学习者的评价标准、维度和指标应不同，应提供多种评价方案供学习者自主选择或系统自动匹配。基于此，在一个在线学习平台上，初级学习者评价方案所选用的测评数据有学习时间、在线批注、编辑内容、发表评论等。由于教育测量的特殊性和复杂性，对教学过程中全部数据进行采集存在障碍，除了期中考试、期末考试所能收集的总结性测评数据外，常态化练习和阶段性测验收集到的形成性测评数据都能大大丰富测评数据，为个性化诊断提供必要的数据基础；文献［8］认为测评数据包括试题与学习者两个维度，其中试题维度数据以知识点为核心，包括知识点内容、类型、难度、区分度、知识点之间的关系等，学习者维度数据以学生作答情况为主，包括答题正误情况、解题过程、成绩、排名等；文献［9］为个性化网络学习设计了一套具有层次结构的学习评价指标体系，涵盖学生的个性特征、资源利用、交互与协作、阶段性学习效果、知识应用等5个方面，为此选取的测评数据有：自我学习能力认识、学习目标认识、学习平台在线时长、与该课程有关的其它在线时长、提问次数、回答问题次数、上传学习资料次数、答疑次数、问题难度、期末考试成绩、课程设计成绩、毕业设计成绩等。随着线上学习平台的普及和发展，越来越多的学习行为数据可通过学习平台记录和收集，测评数据范围在不断扩大，数据粒度变得越来越小，数据收集的技术手段越来越先进，为建立测评数据系统提供了支持条件。

1.3 个性化认知诊断模型与个性化认知诊断系统

研究者已从各种不同的角度提出近百种认知诊断模型，如规则空间模型、统合模型、确定性输入、噪音“与”门模型、属性层次方法等。这些模型的共同特点是计算复杂，需要大量的运算才能实现认知诊断，而且不易理解，一定程度上阻碍了其广泛应用。文献［8］实现了一个基于形成性测评数据的个性化学习评价系统，对学习平台上生成的形成性测评信息进行归类整理并纳入评价标准。根据学习目标和知识掌握程度要求的不同，构成个性化评价方案，从学习态度、学习活动、内容交互、资源工具、评分反馈等多方面对学习者的学习成效进行评价；牟智佳［10］构建了基于电子书包的个性化评价系统，设计基于教育大数据的个性化评价层次塔，从课程内容学习、参与互动交流、考试与作品、课外资源学习4 个方面进行评价，并通过云管理层实现对教育云服务平台、云存储池和云集群计算平台的调度和管理；Karamehic［11］、Yankovskaya 等［12］设计一个以证据为中心的评价系统，该系统以形成性评价或总结性评价为目的，提供与评价目的相适应的评价证据；文献［13］提出一个学习和测试智能系统（Learning and testing intelligent system，LTIS），该系统利用基于认知组件（Cognitive compo⁃nent）的混合诊断测试（mixed diagnostic tests，MDT）方法对学习者的专业知识和技能进行评估。

虽然国内外学者建立了较多的个性化认知诊断模型和系统，但在简洁性和诊断属性设计上还存在不足，也缺乏针对教学目标达成情况和知识点掌握情况的个性化认知诊断。本文设计面向教学目标和知识点的认知诊断属性，基于云学习平台上积累的教育测评数据建立个性化认知诊断模型，以实现教学过程中学习者的知识和认知水平的快速诊断。

2 理论基础

建立个性化认知诊断模型，首先需要确定认知诊断属性，为了诊断教学目标是否达成，本研究采用布鲁姆教学目标分类学支撑学习者的认知维度；为了诊断知识的掌握情况，采用知识点作为学习者的知识维度。以Q 矩阵作为认知诊断方法，形式化描述学习是否达到教学目标要求及知识点是否完全掌握。

2.1 布鲁姆教学目标分类学

在布鲁姆教学目标分类学基本版基础上，毛秀珍［14］对认知维度进行扩充，形成布鲁姆教学目标分类学修订版。在修订版中，两个认知维度分别是知识和认知过程，知识维度包含事实性知识、概念性知识、程序性知识和元认知知识4 个类别；认知过程维度包括记忆、理解、应用、分析、评价、创造6 个类别。本研究利用布鲁姆教学目标分类学修订版实现教学目标的表述、测量以及达成诊断：①根据教学目标设计试题，按照知识和认知过程两个维度对每一道试题进行分类；②设置目标属性，将知识和认知过程维度作为两个测量属性，计算学生对于知识维度各层级和认知过程维度各层级的掌握概率；③基于布鲁姆教学目标分类学描述教学目标含义，对②中计算得到的掌握概率进行阐述，对教学目标是否达成进行诊断，从而完成个性化认知诊断。

2.2 Q 矩阵理论

Q 矩阵是一种基于规则空间模型的认知诊断模型，它包含多种类型矩阵，其中Q 矩阵是描述测验项目与属性间关系的矩阵，A 矩阵是反映属性间直接关系的矩阵，R 矩阵是反映属性间直接关系、间接关系和自身关系的矩阵。IRP 是被测试者对测验项目的作答反应。Q 矩阵理论在量化不可观测数据方面有独特优势，可以把不便测量的认知属性与可直接测量的学生试题作答情况联系起来，为了解学生的认知水平提供条件。

在布鲁姆教学目标分类学基础上，利用Q 矩阵理论，为学生知识的掌握情况和认知水平的诊断提供计算方法。通过系统分析学生的测评数据对目标属性进行诊断，实现面向教学目标和知识点的个性化认知诊断。

3 基于教育测评数据的个性化认知诊断建模

本研究以教育测评数据为数据来源，按照布鲁姆教学目标分类学描述教学目标，根据Q 矩阵理论建立所测项目与属性间关系的矩阵和项目反映矩阵，通过计算面向教学目标和知识点的属性掌握概率建立个性化认知诊断模型。

3.1 测评试题分类与知识点分类

试题是教师为考核教学目标是否达成而编写的用于学生作答的测验项目，是教学目标的集中体现。为使认知诊断结果能准确反映学生对相关教学目标的达成情况，使用期中考试、期末考试及阶段性测验中的试题作为描述教学目标的依据，将在考试/测验中收集到的数据作为测评数据，以此为基础构建个性化认知诊断模型。具体内容为：①试题按教学目标分类，从而将反映教学目标的试题内容转换为目标属性。按照布鲁姆教学目标分类学，将试题内容所描述的教学目标中的动词和名词分别对应到两个认知维度（知识和认知过程）的各层级，实现教学目标到目标属性的转换。例如，“运用进程调度策略解决调度问题”这一教学目标中，动词“运用“与分类学中认知过程维度的“应用”这一层级相对应，名词“进程调度策略”与知识维度的程序性知识这一层级相对应，该教学目标属于应用程序性知识类别，它的两个目标属性分别是“程序性知识”和“应用”；②试题按知识点分类，实现试题内容到知识点属性的转换。为诊断学生对知识点的掌握情况，反映试题和知识点的对应关系，将教材上内容所涉及的知识点表示出来构成知识点集合，并把每一道试题拆分成一个或若干个知识点并与知识点集合进行耦合，构成试题—知识点矩阵。

3.2 基于Q 矩阵的认知诊断计算

属性掌握概率模型是一种容易理解、计算较为简单的认知诊断模型。根据该模型，学生必须掌握一个试题所涉及的所有目标属性才能答对该试题，可以先观察学生在涉及某个属性的所有试题上的作答情况，定性估计学生对该属性的掌握情况，然后用试题答对概率定量计算属性掌握概率的值，值越大说明学生对该目标属性的掌握越好。本文基于Q 矩阵的属性掌握概率模型，实现对教学目标属性值和知识点属性值的计算，从而进行个性化认知诊断。计算步骤如下：

（1）假设在某次考试/测验中试题总数为M，试题集合为：

学生总数为N，学生集合为：S={s1,s2,…,sN}，则利用S×T 构成项目反应矩阵R：

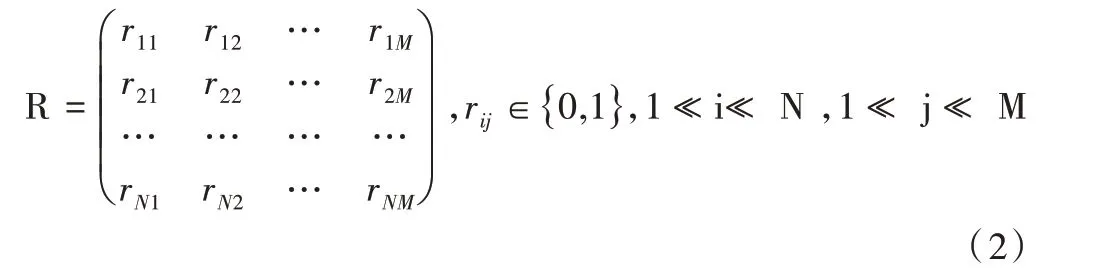
其中rij=1 表示学生si答对了试题tj，否则rij=0。

（2）假设试题涉及的教学目标属性数为L1，教学目标属性集合为：O={o1,o2,…,oL1}，知识点属性数为L2，知识点属性集合：K={k1,k2,…,kL2}，则利用T×O 和K×O 可构成描述试题与所测属性关系的Q 矩阵Q1 和Q2：

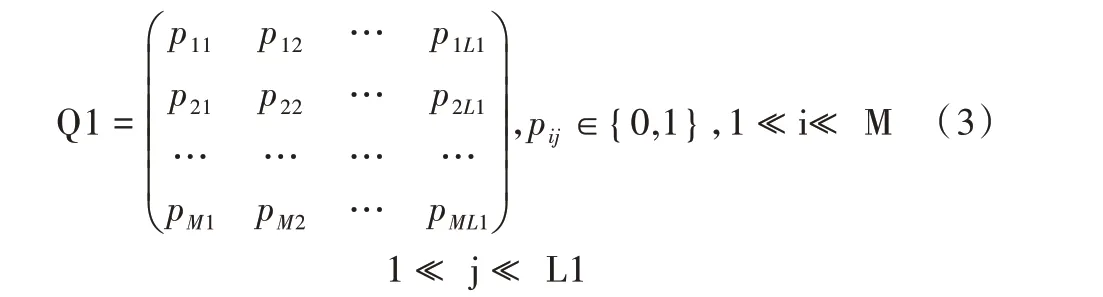
其中，pij=1 表示试题ti涉及了教学目标属性oj，否则pij=0，Q2 与Q1 类似。

（3）根据第（1）和第（2）步得到的矩阵R、Q1 和Q2，分别计算出每个学生在每个教学目标属性上答对的试题个数和每个知识点属性上答对的试题个数：

mij表示学生si在教学目标属性oj上答对的试题个数，N2 与N1 类似。

（4）学生si在教学目标属性ok上的答对频率计算为fik=若Sk=0，则fik=0。其中表示涉及属性ok的试题总数。学生si在知识点属性kt上的答对频率为git=若St=0，则git=0。其中表示涉及属性kt的试题总数。将学生si答对试题tj的概率估计为试题tj所涉及所有教学目标属性的答对频率与所有知识点属性的答对频率之乘积：

（5）将学生si对教学目标属性ok的掌握概率估计为涉及教学目标属性ok且学生si作答所有试题答对概率之和与涉及属性ok的所有试题答对概率之和的比值：

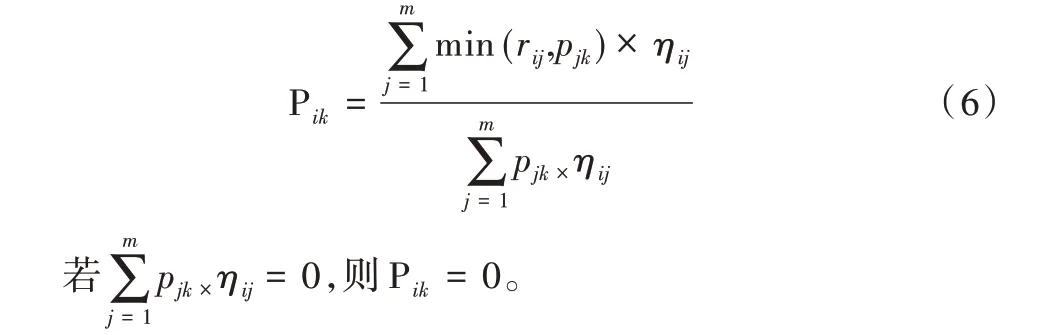
学生si对知识点属性kt的掌握概率P'it的计算与Pik类似。

3.3 个性化认知诊断模型生成

在确定研究目标、研究数据以及研究方法基础上对个性化认知诊断的核心内容进行描述，并由此构建个性化认知诊断模型，如图1 所示。该模型基于教学目标和知识点两个维度，在教学目标维度使用布鲁姆教学目标分类学的方法描述教学目标，利用学生答题数据对教学目标达成的客观反映计算学生在每个层级的教学目标达成度，从而度量学生内在的认知水平。在知识点维度，以知识点掌握情况为目标，利用学生答题数据对知识点掌握的客观反映度量学生外在的知识点掌握程度。在此基础上进行包括教学目标达成诊断、知识点掌握程度诊断、学习风险预警以及成绩、排名等反馈在内的个性化认知诊断。最终，将诊断结果反馈给师生，使教师和学生可从教和学两方面同时入手改善认知能力和知识点的薄弱之处。由于采用了真实的教育测评数据，所以诊断结果能够更加客观地反映学生的认知水平和知识点掌握程度；由于使用了简洁高效的基于Q 矩阵的属性掌握概率算法，使得模型在学生规模和试题规模有较大增长的情况下仍具有较好性能。

4 验证与分析

4.1 研究对象与数据选取

本研究以西安邮电大学广电专业两个班级65 名学生为研究对象，以在云学习平台上收集到的10 次测试活动的测评数据作为数据来源对模型进行验证和分析。测评数据包括试题和学生两个维度。试题维度的数据以教学目标和知识点为核心，试题数据共选取32 道试题，涉及操作系统原理课程的操作系统概述、进程管理共5 章教学内容，题型为选择、填空、简答、计算，通过分析教学内容和课程特点，将教学目标划分为记忆事实性知识、记忆概念性知识等18 个类型（没有创造类、记忆程序性类和记忆元认知类），同时，从全部教学内容中提取出操作系统概述、多道程序设计、分时系统等16 个知识点，最后将每道试题归属到相关的教学目标和相关知识点。学生维度以学生的作答情况为核心，包括答题正误情况、解题过程、成绩、排名等。

Fig.1 Personalized cognitive diagnosis model based on educational evaluation data图1 基于教育测评数据的个性化认知诊断模型

4.2 教学现状分析

之前主要采用传统的教学诊断方法即分数诊断法，由于非本专业必修课，因此只有期末考试作为唯一考核。考试结束后，将学生的总分进行排名，通过统计分数段人数和比例，计算平均值、标准差力求掌握班级整体情况。这种诊断方法忽略了试题题型、难度、内容以及评分标准的差异，诊断信息比较单一，难以深入挖掘测评数据，几乎没有对学生进行个性化诊断。

4.3 教学目标达成度的个性化认知诊断

利用个性化认知诊断计算步骤进行如下计算：①构成Q 矩阵和项目反应矩阵R。对试题进行分析，将试题分别与18 个教学目标进行耦合，得到试题和教学目标属性的关联矩阵Q1。对学生的答题情况进行分析，构成项目反应矩阵R；②利用矩阵乘法计算每个学生在各教学目标属性上答对的试题个数，即得到矩阵N1；③在学生对教学目标属性答对频率的基础上计算学生试题的答对概率；④计算学生对各教学目标属性的掌握概率，结果见表1。表1 中“理解事实性知识”元素均为0，表示没有涉及该教学目标的试题，“理解概念性知识”元素为1 表示学生完全达到了相应教学目标要求。

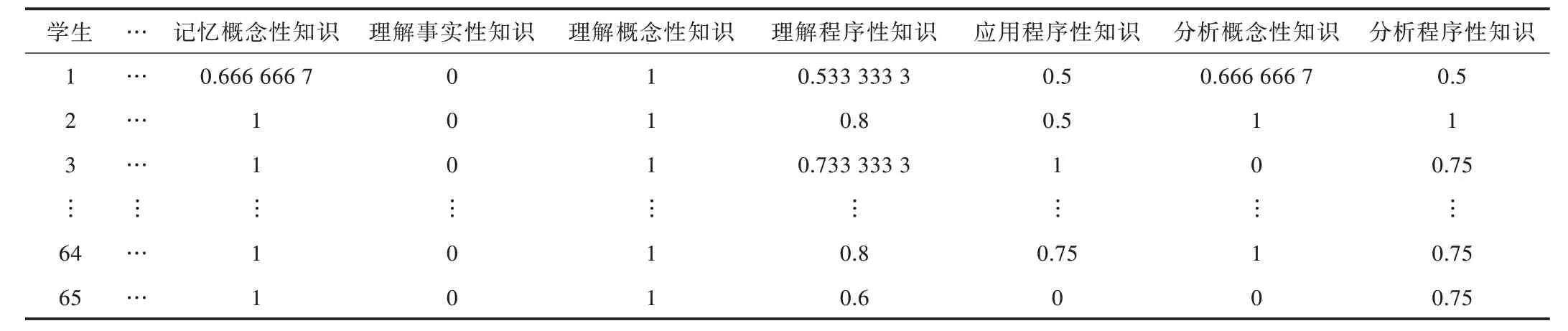
Table 1 Estimated value of probability of mastering teaching objectives表1 教学目标掌握概率估计值

从班级整体看，学生对布鲁姆教学目标的达成度在知识和认知过程两个维度均随着属性层级的升高而降低。在知识维度认知过程一定的情况下（比如“理解”），学生对“事实性知识”掌握最好，“概念性知识”次之，“程序性知识”最差。在认知过程维度，知识类型一定的情况下（比如“概念性知识”），随着对学生认知能力要求的提高，教学目标达成度逐渐降低，详情如图2 所示。从学生个体看，将某个学生的达成情况与班级整体进行对比，可以诊断出学生与班级整体水平之间的正负距离。比如，学生60 在“理解事实性知识、概念性知识、程序性知识”“应用及评价程序性知识”方面优于班级平均水平，而在“记忆、分析和评价概念性知识”以及“分析程序性知识”方面低于班级平均水平，如图3 所示。该名学生应该加强对基本概念的学习，提高程序性知识的分析能力。将学生之间的达成情况进行比较，学生之间可以更有针对性地优势互补。比如学生5在多个教学目标上与学生28 存在较大差距，可以在二者之间形成有效的生—生互动。而在“分析概念性知识”方面，后者又可以向前者分享学习经验，见图4。面向教学目标的学生个体之间的比较，打破了传统的优等生和后进生的界定标准，更易于在学生之间找到互补空间，促进学生互动。

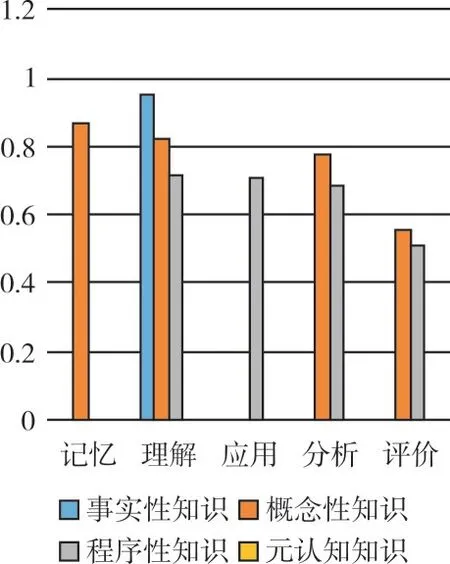
Fig.2 Attainment of the overall teaching objectives of the class图2 班级整体教学目标达成度

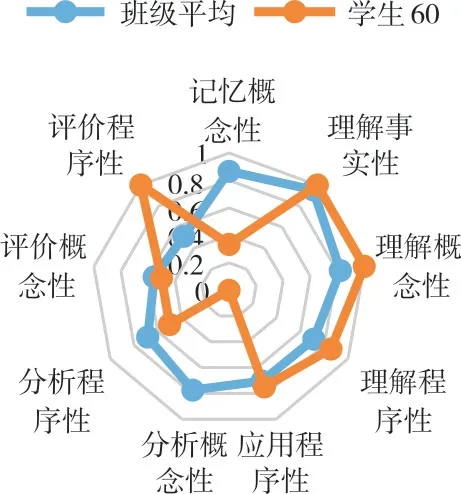
Fig.3 Comparison of the achievement of teaching objectives between individual students and class as a whole图3 学生个体与班级整体教学目标达成度比较

Fig.4 Comparison of achievement degree of teaching objectives among individual students图4 学生个体之间教学目标达成度比较

4.4 知识点掌握程度的个性化认知诊断

利用个性化认知诊断计算步骤进行计算：①构成Q 矩阵和项目反应矩阵R。对试题进行分析，将试题分别与16个知识点进行耦合，得到试题和知识点属性的关联矩阵Q2；②利用矩阵乘法，计算出每个学生在各知识点属性上答对的试题个数，得到矩阵N2；③在学生对知识点属性答对频率基础上计算学生对试题的答对概率；④计算学生对各知识点属性的掌握概率，结果见表2。

Table 2 Knowledge points grasp probability estimation value表2 知识点掌握概率估计值

从整体看，学生对知识点掌握程度由高到低依次为：操作系统概述→重定位→用户接口→虚拟内存→死锁→实时系统→请求分页→批处理系统→进程状态→进程同步→进程结构→分页管理→分时系统→多道程序设计→段页式管理，班级整体对知识点的掌握情况见图5。从图中可以看出，大部分知识点掌握程度都在0.7 以上，说明大部分学生基本掌握了所学内容。“段页式管理”掌握程度最差，只有0.338 462。该知识点综合了分段管理和分页管理两个知识点内容，分段管理和分页管理具有较为复杂且容易混淆的管理机制，造成大部分学生在学习该知识点时遇到困难，教师应给予该知识点更多的指导，学生也应加强该知识点的练习。对学生在每个知识点掌握情况进行对比，如学生6 在“进程状态”知识点上掌握概率的估计值只有0.333 333 3，在“进程同步”知识点上的估计值只有0.25，大大低于其它知识点估计值，而且该学生在多个知识点上低于班级平均水平，需要提出预警。学生60 在“批处理系统”等多个知识点上估计值为0，排除缺考原因，需要提出强预警。将学生之间的知识点掌握情况进行比较，有助于学生之间更有针对性地优势互补，如图6、图7 所示。

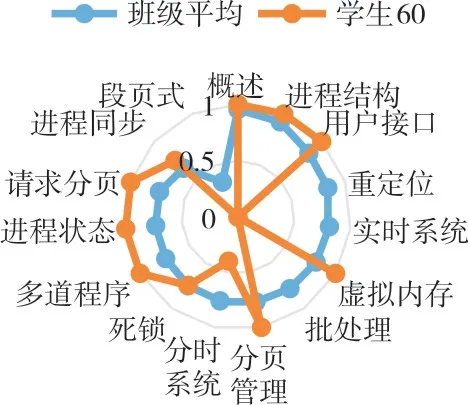
Fig.5 Comparison of mastery of knowledge points between individu⁃al students and class as a whole图5 学生个体与班级整体知识点掌握程度比较

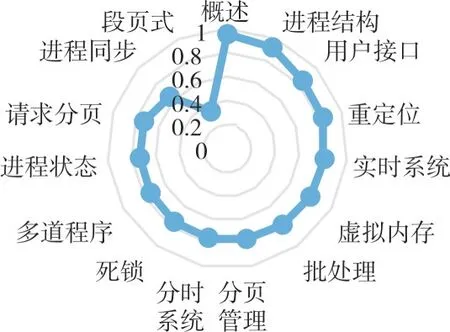
Fig.6 Master degree of overall knowledge points in class图6 班级整体知识点掌握程度

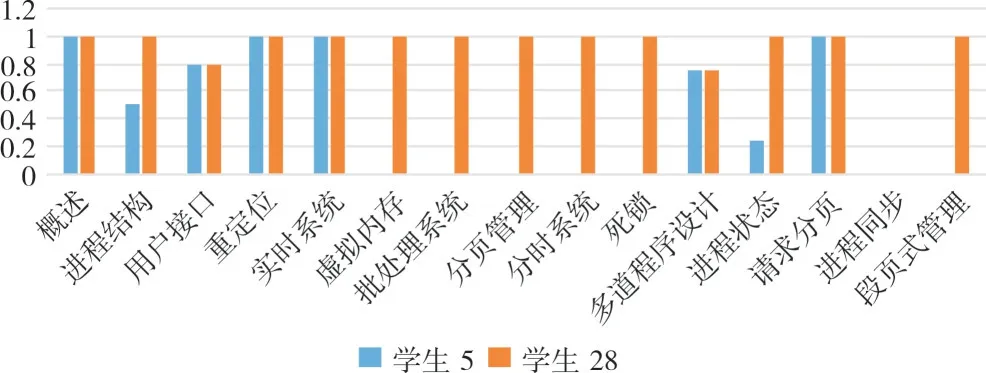
Fig.7 Comparison of mastery of knowledge points among students图7 学生个体之间知识点掌握程度比较

4.5 个性化认知诊断应用

由于本研究采用的测评数据来源于在线学习平台，要求教师和学生具备使用网上学习平台技能，因此适合在高校开展个性化认知诊断。从诊断方法上看，虽然基于Q 矩阵的属性掌握概率模型相比其它认知诊断模型容易理解、计算简单，但仍包含了多个较为复杂的计算步骤，教师需要掌握Q 矩阵理论和属性概率理论才能应用该模型。

5 结语

基于教育测评数据的个性化认知诊断可为学习者的个性化学习和教师的因材施教提供保障。布鲁姆教学目标分类学为诊断学习者的认知水平提供了较好支撑，基于Q 矩阵的属性概率计算可以简洁高效地支持个性化认知诊断模型的计算需要。本文从面向教学目标和知识点目标属性设计、个性化认知诊断计算流程、个性化认知诊断模型生成3 个方面，对基于教育测评数据的个性化认知诊断建模进行了阐述，并以布鲁姆教学目标分类学和Q 矩阵理论为基础建立个性化认知诊断模型。以西安邮电大学广电专业两个班级65 名学生为研究对象，将在云学习平台上收集到的10 次测评数据作为数据来源对模型进行了验证。后续将把本研究取得的成果整合到教学平台中，对学习者进行及时的个性化认知诊断及反馈，帮助教师制订教学目标、调整教学进度、完善教学设计，最终提高教学效果。