基于ABiLSTM 与XGBoost 组合模型的交通时间预测

宋瑞蓉，路树华，王斌君，仝 鑫

（1.中国人民公安大学 信息网络安全学院，北京 100038；2.山东省日照市人民医院，山东 日照 276800）

0 引言

交通时间预测旨在利用已有的交通时间数据对未来出行时间进行预判。交通时间预测不仅在日常出行中具有重要意义，而且便于交通部门在交通拥堵发生之前，及时预测并采取有效的避免措施。此外，公安机关在侦破案件时利用交通时间预测能够锁定嫌疑车辆经过某地点的时间范围，从而缩小排查范围，提高工作效率，减少工作量。围绕交通时间预测开展的研究基本可以分为两类：时序方法和非时序方法。

时序方法重点考虑了交通问题本身具有时序数据的特点，可以借鉴时序数据处理方法及模型，因此，时序方法在交通时间预测领域备受青睐。ARIMA（Autoregressive In⁃tegrated Moving Averrage Model）是一种经典的时序预测方法，文献［1］将ARIMA 应用到交通时间预测任务中，使得ARIMA 利用所学习到的交通时间随时间变化关系预测未来时间段的交通时间，而不需要其它任何辅助属性。LSTM处理序列化数据具有很好的效果，文献［2］将LSTM 应用于交通时间预测任务中，并充分考虑了相邻时间步的结果对此刻预测结果的影响；文献［3-4］将注意力机制与卷积神经网络相结合用于交通时间及交通流量预测；文献［5］将注意力机制与LSTM 模型相结合，对每一时间步赋予不同权重；文献［6］将结合了注意力机制的LSTM 模型进行改进，并用于解决交通时间预测任务，相较于LSTM 只考虑一个方向的传递，双向长短期记忆网络（BiLSTM）是前向LSTM 与后向LSTM 的结合，能够充分考虑相邻时间步对预测结果的影响；文献［7-9］将注意力机制与BiLSTM 相结合，应用于不同领域。

交通时间预测领域常见的非时序方法有线性回归、随机森林、支持向量回归（SVR）以及K 近邻算法（KNN）等［10］。这类方法的优点在于只需给出相关属性即可进行预测，而不需要给出相邻时间段的信息，在一些较为简单的数据集上有较好的表现；缺点是在交通时间预测中会遗漏掉一些时序信息，并且对于一些属性间关系较为复杂的数据集不具有很好的预测效果。在机器学习方法中，极端梯度提升（XGBoost）模型常被用于分类和回归任务，通过多棵决策树预测最终结果，并且每增加一棵树都能确保目标函数值有所下降，在多种任务中往往具有较好表现。文献［11］将XGBoost 模型应用于短时交通流预测，采用hyperopt 方法进行自动调参，在所构造的时间序列与时空序列上分别进行实验，均表现出了较好的效果；文献［12］将遗传算法与XG⁃Boost 模型相结合，利用遗传算法良好的全局搜索能力为XGBoost 进行调参，提高模型表现效果。

此外，许多研究基于组合模型开展。常见的组合模型使用时间序列方法与机器学习方法相结合。文献［13］将LSTM 模型与XGBoost 模型相结合，利用误差倒排法对不同模型赋予不同权重，由两个模型共同决定最终预测结果；文献［14］首先利用LSTM 处理时序化特征，然后将其预测结果作为一项新的特征与其它基础特征共同用于XGBoost模型预测，结果相较于单一模型有所提升；文献［15］利用卷积神经网络提取特征，然后使用果蝇算法优化XGBoost模型参数，将经过特征提取的数据投入参数被优化的XG⁃Boost 模型中进行预测，在保证预测准确度的情况下，提升了预测效率；文献［16］将时序方法Holt-Winters 与线性回归相结合用于高铁短期客流预测。利用时间序列模型可以关注数据随时间变化的特征，机器学习方法能够很好地挖掘属性时间的依赖关系，这两种模型结构相差较大，因此在一定情况下可以综合两种模型优势，提升预测效果。

本文将BiLSTM 模型与XGBoost 模型相结合，其中BiL⁃STM 模型中添加了注意力机制，使得模型能够对不同时间步赋予不同权重的关注，XGBoost 模型使用了两种调参方式，分别为hyperopt 方法自动调参和利用遗传算法进行调参，将两种调参方法的结果进行对比，选用准确度更高的模型与改进的BiLSTM 模型进行组合，从而相较于单一模型提升了预测效果。

1 改进的BiLSTM 模型

1.1 BiLSTM 模型

循环神经网络（RNN）经常被用于具有序列化特征的数据处理，每一个隐藏层神经元h是由当前输入与上一时刻的隐藏层神经元的输出所组成，这使得数据能够向后传递。但同时也带来一大问题，这种长期依赖会导致网络记住大量冗余信息，权重更新缓慢，一些重要信息会随着节点的增多而被遗忘。长短期记忆网络（LSTM）是RNN 的一种改进，可以解决RNN 存在的上述问题。LSTM 由输入门、输出门、遗忘门和内部记忆单元组成，如式（1）-式（6）所示。在设定时间步长后，可以对这些时间步内的特征进行自适应地关注，从而解决时间序列的交通预测问题。

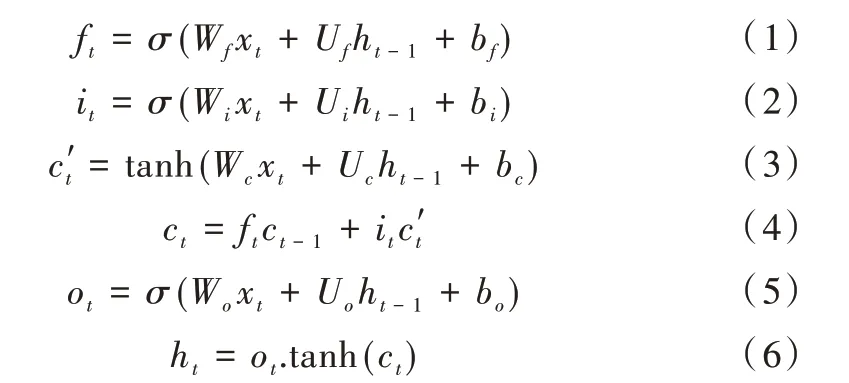
式（1）表示遗忘门，可控制丢弃一些不重要的信息，减少网络传递中大量的冗余信息；式（2）表示输入门，可用来控制输入xt和当前状态ht-1更新到记忆单元的程度大小；式（3）和式（4）是内部记忆单元，将上述遗忘门和输入门的信息加以组合，决定哪些信息可以被更新；式（5）和式（6）是输出门，是为了计算当前的隐藏层状态，以便网络继续向后传递。相较于RNN 共享同一组权重与偏置会导致梯度爆炸和消失问题，LSTM 对每一个门都各自共享了一组权重与偏置，这样能够控制一些信息的流入和流出，从而使得整个网络更好地把握序列信息之间的关系。

双向长短期记忆网络（Bidirectional Long Short-Term Memory，BiLSTM）是前向LSTM 与后向LSTM 的结合，它主要处理有时间序列关系的流数据，在保留数据顺序性特征的同时充分地挖掘和利用上下文信息。BiLSTM 中每一个单元的结果受前后两个单元的影响，在前向LSTM 中，此刻单元状态At受上一单元At-1结果的影响，在后向LSTM 中受At+1状态的影响，两个状态共同作用得到此时的结果［7］。前向LSTM 与后向LSTM 的结合更加充分地利用了时间序列的上下文信息，使得预测结果更加准确。

在交通时间预测任务中，一个时间点的交通时间和与之相邻的前、后时间点都有关系，那么采用双向预测模型便具有很强的可解释性。例如，一条路在9：00 时刻发生拥堵，那么9：15 的通行时间也一定会受到影响。LSTM 利用单向传递的特征，通过前5 个时间步的交通时间预测当前时刻。但这种传递方向并不只是单向的，如果得到9：30 的通行时间，发现此时道路是阻塞的，则有理由相信9：15 时刻的道路状况也是如此，从而预测出相应的交通时间。当这种传递具有双向性时，同时考虑与预测时刻相邻的前、后时刻对该时刻的影响，将会使结果更加具有信服力。

1.2 注意力机制

注意力模型通过神经网络模型与注意力机制的结合，提高模型对特征的关注能力。注意力机制借鉴于人类的视觉注意力机制，人类会在整个视觉范围内将注意力集中于最重要的部分，从而有效地快速筛选出对自身最有意义的信息，极大地提高了信息处理准确率。神经网络中添加的注意力机制也是为了达到这样的效果，快速关注重要信息，减少无关信息对结果的影响。

具体而言，在交通时间预测任务中，添加注意力机制是为了对每一个时间步赋予不同权重的关注，对于一些较远的时间步减少关注，对于相邻时间步赋予更多关注，从而使预测结果更加准确。式（7）—式（9）是描述注意力机制的神经网络，其中，H是BiLSTM 网络的输出，W与w是注意力机制神经网络中的权重，一开始被随机初始化，通过模型训练不断更新得到，α是注意力权重向量，r表示BiL⁃STM 网络的输出与注意力机制进行加权求和，代表网络最后输出，具体网络结构如图1 所示。

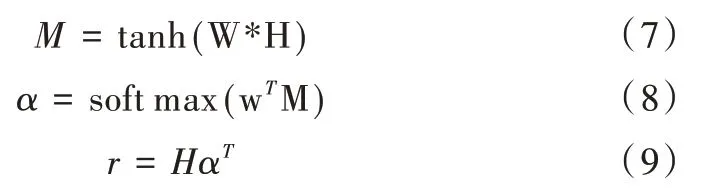
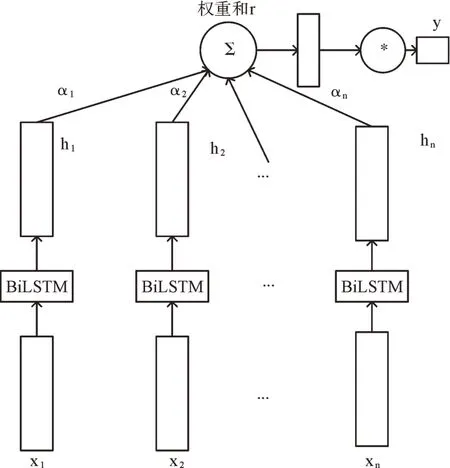
Fig.1 BiLSTM network structure with attention mechanism added图1 添加了注意力机制的BiLSTM 网络结构

1.3 ABiLSTM 模型

某一时刻的交通时间受相邻时间段影响，BiLSTM 网络可以充分利用该时刻前后的信息预测当前时刻的交通时间，但周围时刻对于此时刻的影响程度并不相同，若模型对每一时间步都进行同等程度的关注，则将失去了焦点和重点。为解决该问题，本文建立了结合注意力机制的BiL⁃STM 网络（Attenton-based BiLSTM，ABiLSTM），在BiLSTM网络的输出层上添加了注意力层，依据每一时间步对待预测时间点的贡献程度不同，为每一时间步训练出一组权重向量，将双向LSTM 网络的输出与注意力权重进行加权求和作为模型最后的输出结果。BiLSTM 中时间步长设置为5，每一个时间步中包含4 个属性，模型经过训练，会对这些特征分别计算出相应权重。

本文所选取的实验数据集来自英国公路局提供和管理的路段通行时间数据，每15min 为一个时段，记录一条数据。经过筛选共保留5 个属性，分别为日期类型、时间类型、平均速度、交通流量以及通行时间。选取AL1053、AL1249、AL1253 等20 条公路在2014 年1 月份的交通数据，其中每条公路有2 973 条数据，其中80%划分为训练集，20%为测试集。在每条公路上分别使用BiLSTM 模型与ABiLSTM 模型进行对比实验。

为了评价结果，使用了两个评价指标，分别为平均绝对误差mae 与R 平方R_square，计算公式如式（10）、式（11）所示。

平均绝对误差mae 是计算预测值与真实值偏差的绝对值大小，mae 值越小，表示模型预测效果越好。R平方是对模型拟合程度的打分，取值范围为［-1，1］。如式（11）所示，分子是预测值与真实值之间的误差，分母是真实值与目标值y的平均数之间的误差。由此可以得出，R平方的值越接近1，模型吻合程度越高。

实验结果如表1 所示。

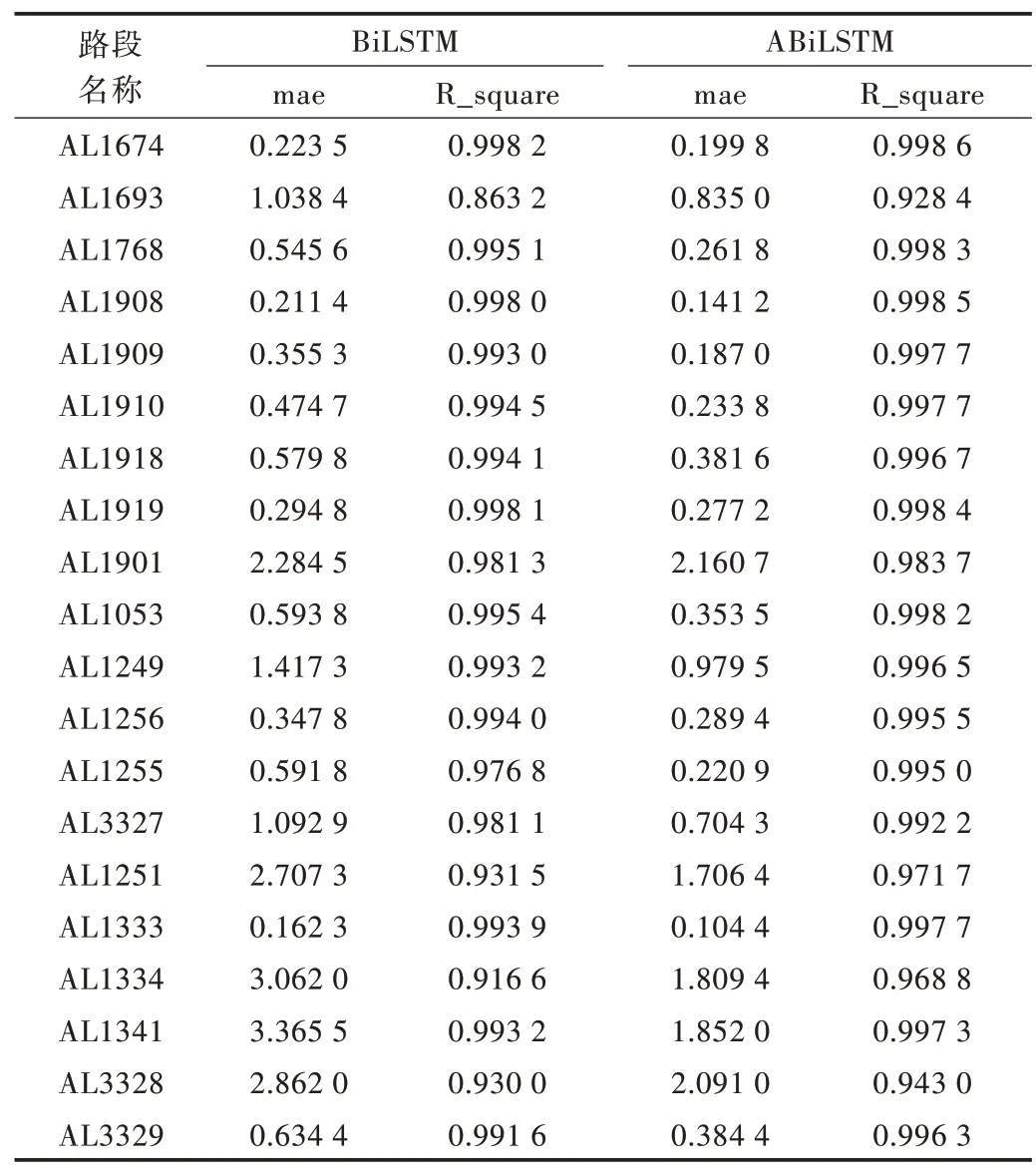
Table 1 Comparison of experimental results of ABiLSTM model表1 ABiLSTM 模型实验结果对比

两种模型在平均绝对值误差和R 平方上的对比结果如图2 所示。

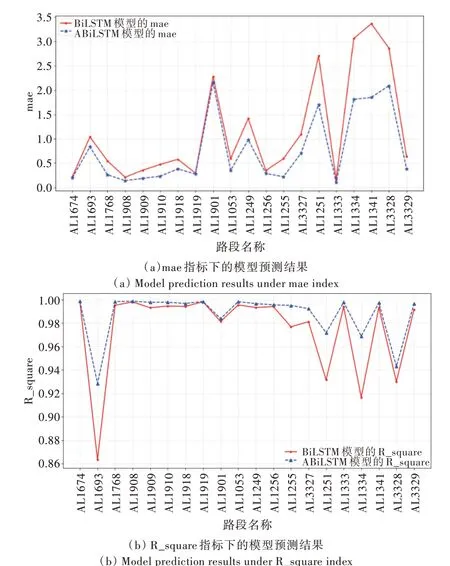
Fig.2 Comparison of experimental results of ABiLSTM model图2 ABiLSTM 模型实验结果对比

由表1 和图2 可以看出，ABiLSTM 在实验中的20 条路段上均表现出了更好的预测效果。

2 XGBoost 模型

极端梯度提升（eXtreme Gradient Boosting，XGBoost）模型是为了缓解单棵决策树可能造成过拟合的风险，对多棵决策树进行集成，从而使目标函数值不断下降［17］，具体表达式如式（12）所示。

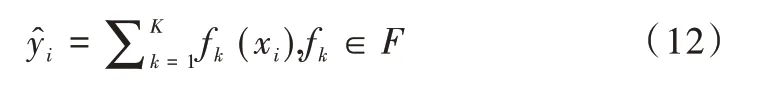
XGBoost 最核心的思路是每增加一棵决策树，整体表达效果都会有所提升，过程如式（13）所示。

在决策树中，叶子节点越多，造成过拟合的风险也就越大，所以需要限制叶子节点的个数，可以通过惩罚项实现，如式（14）所示。

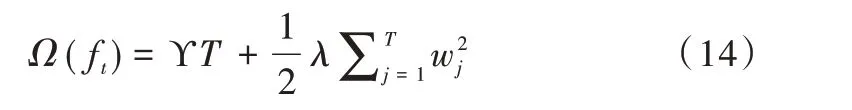
式（14）中，T为叶子节点个数，ϒ 为惩罚系数，表示惩罚力度的大小，w表示每个叶子节点的权重，表示对wj做了一次L2惩罚。

将损失函数与惩罚项相结合可以得到目标函数Obj(t)，接下来使用泰勒展开式处理目标函数，展开结果如式（15）所示。

对式（15）进行简化，为了便于合并，将惩罚项依据其定义进行展开，接着将样本上的遍历转化为叶子节点的遍历，最终结果如式（16）所示。

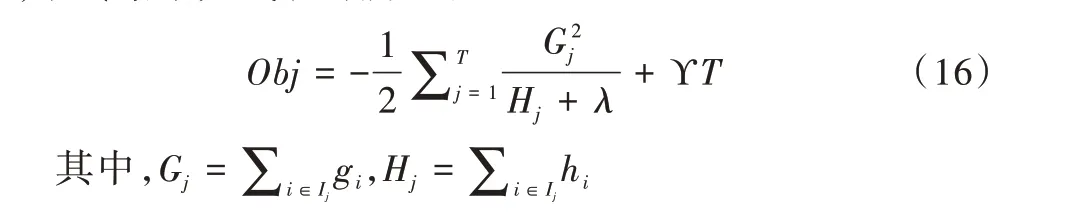
依据式（16），XGBoost 模型可以遍历不同决策树的划分方案，使得目标函数最小，即可以得到相较于上次决策树划分表现效果更好的模型。

2.1 hyperopt 方法自动调参

XGBoost 模型含有大量超参数需要设置，无论是采用手工调参方式还是采用网格搜索方式，都较为复杂，不利于模型优化，使用hyperopt 可以简化调参过程。hyperopt 有两种搜索算法，分别是随机搜索和TPE（Tree of Parzen Esti⁃mators）搜索［18］。本文使用的是TPE 搜索算法。

TPE 搜索算法相较于随机搜索在多数情况下表现出更好的效果。首先，采用随机搜索方式产生超参数，然后将这些超参数代入模型进行训练，通过目标函数值对参数进行评价。当随机产生的参数超过20 组时（默认为20），使用这些参数以及训练后模型的目标函数值产生无参数概率密度函数，然后使用概率密度函数生成新的超参数，对模型继续进行训练，直到产生相较于其它参数而言，具有较好表现效果的一组参数作为TPE 搜索算法的最终结果。TPE 搜索算法流程如图3 所示［18］。

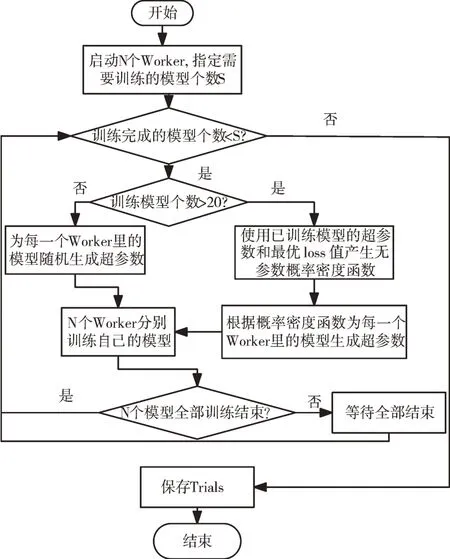
Fig.3 Workflow of hyperopt using TPE search algorithm图3 使用TPE 搜索算法的hyperopt 工作流程

hyperopt 是一个支持自动调参的python 库，在调参之前需要给出所要优化的目标函数及参数的搜索空间［18］。本文使用hyperopt 调参方式的参数搜索空间如表2 所示。

Table 2 Parameter search space of hyperopt method parameter adjustment表2 hyperopt 方法调参的参数搜索空间

以路段AL1053 为例，经过hyperopt 调参后XGBoost 模型参数如表3 所示。

Table 3 Super parameter values after adjusting parameters with hyperopt method表3 使用hyperopt 方法调参后的超参数取值

2.2 遗传算法调参

生物遗传时遵循分离规律及自由组合规律，变异时遵循重组规律、基因突变规律以及染色体变异规律。遗传算法（GA，Genetic Algorithm）受到生物进化学说和遗传学说的启发，模拟生物进化过程，借助复制、交换、变异等方法模仿生物优胜劣汰、适者生存的自然法则，具体而言就是在初始解的基础上通过智能式搜索逐步逼近最优解。相较于其它方法，遗传算法可以找到全局最优解［19］。

使用遗传算法解决具体问题时，需要根据问题的特性进行编码，确定适应度函数。该算法具有黑箱式结构，这使得可以用来研究一些函数关系不明确的复杂关系，如模型调参。

遗传算法具体可由以下遗传算子组成：

选择：计算个体适应度，然后从第t 代群体P（t）中选择出适应度较好的个体遗传到下一代群体P（t+1）中。使用轮盘赌法确定每一个体被选择的概率计算公式如式（17）—式（18）所示。

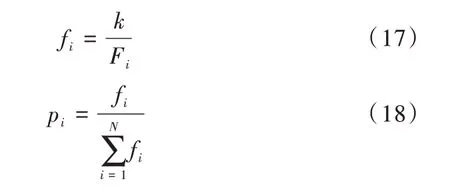
其中，Fi为个体i所对应的适应度函数值，N 代表现有的个体数。

交叉：将群体P（t）内的个体进行随机组合，选择确定的概率交换个体之间的部分染色体，产生新的个体。

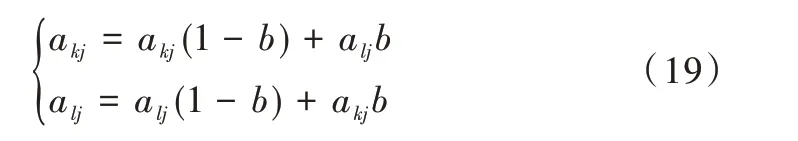
其中，b为取值在［0，1］的随机数。

变异：以某一概率将群体P（t）中的某些基因值替换为其它的等位基因［20］。表达式如式（20）—式（21）所示。

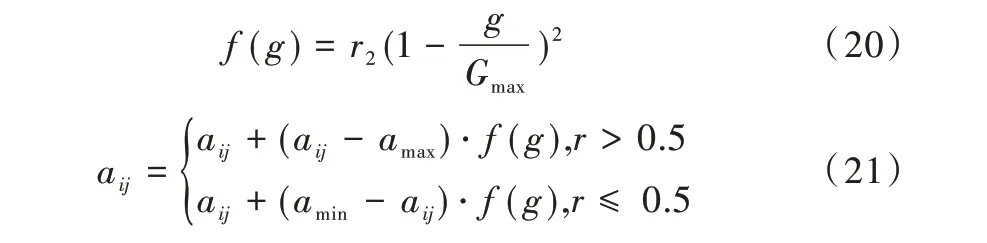
式（20）中，r2为随机数，g代表已经进化的次数，Gmax代表最终迭代次数。式（21）中，aij代表发生变异的第i个体的第j号基因，amax和amin分别代表该基因取值范围内的最大值和最小值，r是取值为［0，1］的随机数。

遗传算法运算过程如图4 所示。

Fig.4 Operation process of genetic algorithm图4 遗传算法运算过程

本文遗传算法中所使用的适应度函数为R 平方，表达式如式（11）所示。

利用遗传算法对XGBoost 模型进行调参，参数名称及参数搜索空间如表4 所示。

同样以路段AL1053 为例，显示经过遗传算法调参后XGBoost 模型的超参数如表5 所示。

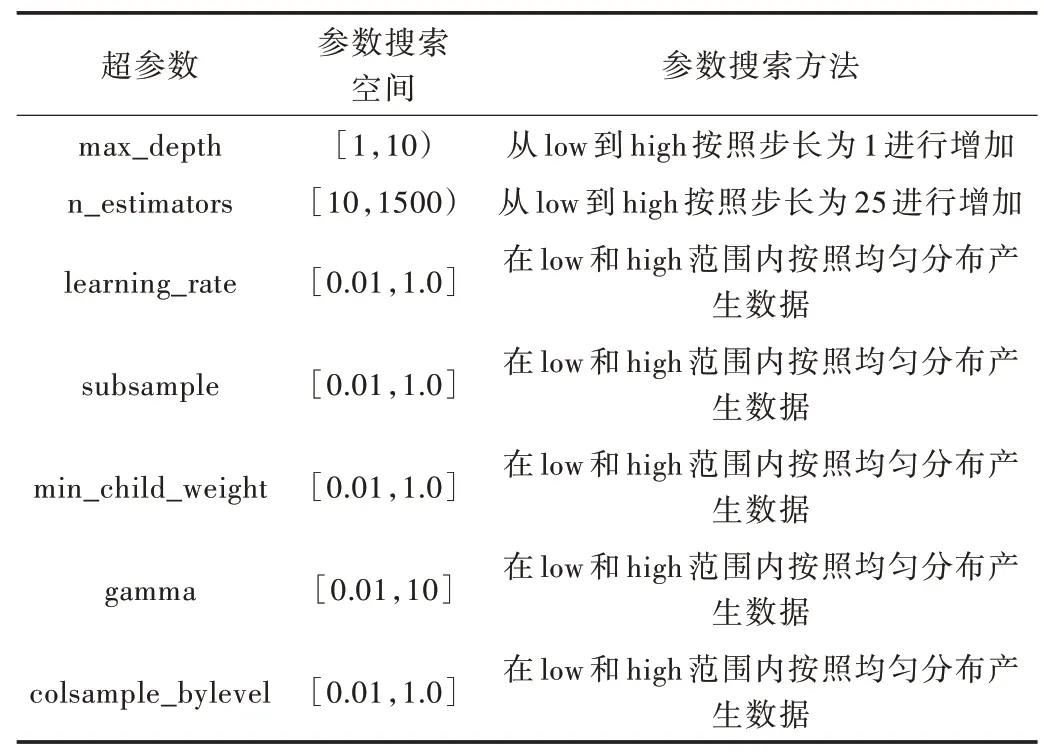
Table 4 Parameter search space of genetic algorithm parameter adjustment表4 遗传算法调参的参数搜索空间

Table 5 Super parameter values after parameter adjustment using genetic algorithm表5 使用遗传算法调参后的超参数取值

hyperopt 方法调参和遗传算法调参具有不同的特点，为了使组合模型具有最佳表现效果，本文对于每一条路的数据集都采用了两种调参方式，选择其中表现最好的模型与ABiLSTM 模型进行组合。

3 ABiLSTM与XGBoost组合模型

ABiLSTM 擅长于处理时序化数据，XGBoost 模型基于决策树对于回归和分类问题有较好的表现。两个模型结构相差较大，将两个模型进行组合可以降低过拟合风险，提高预测准确度。

使用残差表示模型预测结果的误差情况，残差计算如式（22）所示。

以路段AL1053为例，ABiLSTM 模型与XGBoost 模型前100个预测结果的残差结果如图5 所示。

Fig.5 Residual error of traffic time prediction图5 交通时间预测残差

由图5 可以看出，这两个模型预测结果的残差除在个别数据点有较大偏差外，其余数据点集中在［-1，1］，模型预测能力相差无几。在组合模型中，若两个模型的预测能力有较大差别，组合之后的结果往往差于两个模型中表现较好的模型。在本文实验中，单一模型BiLSTM 与XGBoost预测能力相近，通过将两个模型的预测结果进行组合，可以在一定程度上提高结果预测准确度。交通时间预测领域一些表现较好的组合模型多是基于时间序列方法与机器学习方法的组合，因为这两类模型的结构相差较大，可以减少过拟合程度，同时这两类模型具有不同特点，时间序列方法可以考虑周围时间段的结果对此刻的影响，可以提取到时间序列的隐藏特征，机器学习方法能够更加充分地挖掘属性间的依赖关系，将两类模型进行组合可以综合这两类模型的优点，表现出更好的预测效果。

3.1 误差倒排法

本文采用并列的模型组合方式，让每个模型单独训练，然后为每个模型的结果赋予不同的权重，让其共同决定组合模型的预测结果。模型组合的关键在于确定不同模型的权重，关于组合模型权重的确定方法，常见的有误差倒排法、等权组合预测法、方差—协方差法、最小二乘法以及最小绝对值法［21］。本文采用了误差倒排法和最小绝对值法分别进行试验。

误差倒排法的优点在于计算简便，同时考虑了不同模型之间预测效果的差异，在具有较好表现效果的同时，也具有很强的可解释性。使用误差倒排法组合模型的方法如式（23）—式（25）所示。

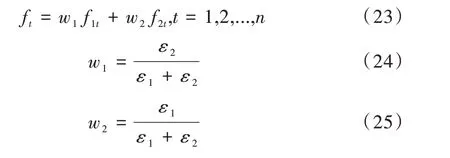
其中，ε1和ε2分别代表BiLSTM 与XGBoost 模型预测值与真实值之间的误差，w1与w2分别代表两个模型的权重。由权重计算公式可以看出，该方法考虑了不同模型间预测能力的差异，对于误差较小的模型赋予较大的权重，对误差较大模型赋予较小权重［13］，这样能够更好发挥组合模型的优势。

3.2 最小绝对值法

最小绝对值法相较于误差倒排法的优点在于可以为两个以上的单一模型确定权重参数，在一些复杂场景中，更具实用价值。最小绝对值法是将误差的绝对值作为目标函数，表达如式（26）所示［21］。

将预测结果记为矩阵A，真实值记为矩阵Y，权重记为W，表达式如式（27）所示。

其中，A的每一列表示一个模型所预测的n个数值，共有k个模型，表达式如式（28）所示。

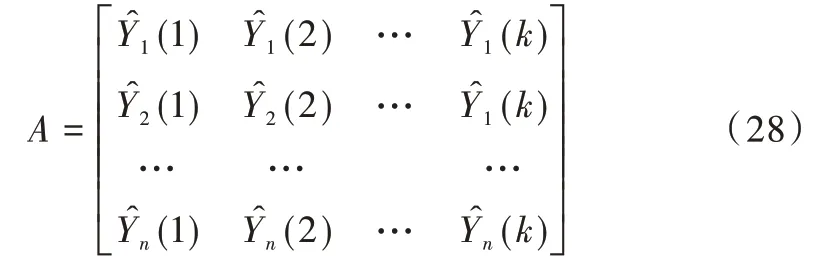
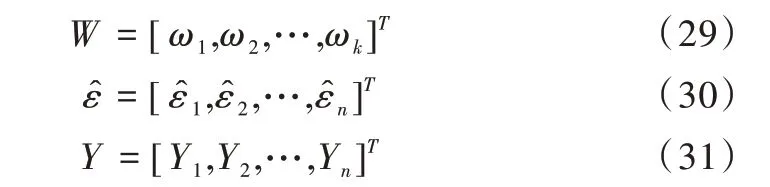
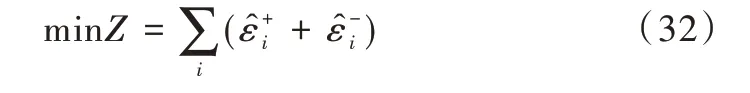
此时，该数学模型转化为一个典型的线性规划问题，可以使用单纯性法求解，矩阵表达式如式（33）所示。

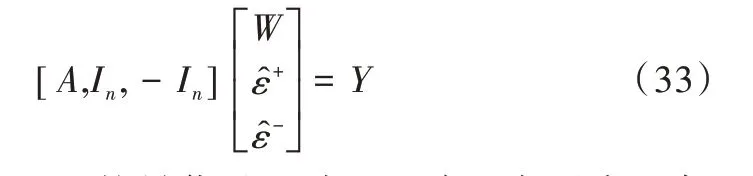
将矩阵[A,In,-In]的最优基记为B*，则B*在不失一般性条件下的表达式如式（34）所示。

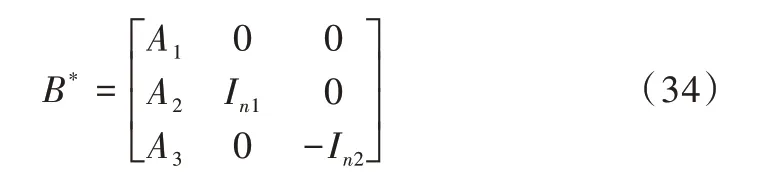
其中，W 为最终所要确定的权重系数。

4 实验结果及分析

本文将ABiLSTM 模型与经过调参之后的XGBoost 模型采用误差倒排法和最小绝对值法分别进行组合，实验数据为AL1674 等20 条路段在2014 年1 月份的交通数据，训练集与测试集划分比例为8∶2，采用随机划分方式。其中，XGBoost 模型使用了两种调参方式，选用表现效果最好的作为组合模型的一部分。表6 为单一模型及组合模型预测结果，使用的评价指标为均方误差mse，权重表示单一模型的预测结果在组合模型中所占比重。在20 条实验路段中，多数情况下，遗传算法调参表现出较好的效果，但在某些路段中hyperopt 自动调参表现出更好的效果，用*加以区分。

均方误差的计算公式如式（36）所示。

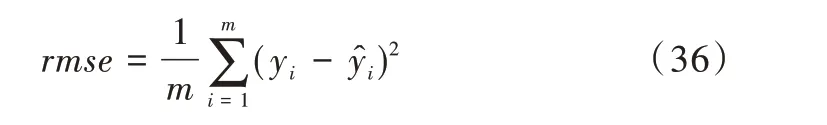
由表6 可以得出，使用误差倒排法确定的组合模型并非在所有路段上均优于单一模型，但使用最小绝对值法的组合模型相较于任何一个单一模型，均方误差都有所下降且表现出最好的预测效果。

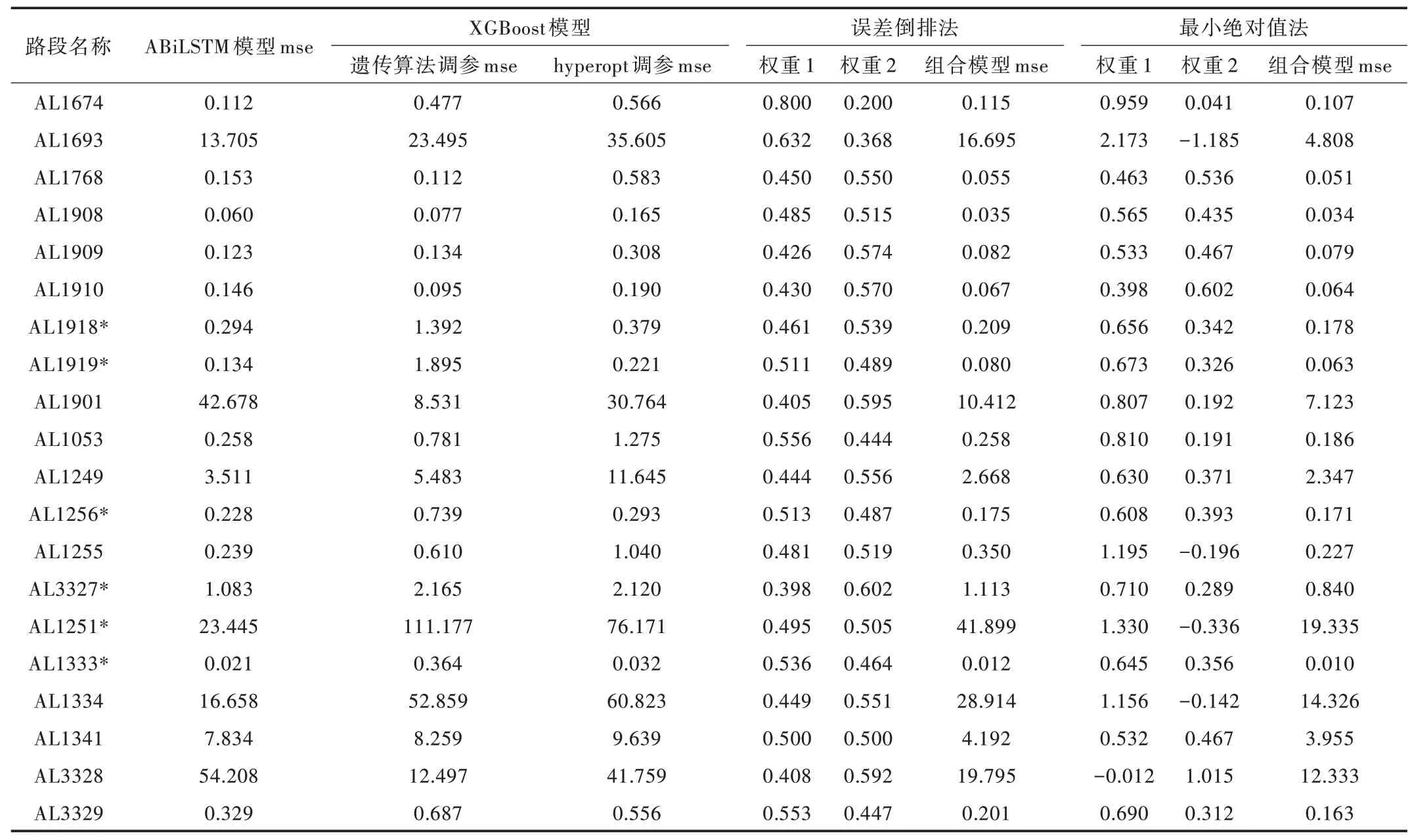
Table 6 Comparison of the prediction results of single model and combined model表6 单一模型与组合模型预测结果对比

为了显示组合模型在某条具体路段上预测值与真实值之间的偏差，以路段AL1053 为例，将组合模型的前100个预测结果与真实值显示在图中，如图6 所示。

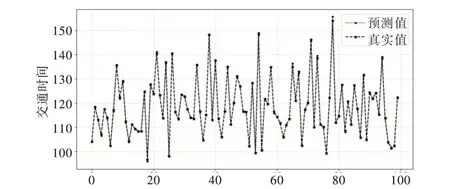
Fig.6 Predicted and actual traffic time of combined model图6 组合模型交通时间的预测值与实际值

由图6 可以得出，组合模型能够很好地拟合实际交通时间变化情况，具有较好的预测效果。

相对百分误差绝对值的平均值MAPE 可以用来评价模型的预测能力，MAPE 值越小，代表模型预测能力越强，计算如式（37）所示。为综合对比本文所提到的所有模型，现将不同模型在20 条实验路段上的MAPE 进行对比，结果如图7 所示。其中，“xgboost_Y”代表用遗传算法进行调参的XGBoost 模型，“xgboost_H”代表用hyperopt 方法自动调参的XGBoost 模型，组合1 代表用误差倒排法确定权重的组合模型，组合2 代表用最小绝对值法确定权重的组合模型。

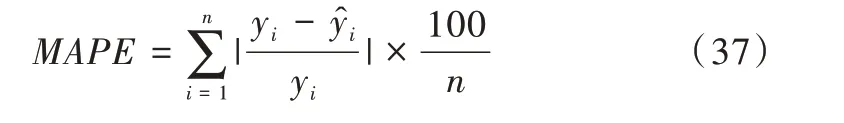
Fig.7 Comparison of broken lines of different models of MAPE图7 不同模型MAPE 的折线对比

由图7 可以看出，未添加注意力机制的BiLSTM 模型的预测能力相较于其它模型表现较差，添加了注意力机制之后，使得MAPE 指标有较大程度的下降，模型预测能力有较为明显的提高。并且，利用了不同调参方式进行调参的XGBoost 模型的MAPE 指标相近。两种组合模型在多数路段上表现优于其它单一模型，但在路段AL1693 上，使用误差倒排法确定权重的组合模型表现差于任何一个单一模型。综合而言，使用最小绝对值法确定权重的组合模型预测能力优于任何一个单一模型，在所有模型中表现最优。

箱线图可以用来反映一组数据的中心位置和散布情况，为了更直观统计不同模型在所有实验路段上MAPE 指标的离散情况，现将不同模型在所有实验路段上的MAPE指标绘制为箱线图，如图8 所示。

Fig.8 Comparison of MAPE box lines of different models图8 不同模型MAPE 箱线图对比

由图8 可以得出，两种组合模型MAPE 指标的中位数低于其它所有模型，但组合2 即使用最小绝对值法确定权重的组合模型，相较于使用误差倒排法确定权重的组合模型，其MAPE 指标更为集中，上四分位数和上边缘也更低，使用最小绝对值法确定权重的组合模型的异常值数量及取值也均小于使用误差倒排法确定权重的组合模型。综上所述，使用最小绝对值法确定权重的组合模型在所有模型中表现出最好的预测效果。

通过表6、图7 及图8 可以得出，本文提出的使用最小绝对值法确定权重的组合模型在不同指标评价下，表现均优于其它任何模型，从而说明ABiLSTM 与XGBoost 组合模型可以提高单一模型预测准确度。

5 结语

本文将BiLSTM 模型与注意力机制相结合，对BiLSTM模型进行了改进。通过实验证明，该模型相较于BiLSTM模型表现出更好的预测效果。XGBoost 模型具有大量参数，本文尝试了两种不同的调参方法，即遗传算法调参和hyperopt 自动调参，为确定组合模型的权重，使用误差倒排法和最小绝对值法分别进行实验，选取表现更好的最小绝对值法为不同模型确定权重系数，进而将模型进行组合。通过实验证明，该组合模型较任何单一模型都表现出更好的预测效果。本文所使用的数据集考虑了时间相关性，但未考虑到空间相关性。现实生活中，一条路段的通行情况不仅与它相邻时间段的路况有关，还与相邻路段的通行情况有关。因此，下一步还应使用时空数据进行实验，更加全面地考虑影响交通时间的各种因素，从而提高交通时间预测准确性。