滚动轴承故障的卷积神经网络诊断研究

王 丹，金光灿，邱 志，邢彦锋

（1.上海工程技术大学 机械与汽车工程学院，上海 201620；2.舍弗勒贸易（上海）有限公司，上海 201804）

0 引言

轴承故障诊断一直以来都是学者研究和工程应用的重点，轴承对于旋转机械设备起着至关重要的作用。传统基于振动理论的轴承故障诊断有很多方法，如奇异值分解［1］、经验模态分解［2］、包络谱分析［3］、谱峭度法［4］等，这些方法不仅依赖于诊断者的理论知识储备，在数据预处理阶段也需要耗费较长时间。

机器学习作为人工智能领域极具影响力的学科之一，在轴承故障诊断方面提供了很多可行性方案。支持向量机与随机森林作为机器学习的常用方法被用于轴承故障诊断［5-6］。然而，传统的机器学习通常需要人工构造特征，并把特征映射到目标空间，降低了使用的便捷性。2006年，Hinton 等［7］提出深度学习理论，由此掀起了深度学习的研究热潮。其中，卷积神经网络（Convolution Neural Net⁃work，CNN）算法因其在特征学习和模式识别方面具有良好效果，常被应用于语音识别、图像处理和目标检测等［8］。如葛程等［9］利用卷积神经网络进行图像分类研究，刘斌等［10］利用神经网络进行汽轮机发电机组故障诊断。深度学习避免了人工提取特征的弊端，在轴承故障诊断领域也得到了广泛应用。部分学者针对以时域一维信号作为卷积神经网络输入的轴承故障诊断进行了许多研究，并取得了一定成果［11-16］。如李恒等［17］直接对振动信号进行短时傅里叶变换（Short-Time Fourier Transform，STFT），以时频谱作为卷积神经网络的输入；肖雄等［18］将一维信号转换为二维灰度图，利用二维卷积神经网络进行轴承诊断；袁建虎等［19］和Kumar 等［20］则对振动信号连续小波变换得到的时频谱进行卷积神经网络深度学习。以上研究在采用卷积神经网络进行故障诊断时大多能获得较高的准确率，但是部分研究在对原始信号进行预处理时，常常会损失一些特征信息，导致深度学习最终识别准确率未能达到100%。所以在确定卷积神经网络输入层的数据集时，应考虑输入特征信息的完整性，以保证最终的预测准确率，并且要尽可能降低数据预处理难度。

为尽可能保留故障特征信息，需要寻找更合适的数据预处理方法，以提高卷积神经网络的识别准确率。因此，本文提出基于短时倒频谱变换（Short-Time Cepstrum Trans⁃form，STCT）与卷积神经网络的轴承故障诊断方法。将包含振动信号故障特征的二维倒频谱作为卷积神经网络的输入，利用卷积神经网络的自适应提取，深度挖掘与学习原始信号故障特征，针对正常和不同转速、不同破坏程度的轴承外圈与内圈作故障诊断研究。实验结果证明，该方法对于轴承故障具有很高的识别准确率。

1 短时倒频谱

倒频谱是对功率谱求对数后作傅里叶逆变换后得到的，相较于功率谱，倒频谱可以消除传递通道的影响，即传感器布置位置引起的振动传递路径差异。短时倒频谱变换是将一维倒频谱转换成包含倒频率和时间序列的二维倒频谱，其思想是利用窗函数对截取后的时域信号作倒频谱计算，通过窗函数的移动实现最终的倒频谱集合。

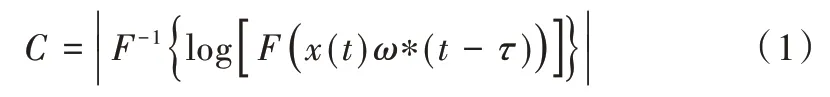
式中，x（t）为振动信号，ω*（t-τ）为窗函数，F为傅里叶变换，F-1为傅里叶逆变换，C为倒频谱幅值。

式中，q为倒频率，L（ω）为窗函数长度，fs为采样频率。倒频率q即为对应频率的倒数，实际应用中应考虑倒频率包含的故障频率范围。

2 卷积神经网络

卷积神经网络作为深度学习的代表方法之一，在表征学习方面具有较多优势。卷积神经网络的三大特点是局部连接、权值共享和下采样。一个典型的卷积神经网络主要由输入层、特征提取层、分类层和输出层组成。其中，特征提取层主要包括卷积层、池化层、激活函数和批归一化处理；分类层主要包括全连接层以及用于分类的激活函数。

3 实验验证

3.1 数据集描述

为验证本文提出故障诊断方法的有效性，并构建数据集，现以NU218 圆柱滚子轴承为例，人为破坏轴承内外圈，搭建实验台测得其在不同转速下的振动信号。实验时设置径向载荷为10KN，采样频率为25.6KHz。共设置11 组不同的轴承状态，为保证模型的鲁棒性，针对每种状态均加入3 种转速下的数据样本。每种转速的样本数为400，共计13 200 个样本。其中，随机选择10 560 个样本作为训练集。详细的实验样本组合如表1 所示。

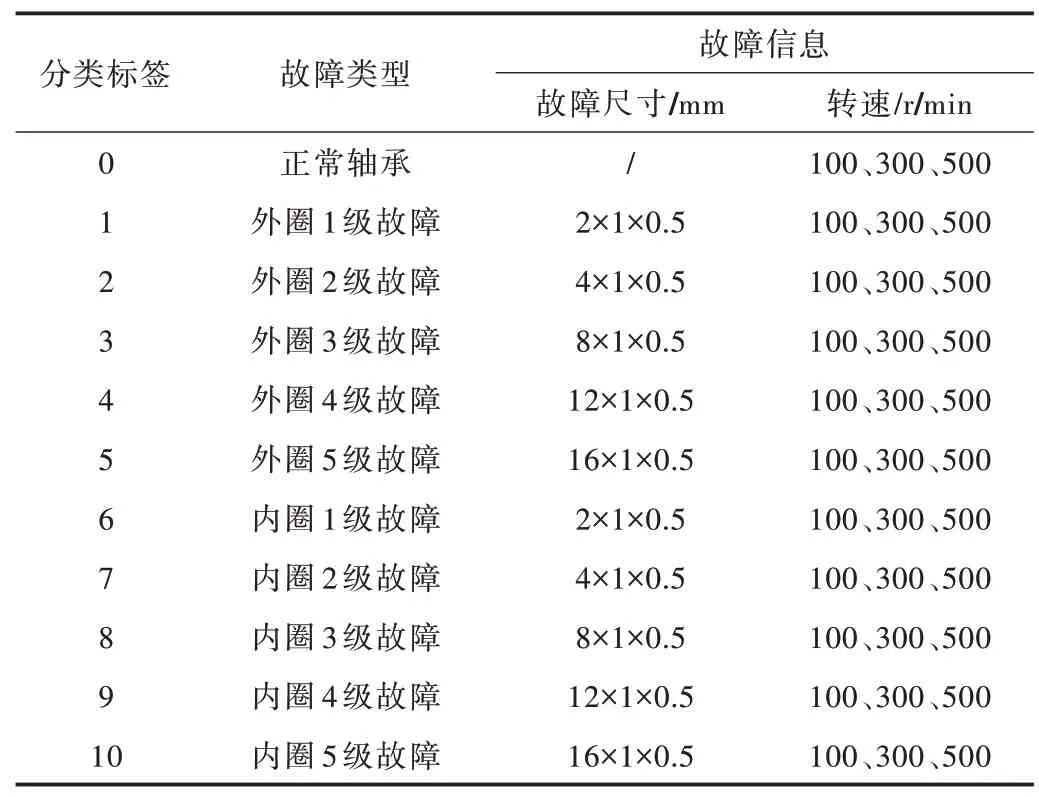
Table 1 Experimental data set表1 实验数据集

图1给出轴承在500r/min 转速下外圈5级故障的短时倒频谱，在该转速下，轴承外圈的理论故障频率为60.152 5Hz，理论倒频率为0.016 6s。从图1（a）中可看到明显的谱峰亮带，根据图1（b），X 轴为时间，Y 轴为倒频率，Z 轴为倒频谱幅值。此处的倒频率对应轴承外圈在500r/min 转速下的故障频率。

图2（a）给出了轴承在100r/min转速下外圈1级故障的短时倒频谱，在该转速下，外圈的理论故障频率为12.030 5Hz，理论倒频率为0.083 1s。从图2（b）中可以看出，外圈的倒频率被周围谱线掩盖，此时无法提取故障特征。因此，在低转速的工况下，仅通过倒频谱无法直接作出故障诊断。

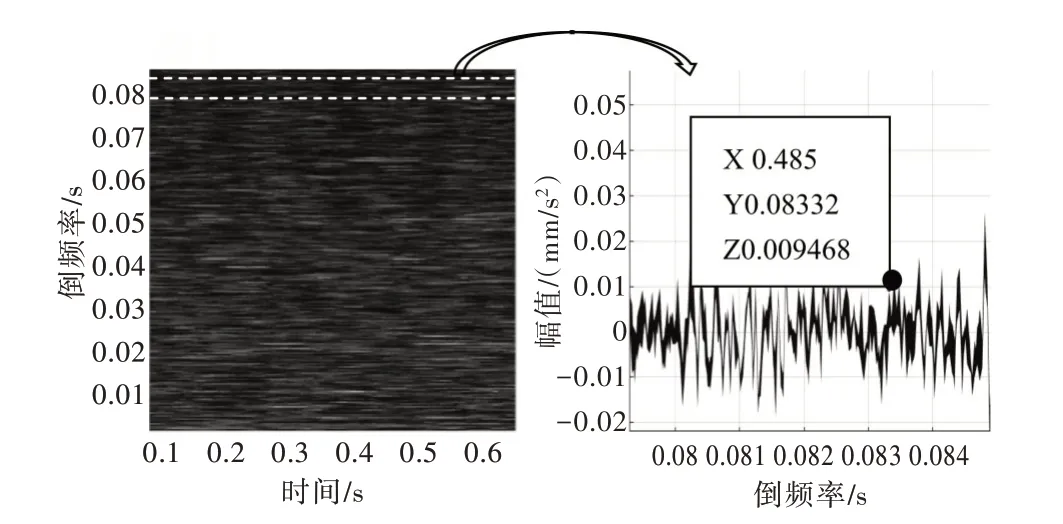
Fig.1 Short-time cepstrum of order 5 fault in outer ring at 500r/min图1 500r/min 转速下外圈5 级故障的短时倒频谱

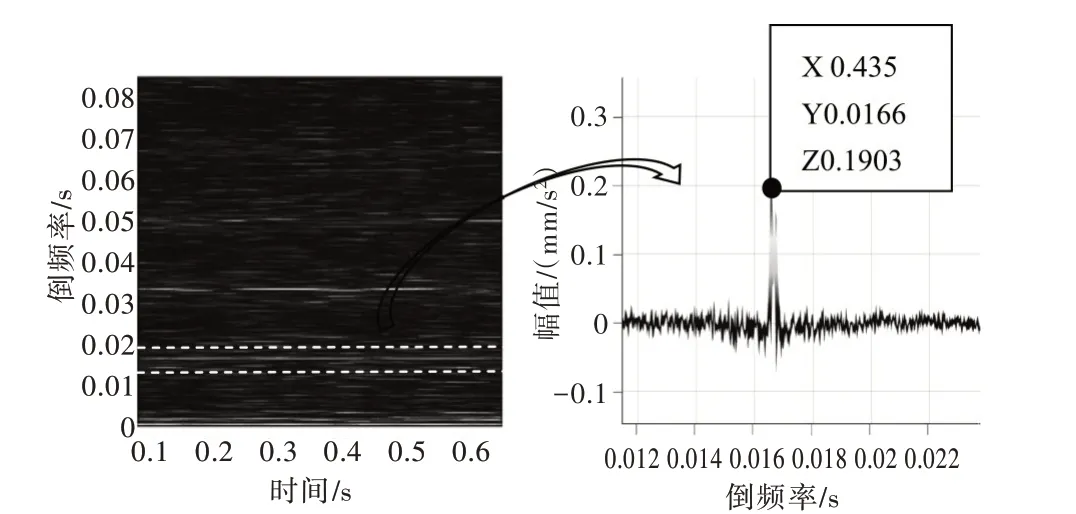
Fig.2 Short-time cepstrum of order 1 fault in outer ring at 100r/min图2 100r/min 转速下外圈1 级故障的短时倒频谱

3.2 模型建立

3.2.1 图像输入

根据3.1 节所述生成对应数量的短时倒频谱，为突显图片特征并提升训练效率，本文先对图片进行二值化处理，再将像素调整为200×200。

3.2.2 卷积神经网络结构

由于目前尚无理论性的卷积神经网络结构建立方法，本文在参考已有文献的卷积神经网络结构基础上，探索适合本文的模型参数。以优化器、学习率和学习回合数（ep⁃och）作为卷积神经网络训练时的主要参数，在此引入正交实验确定这些参数的最佳组合。表2 给出相应正交实验的水平因素表，表3 则为正交实验方案及结果分析。

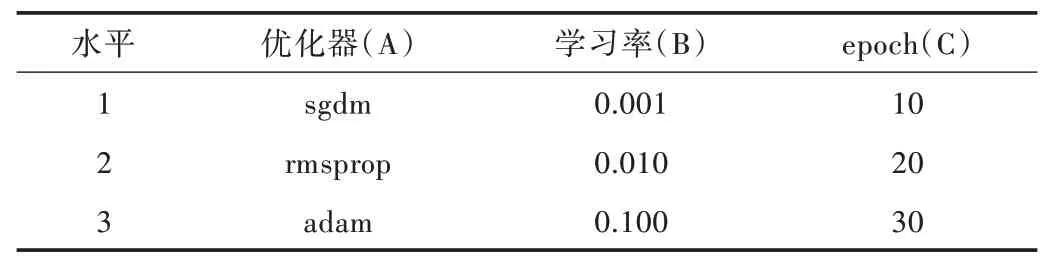
Table 2 Horizontal table of orthogonal test factors表2 正交实验因素水平表

在表3 中，以训练结束时的准确率和训练完成时间作为评价指标，每组实验方案进行10 次，取平均值。根据实验结果可得：对于因素A，3 个水平对应时间相差不大，故选择准确率最高的A1；对于因素B，3 个水平对应时间也相差不大，故选择准确率最高的B1；对于因素C，水平1 对应时间相比其它两个水平明显较短，且对应准确率也较高，故选择C1，最终得到的最优组合为A1B1C1。卷积神经网络架构如表4 所示。

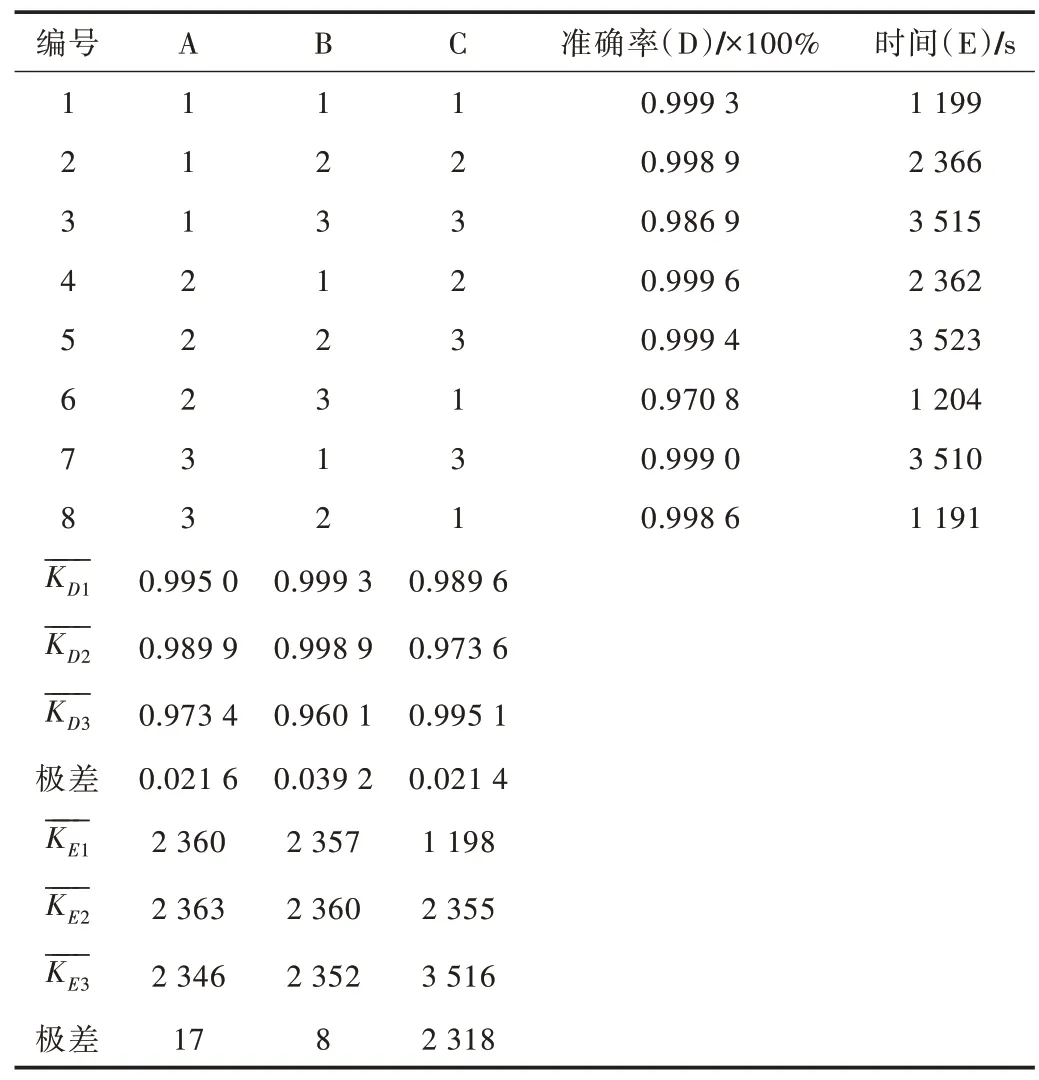
Table 3 Orthogonal test program and result analysis表3 正交实验方案及结果分析

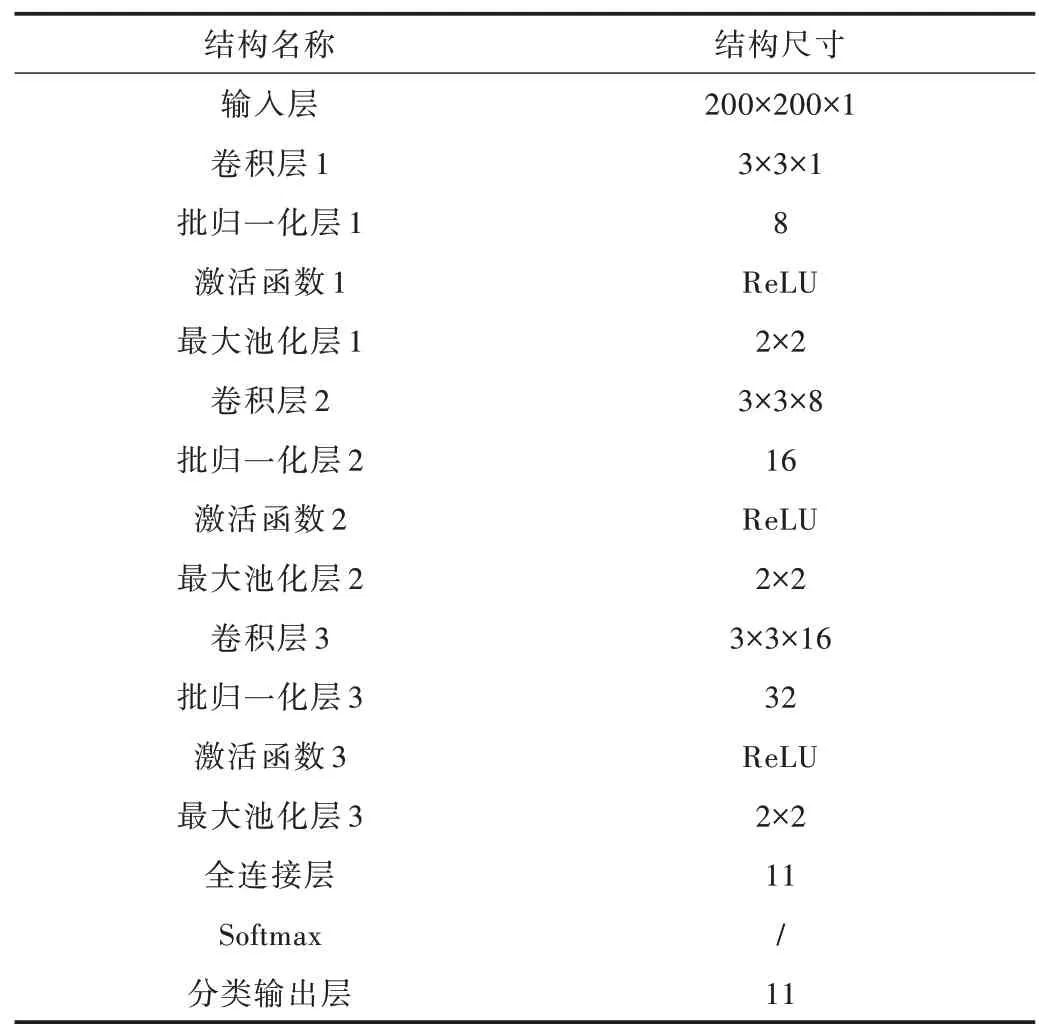
Table 4 Convolutional neural network architecture表4 卷积神经网络架构

训练过程如图3 所示。从图中可以看出在前两个训练回合中，训练的准确率迅速提升，并在之后的训练中保持缓慢增长，最终的训练准确率为99.92%，用时20min40s。

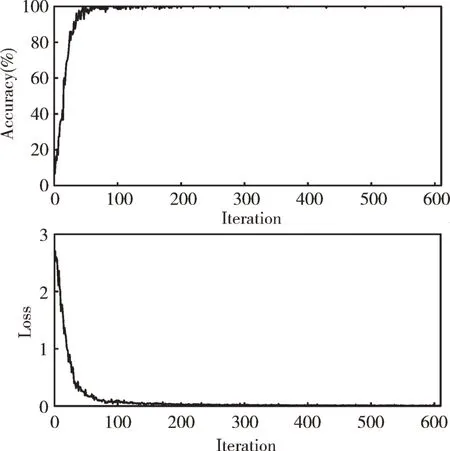
Fig.3 Training process图3 训练过程

3.3 结果对比分析

采用3.2 节训练的卷积神经网络对测试集进行测试。将测试集分成4 类，分别为只包含100r/min、300r/min、500r/min 单个转速下的轴承故障数据测试集和包含3 种转速的轴承故障数据测试集。同时，采用短时傅里叶变换以及将时域信号转换为二维图像两种不同方式对原始数据进行预处理，并将预处理后的数据集作为卷积神经网络的输入。图4 给出在100r/min 转速下对原始信号进行短时倒频谱变换作为卷积神经网络输入的测试结果混淆矩阵图。混淆矩阵X 轴表示实际分类的标签，Y 轴表示经卷积神经网络测试后预测的分类标签。混淆矩阵对角线上的数值为正确分类的图片数，其余位置数值表示该点对应Y 轴标签被错误分类为对应X 轴标签的图片数。

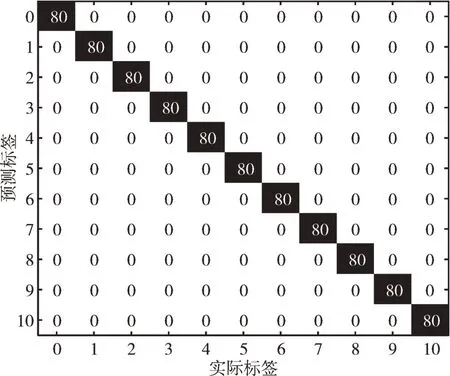
Fig.4 Confusion matrix diagram of test results for short-time cepstrum transform图4 短时倒频谱变换测试结果混淆矩阵

采用上述3 种数据预处理方法所得的测试结果如表5所示。

由表5 可知，在直接应用时域信号作为卷积神经网络的输入时，由于原始信号受噪声、转速等影响，特征信息被掩盖，不易得到准确的训练结果和测试结果，尤其在低转速工况下。在对原始信号作短时傅里叶变换后，将其作为输入，由于在不同工况下谱峰有相同部分，会产生一定几率的误判，由测试结果可知，虽然准确率已达到99%以上，但仍存在误判的情况。相比之下，采用原始信号的短时倒频谱变换作为输入对信号进行故障特征预提取，保留了更多细节特征，在单一转速和多种转速混合的情况下，测试准确率均能达到100%。

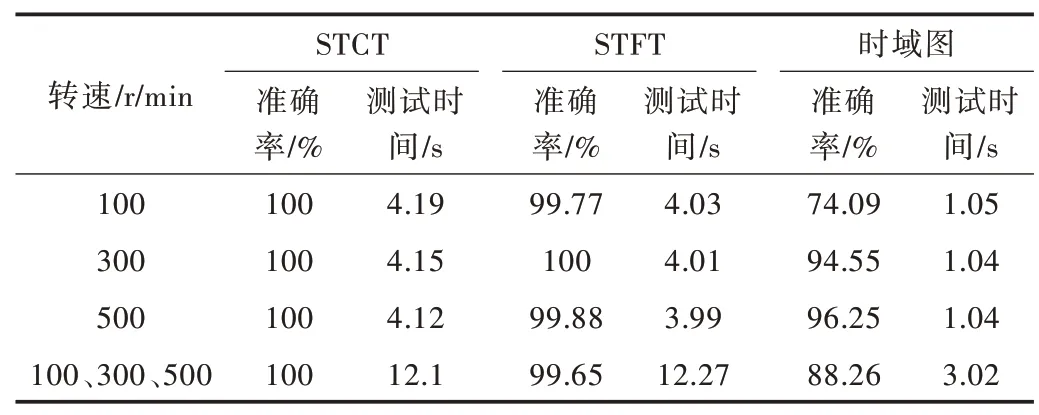
Table 5 Final test accuracy of different signal processing methods表5 不同信号处理方法的最终测试准确率

4 结语

本文提出基于短时倒频谱与卷积神经网络的滚动轴承故障诊断方法。首先，对信号作短时倒频谱变换，将一维信号转换为二维倒频谱作为卷积神经网络的输入；然后，采用正交实验进行卷积神经网络参数选优；最后，在最优参数的基础上对预先构建的数据集进行训练与测试。无论是在一种转速还是多种转速混合情况下，都能对滚动轴承故障进行准确诊断。通过该研究，倒频谱变换在引入窗函数后，实现了一维到二维的转变，使其应用范围更广，且这种预提取故障特征的方式为智能诊断提供了参考。在应用卷积神经网络后，轴承的故障诊断不再局限于基于传统信号处理方式通过优化方法进行神经网络参数选优，从而避免盲目选参的问题。但目前仅考虑了转速不变的情况，在大多数工况中，转速往往是变化的，接下来应针对变转速、强噪声情况下的滚动轴承故障诊断进行研究。