融合深度学习模型的时序网络重要节点识别方法研究

黄 娟，郭 强，刘建国

（1.上海理工大学 管理学院，上海 200093；2.上海财经大学 金融科技研究院，上海 200433）

0 引言

相比于传统静态网络，时序网络不仅能够表示节点间的关系，还能通过节点或连边的增加或减少表现拓扑结构随时间变化情况，近年来被广泛应用于建模解决金融、医疗、交通、电子商务等领域问题［1］。关键节点是整个网络中处于核心位置的节点，对整个网络的结构和功能具有较大影响力。在时序网络中，识别关键节点能够更精准地刻画事物间的交互关系及发展进程，如建模复杂社交系统、刻画经济网络、建立合作网络、预测重要枢纽以防止交通堵塞、预测关键患者以防止病毒传播、识别核心客户、预测流行产品等［2-5］。因此，研究并设计有效的关键节点识别方法具有重要的理论与实践意义。

近年来，时序网络中关键节点的识别方法大致可分为3类：基于拓扑结构的识别方法、基于动力学的识别方法，以及基于机器学习的识别方法［1］。其中，经典的时序网络关键节点识别研究工作主要思路在于根据时序数据构建时序网络模型，通过网络的拓扑结构或动力学特征，采用节点排序算法识别网络中的关键节点。基于拓扑结构的识别方法仅考虑时序网络每个层内的连接关系，为更好地表示时序网络的时序特征，还需要考虑不同时间层间的连接关系［6-7］。如Taylor 等［8］在传统动力学方法的基础上，采用多层耦合网络分析方法，将时序网络按照层间关系和层内关系建立超邻接矩阵（Supra-Adjacency Matrix，SAM），然后根据特征向量的中心性得到节点重要性排名；杨剑楠等［6］在SAM 方法的基础上，通过邻居拓扑重叠系数构建新的超邻接矩阵（Super Supra-Adjacency Matrix，SSAM）。以上学者的研究结果表明，对层间关系的建模能更准确地预测节点的重要性排序。此外，机器学习结合复杂网络的研究也得到学者们的广泛关注，如林国强等［9］将复杂网络分析数据作为特征输入机器学习模型，用支持向量机方法预测P2P行业的用户违约情况；Fang 等［10］以时间T 为界限，以在此之前的数据作为训练数据，剩余数据作为测试数据，并以社会网络理论为依据选取相关特征，采用决策树模型训练并预测社会网络中最有力的说服者。以上学者成功将时序信息引入到机器学习方法中，从而为后续相关研究提供参考。

综上可以看出，近年来基于动力学的研究主要在于充分运用时序网络中的层间信息辅助关键节点识别。基于机器学习方法的识别研究工作尝试更好地将时序信息引入到模型中，但这些方法仅从单一角度进行分析，每种方法往往都优缺点并存，加上时序网络中不同时间段的数据特征并非完全一致，很难突破现有瓶颈以及获得更高的准确率。因此，本文结合上述两种分析角度，提出一种基于深度学习的混合预测模型，使得两种方法在有效发挥优势的同时，优缺点也可以实现互补。首先，深度学习模型和SSAM 方法分别独立地预测节点重要性排序，然后通过训练一个线性模型对两种方法得出的结果进行加权处理，从而确定最终的节点排序。

1 相关研究

1.1 SSAM 识别方法

时序网络可按照一定时间间隔被切分为T个时间窗口，则其可被分为有序的时间层网络G1,G2,G3,…GT。时序网络可被超邻接矩阵建模表示，SSAM 方法采用一个NT×NT的分块矩阵建模时序网络。具体形式如下：

其中，A(1),A(2),A(3),…,A(T)均为N×N的邻接矩阵，用于表示各网络层的层内连接关系，C(1,2),C(2,3),…,C(t-1,t)均为由邻居拓扑重叠系数组成的N×N对角矩阵，用于表示各网络时间层之间的层间连接关系。其定义为：

之后，SSAM 方法针对上文中的超邻接矩阵A'计算主特征向量v={v1,v2,…,vNT}，其中wit=vN(t-1)+i即为时间网络层Gt中节点i的特征向量中心性，其作为节点重要性排序的衡量指标，可得出每个时间网络层上的节点重要性排序［6］。

1.2 长短期记忆神经网络

长短期记忆神经网络（Long Short-Term Memory Neural Network，LSTM）是循环神经网络的一个变种，其在基础循环神经网络单元基础上增加了记忆和遗忘单元，使之能更有效地处理与预测较长的时间序列数据［11-12］。LSTM 通过门控制结构调控先前与当前时间单元的信息，输入门it、遗忘门ft和输出门ot将短期记忆与长期记忆结合起来，使循环神经网络具备长期记忆能力［10］。LSTM 工作流程可表示为：

（1）遗忘门ft对信息进行过滤，通过Sigmoid(σ)函数使有用信息的值接近1；反之，无用信息的值接近0。

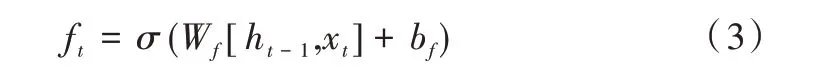
（2）输入门根据当前输入信息和遗忘门的结果更新状态信息：

输入信息：

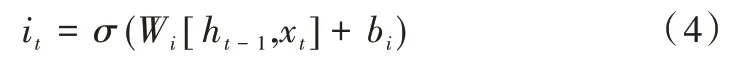
记忆细胞：

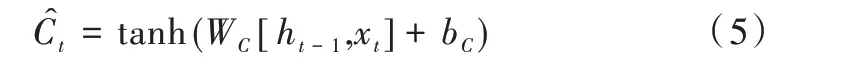
长期记忆细胞：

（3）输出门输出信息：

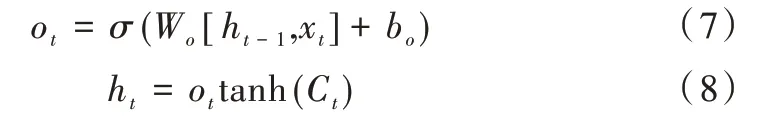
其中，σ代表Sigmoid函数，W、b分别代表各个门单元中的权重和偏置，ht-1、ht分别为前序和当前时间单元的输出信息，xt为当前时间单元的输入信息。基于循环神经网络结构的LSTM 能有效利用前序时间单元上的信息，已被广泛应用于时序数据预测任务，因此本文采用LSTM 模型结构对时序网络数据进行处理与预测。

2 基于深度学习的混合预测模型

2.1 混合模型结构

本文从模型融合角度出发，结合SSAM 方法与LSTM 模型优势，使二者的优劣势互补，从而提高时序网络中节点重要性排序的预测准确率。本文提出的混合模型可分为3部分：SSAM 模型、LSTM 模型和线性加权模型。

在第1 部分中，本文在SSAM 模型部分主要参考并复现杨剑楠等［6］的研究工作，首先通过超邻接矩阵建模时序网络，之后根据节点的特征向量中心性得出每个时间层网络上的节点重要性排序。

第2 部分为基于LSTM 的时序预测模型，由循环神经网络LSTM 与一个全连接网络层（Fully Connected Layer）组成。首先，LSTM 方法根据先前与当前信息输出节点的向量化表示；其次，将这些向量作为特征输入分类器，分类器根据节点特征将其分类为对应排序区间。

以上两部分在混合模型中可并行化地执行，其结果互不干扰，两者分别独立预测节点在每个时间层网络上的排序，但往往由于数据特征以及方法本身的限制，单一方法难以取得更好的预测效果。因此，本文在混合模型的第3部分采用融合的方式，使用一个线性模型加权两种方法得出节点排序，最终的排序结果无需人为干涉，线性模型能够自动学习不同时间层上的加权权重。图1 描述了混合模型基本组织架构。

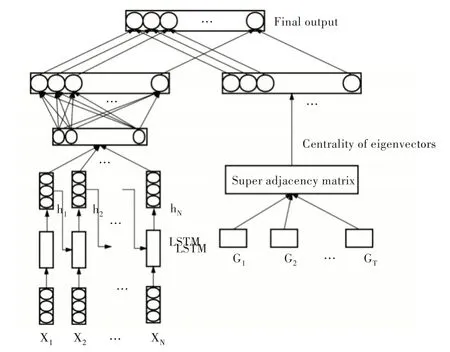
Fig.1 Basic architecture of hybrid model integrating deep learning model图1 融合深度学习模型的混合模型基本组织架构

混合模型的基本训练流程如下：

算法：模型训练流程描述

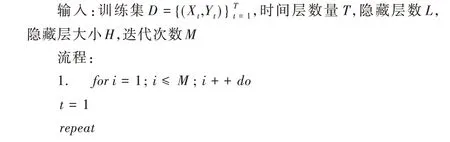
2.2 模型训练策略

为了验证模型预测的准确率及参数设置的合理性，并避免因数据随机切分等带来的干扰，本文在模型训练与验证过程中采用K折交叉验证法，即将数据划分为K份，训练总共进行K轮次，每次使用其中1 份用于验证模型效果，剩余K-1 份用于训练模型，并以K次实验结果的均值作为最终结论。根据时序网络数据特征，本文分别按照基于时间与基于节点的切分方式划分数据集，用于适应不同的数据集及进行实验对比。则上述两种数据切分方法可被描述为：

（1）基于时间的数据切分。时序网络按照时间窗口划分。假设时间总周期为10，K值取5，则每轮次训练时选取连续的2 个时间窗口作为验证数据，剩余8 个连续时间窗口作为训练数据。

（2）基于节点的数据切分。时序网络首先按照时间窗口划分，之后训练和验证数据再按照节点划分。假设K值取5，则每轮次训练时选取20%的节点作为验证数据，其余80%的节点作为训练数据。

3 实验及结果分析

3.1 数据描述

本文使用Workspace 数据集进行模型训练与测试，该数据集包括法国某公司通过移动射频技术采集的员工之间面对面交互产生的交互数据，持续时间为2013 年6 月24日-2013 年7 月3 日，并按照天为单位进行切分。表1 描述了该数据集的基本统计特征，其中N为网络中的节点总数，C为总交互次数，E为连边数目，T为时间窗口数量。

Table 1 Workspace dataset statistics description表1 Workspace 数据集统计描述

3.2 标签及评价指标

节点在网络中的重要性排序可根据删除该节点前后网络的连通性变化进行度量，如果节点删除后网络的连通性变化较大，则证明被删除的节点对于网络较为关键，反之则重要性较低［1，6-7］。网络的连通性可由网络的时序全局效率来表示，其定义形式如下：

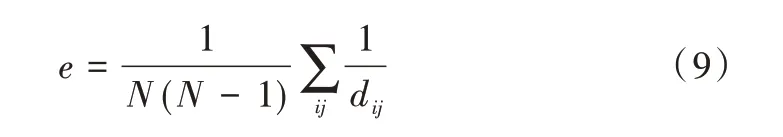
其中，N为网络中的节点数量，dij表示网络中各节点间的时序距离。定义eit为时间层网络Gt在删除了节点i 之后的时序全局效率，则该节点的重要性排序依据可表示为：

Eit值越大，则该节点在网络Gt中的排序越靠前。本文将通过节点删除法得到的节点重要性排序作为模型训练中的标签值。此外，为降低分类模型的复杂度，本文将节点排名作近似处理，如将12、18 分别转变为10 和20，该处理方式使得模型由92 分类问题降为10 分类问题。

为了检验实验得出的节点重要性排序效果，本文采用肯德尔系数（Kendall's τ）作为评价指标。Kendall's τ是度量两个有序序列之间相关程度的常用方法，其取值范围为[-1,1]。该值越大，证明两个序列相关性越强。两个序列越相似，当其数值大于0 时，可作为关键节点的识别准确率［6-8］。对于序列{a1,a2,…,an} 和序列{b1,b2,…,bn}，Kendall'sτ可定义为：

3.3 实验结果比较

为了使LSTM 方法能够更好地在当前时间层网络表示节点属性，本文参考网络拓扑结构中的主要特性，采用Pearson 相关系数过滤法过滤掉与节点排名相关性过低的特征（绝对值小于0.2）。将所选取的特征作为输入，通过LSTM 方法构建每个节点的向量化表示。

最终，本文按照上述特征选取方法选取如下节点拓扑属性作为输入特征：节点入度、节点出度、节点度、接近中心性、介数中心性、特征向量中心性以及连边介数中心性共7 个特征。所选取的特征间的相关性如图2 所示（彩图扫OSID 码可见，下同）。

由图中可以看出，节点度数、接近中心性及介数中心性3 个拓扑特征与节点重要性排名有较高相关度，说明这些特征将在预测中起关键作用。以上特征数值高的节点，在排序中的位置相对更加靠前，在网络中也相对更为重要。

本文在SSAM 方法部分参考杨剑楠等［6］研究工作中的实验设置。在LSTM 方法模块通过调节LSTM 中的隐藏层数目（L）、大小（H）以及训练迭代轮数（M）寻找最佳的模型设置。在线性加权部分通过不同线性模型对比预测效果。本文首先固定LSTM 中的超参数L、H、M分别为8、1、10，采用线性回归模型作加权处理，交叉验证中的K值取5。表2为不同训练策略的实验结果比较。

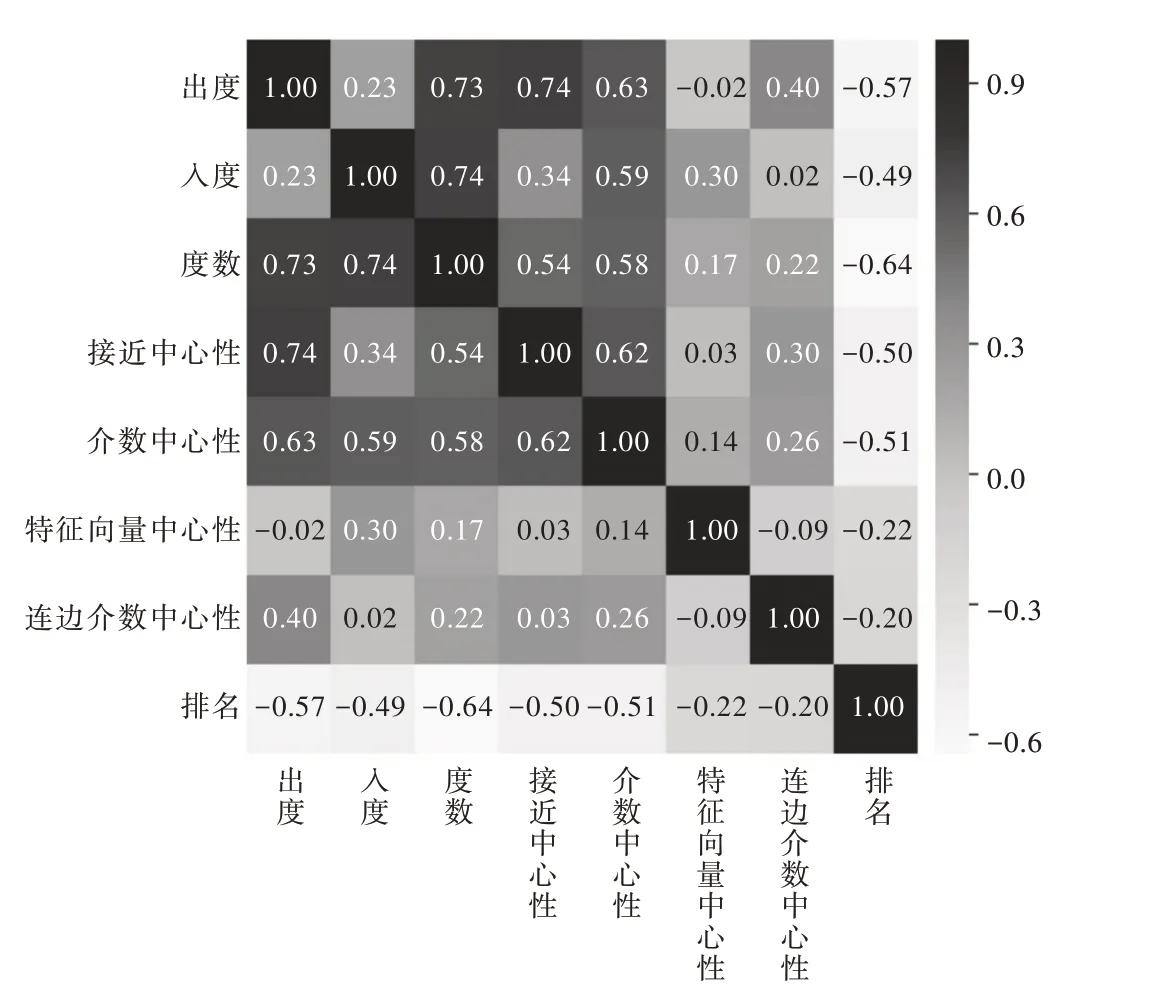
Fig.2 Correlation comparison of each feature and node ranking图2 各特征及节点排名相关性比较

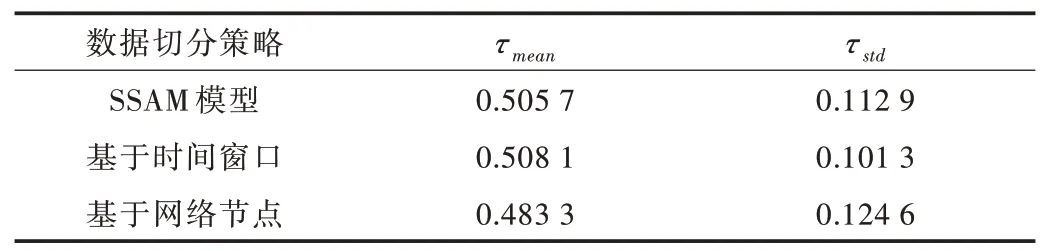
Table 2 Comparison of experimental results of different training strategies表2 不同训练策略实验结果比较

其中，τmean、τstd分别表示10 个时间网络层上对应方法得到的节点重要性排序，以及采用节点删除法得到节点排序的Kendall's τ均值和标准差。根据实验结果对比，基于时间窗口的切分方法训练结果优于单独使用SSAM 方法以及基于网络节点的切分方法。基于节点的切分方法没有取得较好效果的原因在于，在本文使用的Workspace 数据集中，当20%的节点被用于验证模型时，一部分重要节点在训练中可能没有被充分利用，导致LSTM 方法未能学习到足够有价值的信息。

本文通过实验不同的超参数组合寻找模型的最佳性能。本文主要调节的超参数有隐藏层数目、隐藏层大小、迭代轮数及回归模型等，其中优化器采用Adam 优化算法，最大迭代轮数均为10 轮，实验结果如表3 所示。其中，LR表示线性回归模型（Linear Regression），RT 与XGB 分别表示回归树（Regression Tree）和梯度提升树（XGBoost）。

实验结果表明，当隐藏层数为1，大小为8，线性模型选择XGB 时，模型的预测准确率最高，每个时间层网络上的准确率相对较为稳定。固定加权模型为XBG，在不同的参数设置下，每个时间层网络上的Kendall's τ值如图3 所示；固定模型参数设置，选取不同加权模型时各时间层网络上的Kendall's τ值如图4 所示。

Table 3 Experimental results of different parameter settings表3 不同参数设置实验结果

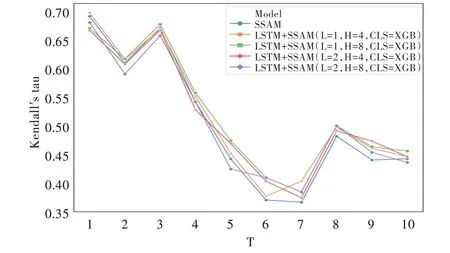
Fig.3 Comparison of model parameter settings and experimental results图3 模型参数设置实验结果比较

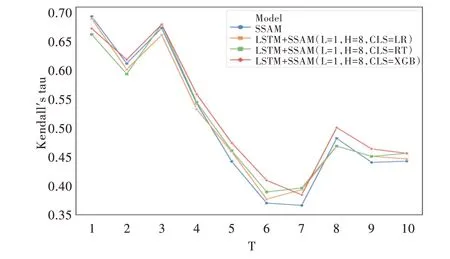
Fig.4 Comparison of experimental results of different weighting models图4 不同加权模型选取实验结果比较

以上结果表明，本文提出融合LSTM 方法的混合模型使时序网络各时间层上关键节点的识别准确率平均值比单一的层间相似度方法提高了1.44%，能更准确地在时序网络中预测出节点的重要性排序。此外，融合了LSTM 方法的混合模型虽然在时序数据前期（t≤4），由于没有得到足够的前序数据用于拟合模型，其识别准确率略低于单一SSAM 方法的结果，但在时序网络中后期（t≥5），混合模型得到的结果更优。LSTM 模型的加入在一定程度上可以解决SSAM 方法在时序网络中后期准确率降幅过大的问题。

4 结语

本文基于Workspace 数据集，通过融合深度学习方法与基于层间相似度的SSAM 方法，构建混合模型挖掘时序网络中的关键节点，获取节点的重要性排序。实验结果表明，融合深度学习模型的方法预测出的节点重要性排序不仅准确率均值与标准差优于单一的SSAM 方法，而且能够有效提升SSAM 方法在时间层网络中靠后序列上的识别准确率。本文通过实验证明融合深度模型能够在一定程度上弥补传统基于层间相似度方法的缺陷，并辅助其提高预测准确率，该实验结果对时序网络中重要节点的挖掘与识别研究工作具有积极意义。同时，本文研究还存在一些不足，如特征选取和数据预处理可能会对结果造成一定影响，另外模型的选取、优化及训练方式的调整都是可以继续深入探索的方向。未来工作可以考虑融合更复杂的模型，选取更多数据和特征进行挖掘与分析。