钢箱梁喷砂除锈并联机器人喷枪轨迹智能优化
2021-08-24高仕琳高国琴方志明
高仕琳,高国琴,方志明
(江苏大学电气信息工程学院,江苏镇江 212013)
0 引言
喷砂除锈是钢箱梁防腐处理中最基础、最重要的环节,除锈质量直接影响后续喷涂的涂层质量与防腐效果[1-2]。表面粗糙度作为检验喷砂除锈的重要技术指标,直接影响着涂层附着力,关乎钢桥的防腐能力。因此,钢箱梁喷砂除锈并联机器人进行喷枪轨迹优化时,需保证表面粗糙度符合工艺要求。
钢箱梁喷砂除锈环境漫天粉尘,难以通过机器视觉等技术实时监测表面粗糙度,目前仅能在人工喷砂后借助表面粗糙度样板或表面轮廓仪测定。因此,钢箱梁自动喷砂除锈并联机器人需首先解决钢箱梁表面粗糙度难以实时检测的问题。喷砂作业表面粗糙度主要受磨料、气压、喷射角度、喷射距离等参数影响。目前,已有国内外学者针对上述参数对表面粗糙度的影响趋势进行了研究,并根据研究结果优化相关参数以保证表面粗糙度符合工艺要求[3-6]。然而,现有研究尚未对表面粗糙度与相关参数之间的关系进行定量分析,因此仅能根据大量喷砂实验数据确定各参数取值,如此以来不仅工作量大,还很可能产生随机误差,不能解决钢箱梁表面粗糙度的实时检测问题。
针对难以实时检测诸如喷砂、喷丸、微磨料气射流等空气磨料射流工艺作业表面粗糙度的问题,已有学者将预测模型的概念应用于上述工艺表面粗糙度的定量研究,基于模型计算表面粗糙度,优化相关参数,以获得最佳喷砂效果。文献[7]研究了硼硅酸盐玻璃微磨料气射流加工时磨料大小、喷射速度与喷射角度对表面粗糙度的影响,并根据实验数据建立了表面粗糙度模型;文献[8]基于6061铝合金工件喷丸有限元仿真模型进行喷丸试验,建立了一个反映初始表面粗糙度、喷丸粒径、喷丸速度与表面粗糙度之间关系的预测模型,并验证了该模型的有效性;文献[9]针对影响气动喷丸表面粗糙度的喷丸粒径、气压、喷丸时间3 个参数,建立了表面粗糙度预测模型,并采用响应面法优化该模型各项参数。虽然喷砂、微磨料气射流与气动喷丸同属空气磨料射流,且原理、设备相似,但其选用的磨料不同,主要用途也有所区别。此外,钢箱梁喷砂除锈并联机器人喷砂作业的表面粗糙度仅受喷射距离、喷射角度与喷枪移动速度的影响,因此现有表面粗糙度预测模型应用于并联机器人难以获得理想的喷砂效果。
目前,复杂曲面喷枪轨迹通常基于曲面分片造型进行分层规划[10],其中各片面喷枪轨迹的连接问题已成为研究热点。针对复杂曲面分层规划后的喷枪轨迹组合优化问题,文献[11-12]利用哈密尔顿图将其转化为广义旅行商问题,分别采用遗传算法、蚁群算法对其求解,但并未涉及大曲率曲面喷枪轨迹的组合优化。针对大曲率曲面喷枪轨迹的组合优化问题,文献[13]采用智能粒子群算法对直纹曲面分片的喷枪轨迹进行了组合优化;文献[14-15]基于智能粒子群算法,提出一种新的组合优化算法,实现了喷枪轨迹的全局优化。然而,上述喷枪轨迹组合优化研究均是针对特定大曲率曲面展开,并不能很好地适用于钢箱梁的复杂曲面。
喷砂除锈效率即单位时间内喷砂除锈的有效面积,当设备、磨料及压强等因素确定时,该指标仅由喷射距离、喷射角度与喷枪移动速度决定[16]。因此,为在保证表面粗糙度符合工艺要求的同时提高喷砂除锈效率,本文采用多元拟合建立钢箱梁喷砂除锈作业表面粗糙度预测模型,该模型可反映喷射距离、喷射角度、喷枪移动速度与表面粗糙度之间的定量关系。基于该预测模型,提出一种既考虑喷砂质量又兼顾喷砂除锈效率的喷枪轨迹智能优化方法。该方法不仅有效解决了钢箱梁表面粗糙度难以实时检测的问题,而且通过喷枪轨迹智能优化提高了喷砂除锈效率。
1 表面粗糙度预测模型建立
1.1 喷砂除锈试验设计
在诸多影响表面粗糙度的参数中,选取影响最为显著且可控的3 个喷枪轨迹参数:喷射距离、喷射角度、喷枪移动速度,对其与表面粗糙度之间的关系进行研究。根据实际喷砂除锈作业条件,选择各参数水平,并对各因素的取值进行优化配置,具体如表1 所示。其中A 为喷射距离(单位:mm),B 为喷射角度(单位:°),C 为喷枪移动速度(单位:m/min)。
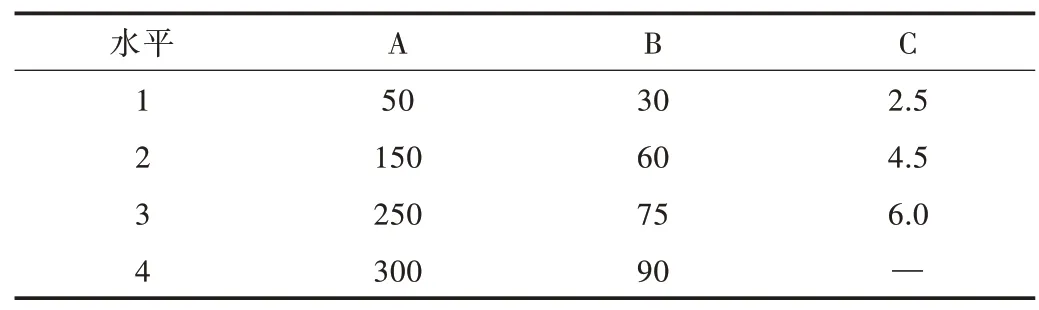
Table 1 Test factor level表1 试验因素水平
根据实际喷砂除锈作业要求,选用粒度为G14~18、硬度为HRC40~50、直径为1.0~1.7mm 的棱角钢砂对钢箱梁所用钢材进行喷砂除锈全因子试验,最后采用表面轮廓仪测量喷砂后钢材的表面粗糙度值。
1.2 单因素分析
喷射距离、喷射角度与喷枪移动速度对表面粗糙度的影响分别如图1、图2、图3 所示。由图1 可知,表面粗糙度随着喷射距离的增加先减小后增大。这是由于随着喷射距离的增加,钢砂射流束不断发散,钢砂在钢板表面的叠加效果也随之减少,表面粗糙度值减小,但当喷射距离增加到一定值后,由于此时作用到钢板单位面积上的磨料过少,后续钢砂无法去除之前钢砂作用产生的凹痕边缘,故而表面粗糙度值有所增大。
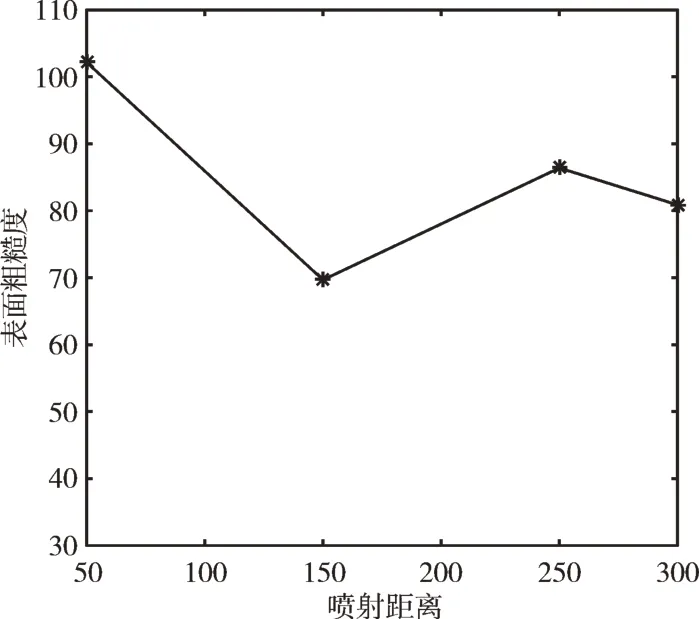
Fig.1 Effect of spray distance on surface roughness图1 喷射距离对表面粗糙度的影响
如图2 所示,表面粗糙度随着喷射角度的增加先增大后减小,且在60°~90°之间变化幅度较小。随着喷射角度的增大,钢砂作用于钢板表面垂直方向的冲击力增大而水平方向的切削力减小,钢砂在其表面留下的凹痕也随之加深。但当喷射角度大于75°时,由于后续钢砂作用于单粒钢砂产生的凹痕边缘使得凹痕变浅,表面粗糙度值也会略有减小。

Fig.2 Effect of spray angle on surface roughness图2 喷射角度对表面粗糙度的影响
如图3 所示,表面粗糙度随着喷枪移动速度的增大先减小后增大,这是由于随着喷枪移动速度的增加,钢砂在钢板表面的有效叠加作用不断减弱,留下的凹痕深度也随之减小。当喷枪移动速度减小到钢砂在钢板上无叠加作用后,钢板上单粒钢砂作用的凹痕边缘不会被后续钢砂削除,此时凹痕深度会稍稍增大,表面粗糙度值也将相应增大。
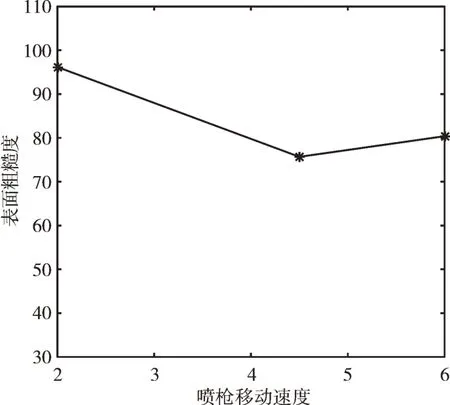
Fig.3 Effect of spray gun moving speed on surface roughness图3 喷枪移动速度对表面粗糙度的影响
1.3 多元拟合建模
漫天粉尘的恶劣喷砂环境难以借助机器视觉等技术在喷砂除锈作业时对钢板表面粗糙度进行实时监测。为解决上述问题,结合已获得的实验数据,采用多元拟合建立适用于并联机器人喷砂除锈作业的表面粗糙度预测模型,定量评价上述参数对表面粗糙度的影响,并根据它们之间的定量关系优化相关参数,以保证喷砂除锈后表面粗糙度符合工艺要求。通过多元拟合分析得到的表面粗糙度预测模型为:
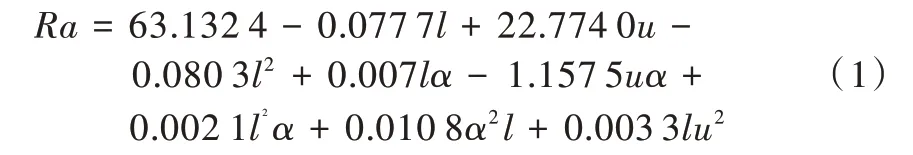
在获得表面粗糙度预测模型后,需要检验其显著性,并由此判断其拟合效果。为此,本文通过F检验法检验该模型的显著性,检验得到p=0.002 4,远小于0.05,说明回归模型高度显著。
2 喷枪轨迹参数优化
2.1 喷砂除锈效率
喷砂除锈作业时,喷枪作用于钢箱梁的喷射示意图如图4 所示。钢砂束喷射到钢板上的有效范围可近似看为椭圆[16],其长轴、短轴与喷射距离、喷射角度及喷枪移动速度3 个参数之间的关系可近似表示为:
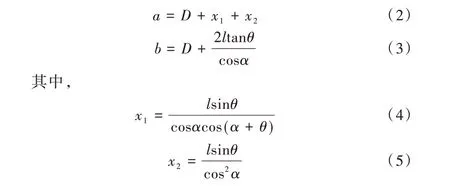
式中,a为椭圆长轴长度(单位:mm),b为椭圆短轴长度(单位:mm),D为喷嘴内直径(单位:mm),θ为钢砂射流束的有效散射角度(单位:°)。

Fig.4 Schematic diagram of sand blasting and rust removal图4 喷砂除锈示意图
为满足轨迹转折点最少的喷枪轨迹规划原则,喷砂除锈时喷枪应沿着椭圆短轴方向移动,即图5 所示的喷枪轨迹行程间距d为椭圆长轴长度。表示为:
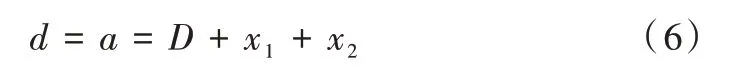
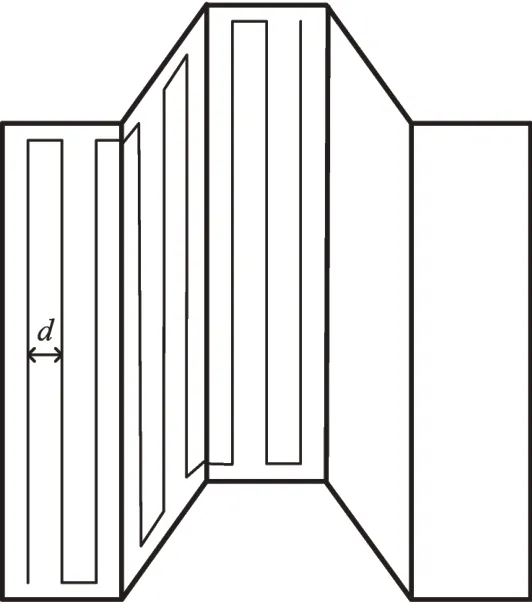
Fig.5 Schematic diagram of spray gun trajectory图5 喷枪轨迹示意图
喷砂除锈效率即单位时间内喷砂除锈作业的有效清理面积,可表示为:

式中,f为喷砂除锈效率(单位:mm2/min),Δt为单位时间(单位:min),S为单次喷砂除锈的有效清理面积(单位:mm2),可表示为:

2.2 喷枪轨迹参数优化模型
为在保证喷砂除锈后钢箱梁表面粗糙度符合工艺要求的前提下提高喷砂除锈效率,基于已建立的表面粗糙度预测模型,设定能保证表面粗糙度符合工艺要求的约束条件,建立以喷砂除锈效率为优化目标的喷枪轨迹参数优化模型。表示为:
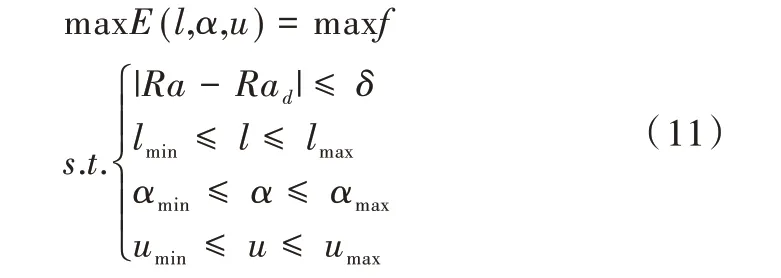
式中,Rad为表面粗糙度的期望值(单位:μm),δ为表面粗糙度所允许的误差范围(单位:μm),lmin为最小有效喷射距离(单位:mm),lmax为最大有效喷射距离(单位:mm),αmin为最小有效喷射角度(单位:°),αmax为最大有效喷射角度(单位:°),umin为喷枪移动的最小速度(单位:mm)umax为喷枪移动的最大速度(单位:mm)
根据式(11)所示的轨迹参数优化模型,求解最佳喷射距离ld、喷射角度α d与喷枪移动速度ud,从而得到各片面最佳喷砂除锈效率的喷枪轨迹。
3 各片面间喷枪轨迹组合优化
为简化复杂曲面各片面轨迹的组合优化问题,将其转化为一个广义旅行商问题[11-15]。将曲面造型后各片面上的轨迹看作是一条边,各片面喷枪轨迹组合优化可表示为哈密顿图G(V,E,C,ω:E→Z+),其 中V为顶点集,E为边集,C为E中的任意子集,ω为各边权值,即各片面喷枪路径长度,在图G中找出只经过各边一次且距离最短的喷枪轨迹组合连接方案。
目前蚁群算法[11]、遗传算法[12]两种智能仿生算法已成功应用于广义旅行商问题的求解。然而,钢箱梁附有U 型肋等不规则件,表面结构复杂,增加了求解该问题的复杂度,使得遗传算法的冗余迭代增加,求解效率降低,甚至陷入局部最优;蚁群算法也会因前期信息素匮乏而陷入局部最优。
从求解速率来看,大量研究表明在搜索前期遗传算法的求解速率更快,更适用于大范围搜索[17-20],如图6 所示。为此,本文在蚁群算法的基础上融入遗传算法对各片面间喷枪轨迹进行组合优化。在算法前期运用遗传算法产生的最优解初始化蚁群算法的信息素[21-22],缩小最优解的搜索范围;后期采用蚁群算法继续搜索,从而有效避免陷入局部最优,提高搜索效率,最终获得表面粗糙度符合工艺要求且喷砂除锈效率最佳的喷枪轨迹。具体流程如图7所示。
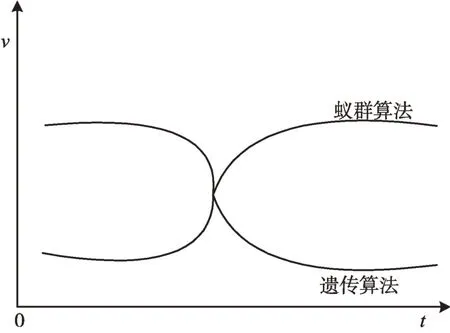
Fig.6 Comparison of solving rate between ant colony algorithm and genetic algorithm图6 蚁群算法与遗传算法求解速率对比
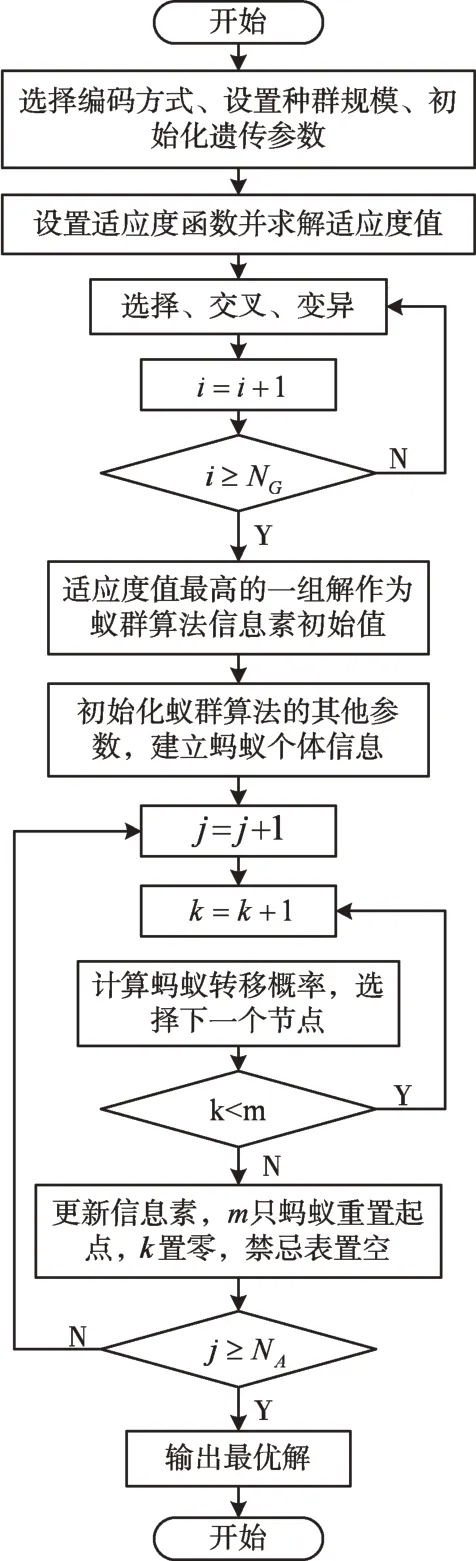
Fig.7 Flow of genetic ant colony algorithm图7 遗传蚁群算法流程
4 仿真实例
为体现钢箱梁复杂曲面的特征,选取如图8 所示的钢箱梁局部模型作为仿真对象,根据最佳喷枪轨迹参数,采用文献[17]中的边界盒子法生成该模型分片造型后各片面的喷枪轨迹,基于本文设计的遗传蚁群算法求解该喷枪轨迹的组合优化问题。

Fig.8 Local model of complex curved surface of steel box girder图8 钢箱梁复杂曲面局部模型
搜索前期的遗传算法设置交叉概率pc=0.8、变异概率pm=0.07、最大迭代次数NG=20,并将迭代后适应度值较高的解用以初始化蚁群算法的信息素,缩小搜索范围;搜索后期的蚁群算法参数设置如下:蚂蚁数m=10、最大迭代次数NA=100、信息素重要程度因子α=1、启发函数重要程度因子β=0.8、常系数Q=1.5、信息素挥发率ρ=0.08。坐标选择如下:

实验优化结果如图9 所示,迭代计算过程如图10 所示。结果表明,运算28 次即可得到最优喷涂轨迹长度为12 940mm,证明该轨迹优化算法收敛。此时喷砂除锈效率高达115.435 2m2h,约为人工喷砂除锈效率的11.5 倍,已达到高效喷砂除锈要求,进一步证明了该轨迹优化方法的有效性。
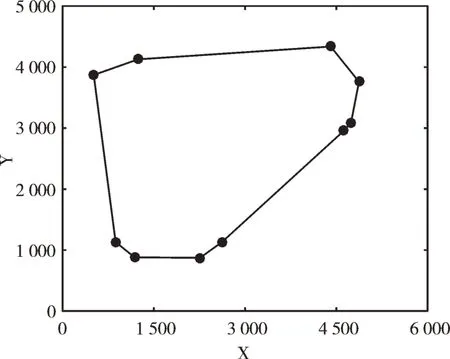
Fig.9 Optimization results图9 优化结果

Fig.10 Iterative calculation process图10 迭代计算过程
5 结语
针对钢箱梁喷砂除锈并联机器人喷砂除锈作业,提出一种既考虑喷砂质量又兼顾喷砂除锈效率的喷枪轨迹智能优化方法,并通过仿真实验验证了该方法的有效性。仿真结果表明,该方法在保证表面粗糙度符合工艺要求的同时提高了喷砂除锈效率,高达人工喷砂除锈效率的11.5倍,满足了高效喷砂除锈的要求。
目前,喷砂除锈机器人多为双喷嘴,而本文研究的钢箱梁喷砂除锈并联机器人为单喷嘴。后续可在此基础上对双喷嘴喷枪轨迹优化展开研究,以提高该方法的通用性与实用性。
