随机弹射结合DNA 编码的图像加密算法

司宇晨，滕 琳，孟 娟

（1.大连海洋大学信息工程学院；2.设施部重点实验室；3.辽宁省海洋信息技术重点实验室；4.大连海事大学信息科学技术学院，辽宁 大连 116023）

0 引言

随着大数据时代的到来，越来越多的人开始重视信息数据安全，而图像作为当前信息传输的主要途径其重要性不言而喻［1］。图像传输安全是一项非常重要且必要的任务，由于数字信息的特征，其在传播时极易遭到他人的截取和篡改，传统的加密算法已不能满足当前图像加密需求。混沌系统有着良好的初值敏感性、随机性和不确定性，在图像加密领域有着良好应用前景。因此，许多基于混沌系统的图像加密算法应运而生［2-5］。

DNA 编码是由计算机技术和生物学结合而产生的一个新学科，由于DNA 的特性，DNA 编码可以拥有8 种编码方式和3 种运算规则，因其强大的并行计算能力和高复杂度在信息加密中有着独特优势［6］。Zhang 等［7］提出一种基于DNA 编码双重混沌映射的图像加密算法，但加密算法不可逆；Ping 等［8］提出一种运用Henon 混沌映射的图像像素位置置乱算法，但是没有考虑像素值扩散，系统复杂度低；Wu 等［9］提出一种典型加密算法，但其密钥与明文无关，易于明文攻击攻破。

针对上述图像加密算法的不足，本文提出一种基于混沌系统控制随机弹射矩阵与DNA 编码相结合的图像加密算法。首先运用哈希算法获取混沌系统初始值，其次对明文图像进行分层处理及Arnold 置乱，然后利用对置乱后的图像进行分块以及DNA 编码，最后与随机弹射矩阵进行DNA 运算，将三层分量合并后生成密文图像。通过仿真测试表明，该算法拥有大密钥空间及高抗攻击性，安全性能更强。

1 基本理论

1.1 Logistics 混沌系统

一维Logistics 混沌映射也称作虫口模型，它也是众多混沌系统中较为常用的一种。20 世纪50 年代，许多科学家利用此方程推断种群变化特征，因为此系统在动力学方面有十分复杂的特征，因此在信息保密方面有较多应用。Lo⁃gistic 的数学表达式如式（1）所示。

其中a为参数，{xn}为生成的混沌序列，当x∈(0,1)，a∈(3.569 945 6,4]时，Logistics 系统呈混沌状态。

1.2 MD5 算法

MD5 算法是一种被广泛用于加密的散列函数，对明文像素改变一位像素值，散列值就会发生很大改变，且运算结果不可逆。MD5 算法也可以理解成信息摘要的一种实现，它可以从任意长度的明文字符串生成128 位的哈希值；即运用明文图像和MD5 算法生成128 位（16 字节）的散列值U。本文将128位的散列值U分成16 个子块（k1,k2,k3,…k16），如式（2）所示，将其处理后，可作为混沌系统的初始值，其作为密钥与明文图像相关联，也极大加强了安全系数。

1.3 随机弹射矩阵

本文提出随机弹射矩阵，首先选取与明文图像相同大小零矩阵，运用明文图像结合MD5 算法设定Logistics 系统初值x，如式（1），定义其公式如式（3）所示，其中⊕代表异或运算。参数a=3.678 9，获取Logistic 混映射连续迭代生成的伪随机序列然后去除前3 000 次，使其达到充分迭代，选取长度为M的序列将生成序列经过式（4）转化为0～π的弧度值。

选取点（1，1）为初始位置进行弹射，碰壁后取与矩阵边的夹角进行折射，若弹射至4 个顶点，则返回初始位置，继续进行。统计出路径经过每个单元格的次数，用来生成随机矩阵R。图1 为随机弹射示意图，其中A 为初始点。

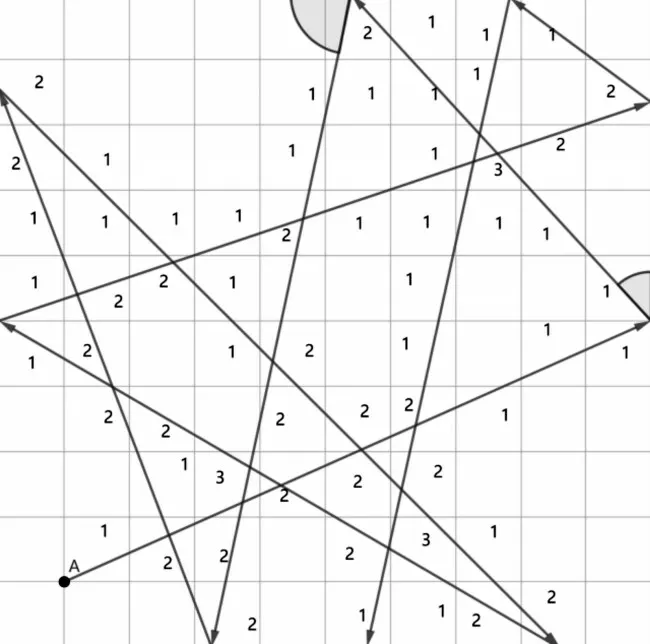
Fig.1 Random ejection diagram图1 随机弹射示意图

1.4 Arnold 置乱

Arnold 也称为猫映射，由俄国数学家Vladimir Igorev⁃ich Arnold 提出［10］。Arnold 变换是一种在固定区域内反复迭代拉伸、折叠的映射，其原理主要是沿图像x轴方向错切变换，再做y轴方向的错切变换，最后进行回填。一副M*N的数字图像的二维Arnold 变换定义为：

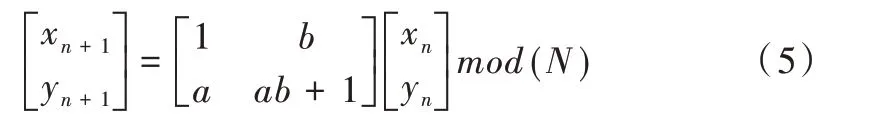
其中，x、y表示变换前图中像素位置，xn+1、yn+1表示变换后的像素位置，a、b为参数，n表示当前变换次数，N为图像的长或宽。

1.5 Chen 超混沌系统

陈氏混沌系统（Chen Chaotic System）是在20 世纪末被提出的一种新的混沌系统，动力学方程如式（6）所示。

其中，a、b、c、d、r分别为超混沌系统的参数，当a=35,b=3,c=12,d=7,r∈[0.085,0.798]时，Chen 超混沌系统呈混沌状态。将a=35,b=3,c=12,d=7,r=0.6 代入Chen超混沌系统式（2），用龙格库塔法［11］求出4 个混沌序列，图2（a-d）为混沌系统4 个引子相图。

Fig.2 Attractor phase diagram of Chen hyperchaotic system图2 Chen 超混沌系统吸引子相图

1.6 DNA 序列

在生物学中，DNA 的全称是脱氧核糖核酸，因其存在4种碱基：A、T、C、G 分别是腺嘌呤、胸腺嘧啶、鸟嘌呤、胞嘧啶，它们之间有互补配对原则，因而也常常被用在二进制的互补关系中。如果用两位二进制表示碱基之间的编码方式，共可分为24 种编码方式，但是满足碱基互补配对原则的只有8 种编码方式如表1 所示。

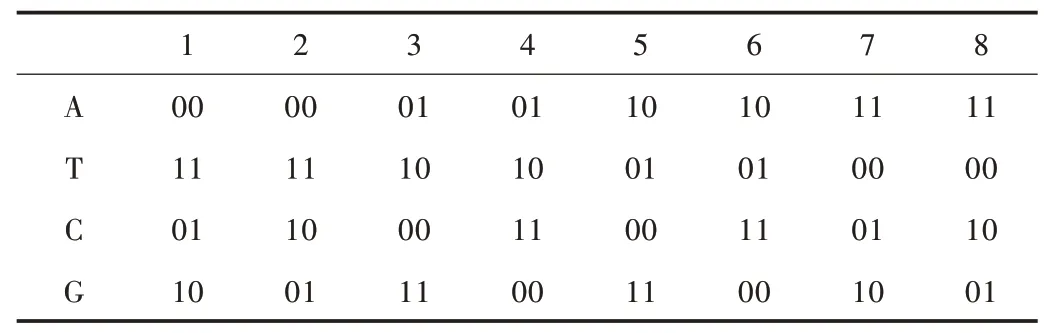
Table 1 DNA coding rule表1 DNA 编码规则

系统运用到的DNA 运算规则有3 种，分别是DNA 加法运算、DNA 减法运算和DNA 异或运算。运算规则如表2—表4 所示。

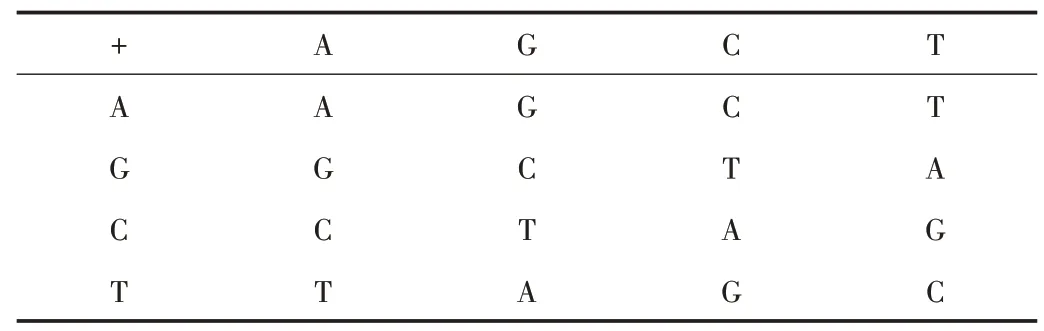
Table 2 DNA addition rules表2 DNA 加法规则

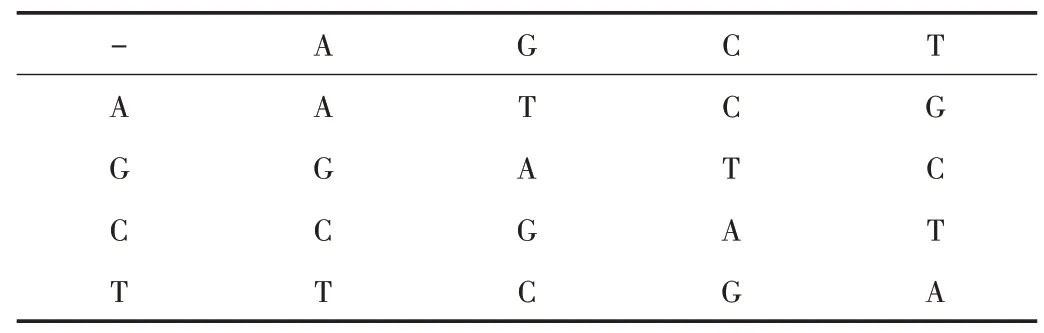
Table 3 DNA subtraction rules表3 DNA 减法规则

Table 4 DNA XOR rule表4 DNA 异或规则

以上3 种运算规则是基于第一种编码规则而呈现，当然不同的编码规则所得到的运算结果不同。

2 加密算法

本文提出的图像加密算法主要是将图像分为3 个二维矩阵，对每个二维矩阵经过置乱、分块、DNA 编码处理后与随机弹射矩阵进行DNA 运算。Logistics 混沌系统决定随机弹射矩阵的生成，Chen 超混沌系统决定每一个子块的编码解码及DNA 运算方式。两个混沌系统的初值都与原始图像关联，很大程度地提升了算法安全性。具体加密流程如下：

（1）输入M×N的彩色明文图像P，进行R、G、B 分层，并按式（7）转化为3 个二维矩阵。

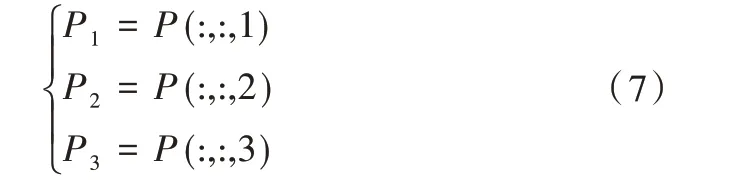
（2）取U生成k1、k3、k5、k7的值，设定Logistics 系统（式（1））初值x1如式（8）所示，获取Logistic 混映射连续迭代生成的伪随机序列｛Jx｝如式（9）所示，去除前3 000 次，使其达到充分迭代，对分层后的图像进行Arnold 置乱，规定P1置乱迭代次数为｛J1｝，P2置乱迭代次数为｛J100｝，P3置乱迭代次数为｛J1000｝，其中N为图像的边长。

（3）将置乱后的P1P2P33 个分量的二维矩阵进行分块，为使P1P2P3都能够分为均匀的块，因此对其进行补零操作，t为分块数，具体补零方法如式（10）所示。

（4）对Chen 氏混沌系统设定初值，运用龙格库塔法［11］算出Chen 氏超混沌系统的解，得到4个序列。其中，初值设定方法由式（11）计算得出。取U生成k1、k2、k3、k4的值做异或运算作为{Xi}的初 值。依次类推，{Yi}的初值由U的k5、k6、k7、k8子块决定，{Zi}的初值由U的k9、k10、k11、k12子块决定，{Wi}的值由U的k13、k14、k15、k16子块决定。

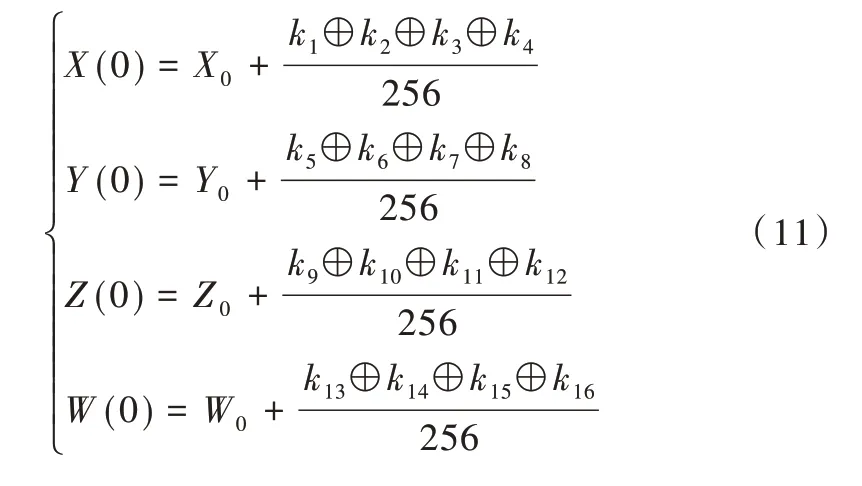
（5）取{Xi}和{Yi}分别控制P1、P2、P3和随机弹射矩阵R 的编码方式，将{Xi}、{Yi}分别由式（12）转化为1～8 之间的整数，用来决定DNA 的8 种编码方式，P1、P2、P3中，第i个子块的编码方式为Xi，随机矩阵R 中，第i个子块的编码方式为Yi。按照{Zi}控制编码后的P1、P2、P3与随机弹射矩阵R 的运算方式，同理将{Zi}中所有序列值按式（12）转化为0～2 之间的整数，当Zi=0 时，DNA 运算方式为加法；Zi=1 时，运算方式为减法；Zi=2 时，运算方式为异或。

（6）为提高算法加密效果，将运算后每个子块与前一个子块再进行一次DNA 运算，达到充分扩散效果后，对经过运算的矩阵按式（13）中{Wi}的值进行解码，因为解码是编码的逆运算，因此解码方式也有8 种。

（7）将解码后的三层分量合并，形成密文图像。

本文提出的加密算法解密过程是加密算法的逆运算，在密钥正确的情况下，即可恢复出明文图像，但在DNA 运算时要注意减法和加法置换。加密算法流程如图3 所示。

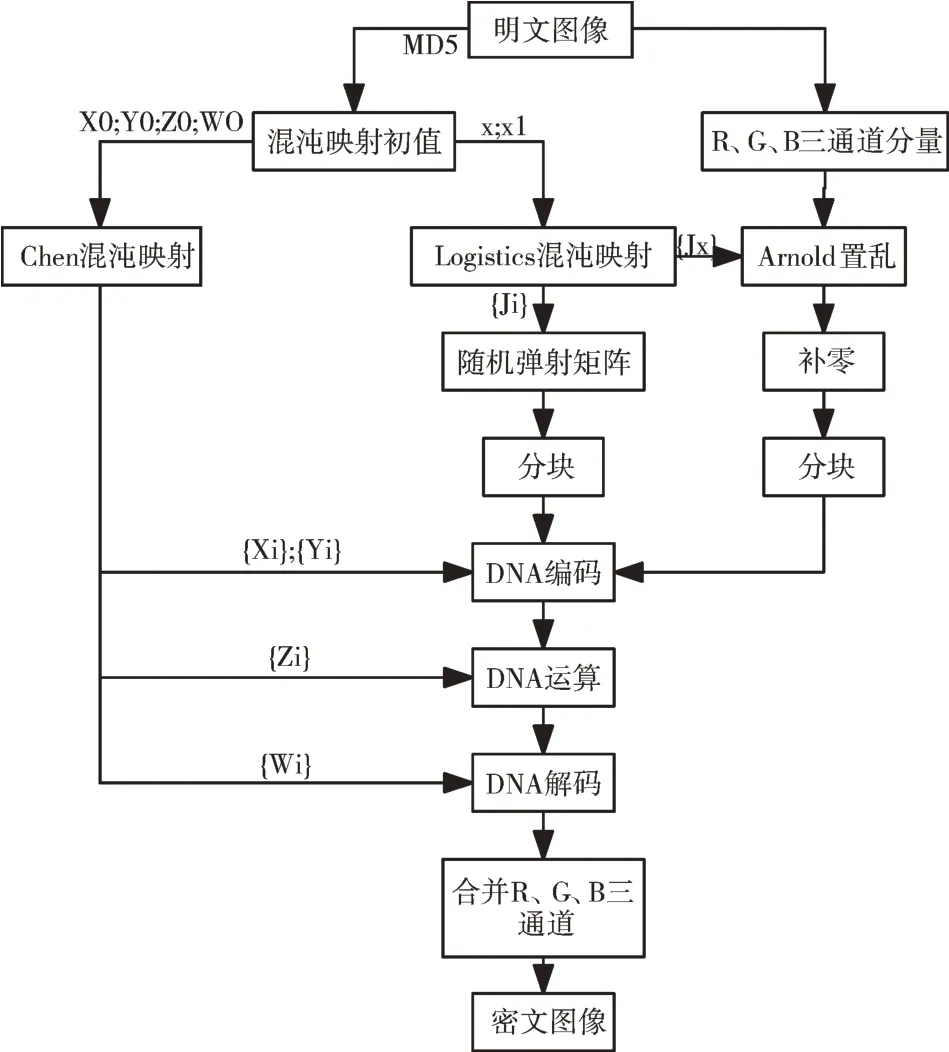
Fig.3 Brief flow of image encryption图3 图像加密简要流程

3 实验结果与分析

该算法是在Intel Core（TM）i5-9300H CPU@ 2.40GHz、8G RAM、win10 64 位操作系统、Matlab R2018a 下实验环境下完成。选取512×512 的Lena、Baboon、Airplane 图作为测试图像。其中，随机弹射矩阵和分量置乱的Logistics 映射初始值由MD5 算法获取，μ 取3.79。对Chen 超混沌系统取a=35,b=3,c=12,d=7,r=0.6。加密效果如图4（a-i）所示。

Fig.4 Contrast image encryption before and after图4 图像加密前后对比

通过图像加密前后对比图可以看出，密文图像与明文图像毫无关联，掩盖了明文信息，而解密效果展现了明文的全部信息，说明该加密算法可行且效果良好。

3.1 直方图分析

直方图可以有效地分析图像中每个像素值出现的频率，因此像素值分布越均匀，说明该图像所有像素值出现的频率越均衡，可利用信息越少。图5 是以Lena 图为例R、G、B 3 个通道加密前后直方图的对比图。

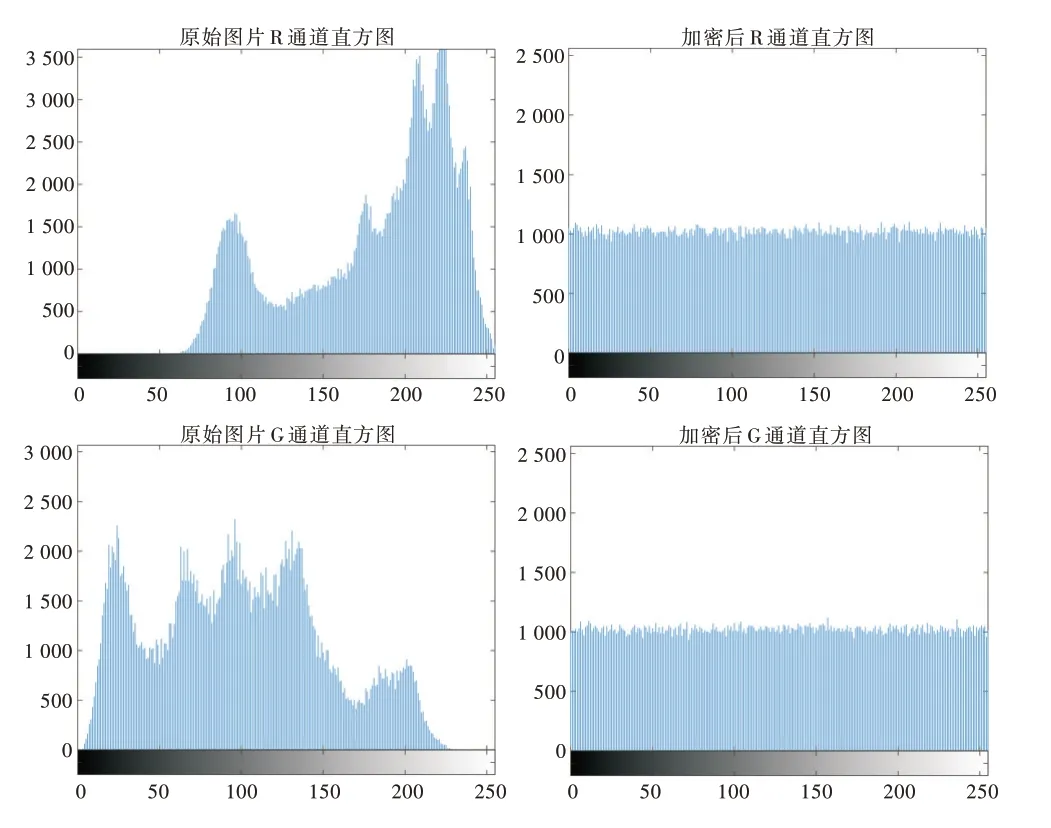
Fig.5 Histogram comparison before and after encryption图5 加密前后直方图对比

可以得知，加密前3 个通道的直方图，分布不均且波动性强，而加密后3 个通道的直方图分布均衡，具有近乎相同的分布趋势，因此本加密算法也可以很好地抵抗针对图像统计分析方法的攻击。

3.2 相邻像素相关性分析

自然图片的相邻像素具有很强的相关性。以Lena 图为例，选取加密后的Lena 图的水平、垂直、对角线3 个方向，随机选择1 000 相邻像素进行相关性测试，式（12）—式（13）结果如表5 所示，计算公式如式（14）所示。

Table 5 Correlation of horizontal，vertical and diagonal adjacent pixels表5 水平、垂直、对角线相邻像素相关性

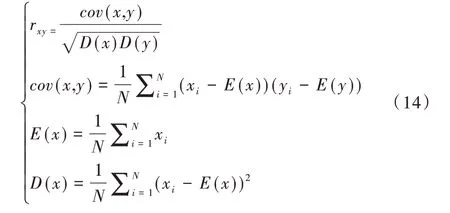
其中，x、y表示明文图像与密文图像相邻像素值，N表示选择参与的像素点总数，E（x）、D（x）、cov（x、y）分别表示计算公式的期望、方差、协方差，rxy表示相邻像素点的相关系数。

可以看出，明文图像的相邻像素相关系数十分接近1，这说明相邻像素相关性很强，而本文提出的加密算法加密后各通道的相邻像素相关系数比另外两种算法系数更接近于0，说明各相邻像素之间的关系几乎被消除。

以Airplane 图为例，图6 是加密前后R 通道的水平、垂直、对角线3 个方向的明文和密文随机点像素灰度值。可以看出，加密图像的相邻像素之间的相关性显著降低，说明该方案具有良好的安全性。

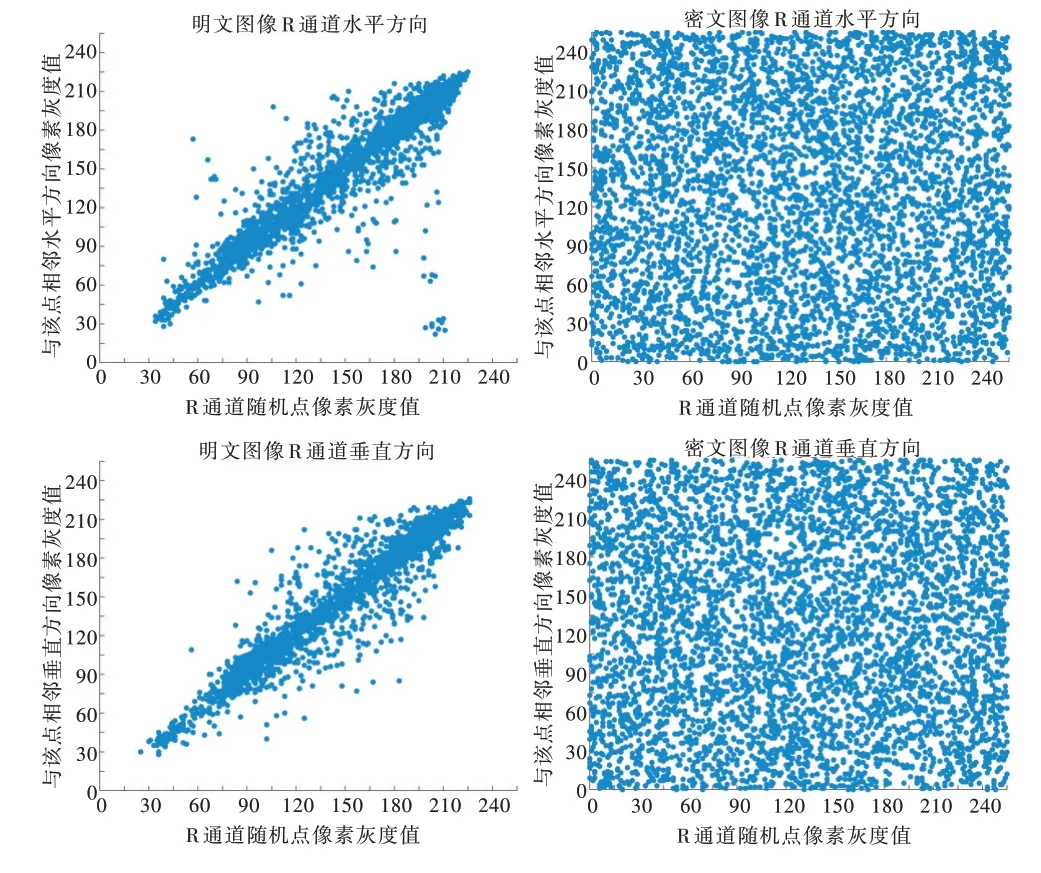
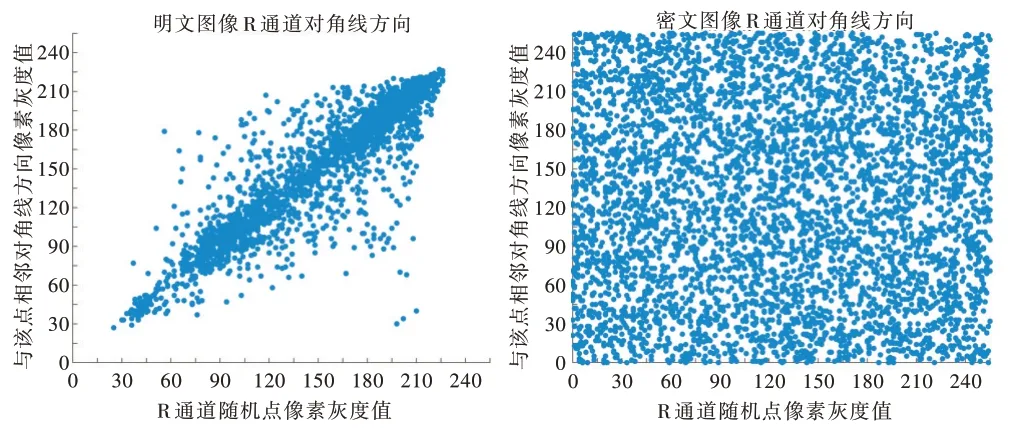
Fig.6 Comparison of pixel values before and after encryption of airplane R channel图6 airplane R 通道加密前后像素值对比

3.3 信息熵

信息熵可以反映出图像的混乱程度，信息熵的值越接近8，意味着图像的随机程度越高，不确定性越大，可利用信息越少。计算公式如式（15）所示。

其中，p（i）表示信号i出现的概率。本文L 值为512，选取Lana 图经测试后，图像各通道的信息熵如表6 所示。

Table 6 Information entropy表6 信息熵

由表6 可得，本文加密算法经加密后的信息熵更接近于8，能够有效抵御统计攻击。

3.4 抗差分攻击

使用本文提出的加密算法对明文图像进行加密，然后改变明文中的一个像素进行重新加密，两次加密图像之间的像素关系可用两个标准衡量，即像素数改变率（Number of Pixels Change Rate，NPCR）和归一化像素平均值（Unified Average Changing Inrensity，UACI）。NPCR 的 理 想 值 是99.609 4%，UACI 的理想值是33.463 5%，在实际数值不同的实验环境下会有上下浮动。计算方式如式（16）—式（17）所示。

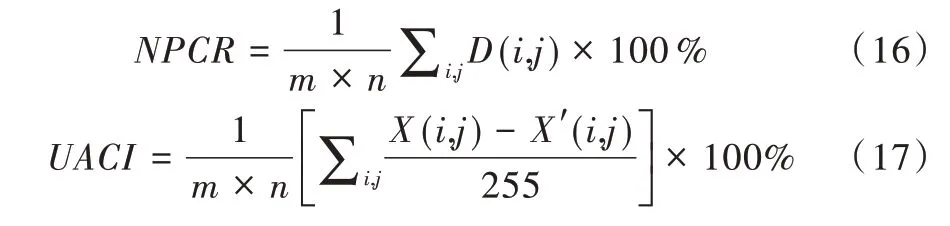
其中，图像宽度由m表示，高度由n表示，表7 是运用本文算法对改变一位像素的两张Lena 图进行加密后的明文敏感性对比。可以看出，本文算法的NPCR 和UACI 接近于理想值，这是因为本文采用的混沌序列初值来源于明文通过MD5 算法提供的散列值并加以运算得到的，即使一位像素发生变化，它也可以有效地改变混沌序列的初值，这种方法极大提升了明文的敏感性，这也说明本文提出的加密算法具有很强的抗差分攻击能力。

Table 7 Contrast of plaintext sensitivity表7 明文敏感性对比

4 结语

本文提出了一种基于混沌控制随机弹射矩阵和DNA序列的图像加密算法，该算法首先利用明文图像和MD5 算法产生混沌映射的初值，然后运用Logistic 映射生成混沌序列转化成控制质点弹射的角度值，统计质点经过每个位置的次数，生成随机弹射矩阵；接着将分层后的明文图像进行Arnold 置乱，对置乱后的图像和随机弹射矩阵进行分块、DNA 编码后作DNA 运算，合并后生成密文图像。在此基础上，通过直方图分析、信息熵值分析、抗差分测试分析等实验，表明本文提出的图像加密算法具有很强的安全性和实用性，具有很好的应用前景。但在加密效率方面还存在一定的提升空间，今后可针对此方面进行合理优化。