结合非对称卷积与复合感受野结构的图像降噪方法

程 龙，蔡光程

（昆明理工大学 理学院，云南 昆明 650500）

0 引言

图像是人们获取信息的主要途径之一。然而，由于外部环境的不稳定性，在获取、压缩与传输过程中，图片难免受到噪声干扰，从而导致质量降低。含噪图像给人们带来糟糕的视觉体验，不利于计算机分析、理解图像，给图像分割、对象识别、基于内容的图像检索、边缘提取等后续图像处理工作带来不便。因此，降噪是图像处理技术中的首要步骤。在空间域上，降噪方法从传统的维纳滤波发展到全变分模型、非局部均值降噪、马尔可夫随机场模型降噪等方法［1-5］；在频率域上，通过小波变换、离散余弦变换、K-L变换（Karhunen-Loeve Transform）压缩或赋零噪声变换域系数可达到降噪目的。研究者们提出了多种算法，在保留图像边缘的同时，取得了较好的降噪效果，其中表现较为突出的是由Dabov 等［6］于2007 年提出的图像块匹配3D 滤波方法（Block-Matching and 3D Filtering，BM3D）。其结合了变换域中小波萎缩法与空间域中非局部均值降噪算法的优点，充分利用图像块之间的自相似性进行图像复原。BM3D 无论在客观评价指标峰值信噪比，还是主观肉眼感受上，均有较为理想的降噪结果。然而，对于高强度噪声，图像中可利用的信息非常少，降噪变得比较困难。

目前，卷积神经网络（Convolution Neural Network，CNN）被应用于图像降噪中。基于CNN 的图像降噪技术避免了现有降噪模型在测试阶段需要复杂优化方法以及手动设置参数的弊端［7］。CNN 由神经网络发展而来，其特有的稀疏连接与权值共享特性使得网络所需参数量剧减，使神经网络方法用于图像处理成为现实。1987 年，Zhou 等［8］开创性地将神经网络应用于图像降噪中，但该方法的巨额参数量使得计算成本较高。1993 年，细胞神经网络使用带模板的节点获得平滑函数，在降噪计算速度上得到提升，但需要人工设置模板参数，且不能灵活添加新的插件单元，限制了其实际应用［9］。2016 年，Zhang 等［10］提出前馈降噪卷积神经网络（Feed-forward Denoising Convolutional Neural Networks，DnCNNs），该网络由VGG16 发展而来，使原本用于图像识别与分类的模型适用于图像降噪工作。该模型吸收了残差学习思想，建立的网络并不直接学习含噪图像到干净图像的端到端映射，而是先得到噪声图像，继而通过跳跃连接，从含噪图像中分离出所需潜在干净图像，同时结合批量规范化操作，在GPU 加速计算下能快速获得较好降噪效果。

以上研究在寻求一种性能优越的降噪算法方面进行了探索。为进一步改善图像降噪技术，本文在非对称卷积与多尺度结构［11-12］的启发下，进行用于图像降噪的卷积网络架构研究。结合二者优势，本文改进了DnCNN 降噪模型，提出一种新型降噪CNN，称为非对称复合感受野卷积网络（Asymmetric Complex Receptive Field Convolution Net⁃work，ACCNet）。

1 ACCNet 降噪模型

采用加入高斯噪声的方法进行测试，相比于其他人工噪声，高斯噪声下进行的仿真更接近于真实噪声。加入高斯噪声的图像v(x,y)可以表示为：

式中，u(x,y)为未被污染的原始图像，n(x,y)为所加高斯噪声。由于受梯度消失、网络退化与复杂度问题影响，架构设计中的一个重要问题是为模型设置合适的深度。网络中大多数卷积核采用文献［10］中使用的3×3 卷积，在非对称复合感受野卷积块（后文用ACCB 表示）中对输入数据做并行处理，各路分别使用64 个64 通道数的3×3、5×5、7×7、9×9 卷积操作，并采用Relu 激活形成对尺度结构。为减少参数量并提升模型精度，正方形卷积核使用3×1、5×1、7×1、9×1 与1×9 的非对称卷积核替代，其中9×1 与1×9 卷积核的串联在感受野上等同于4 层3×3的卷积核，因此ACCB 的感受野大小可由2d+1 计算得到。将网络深度设置为18，得到一个感受野大小为37×37 的网络。原始输入跳跃连接到最后一个卷积层作为残差结构，这种残差映射出的降噪图像比直接映射更容易优化。

深度学习中的CNN 非常适宜于图像降噪，网络层中的卷积核通过数据学习到合适的滤波器参数，激活函数赋予了模型非线性表达能力。与多层感知器相比，CNN 的稀疏连接与权值共享极大减少了模型训练参数量，从而使基于深度学习的图像处理工作在工程上得以实现［13］。本文在较短时间和较低空间复杂度的要求下，架构结合非对称卷积与复合感受野结构的图像降噪网络。模型第1 层为64个尺度为3 的正方形卷积核，用于初步平滑图像和扩展特征图，第2 层为ACCB，第3-14 层每层均为3×3 卷积操作、批量规范化（Batch Normalization，BN）、修正线性单元（Rec⁃tified Linear Unit，ReLU）的交替连接，第15 层将特征图降维到单通道，最后通过跳跃连接从含噪图像中提取干净图像。实验结果表明，本文模型在标准测试图像集Set12 中的降噪性能优于目前许多优秀的降噪方法［5-7，10］。

1.1 ACCB 结构

以往CNN 通常使用尺度为3、5、7 的正方形卷积核，且为了提高模型解容量，卷积层堆叠得越来越多，给计算机带来了极大负担。目前，研究者们正在寻找一种不增加额外卷积层而提高网络性能的方法，例如SENet 通过注意力机制重新标定特征图通道的权值，从而抑制无用特征，增强对结果有积极影响的特征［14］。如图1 所示，本文设计的非对称卷积块同样不需要考虑网络整体结构，直接采用非对称的n×1 或1×n的卷积核替换其中n×n的正方形卷积核，减少了模型需要训练的参数量，并且结合Inception 网络中的多尺度卷积提取特征，将单一输入在不同感受野上进行加权与激活，最终堆叠成为通道数增加的四维张量作为整个结构块输出。这样不仅能提取到图像局部特征，还能提取到较为整体的特征，并且在参数学习过程中决定了不同感受野上特征的使用。

Fig.1 Diagram of ACCB structure图1 ACCB 结构示意图

1.2 深度神经网络中的两个问题

深度网络存在的两个问题值得注意：一是神经元饱和问题，另一个是梯度消失与爆炸问题。

那么，网络逐层前向传播用矩阵的形式可表示为：

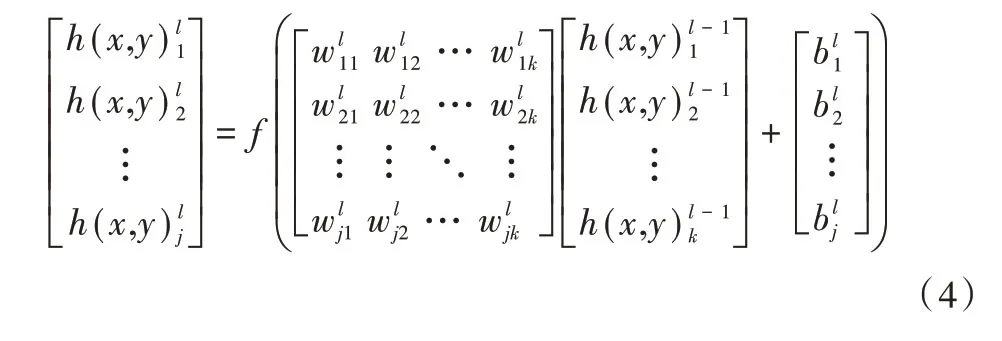
利用式（4）从输入层逐层计算网络激活值。若网络共有n层，损失函数为网络输出与期望输出之间的距离，因此损失函数可表达为网络输出的函数单个数据的损失记为Lh(x,y)nj(w,b)，其中w和b分别为所有需要训练的权值和偏置。n个样本的整体损失可定义为：

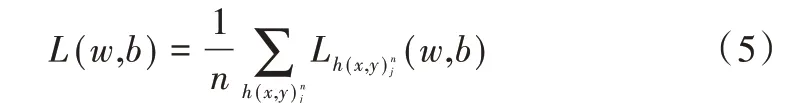
1.2.1 神经元饱和问题

将式（7）扩展为矩阵形式，则有：

则该神经元误差将趋近于零，即有：

激活函数梯度过小，导致神经元无法进行有效的参数更新，神经元在还未找到解决问题的最优参数时便停止了学习，激活函数的饱和导致了神经元饱和问题。

1.2.2 梯度消失与梯度爆炸问题

根据链式法则，得到式（11），通过式（11）、式（12）、式（13）可求得神经元误差反向传播方程式（14）。表示为：

式（15）表明可以通过第l+1 层的神经元误差δl+1计算第l层的误差δl。结合式（6）与式（14），可以计算网络中任意一层神经元的误差。考察损失函数对权值的改变率对偏置可以同样方式说明。假设每个网络层只有一个神经元，根据链式法则有：

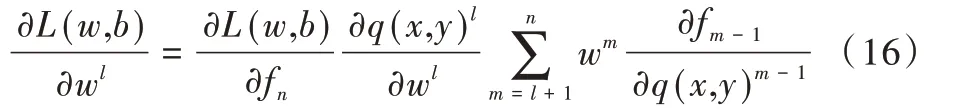
1.3 激活函数选择

在原始感知机中，隐藏层只进行线性操作，这样由卷积层堆叠的深度网络输出相当于输入的线性组合，网络的逼近能力有限，相当于仅采用滤波器处理含噪图像。加入激活函数后，网络的非线性能力提升，深层网络几乎可以逼近任意函数。早期配置的激活函数为Sigmoid 函数、双曲正切函数，其网络学习更新参数的梯度区间过窄，容易使神经元达到饱和，且整体梯度偏小。近年来，受到视觉皮层信号处理的启发，修正线性单元（Rectified Linear Unit，ReLU）被提出并成为最有效的激活函数之一，可表示为式（17）。其在众多激活函数中脱颖而出主要基于以下三点：①其只用判断输入实值是否大于零，而不需要像前文提及的激活函数那样计算指数项，因此运算速度极快；②其在正区间上的导数始终为1，避免了梯度消失与饱和问题；③当输入值为负值时，激活值为零，即该神经元不激活。该模型中的神经元根据输入的不同选择性地被激活，非完全激活的模型引入了稀疏性［15］。稀疏性的引入一方面强化了模型的泛化能力，另一方面减少了一些多余特征。本文还尝试了许多ReLU 的改进版本，如增加光滑性的Swish［16］，其表达式为式（18）；可到达严格梯度下降无法取得的最优值的带噪声的ReLU，表达式为式（19）；加速梯度移动的非饱和ReLU，例如Prelu［17］，其表达式为式（20）。为了在工程上快速实现，最终选择Relu 作为网络结构中的激活函数。图2 给出了ReLU 与Swish 激活函数的示意图。

Fig.2 ReLU and Swish activation functions图2 ReLU 与Swish 激 活 函 数

1.4 批量规范化

内部协变量转移（Internal Covariate Shift，ICS）现象影响了模型的非线性表达能力，因此引入批量规范化（Batch Normalization，BN）进行抑制。该方法将小批次数据标定为拟正态分布，并通过具有学习性的重构参数γ和β恢复学习到的特征。加入BN 后，优化器不必再小心调节学习率和初始化参数，在很多情况下，也不再需要正则项［18］。本文在设计网络架构时将BN 层加入到卷积层与激活层之间，在下一层卷积运算前进行BN 处理，更有利于保留训练图像中的先验信息，使不具备稀疏分布特征的映射规范化后，每一层的输入输出分布更加稳定。可将BN 的规范化操作表示为以下公式：

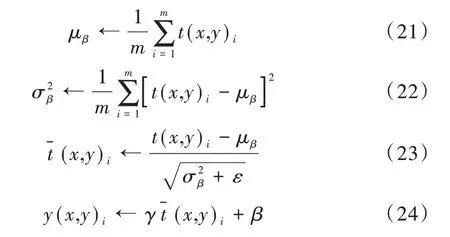
式中，i为数据中每个样本的序号，t(x,y)i为每个BN 层的输入图像数据分别为输入图像矩阵对应点的均值与方差。为防止分母为零，引入极小量ε，γ和β在反向传播中得到更新。

1.5 跳跃连接

深度CNN 通过神经层的堆叠将图像的低级与高级特征串联起来。深层网络提取的抽象特征更具备语义信息，增大了假设空间，故而越深的网络往往表现出越优的性能，但是深层网络带来的梯度消失与爆炸问题妨碍了模型的收敛及更优性能的体现。如果直接使用正则化层解决这个问题，深度网络在训练过程中很容易出现损失值先减小后反弹的现象，即出现退化问题［19］。因此，本文将浅层特征通过跳跃连接与深层特征融合，以改善深度网络参数难以优化这一问题。残差结构如图3 所示，用数学式可表示为：

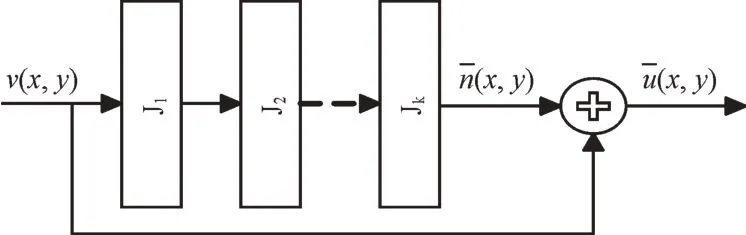
Fig.3 Residual structure图3 残差结构

式中，v(x,y)经过k个卷积层与激活层映射为负的预测噪声图像与之和即为残差块的输出。

1.6 网络整体架构

结合非对称多尺度卷积的降噪CNN 模型整体结构如图4 所示。

Fig.4 ACCNet overall architecture图4 ACCNet 整体架构

（1）第1 层为卷积操作，意在对输入图像进行初步滤波处理，平滑了明显的噪声点。

（2）第2 层为ACCB，其内部为5 个不同尺度的卷积操作和Relu 激活，然后经过Concat 连接，输出为一个有256 个通道的特征图，使第1 层输出的64 通道特征图变换为特征更丰富的256通道特征图，同时增加了不同感受野上的输出。

（3）第3 层为Conv+BN+ReLU，该层对上一层256 通道的张量进行特征融合，回归到64 通道的特征图。

（4）第4-14 层的每层均为Conv+BN+ReLU 的组合，通过卷积操作与ReLU 激活的交替堆叠，组成了复杂的非线性模型，以便学习到良好的降噪映射。

（5）第15 层为卷积层，其输出与模型的输入进行跳跃连接，形成残差结构，从噪声图像中抽离干净图像作为模型最终降噪结果。

上述模型除了ACCB 中使用了非对称多尺度卷积核，以及第1、3 和15 层分别使用了64 个单通道、64 个256 通道以及1 个64 通道3×3 的卷积核外，其余卷积层均为64 个64 通道3×3 的卷积核。

1.7 网络训练优化算法

选取随机梯度下降法（Stochastic Gradient Descent，SGD）与自适应矩估计法（Adaptive Moment Estimation，Ad⁃am）优化网络。SGD 是经典有效的优化算法，但选择合适的学习率较为不易。Adam 优化器是一种基于适应性低阶矩估计的对随机目标函数执行一阶梯度优化的算法，其结合了AdaGrad 优化器与RMSProp 优化器的优势，使得模型收敛速度更快、对内存要求更低，也不需要困难地调节超参数［20-21］。在初步架构模型阶段，先使用Adam 优化器快速确认最优模型的大致结构，然后使用SGD 训练确定模型的最优权值和最优偏置值。本文建立的损失函数为均方误差，符合峰值信噪比的计算思想，其中损失函数可表示为：

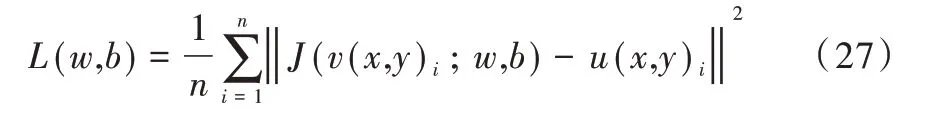
式中，n为每个小批次设置的训练样本数量，i为小批次样本中每个图像数据的序号，J(v(x,y)i;w,b)表示模型输出，u(x,y)i为相应标记的干净图像。

将每个批次样本数量n设置为128，计算样本的整体损失，然后使用梯度下降法优化参数，其中权重更新可表示为：

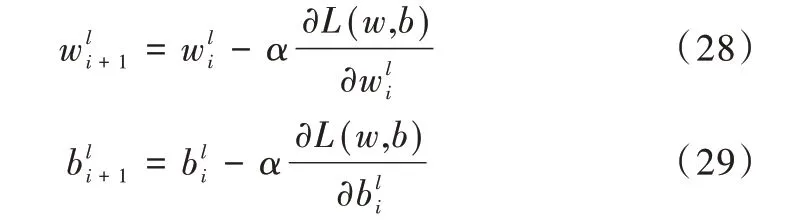
式中，l为当前降噪网络的层数编号，i为权值的迭代次数，α为学习率。设置初始学习率为0.01，经过100 个Epoch指数后下降到0.000 01。

2 实验结果与分析

2.1 训练集与环境

参照文献［10］，使用CBSD400 训练降噪模型，其包含400 张尺寸为180×180 的灰度图像。通过数据增强将400张图像旋转剪裁成128×2 109 张分辨率为40×40 的子图像。为了训练模型并测试其降噪性能，对图像加入均值为零，标准差分别为15、25 和50 的高斯噪声，以便训练出能够应对不同噪声水平下降噪任务的参数。

模型的训练与测试在Keras 深度学习框架下由GPU 加速实现。该框架以TensorFlow 与Theano 为后端，能够在不失灵活性的前提下快速实现。计算硬件配置为Intel（R）Xeon（R）CPU X5670 @ 2.93GHz，NVIDIA GeForce GTX 1070 8G，RAM 为16G，系统驱动为Windows 10 64 位下的cuda9、cudnn7。超参数Batch Size 设置为128，训练100 个Epoch，每个Epoch 训练2 109 个Batch 样本数据。

2.2 ACCB 结构对模型性能的影响

为探究ACCB 与其他常见结构降噪性能的差异，将ACCB 替换到不同尺度正方形卷积核中进行对比实验。如图5 所示，共进行3 组实验，分别为ACCNet、尺度为7 和9 的正方形卷积核替换ACCB 结构的网络模型，测试降噪图像与干净图像的峰值信噪比。结果表明，ACCB 结构优于对称的大尺度卷积核。

Fig.5 Comparison of ACCB and symmetric convolution图5 ACCB 与对称卷积对比

不同的非对称多尺度结构对模型降噪性能有一定影响。为找到适合本文架构的非对称多尺度结构，以下考察几种不同的非对称多尺度块。如图6 所示，从左到右依次记为ACCB、B、C、D，其中B 使用了尺度为3、5、7 和9 的对称卷积核进行并行处理，C 为非对称卷积核替换B 的正方形卷积核，D 为横向与纵向的非对称卷积串联替换B 的正方形卷积核。如图7 所示，平衡了感受野大小与参数量的ACCB 使得模型具有良好的降噪能力，在客观评价标准PSNR 上表现最佳。

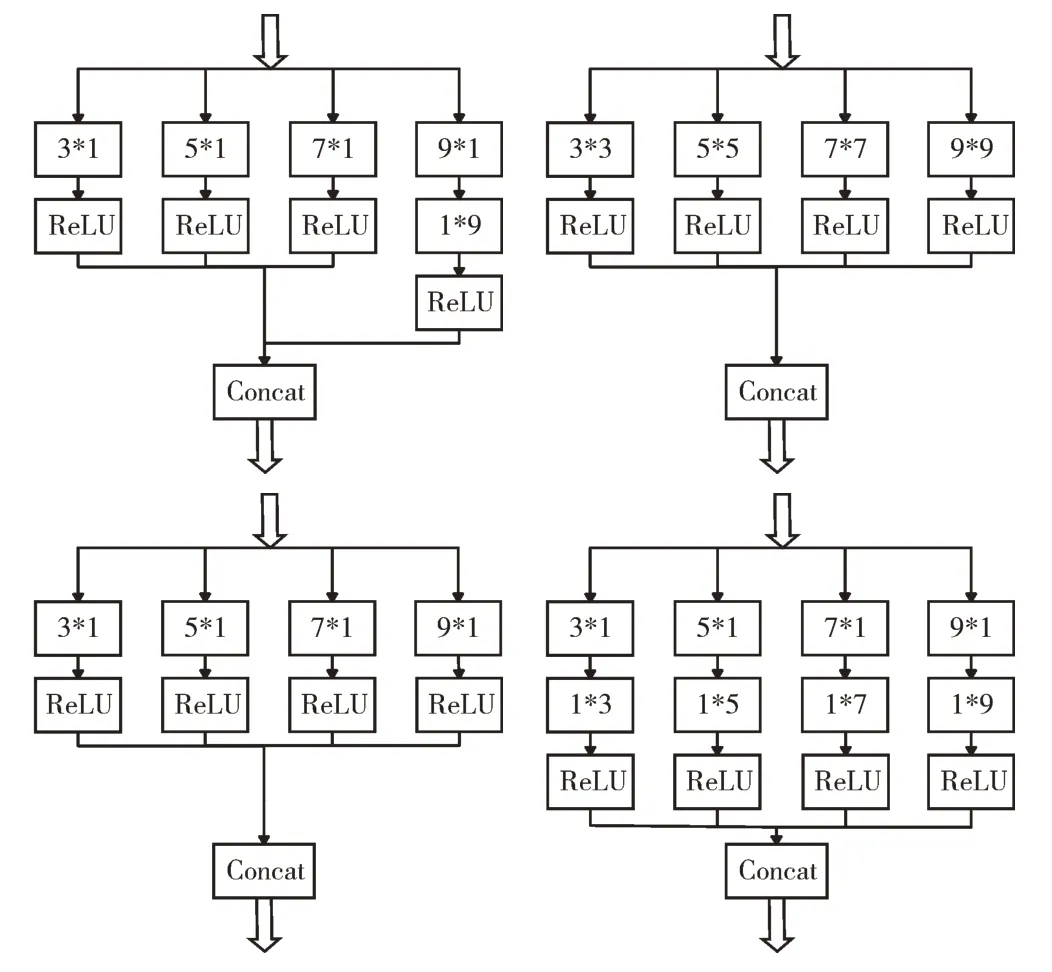
Fig.6 Several different asymmetrical multiscale structures（ACCB，B，C，D from left to right）图6 几种不同的非对称多尺度结构（从左到右依次为ACCB、B、C、D）

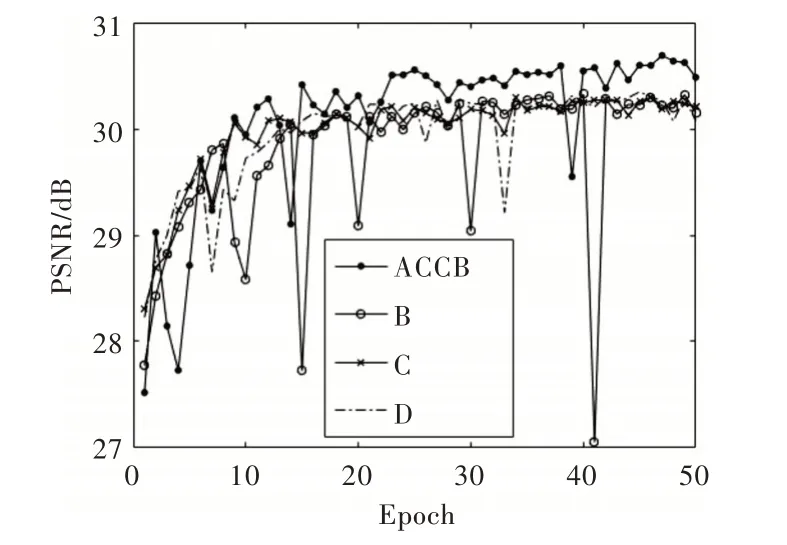
Fig.7 Comparison of different ACCB performance图7 不同ACCB 性能对比

2.3 RL 和BN 对模型性能的影响

如图8 所示，通过对比残差学习RL、批量规范化BN 与ACCB+BN+RL 的降噪网络可知，ACCB 与残差学习RL、批量规范化BN 有着相辅相成的作用，三者的联合作用使得降噪网络能快速收敛且降噪表现最佳。

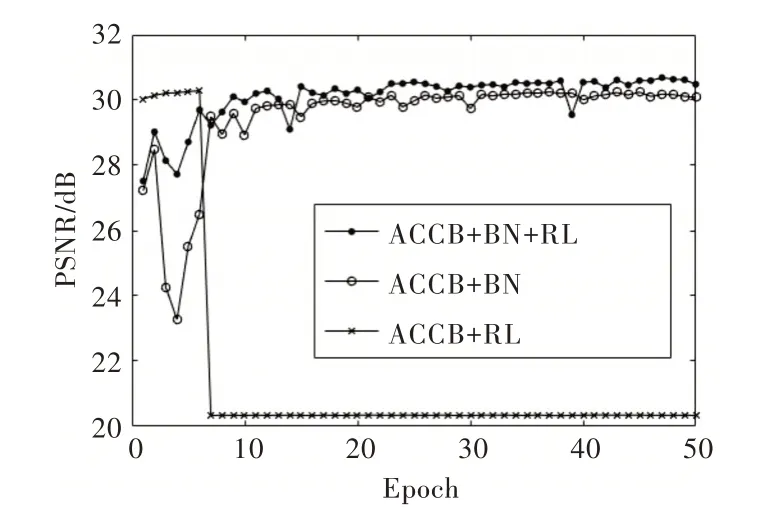
Fig.8 The impact of RL and BN on model performance图8 RL 和BN 对模型性能的影响

2.4 与其他模型比较

为进一步体现ACCNet 的有效性，采用常用测试集Set12，在噪声强度分别为15、25、50dB 的情况下将其与几种算法进行标准峰值信噪比的比较。从表1 可以看出，ACCNet 在强弱噪声下均能很好地对含噪图像进行降噪。与经典算法BM3D 相比，ACCNet 在3 种噪声强度下的峰值信噪比均值分别高出了0.736、0.675、0.698dB。与最新的深度前馈降噪网络DnCNN 相比，ACCNet 的峰值信噪比均值也分别提高了0.249、0.208、0.242dB，并且对大部分图像均有较好的降噪效果。图9 给出了干净图像、含噪图像与噪声水平为25dB 的图像经过ACCNet 模型降噪后的拼接图像。从视觉感受上来说，原始图像与降噪图像相差无几，该模型在降噪的同时较好地保留了图像的边缘细节，没有过多模糊。

Table 1 Comparison of PSNR results of different algorithms under three noise cevels表1 3 种噪声水平下不同算法峰值信噪比的比较结果 单位：dB

Fig.9 Noise reduction effect at 25dB level of ACCNet图9 噪声水平25dB 时ACCNet 的降噪效果

3 结语

研究结果表明，图像噪声在复合感受野结构中能良好地被抽离出来，非对称卷积在降低网络复杂度的同时也不会影响降噪网络的精度。ACCNet 对图像边缘细节具有良好的识别能力，可以预测该网络模型也适用于图像识别、边缘检测、图像分类、图像去模糊等任务。ACCNet 的网络复杂度与DnCNNs 网络相当，但在峰值信噪比均值上优于DnCNNs。不足之处在于，ACCNet 对个别图像的降噪效果不佳，即泛化能力有待提高。在后续研究中，将会采用更大的训练集，并展开对特定含噪图像的降噪研究，以便在一定条件下对降噪效果不佳的图像进行修正，解决ACCNet泛化能力不强的问题。