基于人群队列模型的高校毕业生趋向大数据分析方法研究

刘纪敏，谢创森，文龙日，赵慧奇，王心刚，贾全秋，宋明浩

（1.山东科技大学智能装备学院；2.泰山科技学院 大数据学院，山东泰安 271000；3.吉林省延边第一中学，吉林 延吉 133000）

0 引言

根据教育部发布的2019 年全国教育事业发展统计公报，2019 年全国共有各级各类学校53.01 万所，比上年增加1.13 万所，增长2.17%；各级各类学历教育在校生2.82 亿人，比上年增加660.62 万人，增长2.40%［1］。中国高校毕业生数量快速增长，不仅将影响人力资源供需结构，而且因其对高校教学辅助资源的需求迅速增加，为高校带来了沉重压力。近年来，大部分高校毕业生选择通过研究生考试获得更多深造机会，而选择深造和选择就业的毕业生对教学辅助资源的需求是截然不同的。从高校的角度来看，有必要正确理解在校生需求，并有效应对毕业生就业趋向的变化。根据毕业生就业趋向分析结果，合理分配现有教学辅助资源以满足在校生需求对高校的长远发展具有重要意义［2］。

在教学辅助资源分配相关研究中，Ho 等［3］提出利用综合多准则决策分配资源以提高高校绩效的方案，马瑞华［4］提出地方综合性大学分配学术资源的最佳策略，Zhang［5］提出利用误差反向传播（Back Propagation，BP）神经网络（Arti⁃ficial Neural Networks，ANN）模型解决高校思想政治教育资源的配置问题，还有一些专家利用数理统计和问卷调查方法分析毕业生就业趋势和高校教学辅助资源的合理分配问题［6-7］。虽然很多专家一直利用不同分析方法研究有效的教学辅助资源分配方案，但其所利用的分析方法工作量大，且敏感性与准确性不佳。

自1939 年Forst［8］提出从年龄、时期和队列3 个维度研究结核病数据分析方法后，人群队列（Age Period Cohort，APC）分析模型已广泛应用于各领域的数据分析。如Pes等［9］利用人群队列模型分析社会经济转型后人群患癌症年龄段的变化趋势；Stanesby 等［10］利用人群队列模型调查分析1950-1980 年澳大利亚妇女的饮酒趋势；石超等［11］利用分层人群队列随机效应模型（Hierarchical APC-Cross Clas⁃sified Random Effects Model，HAPC-CCREM）分析中国人对生活的满意度；Wong 等［12］利用人群队列模型分析香港年青一代对政府政策的满意度。研究结果表明，人群队列模型非常适合基于大数据的预测分析。将人群队列模型应用于人群大数据分析有很多优点，但是年龄、时期和队列三要素存在完全线性关系，即时期等于年龄与队列的和，因此模型矩阵是非满秩奇异矩阵，而且是不可逆矩阵，所以存在不可识别的问题。针对该问题，不少专家提出改进的人群队列模型［13-14］。

本文收集了山东科技大学近10 年的毕业生信息，并利用人群队列模型进行毕业趋向大数据分析。在研究初期，通过数据分析人群队列模型中的三大要素，即年龄、时期和队列，在时间跨度不大的前提下，实验结果并不理想。为提高实验结果的准确性，本文不仅对收集到的毕业生数据进行特征分析，而且同时进行了毕业去向相关问题的线上问卷调查。通过调研与分析发现，即使时间跨度不大的因子也会对结果造成较大影响。例如，年龄比毕业生平均年龄大的学生更倾向于选择就业，还有国家政策的改变与性别对实验结果也有一定影响。综合这些影响因素和研究目的，最后提出改进的人群队列模型和人群队列大数据分析模型。最终实验结果表明，本文提出的模型适用于高校毕业生毕业趋向分析，可为合理分配教学辅助资源提供参考依据。

1 人群队列模型

人群队列模型是人群队列调查的基本模型，包括年龄、时期和队列3 个因素。由于这3 个因素之间存在完全线性关系，所以利用传统回归方法无法获得唯一的估计值。为解决该问题，需要改进人群队列模型特征参数选取方法以及使用内在估计方法计算参数，并使用元数据映射方法导入变换的数据。以下首先提出传统人群队列模型存在的问题，然后定义毕业趋向影响因素，最后定义分析模型影响因素。

1.1 传统人群队列模型

在泊松回归（Poisson Regression，PR）模型基础上，人群队列模型如今已广泛应用于数据调查领域［15-16］。通过前期研究发现，传统人群队列模型非常适用于高校毕业生就业趋向大数据分析。

传统人群队列模型基本公式如下：

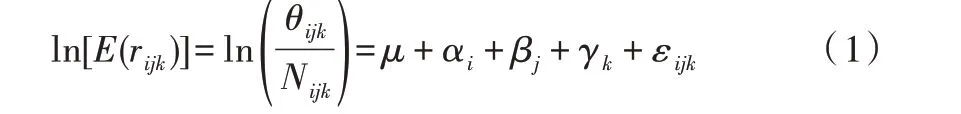
式中，E(rijk)是基于年龄（i）、时期（j）和队列（k）的疾病发病可能性期望值，θijk是第j个时期观察到的第i个年龄组疾病发病可能性期望值，Nijk是对应年龄、时期和队列的人数，μ是年龄、时期、队列作用的趋势参照值，αi是第i个年龄组群的影响（i=1，2，3，…，i），βj是第j个时期组群的影响（j=1，2，3，…，j），γk是与第i个年龄组和第j个时期组参数相关第k个队列组的影响，εijk是随机误差。

在人群队列模型中，传统最小二乘估计方法b=(XT X)-1XTY存在一个“无法估计”的问题。由于年龄、时间和队列之间存在完全线性关系，即时间值等于年龄加上队列，该矩阵是一个非满秩奇异矩阵且是不可逆的，因此b没有唯一的结果。此外，传统人群队列模型以5 年为间隔对样本数据进行测试，虽然实验结果可反映大概的毕业趋势，但不能代表5 年时间间隔之间的变化，因而缺乏对测试的敏感性。在传统的人群队列模型中，只分析年龄、时期和队列因素的影响，如果影响因素更多，将降低实验结果的准确性。因此，本文提出改进的人群队列模型以解决这些问题。

1.2 毕业趋向影响因素

本文利用从山东科技大学就业指导中心收集到的2011-2018 年毕业生毕业趋向信息建立样本数据模型，并定义了高校毕业生毕业趋向影响因素，如表1 所示。

Table 1 Definition of influencing factors of graduation trend表1 毕业趋向影响因素定义

在影响因素中，“深造”表示申报研究生考试或留学读研的毕业生，“就业”表示参加工作或参加公务员考试的毕业生，“其它”表示参军或待业的毕业生。另外也考虑了可能影响实验结果的因素，如性别、国家政策等。

虽然研究中采用的样本数据可满足Li 等［17］提出的人群队列模型对样本数据的要求，但是年龄较大的高校毕业生更倾向于选择就业的趋势等影响实验结果的情况也不能忽略。为更明确地对毕业趋向进行可视化展示，将样本数据中的年龄替换成以5 年为间隔的年龄段，通过对年龄的扩展以便于开展毕业趋向分析实验，同时可避免出现实验结果不明确的情况。

1.3 分析模型影响因素

毕业生毕业趋向分析结果表明，年龄对毕业趋向的变化影响最大，其原因可能是不同年龄在生理上的需求以及对社会地位的重视程度不同；时期通常反映在纵向分析中，并且影响所有年龄段；队列表示相同事件。

（1）年龄因素。从样本原始数据分析中发现，毕业生选择工作而不是接受进一步的教育（p<0.01），并且这种状况影响了毕业生深造趋势。

在过去的调查中，通常将年龄以5 年为间隔划分成一个队列组，用来分析年龄对毕业趋向的影响［18］。通过实验，以5 年为基础的年龄划分弱化了年龄差距对结果的影响，例如同一年毕业生在年龄相差为两岁的情况下往往有着截然不同的选择，如某年实施的某种政策极大地增加了研究生数量等，从而大大降低了结果的准确性。为了合理使用样本数据，将年龄映射到5 年的范围空间中，并将属性划分为以下人群队列，如表2 所示。

Table 2 The range of actual age in the experiment表2 实际年龄在实验中的对应年龄段

同时，还需要更改相应出生队列，以保持年龄、时期和出生队列3 个因素之间原本的线性关系。确定年龄因子的值，并与表达式中的原始数据加以区别。

（2）时期因素。在提出的人群队列模型中，周期因子的效果尤为明显。每一年政策和改革等不稳定因素都会对结果产生较大影响。例如，某政策在某年的实施极大地增加了研究生数量，因此以5 年为基础的时期队列划分方式会严重影响结果的准确度和灵敏度。以5 年为间隔进行时期划分，如表3 所示，但这5 年间隔仅用于实验与结果分析，对结果没有影响。

Table 3 The corresponding period of actual period in the experiment表3 实际时期在实验中的对应时期

（3）队列因素。为了提高结果的准确度，将年龄和时期因素分别映射到5 年间隔中。由于同类群组值的线性关系等于周期减去年龄，因此同类群组值已更改。在先前的数据映射之后，每个更改的队列对应于表4 中给出的一年的原始数据。

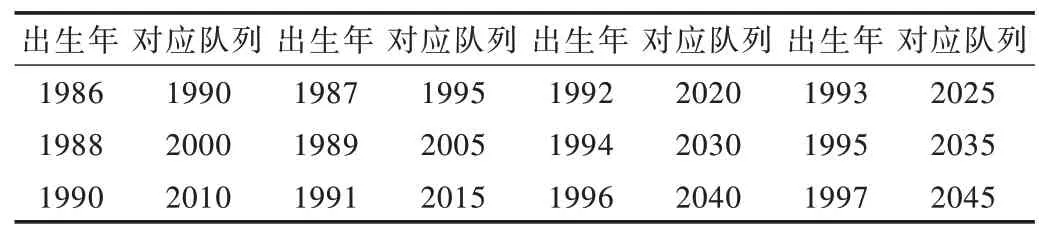
Table 4 The corresponding cohort of actual cohort in the experiment表4 实际队列在实验中的对应队列

在前瞻性队列分析中，将映射到5 年区间内的对应关系继续应用于新模型中，以避免因数据不统一导致的意外错误。

2 人群队列大数据分析

为解决传统人群队列模型“无法识别”的问题，采用内源估计法（Intrinsic Estimator，IE）对参数进行估计。IE 方法是基于Fu［19］的估计函数方法提出的，Yang 等［20］将IE 方法与传统的广义线性方法进行比较，发现其输出结果相似。IE 方法具有无需假定先验信息的优点，但由于其参数存在难以解释的问题，因此尚未得到广泛应用。

为解决传统人群队列模型“低灵敏度”的问题，研究者们又提出一种数据映射方法，将原来的1 年数据扩展为5年数据，从而确保输入数据的正确性，并分析随机年份中可能发生的情况（可保证数据符合模型标准，并分析任意一年可能发生的变化）。人群队列大数据分析模型利用Stata15 和Python 进行实验，并根据实验结果提出毕业趋向分析方法和教学辅助资源分配方案。

2.1 毕业趋向分析方法

基于人群队列大数据分析模型的不同年龄毕业生毕业趋向分析结果如图1 所示。

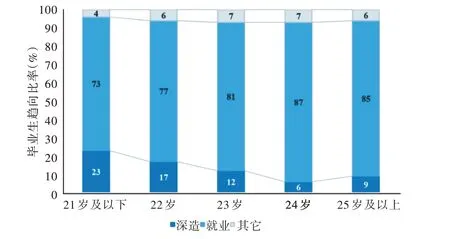
Fig.1 Analysis results of graduation trend of graduates of different ages图1 不同年龄毕业生毕业趋向分析结果

在分析结果中，各年龄阶段毕业生选择“其它”（在表1中变量值定义为0）选项的变化不大且占比较低，选择“深造”（在表1 中变量值定义为1）选项的大多是年龄较小的毕业生，且毕业生样本数量不同会影响毕业趋向分析结果，选择“就业”（在表1 中变量值定义为2）选项的大多是年龄较大的毕业生。

基于人群队列大数据分析模型的毕业生深造趋势分析结果如图2 所示。

Fig.2 Analysis results of graduates'further study trend图2 毕业生深造趋势分析结果

在就业蓝皮书中提到，深造已成为本科毕业生的热门选择之一。深造分为全日制和非全日制，自2017 年起，政府部门表示两种学历在中国具有相同的法律地位。因此，从2017 年开始，越来越多高校毕业生选择深造。但由于竞争比以前更激烈，2018 年选择深造的人数又呈下降趋势。

基于人群队列大数据分析模型的毕业生就业趋势分析结果如图3 所示。

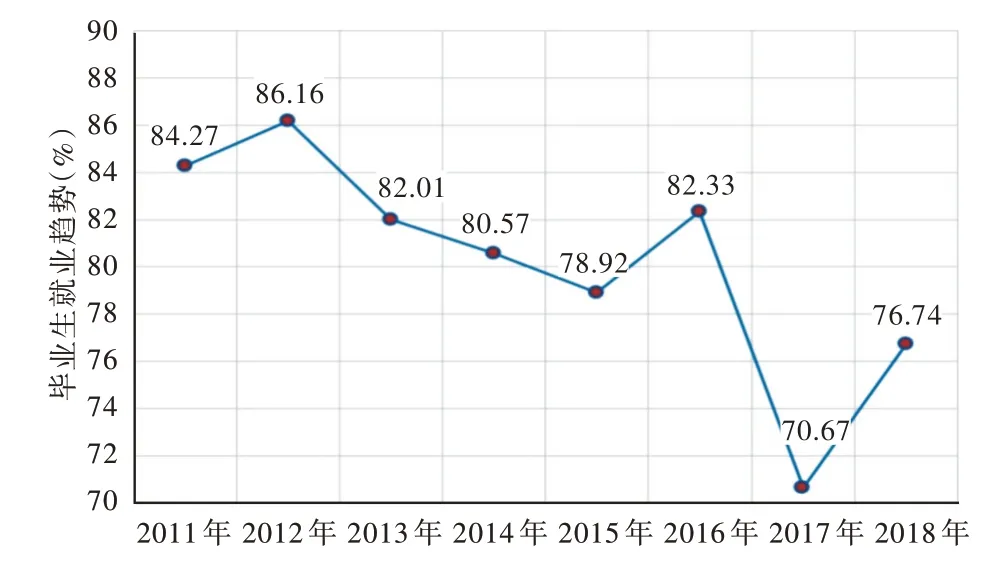
Fig.3 Analysis results of graduates'employment trend图3 毕业生就业趋势分析结果

2017 年考研政策的修改导致一部分毕业生改变了原有想法而选择继续深造，因此2017 年选择就业的毕业生数量呈明显下降趋势，但随着竞争的加剧，2018 年就业人数有所回升，但占比仍低于往年。

基于人群队列大数据分析模型的不同性别毕业生毕业趋向分析结果如图4 所示。

Fig.4 Analysis results of graduation trend of graduates of different genders图4 不同性别毕业生毕业趋向分析结果

分析结果显示，女生相比男生更趋向于深造，但大多数毕业生仍然选择了就业。

2.2 改进的人群队列模型

使用IE 参数估计方法可得到影响因子队列，但不能将政策的影响与具体时期分离开。为定义政策因素对结果的独立影响，基于式（1）提出政策因素计算方法，如式（2）所示。

首先输入不同时期的样本数据，然后根据人群队列模型计算3 年的平均值，最后从偏差结果中得出政策因素的值。为了表示数据映射，将式（1）修改为式（3）。使用变量A、B、C 分别代表年龄、时期、队列实际值与映射值之间的对应关系。

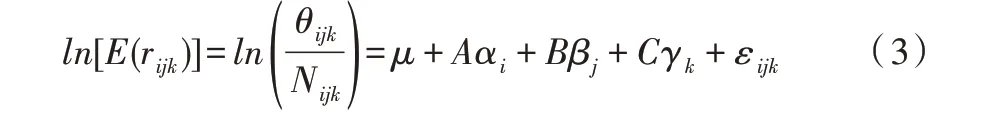
为进行前瞻性的队列分析，将每一年的政策因素和性别因素加入式（3）中，提出最终模型，如式（4）所示。

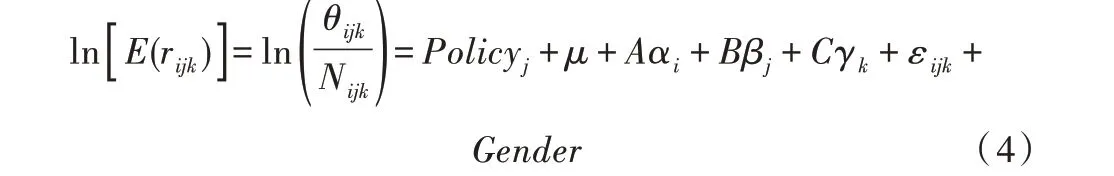
2.3 基于改进人群队列模型的毕业趋向分析

基于改进人群队列模型的毕业趋向分析实验结果如表5 所示。

Table 5 Results of graduation trend analysis based on improved cohort model表5 基于改进人群队列模型的毕业趋向分析结果

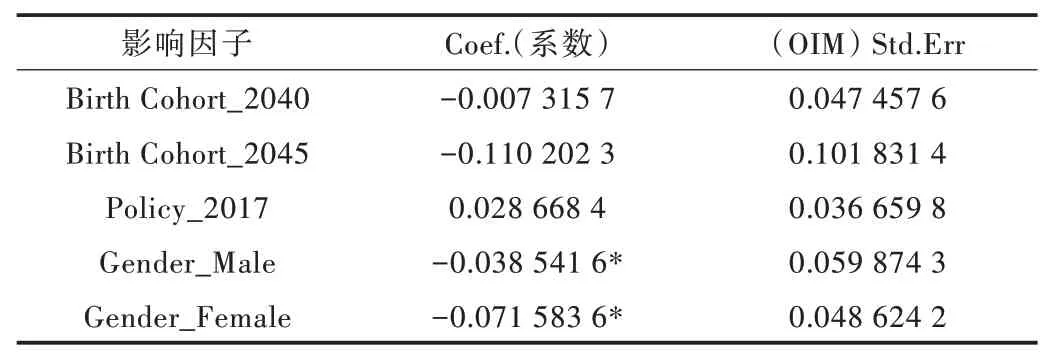
注：*** p <0.000 1，** p <0.001，* p <0.05；（OIM）Std.Err：Coef 系数方差平方根，Coef 的计算基于最大似然估计中的观测信息矩阵

从分析结果可以看出，年龄因素对结果会产生不同影响。同时，即使是较小的年龄差也会对结果产生较大影响。正向的Coef 表示毕业生们更倾向于选择“就业”和“其它”，负向的Coef 表示毕业生们更倾向于选择“深造”。

从整体上看，随着年龄的增加，Coef 值呈上升趋势，意味着年龄大的毕业生更倾向于选择“就业”或“其它”而不是继续深造，但在Age_30 中发生了较大变化，主要因为在中国极少有年龄为25 岁及以上的毕业生，样本数量的缺少导致了结果的偏差。

从Period_2050 所对应的Coef 中可以发现，Coef 的变化相对较为随机且难以预测，表明包括政策因素在内的众多因素都会对Coef 系数产生影响。因此，在前瞻性队列分析中，将政策因素从时期队列因素中分离出来会极大地提高预测的准确性，但其它影响因素还需要继续调查。

从出生队列的Coef 变化来看，数据结果呈现先增加、后减少的趋势，其清晰反映了近几年中国毕业生选择趋势的变化，而Birth_1990 出现了与规律相悖的变化，也是由于样本数量不足，导致结果出现了偏差。

但本文提出的模型中将结局变量定义如下：“深造”为0，“就业”为1，“其它”为2。所以在相同情况下，结果可能会产生较大偏差。

在改进的人群队列模型实验中，年龄对实验结果的影响如图5 所示。由图可见，随着年龄的增长，Coe（f系数）整体呈上升趋势，但在25 岁后逐步降低，表示毕业生随着年龄的增长更倾向于就业而不是深造，而25 岁所呈现的下降趋势是受到样本数量限制而导致的结果偏差。

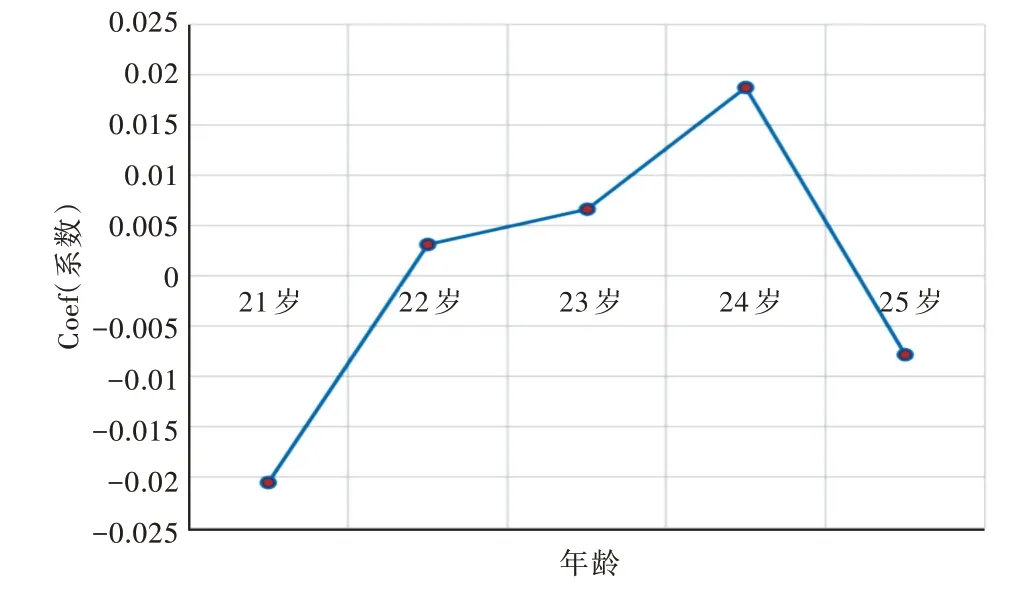
Fig.5 Effect of age on the experimental results图5 年龄对实验结果的影响

在改进的人群队列模型实验中，时期对实验结果的影响如图6 所示。时期队列因素主要受重大事件或政策的影响，此外也与该年的教学氛围及学生质量有关。2017 年，由于国家有关研究生入学考试政策的出台，大量毕业生选择继续深造。但随着竞争的愈加激烈，导致学生对深造的热情下降，因此2018 年选择深造的人数又呈下降趋势。

Fig.6 Effect of the period on experimental results图6 时期对实验结果的影响

在改进的人群队列模型实验中，出生队列对实验结果的影响如图7 所示。出生队列代表一个经历了相同社会变化的群体，可反映出年龄与时间对结果造成的综合影响。由于样本数据中的双极数据（例如1986 和1997 出生队列）较少，因此结果可能存在偏差，但整体呈下降趋势，表示越来越多毕业生选择继续深造，中国的教育水平正在发生变化。

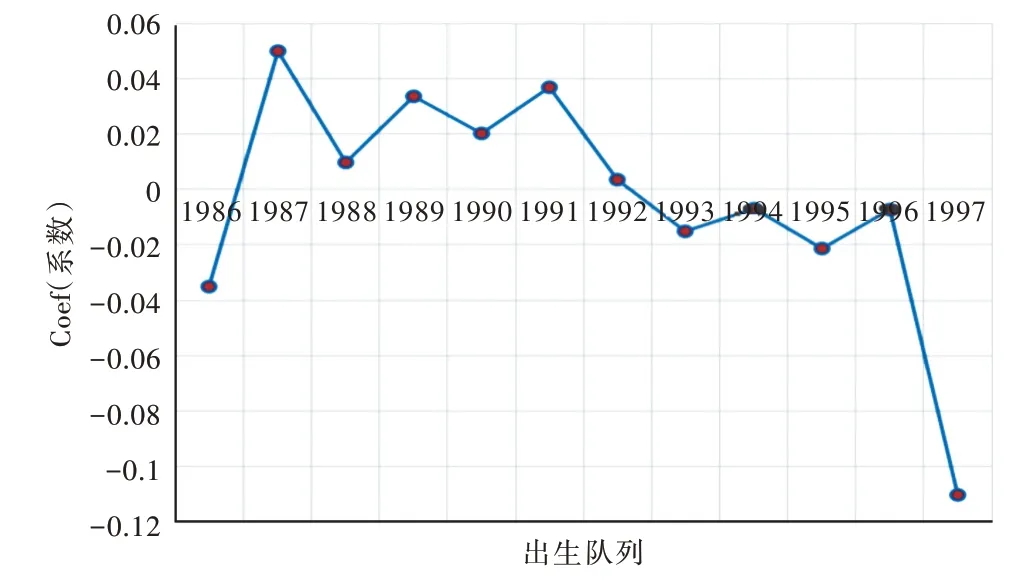
Fig.7 Effect of birth cohort on experimental results图7 出生队列对实验结果的影响

2.4 教学辅助资源分配方法

毕业趋向可利用年龄、时期、队列进行分析。根据基于人群队列模型的前瞻性毕业趋向大数据分析实验结果，不仅可更加合理地制定教学辅助资源分配方案，而且可根据毕业趋向提前为在校生分配不同的教学辅助资源。例如，当“深造”呈上升趋势时，可合理分配考研科目相关的教学辅助资源；当“就业”呈上升趋势时，应增设相关培训机构或开设更多实践类课程；对于选择“其它”的毕业生，可联系相关部门进行针对性的教育培训。人群队列模型可帮助高校更加精准地预测在校生毕业趋向，从而提前合理调配教学辅助资源。

3 实验结果分析

Ho 等［3］使用层次分析法（Analytic Hierarchy Process，AHP）确定拟议项目相对于大学目标的优先级或相对重要性，并使用目标计划（Goal Programming，GP）模型选择最佳项目集。马瑞华等［4］采用文献法、调查法和案例分析法相结合的理论与研究方法，提出一种用于教学辅助资源分配的新方法。在提出的人群队列模型中，通过将数据映射到人群队列模型的5 年区间中，以提高影响因子对结果的敏感性。因为模型针对的是学生群体，所以通过毕业趋向大数据分析可对教学辅助资源进行合理分配，以避免资源浪费。

本文提出的人群队列模型与GP 模型以及MA（马瑞华）模型的性能比较结果如表6 所示。

Table 6 Performance comparison of graduation trend analysis models表6 毕业趋势分析模型性能比较

分析结果显示，本文提出的人群队列模型相比其它模型，在预测难度、测试时间及系统可移植性等方面具有明显改进。

4 结语

随着高校毕业生数量的迅速增加，传统教学辅助资源已无法满足在校生需求。为解决该问题，本文对教学辅助资源分配相关方法和模型进行了调查，并提出毕业生毕业趋势分析方法及改进的人群队列模型。为提高实验结果的准确性和预测结果的适应性，将更多影响因素加入到改进的人群队列模型中。结果显示，本文提出的改进的人群队列模型不仅可清晰地显示毕业趋向，而且可帮助高校更合理地制订教学辅助资源分配策略。随着研究的进一步深入，未来将定义更多影响因素，以期获得更好的预测结果。