量子电路设计软件的框架与实现

郑煜臻，冯加贵，2，熊康林，2

（1.中国科学院苏州纳米技术与纳米仿生研究所纳米真空互联实验站；2.材料科学姑苏实验室，江苏 苏州 215123）

0 引言

超导电子电路在量子计算与量子测量中有重要应用［1-2］。在分析超导量子电路时，需要考虑其所有节点的状态，通常节点状态不用电压和电流表示，而是用共轭变量磁通（电压的时间积分）和电荷量（电流的时间积分）［3］。对于简单电路，很容易通过将电容器中的静电能与电感器和约瑟夫森结中的磁能相加的方式计算哈密顿量，可采用运算符代替节点磁通和电荷完成量子化［4］。近年来，超导量子电子学飞速发展，目前已有学者提出采用电路量子电动力学研究超导电路与微波之间的相互作用［5］。此外，各种超导量子比特问世［6-9］，其利用电容器、电感器和谐振器实现了量子比特之间的耦合，还实现了量子误差校正。目前62 位的可编程超导量子处理器已成功演示［10］，量子优越性得以证明［11］。

在实际应用方面，纠缠量子比特的质量（通过相干时间和操作保真度衡量）和数量（字面上的个数）仍需提高［1］。为了获得高质量的量子比特，除了改进材料与制造工艺外，还应仔细设计架构，以使其对噪声不敏感［12］，例如Transmon 量子比特添加并联电容器后对电荷扰动的敏感性降低［8］。设计新颖的量子比特是一个耗时、耗资金的过程，为了获得更多耦合量子比特，诸多超导微波元件被集成到同一芯片中，由于电路的复杂性随着元件数量的增加呈指数增长，因此急需一种可以方便设计与分析量子电路的工具［13］。

1 相关研究

超导量子比特的退相干，即波函数坍缩效应，是限制超导量子计算发展的一个难题，主要是由于量子比特会与外界噪声发生耦合［14］。电荷［15］、磁通［16］和相位［17］这3 种典型的超导量子比特分别对环境电荷噪声、磁通噪声和相位噪声十分敏感。为解决这一难题，一方面需要改进材料与制备工艺等降低噪声，另一方面需要从设计上改变超导量子比特的结构，从器件原理出发降低噪声对量子比特的影响［8］。随着超导量子芯片集成规模的快速扩大，量子比特之间的串扰问题变得更加突出［10］，需要系统优化芯片结构，因此优良合理的设计对于提高量子芯片的性能非常关键。

量子芯片的设计跨越多个学科，反馈回路很长，技术上涉及器件布局、器件参数提取、哈密顿量生成、薛定谔方程求解、设计优化等步骤。目前已有用于通用量子模拟的软件，如QuTip［18］、Cirq 和QPanda 等，主要基于矩阵力学设计，关注普适的量子动力学过程，可以辅助量子计算研究，但不能实现量子芯片设计的自动化。近来IBM 发布了专门用于超导量子计算的电子设计自动化软件Qiskit-metal［19］，可对集总元件模型的量子电路进行量子化。其通过调用外部电磁场数值分析软件，对分布式元件进行经典的电磁分析。其还可以基于内建的器件模型和平面芯片结构自动布局布线，但灵活度稍微欠缺。目前，国内尚未发现有公开发布的针对超导量子芯片设计的软件工具。

本文介绍采用Wolfram 语言编写的cQED（Computation⁃al Quantum Electronics Design）软件。相比于采用Python 编写的Qiskit-metal，cQED 可以方便地调用Wolfram 系统的内置几何计算、符号计算和集成数值功能，更适用于复杂超导量子电路的研究。cQED 还可以方便地扩展新功能，整个软件框架无需花费过多精力维护，有望实现量子芯片设计的自动化，并使设计过程高效且不易出错。

2 框架设计

2.1 架构

cQED 软件的框架结构遵循传统半导体芯片物理设计的工作流程：首先需要确定单个电子元器件的几何尺寸，以满足给定的量子特性；然后对电路进行仿真验证；最后将元件放置在芯片上，并布线互联各个元件。此外，在导出用于电路制造的GDSII 版图文件之前，必须多次检查和校验。在cQED 框架下，每个模块都执行特定的任务，用户根据需要可以单独或一起加载相应模块。在Wolfram 系统中，模块也被称为包（Package），“`”符号用作软件包的路径分隔符。例如，cQED`QE`Hamiltonian`表示在cQED 框架的目录QE 下有一个子包Hamiltonian`。在下文中，cQED 将遵循这个惯例。

cQED 的体系结构如图1 所示，主要功能以矩形框的形式列出，即文件系统中的目录。每个目录下都有数个源文件，每个文件都包含一个子包的定义，每个子包都有数个公开函数，每个函数可以完成特定任务，当前共有52 个源文件和270 个公开函数。

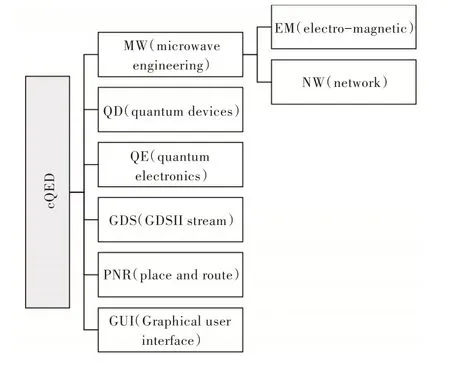
Fig.1 Structure of the cQED framework图1 cQED 软件框架结构

2.2 主要功能

cQED 软件框架主要用于量子计算的超导芯片物理设计流程中，其功能包括量子体系求解、微波工程和布局布线，用户可以单独或同时使用。以下列举每个模块的功能。

cQED 是软件的主体结构，为Wolfram 系统中的用户基础目录，包含cQED`、cQED` UnitsAndConstants`子包以及所有其他模块。其中，cQED 的子程序包控制全局功能，并可获取有关整个框架的统计信息；cQED`UnitsAndConstants`管理输入与输出物理变量和常量的单位。

cQED`MW`包含两个模块，其中cQED`MW`EM`处理电磁问题，并从几何形状中提取电参数，如多个耦合共面波导的电容矩阵；cQED`MW`NW`主要使用散射矩阵法分析微波网络，并可获得耦合到馈线的共面波导谐振器的品质因子。

cQED`QD`包含提取谐振器和量子比特特征的基本工具，还包含了Transmon 在磁通和电荷空间的薛定谔方程的求解。

cQED`QE`用于一般量子电子电路，可以读取电容器、电感器、约瑟夫森结、电流和电压源的网表文件，生成整个电路的哈密顿量。其还可以通过求解定态薛定谔方程给出电路的本征能量和本征矢量，并针对单个节点求解含时方程。该模块的一些子程序包可以绘制电路的拓扑结构和量子态。

cQED`GDS`用于读取和写入GDSII 流格式文件，其可自由操作GDSII 文件。通过使用该软件包，用户可以从Wolfram 脚本中精确地为器件生成几何图案，无需在布局编辑器中手动绘制。

cQED`PNR`用于从逻辑网表中生成布局图，也可以从GDSII 文件中加载量子比特的设计，然后解析量子比特级网表。利用这些网表信息，cQED`PNR`Placing`可以放置量子比特，而cQED`PNR`Routing`可以使用给定长度和宽度的导线连接不同的量子比特。

cQED`GUI`中有数个子软件包，可在用户界面生成带有图形的交互式工具。对于不直接使用代码的人，使用GUI 模块计算某些问题非常方便。该模块也适用于超导量子计算的教学。

2.3 命名规则

从设计方面考虑，cQED 是一个可扩展的软件框架，因此命名规则十分重要。cQED 的几种命名规则为：①私有函数的名称以“r”开头，公共函数的名称以“f”开头；②从另一个程序包调用函数时，始终使用其全名以避免命名冲突；③软件包或模块级别的参数以字母“p”开头，函数内的局部变量以其他小写字母开头；④代码采用过程式编程风格，在cQED 的其他部分，适当时也可使用函数式编程。

3 实现方法

3.1 电磁场模块（cQED`MW`EM`）

超导电路在单个振荡器和耦合组件中广泛使用电容器和电感器等电子元件，电子元器件本身的电磁场值得深入分析。目前有数十种工业软件可用于不同类型的应用场景，但是不适合集成到设计流程中。考虑到目前多在晶片（主要是硅或蓝宝石）上制造超导量子比特和电路，该模块实现了从二维（2D）几何形状中提取电学参数的功能。

cQED`MW`EM`模块解决了3 个问题，均为超导量子器件物理设计的核心。

（1）共面波导和多耦合微带线的电容和电感矩阵。在超导电路中，微波信号在共面波导中传播，一段共面波导可以作为谐振器使用。将不同的波导互相靠近可以有效耦合，使用对称设计和浮动金属接地可以抑制杂散模式，因此TEM 模式或准TEM 模式在这些波导中占主要地位。对于共面波导或微带线，保形映射是首选分析方法，其可使用最少的计算时间提取电容和电感矩阵［20］。

（2）多种金属的电容矩阵。在Transmon 和Xmon 中使用电容器可使量子比特与谐振器之间实现耦合。在超导量子电路中，电容器的尺寸远小于衬底中微波的波长，因此可将电容视为集总元件而不是分布式元件。如果金属形状规则，也可以使用保形映射计算集总电容。然而在大多数设计中，金属形状并不规则，因此需要在三维空间中求解泊松方程。cQED`MW`EM`Electrostatic`子软件包采用数值求解的方法求解静电问题以提取电容，其使用正交网格离散感兴趣的三维区域、设置薄金属电压、求解离散的泊松方程，以获取电势分布。其还利用高斯定律计算每种金属上的感应电荷，最后返回电容矩阵。cQED 软件中使用的网格如图2（彩图扫OSID 码可见）所示，灰色的多边形为薄金属电极，其厚度可被忽略，虚线小框标记红色网格节点的有限体积元。

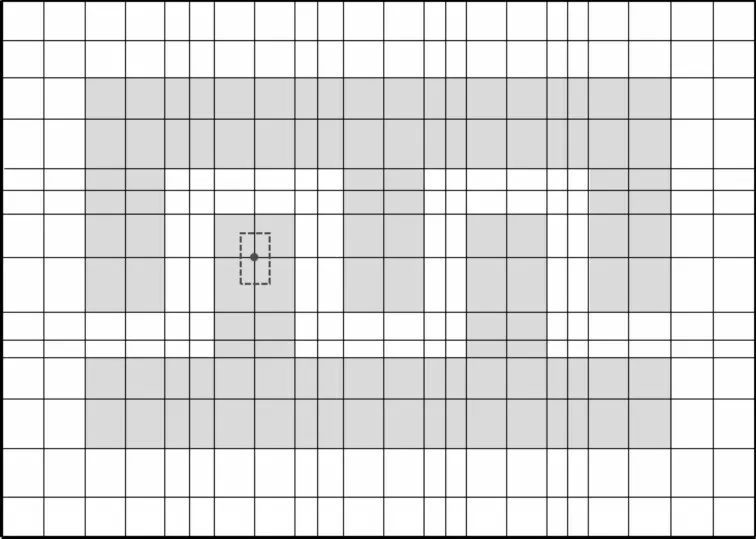
Fig.2 Schematic diagram of the grid on the XY plane to solve the Poisson equation图2 用于求解泊松方程的XY 平面上网格示意图

（3）回路和线路的电感矩阵。在磁通量子比特或Transmon 量子比特中，需要磁通偏置调控SQUID 的有效约瑟夫森临界电流，从而改变量子比特的哈密顿量。此外，一些磁通量子比特也可通过电感耦合，因此有必要计算自感和互感。cQED`MW`EM 模块使用Neumann 公式计算电感［21］。

3.2 微波网络模块（cQED`MW`NW`）

共面波导被广泛用于传导微波脉冲。值得注意的是，由于长度与微波波长相当，波导之间的耦合是分布式的［22］。cQED'MW`NW`模块采用微波网络理论中广泛使用的散射参数分析分布式电路［23］。

本文设计的cQED 软件使用通用模型处理分布式耦合。如图3 所示，N 条微带线相互耦合，其中耦合区域可由S2N×2N矩阵表征。给定耦合区域的长度，通过cQED`MW`EM`模块提取每个单位长度的电容和电感矩阵，进而推导出阻抗矩阵，然后推导S 参数。在给定了某个端口的负载阻抗后，S 参数的秩会降低，从降秩的S 参数中可获得整个网络的信息，如谐振频率等。

Fig.3 Diagram of N coupled metal stripes图3 N 个耦合的金属微带线示意图

该模块的一个特殊应用是计算耦合到馈线的共面波导谐振器的耦合品质因子。例如将1/4 波长谐振器的两个端口分别设置为开路和短路，馈线的两个端口设置为阻抗匹配（50Ω），接地线的端口设置为短路，从馈线的反射或透射谱中可以提取谐振频率以及品质因子。cQED‘MW`NW’模块可分析具有超高品质因子的谐振器，而由于受网格尺寸和数值精度的限制，传统的有限元方法无法模拟该情况。

3.3 量子器件模块（cQED`QD`）

该模块给出了L-C 谐振器和Transmon 的薛定谔方程的解析与数值解。如果是传输线谐振器，可通过找到其等效L-C 电路完成量子化。而对于由电容器C、约瑟夫森结J、电感器L 和并联电流源I 组成的CJLI 电路，通过在相位空间上对薛定谔方程进行数值求解，可以获得本征能量和本征矢量。

若CJLI 电路有两个节点，其中一个节点接地，则CJLI电路的哈密顿量为：

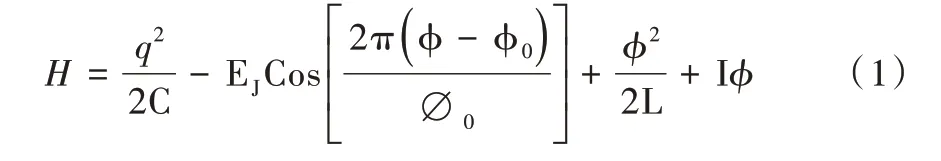
式中，q和ϕ分别为未接地节点的电荷和磁通；C、EJ、L和I 分别为电容、约瑟夫森耦合能量、电感和偏置电流；∅0为磁通量子，而ϕ0为用于调整约瑟夫森结的偏置磁通。需要说明的是，q和ϕ是一对共轭变量，表示为：

将CJLI 电路视为在磁通势阱中振荡且“质量”为C 的粒子，该磁通势阱由感性电子元件决定。约瑟夫森结提供余弦部分，电感器提供抛物线分量，电流源使势阱倾斜。如图4 所示，势阱由约瑟夫森结（左上）、电感器（中上）和电流源（右上）贡献，振荡器的“质量”等于并联电容器的电容。通过在一维相空间中对薛定谔方程进行数值求解，可以获得振荡器的本征能量和本征态。

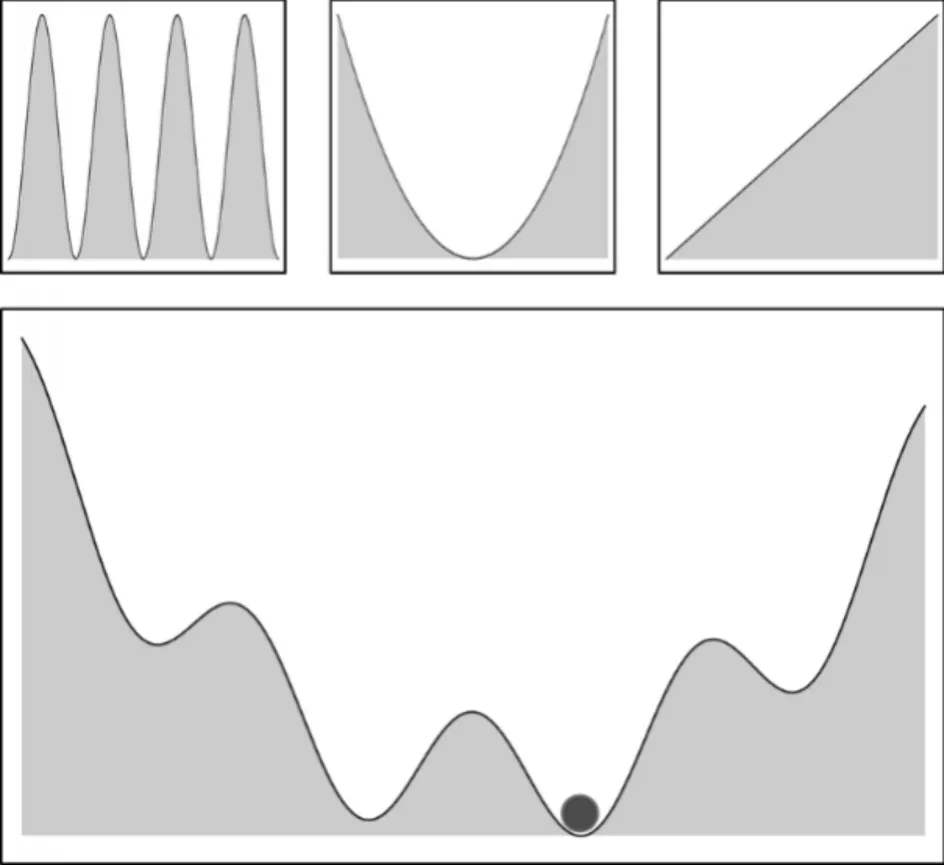
Fig.4 One-dimensional oscillator in flux space图4 磁通空间中的一维振荡器

3.4 量子电路模块（cQED`QE`）

当数个量子比特和谐振器通过电容器、电感器或约瑟夫森结耦合在一起形成电路网路时，网络的哈密顿量会变得复杂。耦合会改变单个器件的哈密顿量，因此在分析器件，尤其是耦合强度较大时，耦合不能被忽略，此时需首先生成整个网络的哈密顿量，然后将哈密顿量分解为各个器件和耦合部分的项。实际上，cQED`QE`模块的功能之一即为大规模网络生成哈密顿量。

该模块通过cQED`QE`Netlist`读取文本文件，获取电路的全局信息。例如，图5 中的电路通过电容器耦合到L-C振荡器的量子比特，电路中有3 个节点，整个电路通过固定格式的文字描述，节点已采用数字编号，其中节点1 接地，节点2 和3 为自由节点。

Fig.5 Equivalent circuit of a Transmon qubit coupled to a resonator by a capacitor图5 通过电容器耦合到谐振器的Transmon 量子比特等效电路

网表加载到cQED`QE`后，将其中一个节点设置为地，默认节点1 接地，则存储在电容器中的静电能量可表示为：

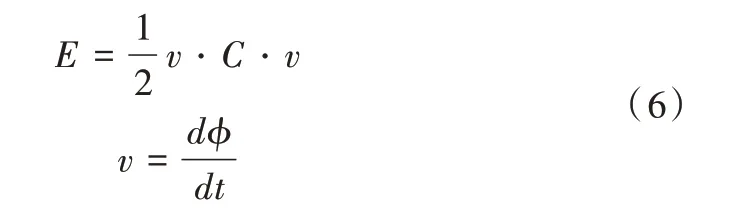
式中，C 为网络的电容矩阵；v为所有节点的电压矢量，其是节点磁通向量ϕ 的时间微分。如果电路中有电压源，则电压矢量v满足：

式中，MV为电压源的邻接矩阵，Vs为电压源的电压。电压源会减少自由节点的数量，该模块在生成电路哈密顿量时将消除非自由节点。

与cQED`QD`模块类似，电路网络中的磁能为电感、电流源与约瑟夫森结中的能量之和。其中，电感能量UL可通过磁通矢量ϕ 和电感矩阵L 计算得到，电流源能量UI为电流源矢量I 与磁通矢量的内积，利用向量EJ、约瑟夫森结的邻接矩阵MJ和磁通矢量可计算得到约瑟夫森结能量UJ，具体表示为：

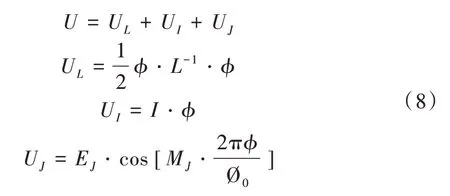
将静电能E 类比为动能，磁能U 类比为势能，电路的拉格朗日量可表示为：

与节点磁通共轭的动量表示为：

式中，q 为所有节点的电荷向量。

联合式（6），节点电压可以用节点电荷表示。如果电路的某些部分是纯电感性的，则节点电压将不会出现在拉格朗日量中，其电荷不能从式（10）中得出，本文cQED 将不考虑该类电路。

采用电荷矢量和磁通矢量表示电路的哈密顿量，为：

如果自由节点的数量，即磁通向量的长度很小，则可在所有节点磁通组成的多维磁通空间中数值求解薛定谔方程。如果自由节点的数量很大，则不可能直接求解薛定谔方程，因为所需内存和计算时间将呈指数级增加。当节点之间的耦合较小时（大多数用于量子计算的电路满足该条件），哈密顿量可表示为：

3.5 文件模块（cQED`GDS`）

GDSII 格式广泛用于存储芯片布局。随着超导量子比特数量的增加，芯片上电路的复杂度呈指数增长。对于具有数千个量子比特的芯片，几乎不可能手工绘制所有器件的几何图形，因此通过脚本操纵超导电路的设计版图至关重要。cQED`GDS`模块可用于读取、写入和修改GDSII 文件。

如图6 所示，cQED`GDS`模块是根据GDSII 流格式的数据结构实现的。GDSII 为二进制文件格式，其记录列表以预先定义的顺序存储。每个记录都包含头文件和特定类型的数据。若要读取GDSII 文件，第一步是将原始二进制数据转换为GDSII 可以识别的数据类型；在记录时，GDSII由实体数据结构组成，因此第二步是将记录放入实体中，并根据一定的关系排列实体；最后一步是访问实体中的数据。除了读取、写入和修改GDSII 文件外，该模块中的cQED`GDS`Graph`软件包可将GDSII 元素转换为图形基元并进行显示，cQED`GDS`Shape`子包可用于生成超导芯片中的常用图形。

Fig.6 Data structure and functionalities of the cQED`GDS`module图6 cQED`GDS`模块的数据结构与功能

3.6 布线模块（cQED`PNR`）

超导芯片的规模在不断扩大，cQED`PNR`模块旨在实现超导芯片布局图形的自动生成。该模块可处理量子比特的放置以及二维平面上的布线，目前不考虑二维以外的技术，如倒装芯片键合和三维封装。布局和布线是CMOS芯片物理设计的重要步骤，其可以从门级网表和标准单元中生成芯片布局。门级网表定义电路的逻辑功能，简单电路可以通过手动创建门级网表，大型电路的门级网表可以在逻辑综合步骤从寄存器传输级网表中自动生成；标准单元是已验证和制造的基本逻辑单元的物理布局。在超导量子计算中，网表是量子比特级的，而标准单元是量子比特的图形。cQED`PNR`网表用于解析量子比特级的网表，网表的语法类似于Verilog 硬件描述语言。

读取量子比特级的网表后，实例量子比特之间的逻辑连接可清楚地用邻接矩阵表示。cQED`PNR`Placing`使用矩阵构建图形，并生成图形的位置坐标。利用来自GDSII文件中引用单元的其他信息，将坐标转换为实例量子比特的位置，便可以生成一个新的GDSII 文件存储布局。

放置好量子比特后，cQED`PNR`Routing`可以使用半波长谐振器在逻辑连接的端口之间布线。给定端口的两个边缘、半波长谐振器的长度以及曲折线路的最大振幅，该模块可通过固定宽度的导线自动连接两个端口。如图7（彩图扫OSID 码可见）所示，沿着最短路径（虚线）的方向可分为两种类型的区域，即两个过渡区域和曲折区域。过渡区域由一个扇区和一个贝塞尔曲线形部分组成，它们将两个边缘对齐，从而使曲折区域对称。布线步骤完成后，线路参数将存在新的GDSII 文件中。

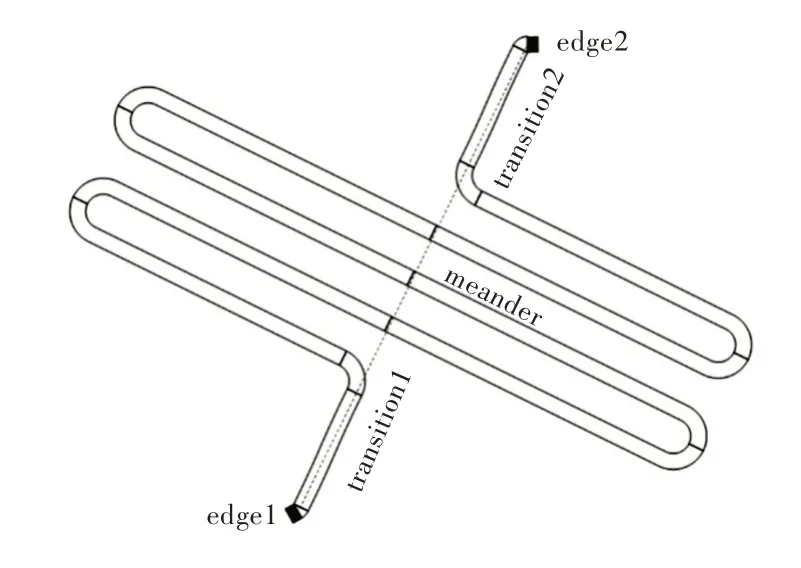
Fig.7 Route to connect two edges（red rectangles）generated by the cQED`PNR`Routing`sub-package图7 cQED`PNR`Routing`程序包生成的连接两个边（红色矩形）的线路

3.7 用户界面模块（cQED`GUI`）

该模块包含多个交互式图形界面工具，可用于快速计算一些问题。参数可以通过GUI 模块输入而不是代码输入，虽然不如使用脚本那么灵活，但特别适合不熟悉编码的用户使用，而且便于演示。从技术上讲，GUI 模块通过在Mathematica 中封装以上6 个模块的功能实现。

4 结语

本文设计了采用Wolfram 语言实现的用于超导量子电子设计的cQED 框架性工具，从单器件分析到布局生成，其功能涵盖单谐振器设计、电路分析、微波工程、布局处理和布线，为了使用方便，还构建了图形交互工具。随着超导量子计算的发展，大规模超导量子比特被集成，量子芯片的设计会变得十分复杂。采用Wolfram 语言实现的cQED易于扩展，可以辅助超导量子电路研究，使超导量子电路的设计自动化，尤其会在大规模超导量子计算电路中发挥重要作用。