磁粉制动器的改进全局快速终端滑模控制

王 惠，白国振，王海波，宋慧文

（上海理工大学 机械工程学院，上海 200093）

0 引言

常见的模拟加载方法有电动伺服加载、机械式加载、电液加载和磁粉制动器加载［1］。由于磁粉制动器具有良好的恒转矩特性和可控性［2-3］，因而在模拟加载领域中得到广泛应用。但由于磁粉制动器存在一定的非线性和滞后性［4］，对加载系统的动态响应和加载精度影响很大。因此，研究加载系统的控制算法对提高系统的加载质量具有十分重要的意义。

针对磁粉制动器的滞后性及非线性，学者提出了多种控制方法：孙毓斌［5］提出了模糊自适应的控制方法；Jing等［6］研究了PID 控制方法在磁粉制动器中的应用；袁宇凤［7］提出引入积分作用的模糊Smith 控制方法，在一定程度上提高了磁粉制动器的加载性能。模糊控制根据系统的实时误差及误差变化率进行模糊推导，得到最佳的控制参数。在进行模糊规则设定时，只需对其数学模型有初步了解即可，因而具有一定的自适应能力，从而提高控制效果，但是在确定模糊规则时需要大量专业人士的相关控制经验［8］；金昊等［9］提出一种模糊单神经元复合智能控制方法，通过单神经元学习算法进行参数自整定，实现单神经元控制器输出增益的实时调节；胡超等［10］、邢华［11］设计了神经网络PID 控制算法，该算法在结构和原理上模拟了人脑中的局部调整和感受野，具有收敛速度快、逼近任意连续函数能力突出的特点，但神经网络的初始权重和阈值对最终的控制效果影响较大，且较难选取。上述几种控制算法虽然在一定程度上不再依赖被控对象的精确数学模型，具有一定的鲁棒性，但其加载的响应速度、加载精度及抗干扰能力等依然需要进一步提高。

本文针对上述算法中存在的问题，从快速性、加载精度、抗干扰能力方面设计一套更适合于磁粉制动器的智能控制算法——基于扰动观测器的磁粉制动器全局快速终端滑模控制算法。该算法对磁粉制动器精确的数学模型依赖度相对较低，能够进一步提高系统的加载精度、抗干扰能力和响应速度。

1 磁粉制动器扭矩加载系统数学模型

1.1 系统基本模型

建立数学模型方法主要分为机理分析法和系统辨识法两种［12］。本文首先通过机理分析法推导出系统的名义模型，然后利用系统辨识法确定名义模型中的未知部分。磁粉制动器扭矩加载系统的典型控制结构如图1 所示。

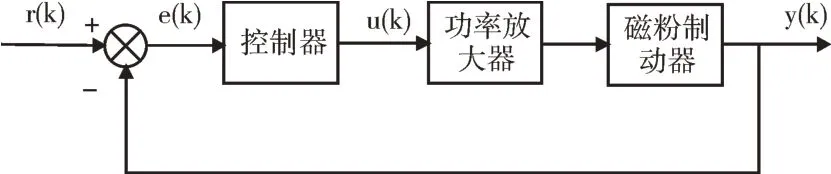
Fig.1 Typical control structure of torque loading system of magnetic powder brake图1 磁粉制动器扭矩加载系统典型控制结构

由图1 可知，磁粉制动器扭矩加载系统由功率放大器和磁粉制动器两部分组成。

1.1.1 功率放大器数学模型

功率放大器把控制器输出电压信号转换成磁粉制动器的输入电流信号，其数学模型如下：

1.1.2 磁粉制动器数学模型

设磁粉制动器内定子的外径为Dm、宽度为Lm，则其输出转矩为：

式（2）中：σ为内定子单位面积上的剪切应力。

依据莫尔—库仑原理［13］有：

式（3）中：σ为气隙磁导率，B为磁粉间的磁感应强度，μδ为磁粉槽内磁粉磁导率。

将式（3）代入式（2）有：

将式（4）线性化并拉式变换得：

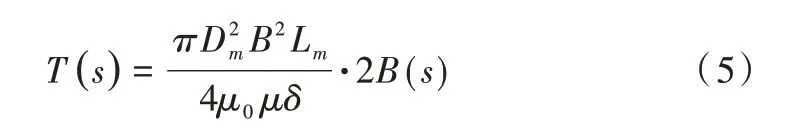
在磁粉制动器磁路中，由磁场欧姆定律得：

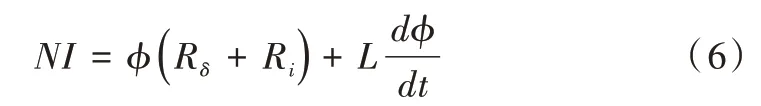
式（6）中：Rδ为隙及磁粉总磁阻，Ri为铁磁阻，L为电感量，N为线圈匝数，I为线圈电流。

不考虑边沿磁通量带来的影响，则穿过粉槽中的磁通量为：

式（7）中：Sδ为磁粉填充区域垂直于磁路的有效面积。

将式（7）代入式（6）得：

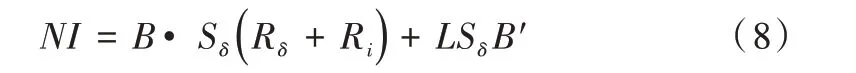
将式（8）拉氏变换得：

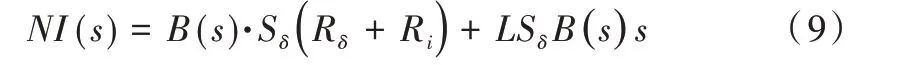
联立式（5）和式（9）得：

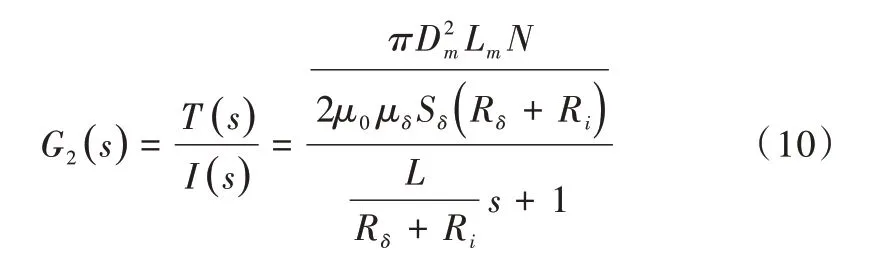
由于磁粉材料存在一定的滞后性，因此在式（10）的基础上串联一个滞后环节，则磁粉制动器的数学模型为：

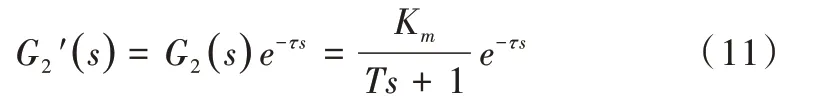
由式（11）可知，磁粉制动器是一阶惯性纯滞后系统，影响其工作性能的参数有增益Km、时间常数T以及滞后时间τ。

结合式（1）和式（11）得到系统的传递函数为：

1.2 系统近似数学模型

经典系统辨识方法中，最小二乘法具有计算量小、原理简单的特点，但其估计有偏差，要求输入信号已知且具有丰富的变化［14-16］。现代系统辨识方法中，粒子群优化算法具有实现容易、精度高、收敛快等特点，其在解决系统辨识问题中具有显著的优越性［17-19］。

针对同一系统模型，分别使用两种方法进行辨识。两种方法采取同样的准则函数进行评判，即二乘模，具体步骤如下：

（1）选定模型传递函数。

（2）在MATLAB 中对模型输入幅值为1 的阶跃信号采样时间设为1s，仿真时间为35s，得到35 组输入输出数据。在输出数据上加入均值为0、方差为0.1 的白噪声作为干扰信号。

（3）采用最小二乘法辨识结果如式（14）所示，辨识曲线如图2 所示，辨识准则函数值J 为8.509 6。

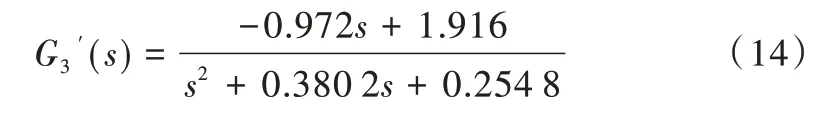
（4）利用粒子群优化算法辨识。辨识参数集为X=［K1 K2 T1 T2］，粒子群规模为80，最大迭代次数为200 次，X中3个参数范围均为［-2，2］，粒子最大速度Vmax设置为1.0，学习因子c1=1.3，c2=1.7，采用线性递减的惯性权重，wmax=0.90，wmin=0.1。辨识结果如式（15）所示，辨识曲线如图3所示，辨识准则函数值J 为2.556 9。

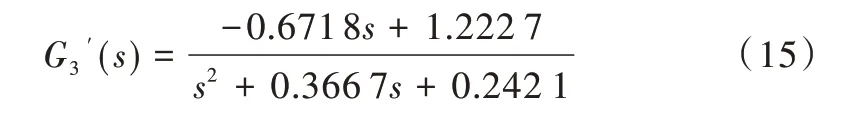
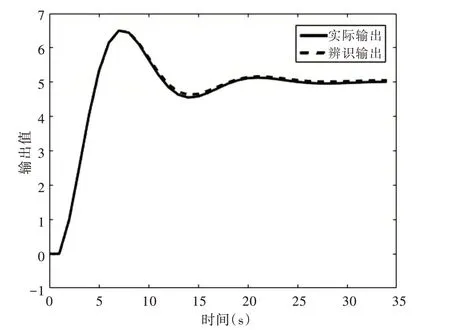
Fig.3 Identification curve of particle swarm optimization algorithm图3 粒子群优化算法辨识曲线

对系统采用上述两种方法进行辨识，对辨识结果进行分析比较，可知粒子群优化算法的辨识效果优于最小二乘法，因此本文采用粒子群优化算法对系统参数进行辨识。

本文加载系统的控制回路为单回路形式，其系统框图如图4 所示。

Fig.4 Diagram of single loop control system图4 单回路控制系统框图

由图4 可知，需要辨识的控制对象传递函数为Gp（s），在不考虑噪声干扰情况下，Y（s）即为该控制对象的输出信号，R（s）为整个控制系统的输入信号，U（s）为控制器的输出信号，也是控制对象的输入信号。本文不考虑控制器传递函数的辨识，只关心控制对象传递函数的辨识，即Gp（s）。因此，输出信号和输入信号分别为Y（s）和U（s）。

本次辨识采用的输入信号为阶跃信号，信号幅值大小为2V，采样时间为1ms，采样次数5 000 次。采样结束后，将从现场采集到的数据保存。将保存的输出数据利用粒子群算法进行辨识，通过机理分析法得到控制对象的基本数学模型，得到待辨识的参数个数为3 个，因此取粒子维数为3。粒子群数量设置为80，最大迭代次数G=200，参数搜索范围为［0，50］，粒子速度范围为［-1，1］，学习因子c1=1.3、c2=1.7，采样线性衰减0.1≤w≤0.9，准则度函数为二次模。利用采集到的数据进行辨识后结果如下：

1.3 辨识结果分析

为保证辨识后系统数学模型的精确度，对粒子群优化算法的辨识结果进行验证。将粒子群算法辨识模型的开环输出值与系统的实际输出值进行比较，结果如图5 所示。

Fig.5 Validation results of identification model图5 辨识模型验证结果

由图5 可知，两个输出值的波形基本吻合，因此可将粒子群优化算法的辨识结果作为被控对象的实际模型进行后续控制算法研究。

在MATLAB 中绘制系统的开环伯德图，如图6 所示，由图6 可知系统的增益裕度和相位裕度均大于0，系统稳定。

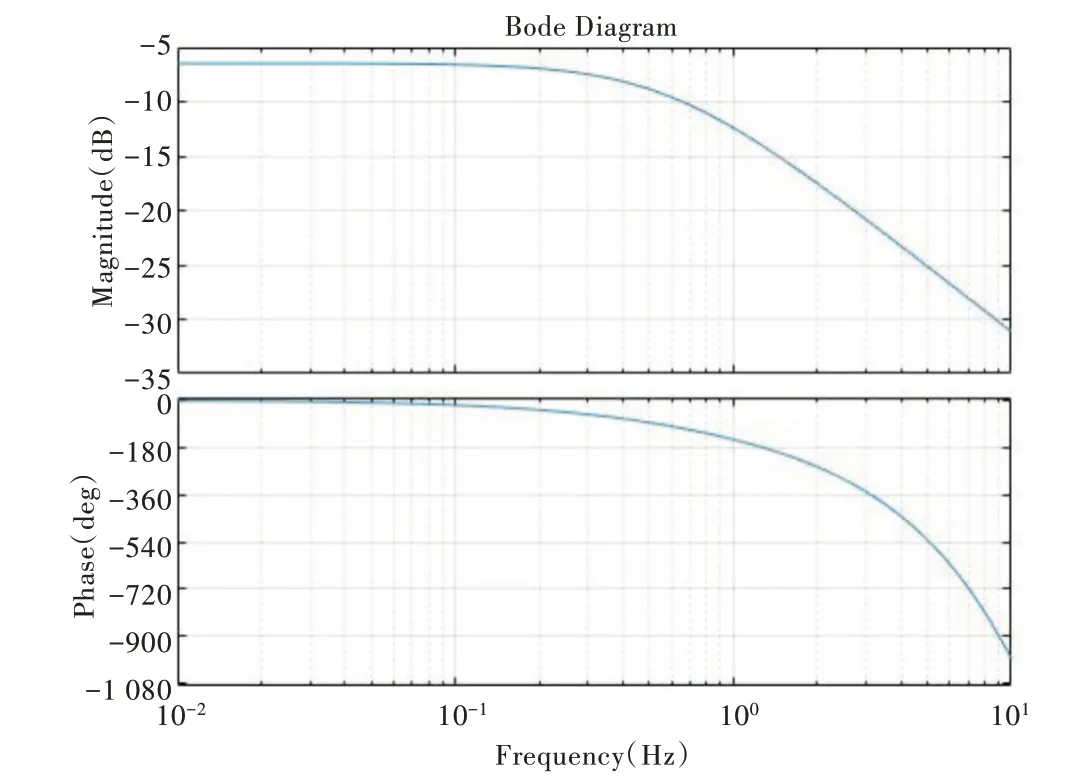
Fig.6 Open loop Bode diagram of the system图6 系统开环伯德图

2 全局快速终端滑模控制器设计

2.1 控制器设计

将磁粉制动器的传递函数转化成状态空间方程：

2.2 滑模运动时间分析

对式（28）两边取对数，即可求得系统到达平衡状态的有限时间为：

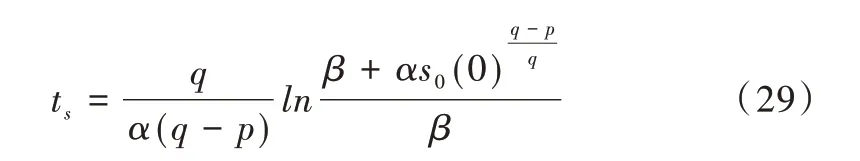
因此，通过设定α、β和q可使系统在有限时间内达到平衡状态。

2.3 稳定性分析

3 基于扰动观测器的磁粉制动器全局快速终端滑模控制器设计

3.1 扰动观测器设计

扰动观测器利用已知名义模型信息，观测实际对象与名义模型的输出差异，即等效干扰，然后将等效补偿引入到控制器一侧，实现对扰动完全抑制，其标准结构如图7 所示。

Fig.7 Basic structure of disturbance observer图7 扰动观测器基本结构

图7 中，Gp（s）为被控对象模型，u为参考控制输入，e为实际控制输入，d为外部干扰，y为系统输出，n为测量噪声，为观测出的等效干扰。由图7 可得等效干扰值为：

式（33）说明，如果观测器可在实际物理系统中实现，则利用上述方法就可实现对扰动的准确观测。但实际构造观测器时存在以下问题：①被控对象的传递函数阶次通常不为零，因此其在物理上无法实现；②被控对象的精确传递函数无法获取；③在实际测量时难免存在测量噪声，会导致测量精度下降。为解决这些问题，在等效干扰后引入低通滤波器Q（s），用名义模型的逆系统代替（s），得到扰动观测器等效框图如图8 所示。

Fig.8 Equivalent block diagram of disturbance observer图8 扰动观测器等效框图

由式（35）可知，滤波器Q（s）对y（s）的影响非常大，Q（s）带宽的设计与扰动观测器的鲁棒性和干扰抑制能力密切相关，Q（s）的设计与系统输出y（s）的关系为：

在低频段，Q（s）=1，扰动观测器可以实现对干扰的完全抑制。在高频段，Q（s）=0，扰动观测器可以完全克服高频测量噪声的影响，但对于模型参数的摄动及外部干扰完全没有抑制作用。因此，本文采用低通滤波器来设计Q（s）。

3.2 低通滤波器Q（s）设计

目前较为流行的低通滤波器设计方法由Lee［20］提出，其表达形式为：

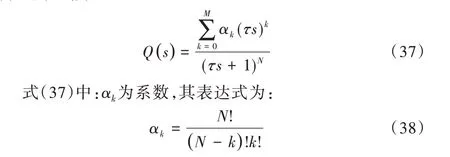
式（38）中：N为分母的阶次，M为分子的阶次，N-M为相对阶次，τ为时间常数。

在全局快速终端滑模基础上引入扰动观测器后，系统控制框图如图9 所示。

Fig.9 System control frame with disturbance observer图9 带扰动观测器的系统控制框图

3.3 抗扰动仿真分析

在MATLAB/simulink 平台进行抗扰动能力仿真，外界干扰信号和指令信号分别为d（t），y（dt）：

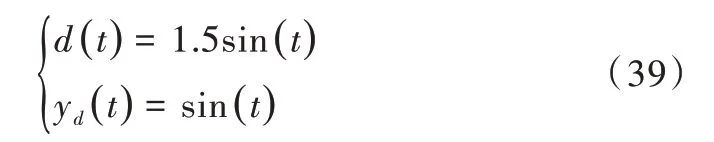
扰动观测器中Q（s）低通滤波器参数设置为：N=3，M=1，k=0.1，τ=0.001；滑模控制部分参数取c=10，ε=0.5，k=10。加入扰动观测器和未加入扰动观测器的全局快速终端滑模控制仿真结果如图10、图11 所示。

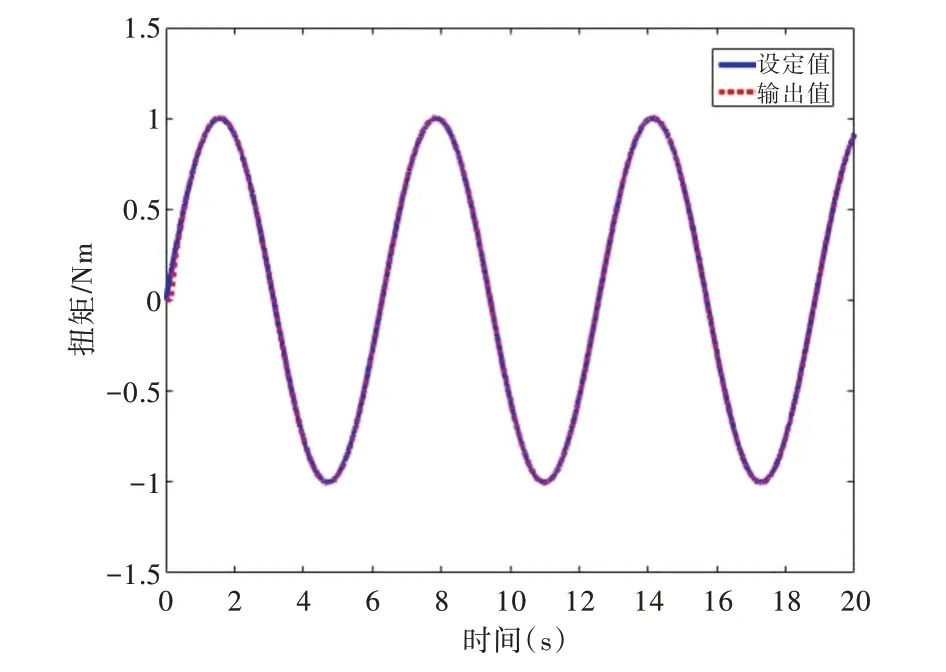
Fig.10 Control effect after adding disturbance observer图10 加入扰动观测器后的控制效果

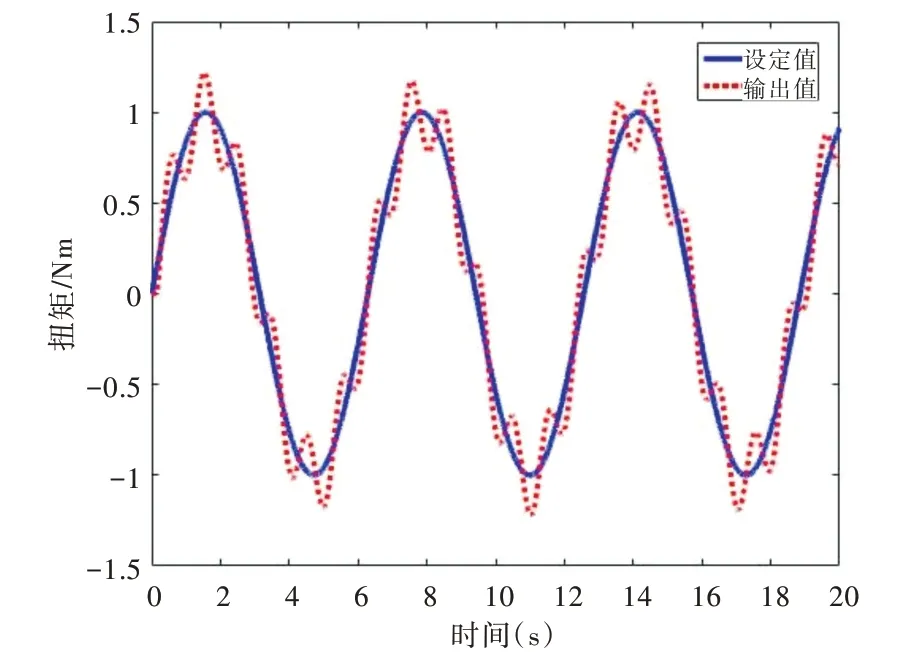
Fig.11 Control effect without disturbance observer图11 未加入扰动观测器的控制效果

4 仿真分析

利用MATLAB/Simulink 平台建立磁粉制动器扭矩加载系统控制仿真模型，采用常规PID 控制、指数趋近律的滑模控制、加入扰动观测器的全局快速终端滑模控制3 种方法，对周期为6s、幅值为1NM 的正弦信号进行跟踪，验证本文提出策略的正确性和可行性。

ε=0.5，k=10；基于扰动观测器的全局快速终端滑模控制（GFTSMC+DOB）系统初始状态为x=［0，0］，α=2，β=1，n=1，m=3，q=5，p=9，γ=10，φ=10，Q（s）低通滤波器的参数设置：N=3，M=1，k=0.1，τ=0.001。3 种控制方法的仿真结果如图12 所示。

Fig.12 Sinusoidal tracking effect of three methods without interference图12 无干扰下3 种方法正弦跟踪效果

在系统模型中加入干扰信号，干扰信号为1.5sin（2πt），输入信号与各控制器的参数如上所述。加入干扰信号后的仿真结果如图13 所示。

由图12 和图13 可知，在无干扰情况下，GFTSMC+DOB和RLSMC 控制比PID 控制的跟踪效果好，GFTSMC+DOB 的跟踪效果最优。在有干扰情况下，GFTSMC+DOB 控制方法效果最优；相比于其他两种控制方法，RLSMC 控制方法对系统的控制性能影响较小；而常规PID 对系统的控制性能影响较大，证明GFTSMC+DOB 控制方法具有较强的抑制干扰能力。

5 结语

本文针对磁粉制动器的非线性和滞后性对加载系统动态响应和加载精度的影响，设计了一种基于扰动观测器的磁粉制动器全局快速终端滑模控制器。通过电磁学原理推导出系统的基本数学模型，并分析比较了最小二乘法与粒子群优化算法对系统辨识的优缺点。采用粒子群优化算法对系统进行辨识，得到系统近似的数学模型。对扰动观测器进行设计，并在MATLAB/Simulink 平台上进行抗扰动能力仿真，完成本文控制算法与PID 控制算法、趋近律滑模控制算法对正弦信号进行有干扰信号和无干扰信号的仿真对比实验。实验结果表明，本文设计的控制算法对系统的不确定性和外部扰动具有较好的鲁棒性，在无干扰情况下，GFTSMC+DOB 的跟踪效果最优，在有干扰情况下，GFTSMC+DOB 控制方法效果最优。后续将对本文提出的控制方法在平台中进行验证。