改进误匹配剔除的SLAM 算法

伞红军，王汪林，陈久朋，王 晨

（昆明理工大学机电工程学院，云南昆明 650500）

0 引言

同步定位与地图构建（Simultaneous Localization and Mapping，SLAM）是移动机器人在未知环境下实现自主定位导航的核心技术［1］。相较于激光、雷达，视觉同步定位与地图构建（Visual SLAM，VSLAM）因采用视觉传感器而具有一定成本优势，成为SLAM 领域的热门研究方向之一［2］。

按照视觉里程计的计算方法不同可将VSLAM 分为直接法［3］和特征点法［4］。直接法基于灰度不变假设直接根据像素亮度信息估计相机位姿，完全不用计算关键点和描述子，但在高光环境中存在退化或失效等现象。Engel 等［5］结合地图梯度与直接法提出LSD-SLAM，其可在CPU 上实时构建半稠密地图，缺点是在快速运动和曝光环境中相机位姿会丢失；Forster 等［6］提出SVO（Semidirect Visual Odome⁃try）算法，使用半直接法利用稀疏特征点定位相机位姿，运行速度快，但跟踪丢失现象严重，且不适用于高光环境；En⁃gel 等［7］提出的DSO（Direct Sparse Odometry）是纯直接法的SLAM 系统，能够快速实现稀疏点云地图的构建，但对光照敏感，鲁棒性不高。

特征点法使用特征点的匹配计算相机位姿，对关键点的提取与匹配精度要求高，如果存在太多误匹配，相机位姿估计会有很大偏差。因此，如何有效剔除误匹配并提高位姿估计精度是SLAM 研究者们一直关注的问题。传统SLAM 系统使用随机抽样一致（Random Sample Consensus，RANSAC）算法［8］剔除误匹配特征点，该算法通过随机抽取样本数据计算模型参数，能快速找到最优估计［9］。Mur-Ar⁃tal 等［10］提出一个基于特征点的实时SLAM 系统ORBSLAM2，无论规模大小、室内室外都可以运行。该系统对剧烈运动也很鲁棒，能实时计算相机轨线，并生成场景的稀疏三维重建，但耗时长且存在一定的误匹配。

本文基于ORB-SLAM2，在关键帧图像匹配的过程中引入一种新的误匹配剔除算法替换RANSAC 算法。其选用kinect v1 深度相机，先对TUM 数据集进行实验，获得相机轨迹，进而验证改进SLAM 算法的可行性。同时，在实验室环境中对改进SLAM 算法进行三维稀疏点云地图构建。结果表明，相较于传统的RANSAC 算法，改进误匹配剔除的SLAM 算法增加了正确匹配点对数量，提高了相机位姿估计精度。

1 特征点匹配算法

在实时性方面，特征点匹配算法ORB（Oriented FAST and Rotated BRIEF）［11］是VSLAM 系统中最具代表性的特征提取算法之一。ORB 改进了FAST（Features from Accelerat⁃ed Segment Test）算法中检测子不具有方向性的问题，采用计算速度极快且具有旋转不变性的二进制描述子（Binary Robust Independent Elementary Feature，BRIEF）［12］，使图像特征提取速度大大加快。

1.1 FAST 特征点检测

FAST 是一种高效的特征点（角点）检测算法，可基本满足实时检测需求，是计算机视觉领域最主流的角点检测算法之一。FAST 检测角点的基本思路如图1 所示，以某一像素点为圆心，半径值固定的圆周上其余像素点与圆心像素点灰度值差别较大即可被认为是角点。由于只需要比较一维灰度值的大小，该算法计算时间大大缩短。对于灰度图像，FAST 算子考察的属性是像素与其邻域的灰度差异，检测过程如下：

（1）在图像中选取一像素点p，即可确定出以p 点为圆心、半径为3 的16 个像素点，将其灰度值与p 点进行比较。若有连续的n（通常取12）个像素点比p 点灰度值大或者小，则p 点即为特征点。为提高检测效率，通常可检测图1中1、5、9、13 四个位置中是否有连续3 个及以上像素点大于或小于p 点的灰度值，若满足则需进一步比较，若不满足可直接排除。

Fig.1 FAST feature points图1 FAST 特征点

（2）筛选最优特征点。

（3）去除局部较密集特征点，删除p 点与周围特征点偏差绝对值之和较小的特征点。

（4）实现特征点的多尺度不变性。通过构建图像金字塔，在金字塔的每一层检测角点，实现尺度不变性，特征的旋转通过灰度质心实现［13］。设置比例因子和金字塔层数，对原图像进行不同层次的降采样，将不同比例图像中提取的特征点总和作为FAST 特征点。

1.2 BRIEF 特征描述子

BRIEF 是一种二进制描述子，即每个关键点是由0 和1组成的二进制字符串。定义S×S 大小的图像领域P 的二值化τ 为：

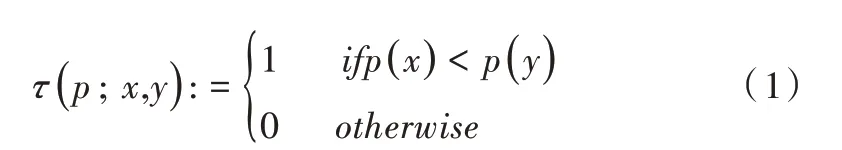
式中，p（x）为图像邻域P 在点x 的灰度值。

那么，nd个测试点对比形成描述子的计算公式为：

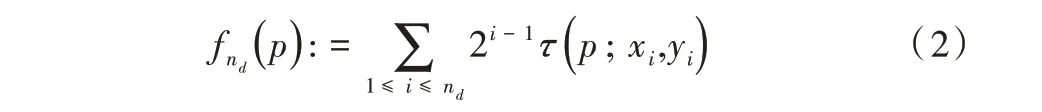
式中，nd可为128、256 或512 等。

上述描述子不具有旋转不变性，ORB 算法利用角点方向使描述子包含方向信息。

1.3 特征点匹配

在完成特征点提取与描述子计算后，还需对图像中的特征点进行匹配计算以精确判断两幅图像之间的相似性。特征匹配主要分为暴力匹配法（Brute Force，BF）和快速最邻近搜索库法（Fast Library for Approximate Nearest Neigh⁃bors，FLANN）。BF 即采用图像特征点暴力匹配找到点集一中每个descriptor 在点集二中距离最近的descriptor；而FLANN 一般将点集一作为训练集对应模板图像，点集二作为查询集，对应查找模板图的目标图像，通过直接计算两个特征点之间的汉明距离［14］是否大于参考值以判别图像相似性。

2 基于ORB-SLAM2 系统框架的改进误匹配剔除算法

2.1 粗匹配

通过对ORB 特征点进行粗匹配排序相关函数，根据排序结果构造一个假设的生成集并随机采样，以获得描述与该匹配点集相对应的图像变换信息的最佳拟合模型。

将含有N 个点的数据集表示为μN，按照相关性q 对μN中的两个采样点ui、uj进行降序排列，表示为：

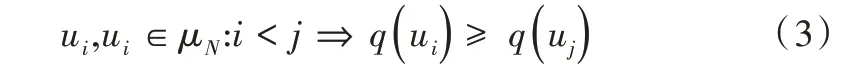
然后从μN数据集中抽取大小为m 的TN个样本作为采样点集合M，表示为的评价函数：

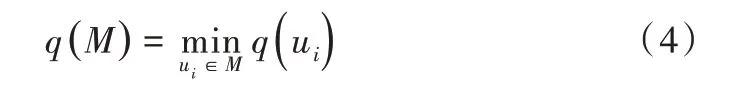
在采样数据集中提出假设，即内部点比外部点更多，具体算法为：

（1）输入一个包含误匹配对的粗匹配点对集M，并根据相关性函数对M 中的匹配点进行排序。在排序结果中，从大到小选取m 个数据子集Sm构建初始拟合模型。

（2）将粗匹配点对集合M 中的数据点代入初始拟合模型，根据生成集大小之间的相关性计算误差，测试模型性能，并保留评估值较高的ORB 特征点集合。

（3）当迭代次数达到设置的阈值时，获得描述与匹配点集相对应的图像变换信息的最佳拟合模型［15］。

2.2 运动估计

对相邻两帧RGB-D 图像进行特征点提取与匹配，获得多对匹配的3D 点：

求解最优的R、t，使得：

根据上式可以看出，两组3D 点的变换可采用迭代最近点算法（Iterative Closest Point，ICP）求解，分为两种方式，分别为利用线性代数求解，如奇异值分解（Singular Value De⁃composition，SVD），以及非线性优化方式求解。

首先定义第i 对点的误差项为：

然后构建最小二乘问题求解R、t：

两组点的质心可定义为：

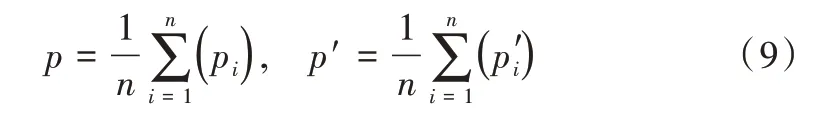
目标函数可简化为：

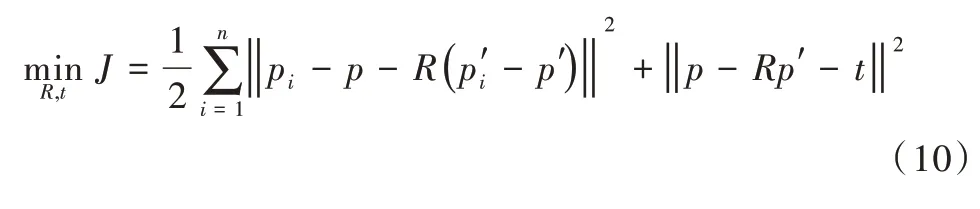
由上式可看出，采用SVD 法求解ICP 主要分为3 个步骤：

（1）计算匹配点的质心位置p、p'，计算去质心坐标。

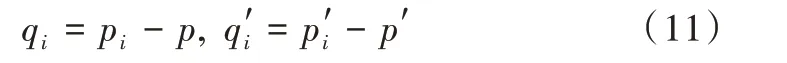
（2）计算旋转矩阵R*。

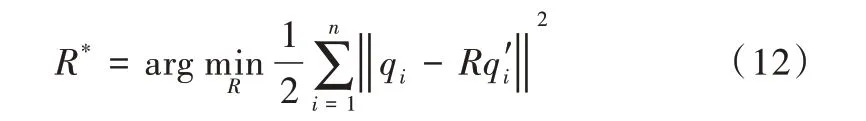
（3）计算平移量t*。

只要求出特征点对之间的旋转量R，平移量t 便可通过简单计算得到。展开关于R 的误差项，表示为：

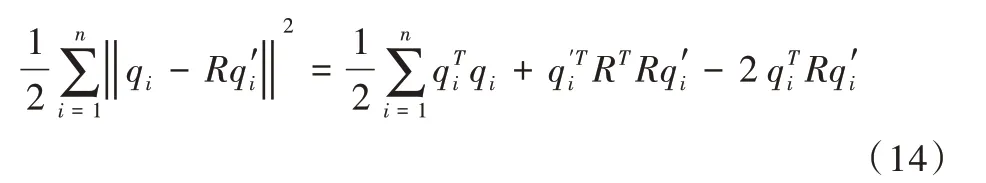
展开项中，第一项与R 无关，第二项中RT R=I。因此，目标函数优化为：

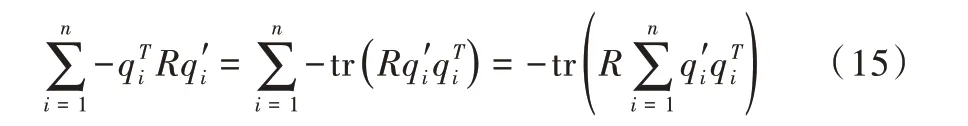
通过SVD 法求解出最优R，定义矩阵：

式中，W 为3×3 矩阵，对W 进行SVD 分解，得出：

式中，U、V 均为对角阵，∑为奇异值组成的对角阵，其中元素从大到小排列。当W 满秩时，R 为：

求解R 后，代入式t*=p-Rp'可求解出平移量t。当R的行列式为负值时，则取-R 为最优解。

3 SLAM 系统总体实现与实验

3.1 ORB 特征点直接匹配、RANSAC 算法与改进误匹配剔除算法实验对比

实验环境为Ubuntu18.04 系统、Intel i7-8750H CPU、NVIDIA GTX1060 GPU、8GB 显存，采用OpenCV3.2.0 开源库。采集像素大小为640×480 的真实环境图像进行实验，对比ORB 特征点直接匹配、RANSAC 算法和改进误匹配剔除算法的匹配效果。实验结果如图2 所示，图中的原点代表图像之间匹配的特征点，原点之间的直线代表特征点的对应匹配关系。

Fig.2 Comparison of mismatch elimination of three algorithms图2 3 种算法误匹配剔除对比

从图2（a）中可以看出，ORB 特征点直接匹配会因各种原因造成错误匹配；图2（b）的RANSAC 算法虽然在一定程度上降低了错误匹配数量，但匹配点数偏少；图2（c）的改进误匹配剔除算法匹配点数适中。3 种算法的误匹配剔除时间与匹配点对数如表1 所示，其中改进误匹配剔除算法的运行速度比RANSAC 算法提升了38%，匹配点对数量提高了7%，符合SLAM 系统实时性与匹配准确性的要求。

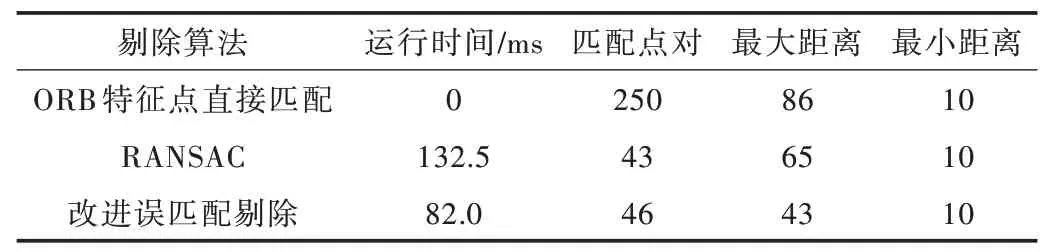
Table 1 Experimental data of mismatched feature points eliminated by the three algorithms表1 3 种算法剔除误匹配特征点实验数据

3.2 基于数据集的SLAM 算法仿真

在仿真环境下，采用德国慕尼黑工业大学的TUM 公开数据集［16］验证基于改进误匹配剔除的SLAM 算法的有效性。该数据集中包含各类环境序列，且采用专业设备采集真实运动轨迹和绝对位姿，因此“3.1”项下选取fr1_desk 这个具有丰富纹理的办公环境图像序列对比算法的匹配效果。通过EVO 工具库分别绘制SLAM 计算出的位姿与数据集提供的真实位姿，采用绝对轨迹误差（Abosulte Trajectory Error，ATE）和均方根误差（Root Mean Square Error，RMSE）等量化指标［17］评价ORB SLAM2 算法与基于改进误匹配剔除的SLAM 算法的优劣性，实验结果如图3、图4 所示。从三维轨迹图可以看出，基于改进误匹配剔除的SLAM 算法的估计轨迹比与ORB SLAM2 算法更连贯，更接近于真实轨迹。

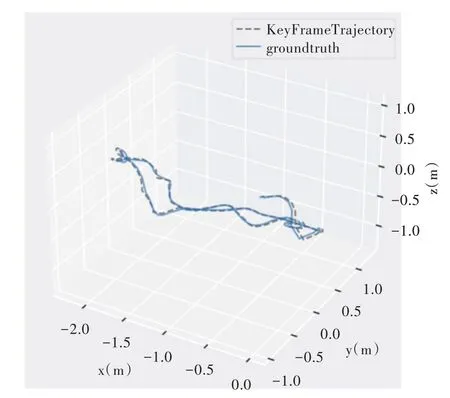
Fig.3 ORB SLAM2 trajectory图3 ORB SLAM2 轨迹

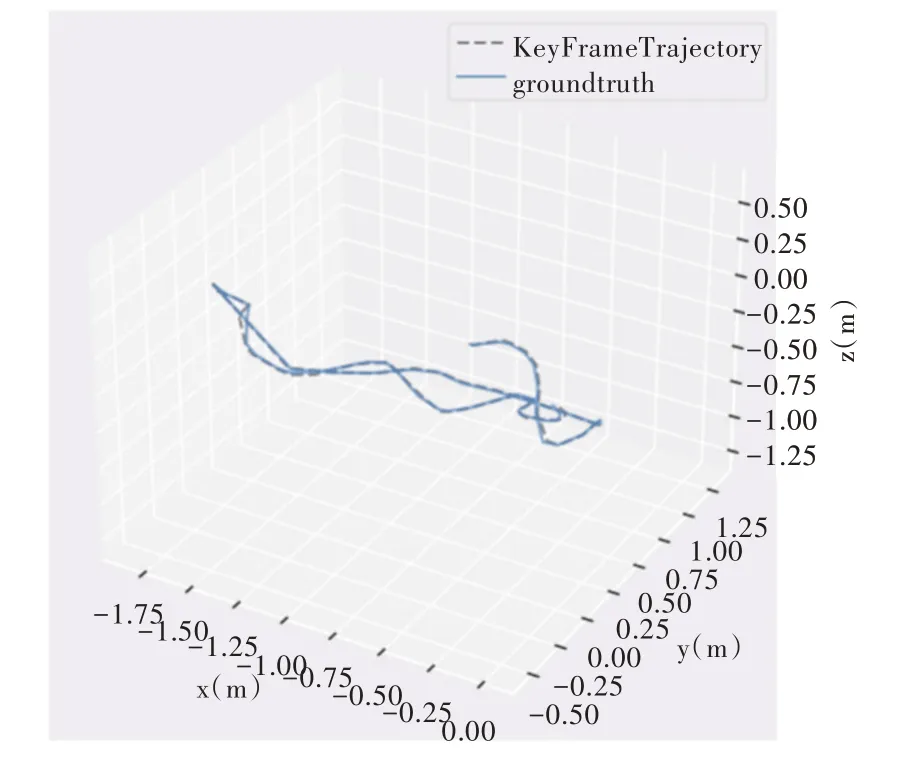
Fig.4 SLAM algorithm based on improved mismatch elimination trajectory图4 基于改进误匹配剔除的SLAM 算法轨迹

绝对位姿误差APE 指SLAM 系统估计位姿与真实位姿的直接差值，可直观反映算法精度与轨迹全局一致性。对于运动估计轨迹序列，真实轨迹序列定义为：

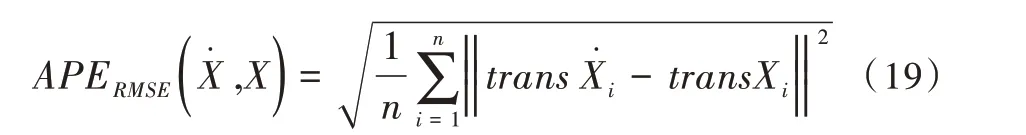
式中，trans 表示姿态的平移向量。

根据位姿时间戳将真实值与估计值对齐，计算对齐后的APE，绘制其折线图和数值分布轨迹图，具体如图5 所示。详细比较误差值APE 的最大值Max、平均数Mean、最小值Min 和RMSE，如表2 所示。实验数据表明，基于改进误匹配剔除的SLAM 算法的RMSE 比改进前的ORB SLAM2优化了26%，均值优化了20%，最大值与最小值也进一步说明了改进算法的可靠性。图6（彩图扫OSID 码可见）直观地采用颜色深浅描述两种算法的误差，蓝色越深代表误差越小，红色越深代表误差越大。显然，ORB SLAM2 的偏红色区域多于基于改进误匹配剔除的SLAM 算法，说明后者绝对轨迹误差较小。

Fig.5 APE line chart of the two algorithms图5 两种算法的APE 折线图

Table 2 APE experiment results表2 绝对位姿误差实验结果 单位：m

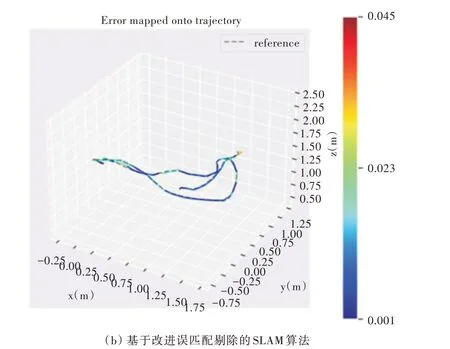
Fig.6 APE map of the two algorithms图6 两种算法的APE map 图

3.3 实际场景实验

实验环境为室内办公桌，工控机配置为Ubuntu18.04 系统，Intel i7-8750H CPU，NVIDIA GTX1060 GPU，8GB 显存，视觉传感器为kinect v1 深度相机，连续采集图像序列进行实时计算。从实验结果来看，基于改进误匹配剔除的SLAM 算法能实时运行，跟踪稳定，无丢帧和失帧现象，能建立三维稀疏点云地图，具有一定可行性，具体如图7 所示。

Fig.7 Keyframe trajectory and 3D sparse point cloud map图7 关键帧轨迹与三维稀疏点云地图

4 结语

本文提出一种基于改进误匹配剔除的SLAM 算法，并对其实时性、鲁棒性、位姿估计精度和建图性能进行了测试。实验结果表明，该算法在特征检测匹配和去除误匹配环节不仅能保留更多正确匹配点，运行速度也有所提高。相较于ORB-SLAM2，基于改进误匹配剔除的SLAM 算法获得的真实轨迹与计算轨迹重合度更高，均方根误差也更小，具有一定可行性。然而，该算法未充分利用图像中的语义信息，未来可考虑将环境中的语义信息加入SLAM 算法中，帮助智能移动机器人更精确地获取自身位姿，实现在未知环境中的导航与路径规划。