基于PSO-SVM 的产品服务系统配置
2021-08-24崔兆亿耿秀丽
崔兆亿,耿秀丽
(上海理工大学 管理学院,上海 200093)
0 引言
服务型制造是《中国制造2025》九项战略任务和重点之一,是我国经济实现“创新驱动、转型升级”的重要途径。制造业和服务业的融合改变了制造业产业形态,引发了制造模式改革。企业为客户创造最大价值,提供产品和服务结合的整体解决方案,即产品服务系统(Product Service System,PSS)。PSS 的重要特征是满足客户个性化需求和配置。PSS 方案配置强调根据客户需求快速准确地设计出合适的模块实例组合。
现有PSS 配置方法主要有遗传算法、神经网络和多目标规划等方法。Sheng 等[1]在模块划分的基础上,提出基于遗传算法的PSS 方案配置优化方法,而该方法需要设置权重,涉及个人经验和偏好等因素,缺乏客观性;Wei 等[2]提出一种基于多目标遗传优化算法与模糊选择机制的方法,以解决多目标优化配置问题;Xuanyuan 等[3]提出基于多目标优化方法进行产品配置,并使用多目标遗传算法从可行解中找到Pareto 最优解集,能够很好地解决多目标优化问题,但维度较大时容易出现早熟;Shen 等[4]集成局部集群神经网络与Rulex 算法,以提取服务参数、功能需求、客户特征或产品特征之间的配置规则,从而提升配置解决方案有效性。但是,神经网络遵循基于训练集误差的经验最小化风险方法。因此,它不能保证所得模型具有良好的泛化性能。
PSS 配置目标是为客户的不同需求提供差异化PSS 配置方案,即从产品模块与服务模块的实例中找出特定需求的实例组合进行分类。基于统计学习理论的支持向量机(Support Vector Machines,SVM)能够很好地解决分类问题。它以解决小样本量和非线性问题而著称,并且比传统学习算法表现更好[5]。SVM 方法已成功应用于模式分类和回归领域。本文利用SVM 方法良好的分类能力,将特定的客户需求作为模型输入,输出个性化PSS 配置方案。
SVM 虽然有许多优点,但是在处理大样本容量等分类问题时存在不足。当训练样本数为N时,支持向量机时间复杂度接近N2。另外,SVM 在选取参数时具有高度依赖性,对核函数的选取和惩罚因子的设定要求极高。于是很多学者利用遗传算法和网格搜索等算法对SVM 参数进行优化改进。Huang 等[6]提出GA-SVM 模型分析气候变化和人类活动对植被覆盖变化的定量贡献,使用遗传算法对SVM 中的损失参数、核函数参数和损失函数epsilon 值进行优化;Chen 等[7]提出一种基于GA-SVM 的拉曼光谱技术,用于快速有效地筛选人乳头瘤病毒,并通过使用遗传算法优化SVM 模型中的惩罚因子和核功能参数提高模型准确性;Huang 等[8]利用遗传算法对SVM 参数进行优化,并基于精确率和权重惩罚因子提出一种新的适应值评估函数,尽管遗传算法可以提高SVM 模型准确性,但它容易出现过早收敛的问题;Phan 等[9]在遗传算法基础上对SVM 模型训练样本特征进行了加权,算法分类效果虽然得到显著提升,但加权大幅增加了参数个数,当样本数量增大时,优化效果随之减弱;Friedrichs 等[10]提出利用固定步长进行网格搜索,寻找合适的SVM 参数,但这仅适用于参数较少的情况,而且实际运用过程中存在计算复杂、耗时长等问题。
粒子群优化算法(Particle Swarm Optimization,PSO)是一种基于群智能的随机优化算法,它从随机解出发,通过迭代寻找最优解,并用适应度评价解的品质。PSO 因具有操作简单、通用性强等特点,引起众多学者注意。Liu 等[11]利用PSO 算法优化SVM 模型参数,以预测每日PM2.5 水平预报,首先通过余弦相似度从6 个常见的气象参数(大气压、相对湿度、气温、风速、风向、累积降水)中提取3 个最相关的参数,以提供SVM 模型所需的气象模式,然后由相对湿度,风速和风向组成的选定模式获得更高的预测精度;陈晋音等[12]利用粒子群算法的全局寻优能力,通过粒子随机游走进行最优参数搜索,将结果代入SVM 进行样本训练,并与网格算法等进行比较,验证了PSO-SVM 准确率更高;García 等[13]提出一种混合PSO 优化的SVM 模型以预测螺旋藻生长周期,利用3 种不同的核(线性、二次和RBF)进行回归,并分别获得0.94、0.97 和0.99 的测定系数,最后通过PSO-SVM 模型对实验数据(Chl-a 浓度)进行拟合,并证实了该模型的良好性能;文献[14-15]利用粒子群算法优化SVM 参数,最终在测试模型中得出了更佳的准确度,验证了该方法的有效性。
本文基于粒子群算法优化支持向量机解决PSS 配置问题。在解决PSS 配置问题中,从产品模块和服务模块的实例中找出特定需求的实例组合进行分类,由此可将PSS 配置问题视为多分类问题,而支持向量机算法能够很好地解决多分类问题。在支持向量机算法基础上,再利用粒子群算法的全局优化能力提高支持向量机模型预测准确性,从而更加准确有效地解决PSS 多分类配置问题。
1 研究框架
PSS 配置设计基于模块化设计思想,即需满足模块化设计基本原则,如模块间功能独立和模块内部独立等。根据模块划分原则确定产品模块和服务模块后,生成多个模块实例,以满足客户的不同需求。根据历史数据利用支持向量机算法得到PSS 配置模型,再利用配置模型预测适合新客户需求的PSS 配置方案。本文提出利用粒子群算法优化支持向量机参数,利用PSO-SVM 模型进行PSS 配置,研究框架如图1 所示。
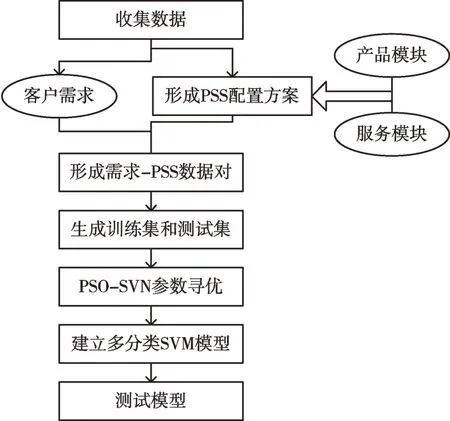
Fig.1 Research framework图1 研究框架
(1)划分产品模块和服务模块后,将客户管理系统中的客户需求及其PSS 配置方案作为训练集和测试集,其中客户需求作为模型输入,满足客户需求的PSS 配置方案作为输出。
(2)设置粒子群算法相应参数,通过粒子群算法优化支持向量机中的核函数б和惩罚因子参数C,然后将求出的最优参数输入到SVM 模型中,利用测试集验证模型准确性。
(3)最后根据设定的模型预测满足新客户需求的PSS配置。
2 基于粒子群算法的支持向量机优化
2.1 支持向量机
支持向量机最初由Cortes 等[14]于1995 年提出,它是基于结构风险最小化原理的监督学习算法。支持向量机基本思想是在样本空间中构造一个超平面作为决策线,将两类不同的样本彼此划分开。与大多数机器学习算法一样,支持向量机也有训练集和测试集,在训练阶段中,给模型提供一系列相关输入和目标输出值的示例;在训练阶段结束后,利用测试集评估学习模型有效性。
SVM 既可以解决二分类问题,也可以解决多分类问题,本文将PSS 配置看作多分类问题。在SVM 解决多分类问题时,将问题分解为多个二分类问题,本文使用一对一(One Versus One,OVO)方法。OVO 方法针对K类问题构造了所有K(K-1)/2 个可能的SVM 分类器,其中每个分类器均由从K类中选出的任意两个类别的训练样本构建而成。构造K(K-1)/2 个分类器后,样本类别可通过投票策略确定,即每个分类器均运行该样本一次,每次分类投一次票,最后将样本分配给票数最多的类别。SVM 具体运算过程如下:
首先,在一个二分类问题过程中,给定一个N个训练样本的集合S,S={(xi,y)i,i=1,2,…,N},其分类超平面表达式为:

其中,w为超平面法向量,b为超平面平移距离。如果所有训练样本均满足约束条件,则说明集合S是线性可分的。

为了增加SVM 分类器对误差的容错性,需要在目标函数中添加松弛变量ξi和一个参数C,所以目标函数可表示为:
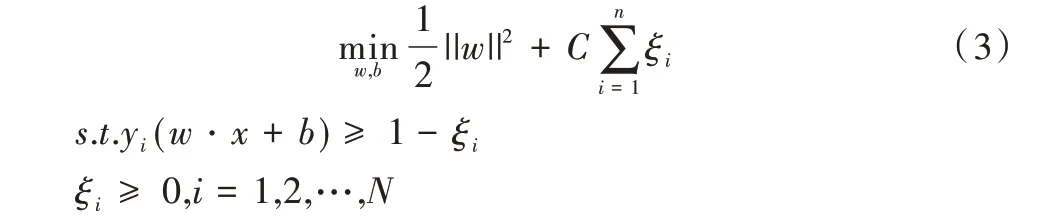
其中C为惩罚参数,用于控制边距最大化与误差最小化之间的平衡。
当面对非线性分类问题时,支持向量机算法需将输入数据映射到更高维的特征空间中解决非线性分类问题。为了避免维数过高的问题,引入核函数k(xi,x)j,本文选用高斯径向基核函数。
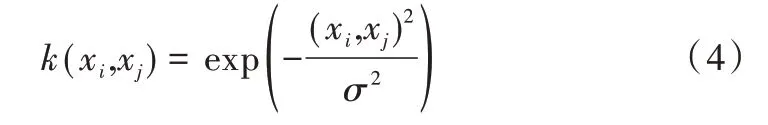
其中,参数σ影响从样本空间到特征空间的映射。将目标函数引进广义拉格朗日乘子,此时,优化问题可以重新表示为:
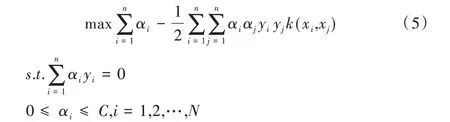
其中,αi为拉格朗日系数,则最终优化的超平面可表示为:

2.2 粒子群优化算法
粒子群优化算法由Kennedy 等[15]在1995 年提出,它是通过模拟鸟群觅食行为衍生而来的一种基于群智能的随机搜索算法。其基本思想是首先一群随机粒子组成种群,然后通过已设定的信息改变粒子位置,以迭代的方式逐步进行优化搜索,最终求出最优解。
粒子群优化算法的数学描述为:在一个n维搜索空间中,设粒子群规模为m,则第i个粒子在n维空间中的位置表示为:
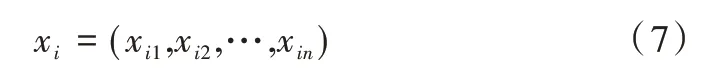
第i个粒子在n维空间中的速度表示为:

第i个粒子当前最优位置为:

整个粒子群当前最优位置为:
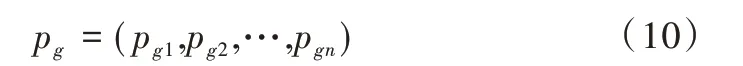
在每一次迭代过程中,粒子群中每个粒子速度更新公式为:
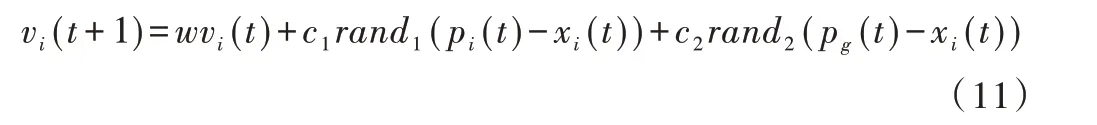
其中c1、c2为学习因子,通常情况下c1=c2=2;w为惯性因子,w值越大,说明全局寻优能力越强,局部寻优能力越弱;rand1、rand2是均匀分布在[0,1]区间的随机数;t代表迭代次数。
粒子群中每个粒子位置更新公式为:
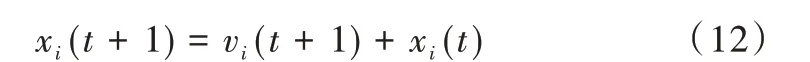
2.3 粒子群算法优化支持向量机的参数
选取不同的核函数将生成不同的支持向量机,从而对PSS 配置产生很大影响。本文选取的是RBF 核函数,因为核函数处理多分类问题时较其它核函数有更高的精度和更快的速度。同时,惩罚因子C对支持向量机模型的准确度影响也很大,所以优化惩罚因子C和RBF 核函数б两个参数是非常重要的。本文采用粒子群优化算法对支持向量机分类器的C、б进行优化。
基于PSO优化SVM参数的过程如图2所示,PSO优化SVM 的具体步骤如下:
(1)导入数据。首先导入训练数据,然后提取训练数据特征值和目标值。
(2)PSO 参数初始化。设定学习因子c1和c2、惯性因子w、最大迭代次数Tmax、当前迭代次数t、初始种群X(t)、粒子初始速度V(t)、粒子维度d。
(3)计算适应值。粒子适应度值越大,说明粒子当前位置越好。本文设置的适应度函数为粒子在5-fold CV 下的分类精度。对于每个粒子而言,将其当前位置适应值与历史最佳位置(pbest)适应值进行比较,如果当前位置适应值更高,则用当前位置更新历史最佳位置。同样对于每个粒子而言,将其当前位置适应值与全局最佳位置(gbest)适应值进行比较,如果当前位置适应值更高,则更新当前位置为全局最佳位置。
(4)更新粒子位置和速度。根据式(11)、式(12)更新每个粒子速度和位置,产生新一代种群。
(5)判断结束条件。当寻优达到最大迭代次数时,寻优结束;否则转至步骤(3),继续寻优。
(6)将得到的粒子最优位置,即最优参数(C,б)赋给SVM。
(7)最后使用测试样本进行测试。
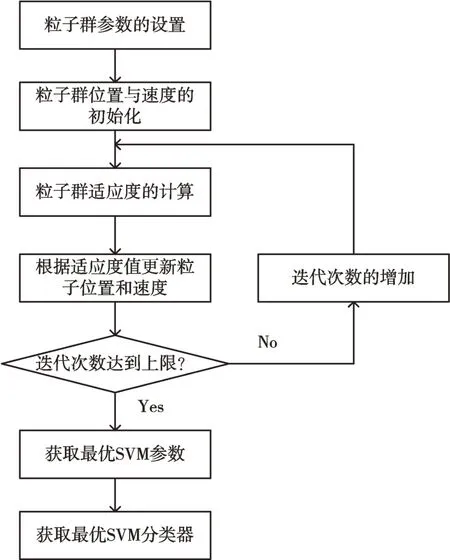
Fig.2 PSO-SVM optimization process图2 PSO-SVM 寻优流程
3 基于PSO-SVM 的PSS 配置方法
根据上文提到的支持向量机算法和粒子群算法,本文将两种算法相结合,提出一种基于PSO-SVM 的PSS 配置方法。实现过程包括两个部分:数据收集及编码与用于PSS配置多分类PSO-SVM 模型构建。
3.1 数据收集及编码
在现实生活中,客户PSS 配置需求是不同的,所以必须收集客户需求特性。以中央空调为例,客户通常使用稳定性强、适应性强等描述PSS 配置。
本文采用PSO-SVM 模型将客户需求转化为特定的PSS 配置方案,当一个新客户提供需求时,将新客户需求特性作为PSO-SVM 模型输入。然后,将其与特定需求有关的PSS 作为经过训练后的PSO-SVM 模型输出显示,以此为PSS 配置指导和建议。数据收集和数据编码是PSO-SVM模型构建中非常重要的阶段。本文将客户需求作为输入,将PSS 配置作为输出。
3.1.1 输入
为使用PSO-SVM 模型,必须将输入表示为实数向量。每个客户需求特征由En={CRi}(i=1,2,…,n)表示,每一个需求特征CRi都有t个可选值。然后通过客户对PSS 需求进行编码,将其作为输入。
3.1.2 输出
在产品和服务领域,将不同的产品组件和服务模块结合构成一个PSS 提供给客户,这些PSS 也称为配置解决方案。它们可以通过产品和服务表示。对于产品模块而言,产品特征可以用PMs表示,PMs={pi|1 3.2.1 多分类SVM 模型构建及最优参数确定 由于PSS 配置问题是一个多分类问题,所以本文首先将其划分为一系列的二分类问题;然后,通过OVO 方法构造所有的二元SVM 分类器,当输入一个样本时,所有分类器都将运行一次;最后通过投票,票数最多的为该样本对应类别。 在运行多类SVM 模型时,为了更好提高模型分类精度,必须确定高斯核函数参数б与惩罚因子C。只有确定参数C与参数б的最佳组合,才能使精度达到最高。本文利用粒子群方法进行k-fold 交叉验证(CV),求出这两个参数最佳组合。对于k-fold 交叉验证,首先将整个训练集分为近似相等样本的k个子集,然后将每个子集当作测试集,其余k-1 个子集当作训练集,以此用作多分类SVM 模型构建条件。因此,每个子集不仅充当了训练集,也充当了测试集。本文使用5-fold 交叉验证进行分析,通过粒子群算法,求出最优参数组合。 3.2.2 模型测试 将具有最佳参数对(C,б)的多分类SVM 模型称为训练模型,再利用已训练好的模型对测试样本进行测试,评估模型性能。本文利用预测正确的PSS 配置数量与PSS 配置总数之比评估训练模型性能。 某公司A 是一家中央空调制造商,为了增强公司竞争力,满足客户个性化、多样化需求,决定向服务型企业转型,为客户提供产品和服务组合的配置方案。该公司提供具有不同特征的产品模块和服务模块,通过融合二者形成产品服务系统方案作为客户配置方案。为了快速响应客户需求,将新客户需求作为SVM 模型输入,通过SVM 模型预测新客户需求对应的PSS 配置方案。 首先从A 公司客户管理系统中的客户需求及其PSS 配置方案中抽取52 个数据样本,用于构建多分类PSO-SVM模型。将这52 个样本分成训练集和测试集,其中训练集样本个数为40 个,测试集样本个数为12 个。将客户需求作为PSO-SVM 模型输入,将为客户提供的PSS 配置方案作为输出。 在客户需求中,一共列举8 个属性,具体如表1 所示。其中[VL,L,ML,M,MH,H,VH]分别表示[非常低,低,较低,中等,较高,高,非常高],其对应编码为[-3,-2,-1,0,1,2,3],本文用[-3,3]区间形式代替。例如某客户需求为环保性高,则可用编码“2”表示。 Table 1 Description of customer requirements表1 客户需求描述 为了对PSS 进行编码,首先需确定产品模块和服务模块。通过查找相关资料,确定中央空调9 个产品组件,每个组件都有一个或多个实例,如表2 所示。在服务模块中,一共有5 个模块,每个模块有多个实例,如表3 所示。 Table 2 Description of product modules表2 产品模块描述 Table 3 Description of service modules表3 服务模块描述 不同的产品组件和服务模块组成不同的PSS 配置方案。由于客户需求各异,本文最终确定6 个PSS 配置方案以满足不同客户的需求。例如,PSS 配置方案“1”可表示为:{A3,B2,C2,D2,E,F1,F3,G,H2,I1,J2,K1,L1,M1,N1};PSS配置方案“2”可表示为:{A2,B1,C2,D1,E,F2,F4,G,H2,I2,J3,K2,L1,M3,N2}。 首先,将52 个样本需求及对应的PSS 配置用于构建PSO-SVM 模型,如表4 所示。 Table 4 Input and output of PSO-SVM model表4 PSO-SVM 模型输入和输出 然后,通过OVO 方法构造多类PSO-SVM 模型。对于由OVO 方法创建的每个可能的二进制PSO-SVM,将高斯RBF 函数选择为内核函数。 下一步结合粒子群优化算法进行5 折CV 的参数寻优,找出最优参数对(C,σ)以运行多类PSO-SVM 模型。在参数寻优过程中,将随机选择的40 个样本用于训练多类PSO-SVM 模型。在粒子群优化算法中,通过每一次迭代得出一个参数对(C,σ),反复迭代到最大的迭代次数,输出最优的参数对(C,σ)。粒子群优化算法具体参数设置如表5所示。 Table 5 Parameter setting of particle swarm optimization表5 粒子群算法参数设定 通过粒子群算法参数值的设定计算出最优的参数对(C,σ),然后将其作为多分类SVM 模型参数设定值进行预测分析。整个过程由Python3.7 及相应第三方库(例如Numpy,Matplotlib,Sklearn 等)完成。 为了评估训练模型性能,使用分类精度作为度量。首先利用粒子群优化算法进行迭代,得出5-fold CV 下的分类精度,其过程如图3 所示。 Fig.3 PSO-SVM parameter optimization图3 PSO-SVM 参数寻优 通过粒子群优化算法得出,当迭代次数到95 次时,5-fold CV 下的分类精度(即89.84%)达到最高,此时得出最优参数值C=15.192 2,σ=0.226 4。将最优参数代入多分类SVM 模型中,并将12 个用于测试集的样本输入模型中测试模型分类精度,测试结果如图4 所示。 Fig.4 Model performance图4 模型性能 从图4 可看出,只有一个最初归类为“2”的样本被误归类为“4”,模型分类精度为91.67%。 为了验证该模型解决实际问题的可靠性,本文对两个新客户需求PSS 配置与实际的吻合性进行测试。第一个新客户需要为医院配置中央空调,其需求是能够除菌、噪声低(即环保性非常高),考虑到病人需求,所以舒适性要求非常高。其输入为{3,3,2,1,-2,3,2,0},输出的结果为配置方案“6”,即{A1,B1,C2,D1,E,F2,F3,G,H1,I2,J3,K3,L1,M2,N3}。在实际中,A1 有降噪功能,D1 有除细菌的功能,而配置方案“6”包含以上需求,验证了该模型可靠性;第二个新用户由于在高海拔地段,海拔较高,所以需要适应性非常高,其次稳定性也要求非常高。其输入为{3,2,2,3,-2,0,1,3},输出结果为配置方案“1”,即{A3,B2,C2,D2,E,F1,F3,G,H2,I1,J2,K1,L1,M1,N1}。A3 有海拔自适应、低功耗的功能,D2 有节能的功能,N1 为位置和天气自适应,而配置方案“1”含以上的需求,再次验证了模型可靠性。 本文将PSO-SVM 模型与传统SVM 模型进行对比,验证模型优越性,如表6 所示。 Table 6 Accuracy comparison between PSO-SVM and SVM表6 PSO-SVM 与SVM 的精度对比 由于测试样本数量较少,并且受样本可区分度的影响,测试样本识别率普遍高于训练样本识别率。从表6 可看出,PSO-SVM 训练识别率与测试识别率均高于传统SVM模型,PSO-SVM 模型训练样本识别率达89.84%,测试样本识别率达91.67%,可看出PSO-SVM 模型有更好的分类精度,也说明了该模型优越性。 PSS 是制造公司在面向服务转换过程中产生的新概念,也是在可持续发展背景下解决方案的发展趋势。PSS模块化配置可有效、准确满足多样化客户需求。随着人工智能的快速发展,智能技术被广泛用于协助设计和开发活动以提高竞争力。本文采用基于机器学习算法的多类支持向量机,结合历史经验解决PSS 配置问题;同时,利用PSO 算法优化SVM,以获得适当的模型参数。 通过粒子群算法优化支持向量机惩罚因子C与核函数б,将得到的最优参数代入多分类SVM 模型中,用测试集对模型进行测试。通过案例分析,证明PSO-SVM 模型分类精度比传统SVM 模型高,验证了模型准确性。最后将新客户需求作为模型输入,利用PSO-SVM 模型预测PSS 配置方案,验证了模型可靠性。不过,PSO 算法需要设置的参数过多(惯性因子、学习因子等),对自身参数设定要求过高,在一定程度上影响了寻优能力。量子粒子群优化算法可很好解决该问题,只需设置alpha 一个参数,并且运行速度更快,这是算法优化研究的重要方向之一。3.2 用于PSS 配置的多分类PSO-SVM 模型构建
4 实例分析
4.1 数据收集与编码
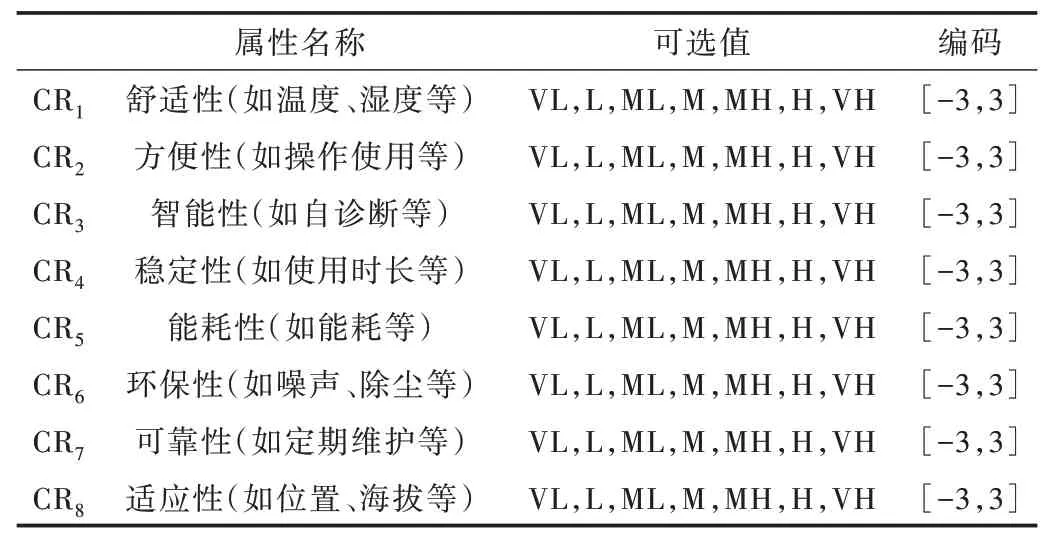


4.2 PSO-SVM 模型构建

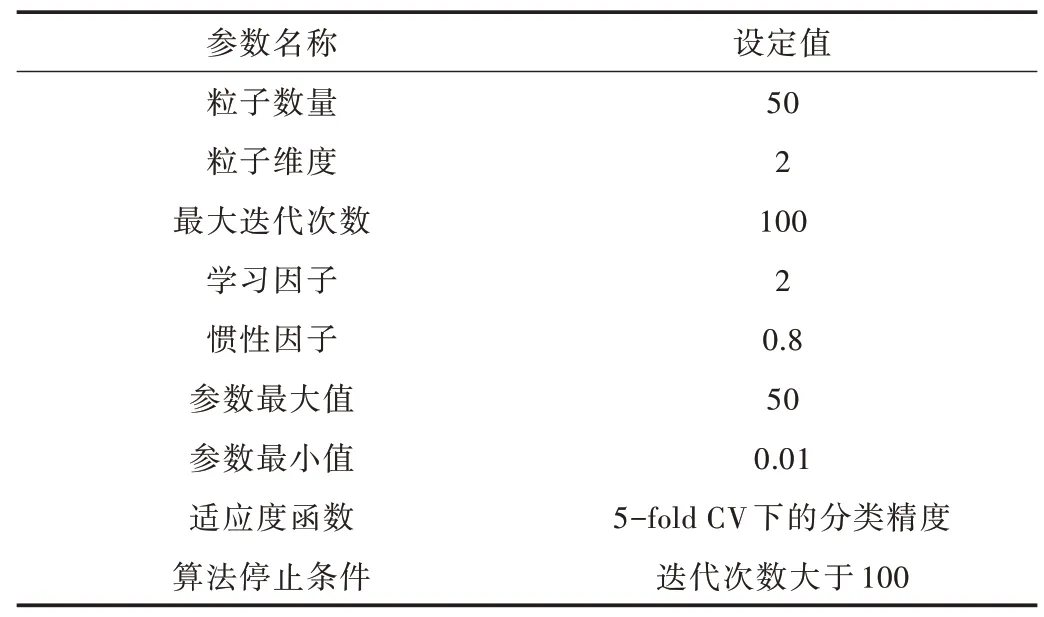
4.3 PSO-SVM 模型求解

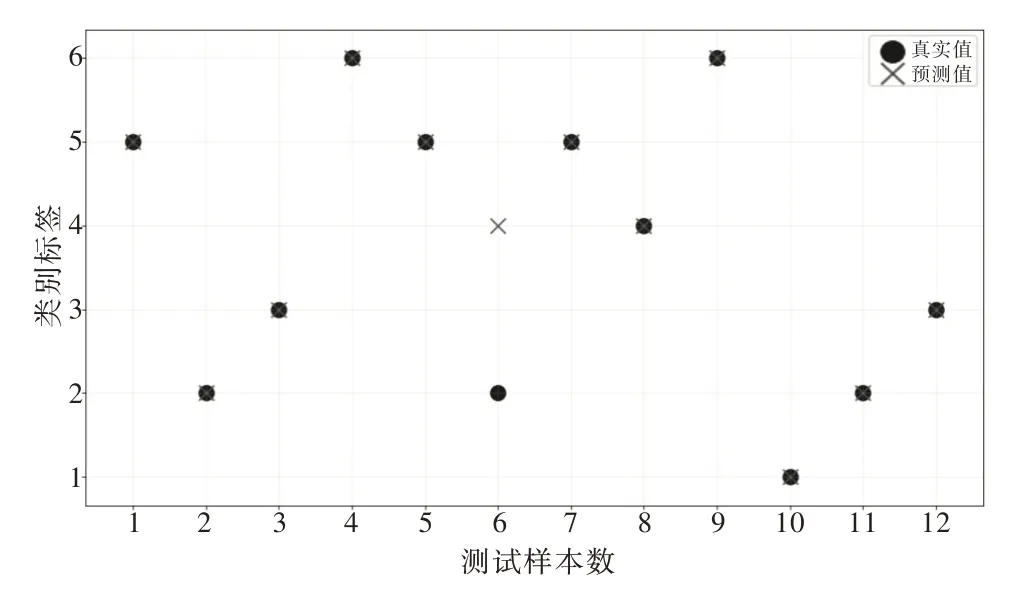
4.4 模型对比分析

5 结语
