高等数学课程思政探索及经典案例分析

刘大莲 曹彩霞 刘佳 王信峰

[摘 要]  高等數学在大学教育中属基础性学科，因其超强的逻辑性和理论的严谨性，实施课程思政较其他学科相对困难。从课程的教学大纲出发，层层深入，挖掘出课程思政在高等数学课堂教学中的六大切入点。结合课堂教学实践，提炼出部分具体课程思政案例，把思政元素自然贴切地融入高等数学课程中去。

[关键词] 课程思政;高等数学;思政元素

[中图分类号] G 642  [文献标志码] A  [文章编号] 1005-0310（2021）03-0034-05

Abstract：  Advanced mathematics is a basic subject in college education. Due to its strong logic and theoretical preciseness， the implementation of ideological and political education is relatively difficult. Starting from the course syllabus， we dig out six breakthrough points of ideological and political education in classroom teaching. Combined with classroom teaching practice， some specific cases of ideological and political education are extracted， in which the ideological and political elements are naturally and appropriately integrated into the course.

Keywords： Ideological and political education through all curricula;Advanced mathematics; Elements of ideological and political education

0 引言

课程思政是将思政元素融入高校的课堂教学中，基于立德树人作为根本任务的一种高等学校教育教学理念。《高等学校课程思政建设指导纲要》中要求：“落实立德树人根本任务，必须将价值塑造、知识传授和能力培养三者融为一体、不可割裂。”[1]也就是说，课程思政就是在传授知识和培养能力的同时，将思政元素润物细无声地穿插贴合进去，逐渐熏陶学生形成正确的三观，即世界观、价值观与人生观，这样才能在高校的教学中发挥育人功能，体现课程思政的本质内涵。在立德树人的工作中，德育比能力和知识更加重要;价值塑造是育人工作的重中之重，因此，要尽力挖掘各类课程所蕴含的思政元素，尽量做到课程思政润物无声的育人效果。

1 高等数学课程开展课程思政的必要性

北京联合大学学报2021年7月第35卷第3期刘大莲等：高等数学课程思政探索及经典案例分析作为高等院校的一门通识公共基础课程，高等数学相较于其他学科，具备授课持续时间长、覆盖学生面广的特点，因而对高校的人才培养质量及学生的未来发展有着举足轻重的影响。但长期以来，高等数学课堂教学中存在着某种程度的自然科学与人文社科知识相割裂的现象，很多教师认为，高等数学是一门纯自然学科，课堂教学应注重学科内容即数学的基础理论、基本方法及应用能力等的传授与培养，而思想政治教育应该是由人文社科类课程，比如思想政治教育类、文学艺术类等课程来完成。显然这种意识有失偏颇，忽略了育人育德这一根本任务。

事实上，对于课程思政而言，其首先要培养的就是一种正确的人生观与价值观，用科学的思维方式去认识与评价事物，各门课程都责无旁贷。尤其是在当前全球新冠肺炎疫情、科技竞争，更有意识形态不同，各种社会思潮、国家竞技等激烈交锋的背景下，我们的教育更要担负起育人育德责任，顶住压力、抵住侵蚀，进一步加强在各门课程中的思政教育，用正确的人生立场、观点和方法去教书，更要育人，为学生未来走向社会，抵制住各种错误思潮、言论，构筑起强大的内心坚定的思想防线。

课堂教学是对学生开展思政教育的主要渠道，相关部门制定高校各科教学的课堂中引入思政教育的指导纲要，非常及时且必要。这就要求一线教师要在课堂教学的内容和设计环节中有机地融入思政元素。高等数学作为高等教育中有着重大覆盖面和影响力的课程，坚定地实施课程思政势在必行。作为高校一线的数学教师，深刻理解课程思政的重大意义，深入挖掘高等数学课程内容及设计环节中所蕴含的思政元素，围绕育人目标，强化育人观念，构建多元化课程思政体系的教学实施方案，很有必要，迫在眉睫。

2 高等数学课程思政的设计思路

课程思政融入高校课堂，意味着课堂教学不仅要实现知识传授、能力培养，还要加大价值塑造的力度。现实的课程教学中往往由于课程进度、课程特点等原因而将这两者进行了割裂，特别是高校数学类课程，对知识的传授、能力的培养更为看重，价值塑造方面的涉及明显不足，当然这也与数学类课程的特点：内容多、难度大等有很大关系。课程思政要求教师要在课堂教学中积极探索思政元素实质性介入课堂教学的方式，有意识地把一些正能量的思想意识、家国情怀、行为方式等传输给学生，使之尽量避免认知和实践错误的隐性根源出现，从而对学生起到积极的引导与影响作用。

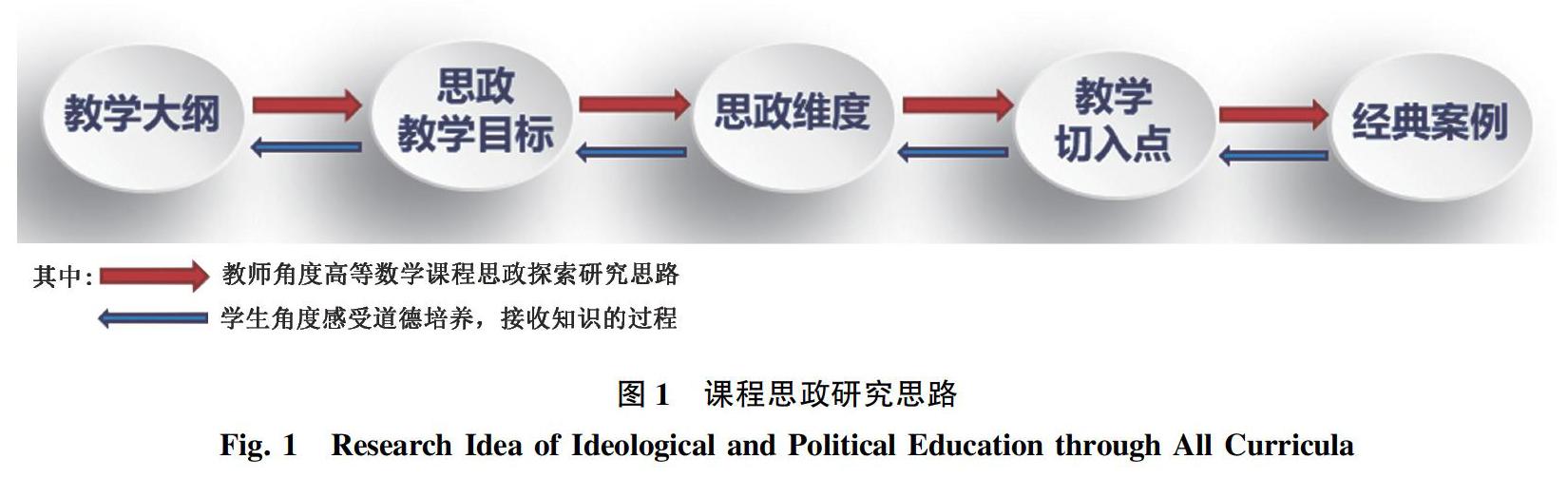
高等数学的教学如何设计，才能将非常理工思维的高等数学的讲授与思政元素无缝贴合起来，通常会考虑从以下问题入手：高等数学教学中哪些内容可以与课程思政结合？思政元素是什么？与教学大纲是否贴合？如何设计才能达到如盐入味的效果等。作为长期从事一线教学的教师，对高等数学课程的教学大纲及课程特点最为熟悉，为解决上述问题，我们就以课程的教学大纲为入手点，归纳整理出高等数学课程教学中最能体现出思政元素的教学目标，并在此基础上挖掘、梳理出课程的思政维度，从而进一步确定高等数学课程教学中的思政教育的切入点，最后基于上述理论研究，结合实际教学实践，给出部分经典案例。研究思路如图1所示。

以下将从教学大纲入手，层层深入挖掘，并对各项内容进行详细分析和阐述。

2.1 高等数学课程教学中最能体现德育思想的教学目标

通过研究高等数学教学大纲及课程特点，我们归纳整理出如下7条最能体现德育思想的教学目标：

1）从微积分产生的背景与发展历史及研究方法中，可以培养学生的科学文化修养、家国情怀、文化传承和文化自信，开拓国际视野，树立正确的世界观。

2）掌握高等数学中的基本概念、原理，培养学生科学严谨的治学态度及做人准则、正确的世界观和科学的方法论，同时开拓学生的国际视野。

3）了解高等数学在生产、生活和科学研究中的应用，了解高等数学与其他学科的交叉关系;会用高等数学的基本原理和内容知识建立数学模型，解决简单的实际应用问题，可以培养学生的科学文化修养特别是数学素养，拓宽知识面，树立正确的世界观。

4）通过高等数学内容的学习，使学生在使用数学知识解决数学题目的过程中，培养学生的计算能力、逻辑推理能力与归纳分析能力等素养，使之渐渐形成和建立科学的学习方法和思维习惯。

5）建构高等数学完整的理论知识体系与框架，培养学生良好的数学学科整体观及系统观，进而提高数学学科素养。

6）能独立自主完成高等数学的课后复习及作业，培养学生自主学习意识及踏实做人本分。

7）能够在高等数学课程学习过程中，通过同学间的讨论、合作等，学会合作和沟通，具有团队协作精神。

2. 2 高等数学课程的思政维度

从高等数学课程教学中最能体现出德育思想的7个目标，不难看出其中蕴含的思政元素，从而得出高等数学课程的如下7个思政维度，即：正确的世界观与科学的方法论、科学文化修养、文化传承和文化自信、高等数学素养、团队协作、家国情怀及国际视野[2]。在实际教学设计中，注意相关知识点与这些思政元素的有机结合，就容易做到有的放矢、言之有物。

2. 3 思政教育的切入点

经过上述分析，基于高等数学课程教学中最能体现出德育思想的7个目标及其蕴含的7个思政维度，确定高等数学教学中思政教育的6个切入点，具体如下。

1）学科发展史。通过高等数学学科发展简史的介绍，渗透科学的世界观、方法论，有助于学生形成科学的文化素养。

2）科学家简介。通过数学家的生平轶事、科研贡献简介，培养学生坚韧不拔、勇攀科学高峰的精神，了解科学家的个人奋斗与国家社会发展的关系，了解文化传承与体会家国情怀。

3）极限理论和微积分原理。其形成与应用过程，对数学思维、数学素养的训练与养成，起着非常重要的作用，并且各种定理公式和结论的形成与推导，无不渗透着严谨的方法论和正确的世界观。

4）数学与其他学科的交叉。高等数学的应用非常广泛，特别是当今世界，几乎每一个重大科技的进步都离不开数学的支撑，因此数学与很多学科都有交叉。例如在教学中我们可以用数学的方法解决一些简单的经济量化问题、物理中的连续累加积分问题等，这样有利于拓宽学生的知识面、提高数学素养，让学生感受到不同学科的科学文化素养。

5）高等数学及其应用的最新前沿。通过学习高等数学在各领域的建模应用，以及高等数学的最新应用及其进展，拓宽学生的国际视野，感受文化传承与文化自信。

6）高等数学在当代学生现实生活中的应用。可以注重学生比较感兴趣的问题，加入一些中国元素介绍，比如矩阵与兵马俑等，将数学与中国古代人民的智慧相联系，培养学生的民族自豪感和文化传承;也可以从生活细节中体会数学带给我们的人生启迪等，有利于培养学生正确的世界观与科学的方法论。

2.4 将思政元素融入高等数学课堂教学——经典案例分析

基于上述理论分析，在实际课堂教学中，从6个思政切入点入手，对高等数学课程的各个章节进行了详细的分析，在不断学习和扩大教师自身知识面的基础上，结合教学实践经验，总结出一些效果相对较好的案例。以高等数学（上）课程的部分教学内容为例，针对上述6个思政切入點，分析部分教学案例。

2.4.1 高等数学序论课——从切入点1）入手

大学生入学的第一学期，就会学习高等数学课程。他们对大学的课程与中学课程有何不同充满好奇，同时也保持着从小到大一直与数学亲密接触的亲切感。因此在开学第一节课的绪论课上有意识地向学生介绍高等数学发展史，将会对学生学习这门课程有更多的帮助。

教师通过查阅资料，课前对内容充分、准确的准备，课堂上进行详略得当的介绍，让学生体会到高等数学严谨的理论、超强的逻辑和融合在其中的数学思想的应用等，以培养学生的学科素养。

2.4.2 拉格朗日中值定理——从切入点2）入手

首先在课程引入的时候，可以先给出如图2所示的一些图片。

展示图片的同时介绍：“我们伟大祖国的首都北京——她拥有着气势恢宏的紫禁城、温婉恬静的颐和园、雄伟磅礴的八达岭长城等，举世瞩目，即便走在北京的大街小巷，也能处处体会到首都北京深厚的文化底蕴，同学们不知是否见过第4个图片中的这个过街天桥，这是位于北京珠市口的一座过街天桥，名叫数学桥。桥身上镶嵌着几个数学物理公式，看上去十分‘高大上。从左往右依次是牛顿的万有引力定律公式、爱因斯坦质能方程、拉格朗日中值公式。拉格朗日中值公式就是我们今天要讲的微分中值定理的重要内容。”这样的引入不但能提升学生对将要学习内容的好奇心，激发兴趣，同时，也蕴藏着一个思政元素——思政点1：将日常生活中祖国特有的物质文化元素引入课程中，潜移默化引导学生热爱祖国，爱首都，增加民族自豪感，培养学生家国情怀，符合上述第6）切入点。

其次，可以简单介绍拉格朗日生平：“约瑟夫·拉格朗日（Joseph-Louis Lagrange，1736—1813），法国著名数学家、物理学家。他在数学、力学和天文学3个学科中都有历史性的重大贡献。17岁时，他迷上了当时正发展迅猛的数学分析，开始专攻。18岁时，拉格朗日写了第一篇论文，寄给了数学家欧拉，但却获知这一成果早在半个世纪前就被莱布尼兹取得。这个并不幸运的开端并未使拉格朗日灰心，相反，更坚定了他投身数学分析领域的信心。”从故事中让学生获取思政点2：遇到挫折不要灰心气馁，困难与挫折是人生常态，要有越挫越勇的精神，体现第2）切入点。

第三，在讲授拉格朗日中值定理之前，要回顾罗尔中值定理并指出其重要性，在讲授拉格朗日中值定理之后强调拉格朗日中值定理的出现在理论和实际应用中都占据着重要的地位，然后引出柯西中值定理，在3个中值定理的两次衔接及最后的课程总结中贯穿强调：“尽管前人的研究成果已经很耀眼，但数学家们却并没有止步于别人的研究成果，他们继续钻研、整理并完善前人理论，进行更深入的研究与探索。”从而融入思政点3：希望同学们能够学习科学家们不止步于现有成果、不断钻研、勇于创新的精神，也许下一个重要的定理就是以你的名字命名的呢！

2.4.3 定积分的定义——从切入点3）入手

积分学部分的思政元素也很多，比如在讲定积分的定义时，我们要将“分割、近似、求和、取极限”的数学方法传授给学生，同时更重要的是让学生理解、掌握“以直代曲，以不变代变”的转化思想，“化整为零，合零为整”的“微元法”的数学思想等，体会其中严密的逻辑推理过程;让学生今后会用数学方法和数学思想去解决理论研究和生活实际中的问题，同时让学生体会到数学学科严谨背后的灵活、理性背后的生动，感受高等数学思维教育方面的独特魅力。

2.4.4 函数的最大值与最小值——从切入点4）、5）、6）入手

求函数的最大值与最小值在当今的社会生产中应用非常广泛。此处可以介绍数学的前沿学科：“有一门专门研究求函数最值的学科叫最优化理论与方法。最优化，就是在一定的约束条件下，使系统具有所期待的最优功能的组织过程，是从众多可能的选择中做出最优选择，使系统的目标函数在约束条件下达到最大或最小[3]。而说到最优化，就不得不提起我国著名数学家华罗庚先生。华罗庚先生就曾在工农业领域大力推广过优化方法，在特定的历史时期，创造了经济效益，是我国最早把数学理论研究和生产实践紧密结合做出巨大贡献的科学家。华罗庚因家境贫寒，所以基本上是自学成才。因为他在数学上做出了巨大的成就，被称作‘天才数学家。对于这种称呼，他这样回答：‘所谓天才，就是靠坚持不懈的努力。”这段介绍不仅可以向同学们初步介绍最优化方法，对前沿学科有所了解，还介绍了伟大科学家华罗庚先生，增强学生的民族自豪感，鼓励学生养成刻苦钻研、不懈努力的优秀品质。任课教师也可以将最优化与学生的专业相结合，比如如果授课对象是计算机专业的学生，就可以告诉他们机器学习中众多的经典方法如支持向量机（SVM）以及现在大数据挖掘中应用较广的对抗神经网络（GAN）等，最终建立数学模型后都是一个最优化模型，就是求目标函数的最大值最小值的问题。鼓励学生学好数学，为专业学习打好坚实的基础，将来投入到科学的创新中，为祖国贡献自己的一份力量。

2.4.5 微分方程部分——从切入点1）、5）、6）入手

在此部分知识的第一次课中，同样可以适当介绍微分方程的起源和发展史，同时让学生了解到，微分方程可以解决现实生活中的很多问题，比如在大学生数学建模选修课中，微分方程就是一种很好的解决实际问题的方法。在授课过程中，可以结合很多实例，展开知识讲解，并融入课程思政元素。长沙理工大学的吴烨老师提出，在讲到可分离变量微分方程的时候，可以借助引例“中国航母如何解决战斗机安全滑行距离”这一问题，通过视频，简述中国海军自主研制航母的历程，突出中国海军“特别能吃苦、特别能战斗、特别能奉献、特别能公关”的精神，借此对学生进行爱国主义教育[4]。

3 结束语

课程思政，其实并无定法，但鉴于课程特点，却也有章可循。本文首先分析了高等数学课程思政的必要性，基于高等数学教學中最能体现出德育思想的7个教学目标分析得出高等数学课程思政的7个思政维度，并据此给出高等数学课程思政的6个切入点，随后相应地列举了高等数学（上）的部分内容思政案例。从所举案例不难体会，基于课程特点的6个切入点在具体实施课程思政的时候给了我们很大的启示，有的放矢，高等数学的课程思政不再那么抽象。而这些切入点并不孤立，经常一个知识点内可以同时出现多个思政元素，相互溶解、渗透。

除此之外，身边发生的时事新闻，我们生活密切相关的临时性事件，甚至当前学生关注的电影、流行歌曲，都可以是我们课程思政的入手点。作为数学老师，只要遵循课程思政的初衷，充分利用学科优势和课堂面对面教学的优势，利用课上教学、课间休息、课下答疑等任何时间，都可以进行思政教育。只要课程思政的思想融入授课教师的心中，就不受时间、空间和形式的约束。课程思政无处不在，却又无迹可寻，既拉近了与学生的情感交流，又能达到润物细无声的效果。

课程思政，没有最好，只有更好。如何进一步将高等数学的课程思政做到更好，还需要大家共同进行深入研究、实践和探索。

[参考文献]

[1] 教育部关于印发《高等学校课程思政建设指导纲要》的通知[EB/OL].（2020-06-03）[2021-04-25]. http：//www.moe.gov.cn/srcsite/A08/s7056/202006/t20200603_462437.html.

[2] 孙艳辉，南俊民，马国正，等. 物理化学课程思政教学设计与实践[J].大学化学，2021，36（3）：217-222.

[3] 刘建明，王泰玄，谷长岭，等.宣传舆论学大辞典[M].北京：经济日报出版社，1993：3.

[4] 吴烨. 高等数学“课程思政”案例教学实践：以“可分离变量方程”为例[J]. 教师，2020（20）：43-44.

（责任编辑 李亚青）