校园供水系统智能管理分析及优化

李 琳

（川北幼儿师范高等专科学校 初等教育系，四川 广元 628017）

近年来，校园用水占比逐年增加，同样，在水资源的浪费上也不可小觑.随着时间的增加，校园供水管网出现老化，会出现漏水情况，尤其是地下水管暗漏，是极其不容易被发现的[1].通过数据分析，了解各个时期，各个功能区用水情况，及时发现和解决智能供水系统中存在的问题[2]，减少不必要的人力、物力和财力，维护良好的公共供水网络，减少用水的漏损，并采用较为合理的方式进行漏损水表的维修.对于学校来说，修理老旧管网是一件耗时、耗力、耗钱的事情，经过数据分析和模型建立，可以及时发现管道漏水，同时能节省不必要的人工费和材料费.智能水表已在学校普遍使用，可以实时获得供水系统运行数据.根据某校区2019 年全年水表的层级关系，所有水表四个季度(以15 分钟为间隔)的读数，利用已知的数据，建立数学模型来解决以下问题:

问题1:统计并分析各个水表的变化规律.对校园进行功能分区，根据统计数据分析不同区域的用水特征.

问题2:按附件-水表层级图①把所有水表分为四个层级，利用spss 对各层级数据进行相关性分析，在此基础之上，建立线性回归模型并分析模型误差.

问题3:利用附件数据建立数学模型，计算该校区漏水率.若漏水率不大于5%，则该校区供水网络运行良好，反之该校区供水网络存在问题.

问题4:在问题3 的基础上，进一步定位发生漏损的水表位置，利用已有数据检测漏水点中的暗漏点.

问题5：调查市场水价、管网维修成本，利用已有数据，分析问题4 中已检测的各个漏水点.

1 基本假设

假设一：在计数期间，水表运转正常，水表读数无误.

假设二：附件中出现水表无读数的数据，默认此段时间该水表的用水量为0.

假设三：天气、温度等自然灾害及其它特殊情况对水表读数产生的影响忽略不计

假设四：学校重大活动用水、学生放假离校对用水量产生的影响忽略不计.

2 问题分析

2.1 问题一的分析

首先需要对已有数据的有效性进行分析，修正无效数据，统计分析出该校区2019 年每日用水总量并绘制出每日用水总量与时间的折线统计图，描述该校区2019 年用水量的整体情况.然后按季度统计每个水表每天的用水量，筛选出每个季度用水总量排名前10 的水表数据绘制折线统计图分析水表数据的变化规律.再查阅文献，对校园进行功能分区，统计分析不同功能区每月用水情况，最后随机抽取10 天分析每个功能区每天的用水“高峰”.

2.2 问题二的分析

根据附件-水表层级，按层级分别筛选出每个水表每日用水量并计算出每月的总用水量.利用spss 对每个层级内变量的相关性进行分析，根据分析结果，利用多元线性回归模型分别找出各层级变量之间的关系，编写程序，利用matlab 计算模型误差.

2.3 问题三的分析

对已有数据进行处理，统计每个水表每月的用水量，建立数学模型，编写程序，利用matlab 计算管网漏水率.

2.4 问题四的分析

在问题3 的基础上编写程序，利用软件找出管网漏损的位置.查阅文献，利用附件信息定义并查找暗漏点.

2.5 问题五的分析

基于前四个问题的结论，收集市场数据，对管网维护情况进行具体分析，进而确定管网漏损的最优维修决策方案.

3 问题一求解

3.1 数据的预处理

附件-第一季度共729283 条数据，在假设一的前提下，有53476 条数据有误；附件-第二季度共778195 条数据，在假设一的前提下，有52921 条数据有误；附件-第三季度共791844 条数据，在假设一的前提下，有62576 条数据有误；附件-第四季度共787466 条数据，在假设一的前提下，有82753 条数据有误，修正数据，使“用量=当前读数-上次读数”.共791844 条数据，在假设一的前提下，有62576 条数据有误；附件-第四季度共787466 条数据，在假设一的前提下，有82753 条数据有误，修正数据，使“用量=当前读数-上次读数”.

3.2 数据分析

基于以上数据，统计出每个水表每日用水量,用excel 统计出该校区2019 年每日用水总量，并绘制出每日用水总量与时间的折线统计图.由图分析可知，二月为该校用水量的“低峰期”，最低值出现在 2019 年 2 月 8 日，为 702.4m³，四月为该校用水量的“高峰期”，最高值出现在2019 年 4 月 24 日 ，为 19632.7m³，其余月份用水量较为平稳.因此学校为保证供水系统正常运行需在四月加强水压稳定，保证平稳度过用水“高峰期”.经查阅，适当提高变频供水的压力设定值为保证水压最经济的解决办法[3].

分季度统计每个水表每日用水量，筛选出各季度用水总量排名前十的水表数据，绘制折线统计图，见图1.

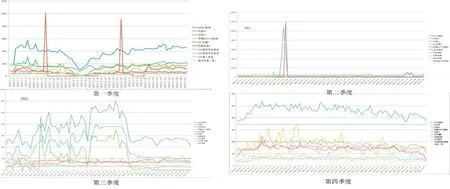
图1 各季度用水总量排名前十的水表用水量走势趋图

由图1 可知，在第一季度用水量排名前十的水表中 XXX 花圃在 1 月 19 日 、2 月 26 日用水量突然增加，增加量显著，可能出现漏水现象.XXX 第五学生宿舍在第一季度中用水量明显整体高于其它水表用量.在第二季度用水量排名前十的水表 中 ，xxx 体 育 馆 在 4 月 24 日 ，区域 4 在 4 月 23日,用水量突然增加，增加量显著，可能出现漏水现象，其余水表在当季度用量整体平稳.在第三季度中，校医院南,xxx 宾馆，xxx 第二食堂的用水量波动幅度较大且明显高于其它水表.

在第四季度中，64397 副水表每日用水量均高于其它水表，养殖队6721 副表的用水量波动较大，其余水表较平稳.

统计每个水表每月的用水量，可知各个季度均统计了91 个水表数据，对比各季度每个水表的用水量，发现：水表名为“消防”的数据未出现在第一季度，水表名为“教育超市+”的数据仅出现在第一季度，故该校园一共有92 个水表.

查阅文献[4]，结合实际情况，按功能把校园划分为四个功能区:宿舍、办公、休闲娱乐、其它，结合附件-水表层级，进一步把本题中所有水表按区归类见表1.按功能区提取各个水表每月用水量，按月统计各个功能区所有水表用水总量，绘制折线统计图，见图2.统计分析各个功能区每月用水量的最大值、最小值、平均值、标准差，见表2.

表1 水表功能分区表

图2 每月各个功能区所有水表用水总量折线统计图

由图2、表2 可知：四个功能区每月用水量由高到低排序依次为：其它、生活休闲、宿舍、办公.月用水量最大出现在生活休闲区，为27140.94m³，月用水量最小出现在办公区，为3169.92.生活休闲区的月用水量变化波动较大，宿舍、办公区月用水量波动不明显.

表2 各个功能区每月用水量的描述性统计分析

4 问题二的模型建立与求解

4.1 数据分析

根据附件-水表层级，按层级提取各个水表每月的用水量数据，利用SPSS 依次对第一层级、第二层级、第三层级、第四层级每个水表每月用水数据进行相关性分析，进一步分析spss 运算结果可知：对于第一层级，水表名为“64397 副表”的水表与其它量的相关性较好，分析结果见表3，故可以考虑以此量为因变量，其余量为自变量进行多元线性回归分析.对于第二层级，水表名为“新留学生楼”的水表数据与其它量的pearson 显著值均大于0.1，说明此量与其它量的相关性不明显，若要进一步做多元回归分析，则应剔除此量.对于第三层级，存在多个与其它量相关性不显著的变量，故在做多元回归分析时应剔除这些量.对于第四层级，观察相关性分析结果，发现水表名为“XXX3 舍热泵热水”的水表、“XXX4 舍热泵热水”水表、“XXX5 舍热泵热水”水表之间相关性较好，“茶园+”与其它量的相关性不明显，分析结果见表4.

表3 第一层级水表相关性分析结果表

表4 第四层级水表相关性分析结果表

4.2 模型的建立

基于以上数据分析，确定用多元线性回归建立模型,由于方法类似，在此以第一层级、第四层级为例，具体分析.由表3 知，第一层级以“64397副表”为因变量，其余变量为自变量.

由表4 知，第四层级可以“XXX5 舍热泵热水”为因变量，其余变量为自变量，建立模型：y=b0+b1x1+b2x2.

4.3 模型的求解

编写程序，通过MATLAB 软件对该模型的回归系数b 进行求解，结果见表5.即：

表5 回归分析结果统计表

求得第一层级模型误差为6.88%，第四层级表用水量的相对误差为7.23%，模型拟合较好.

在计算出相关系数b，残差r 后，绘制出一层级残差图3、四层级残差图4，一级表线性回归图5、四级表线性回归图6.

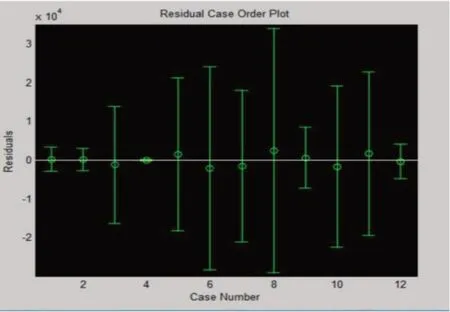
图3 一级表残差图

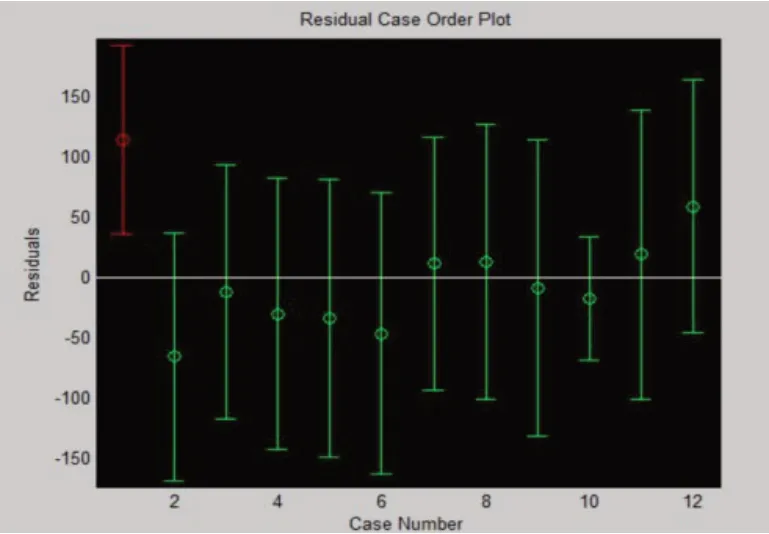
图4 四级残差图

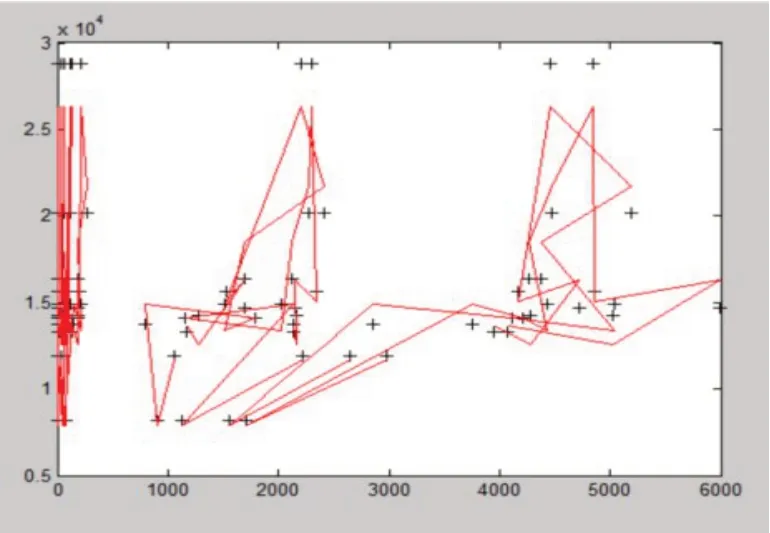
图5 一级表线性回归图

图6 四级表线性回归图

5 问题三的模型求解与检验

5.1 数据的预处理

要统计出水管漏水情况，需对每一个水表进行核查，考虑到若以天为单位进行计量，很难通过水表核查出漏水量较小的出水口，故以月为基准统计出每个水表的用水量.在已有数据之上，进一步统计每个水表月用水量，共有92 个水表，应有92 条数据，因水表名为“消防”的数据未出现在第一季度，共计用水3m³，故在此次数据处理过程中删除此条数据.

5.2 模型的建立

给出判定漏水的标准:月用水量>（月平均数+2×标准差）时，判定为漏水.

漏水量计算公式：漏水量=用水量-（月平均数+2×标准差）

定义漏水率衡量漏水的程度：漏水率=漏水量/用水量×100%

计算出每个水表的月平均用水量和标准差，在MATLAB 中编写程序，统计漏水的量，用公式计算漏水率，程序计算出漏水率为7.66%.

5.3 模型的求解与检验

编写程序，通过MATLAB 软件，计算出漏水率为7.66%，进一步分析漏水点，再回去检验筛查后的数据表，发现新留学生楼、xxx 毒物研究所、xxx中心水池、教育超市+用水量在后面月用水量有为0 的情况出现，当存在水表漏水而没有维修的情况下，不可能出现月用水量有为0 的情况，即排除水表漏水，对这四个漏水异常点进行修正，修正后的漏水率为7.23%.

6 问题四的模型建立与求解

由问题三可知，编写程序，通过MATLAB 软件，可以找到水表发生漏损的位置，筛选出修正后的漏水点共56 处.经查阅，地下暗管的口径通常大于75mm[4]，结合附件-水表层级中的口径数据,进一步筛选出口径大于75mm 的水表，见表6，认为这些水表处很可能发生水管暗漏.

表6 漏水点异常表

7 问题五的模型建立与求解

7.1 数据的收集与整理

问题四已求出漏水管，故需要维护的管网共56 处.问题三已给出漏水量计算公式：漏水量=用水量-（月平均数+2×标准差），利用excel 可以计算出每个漏水管的漏水量.考虑到学校实际用水需要，宿舍、医院、食堂、污水处理、xxxx 舍热泵热水为“必修”网管，共计11 个.长期考虑，筛选出漏水量大于4000m³的水表有必要维修，共计18个，计算出其花费.

通过以上分析，可以计算出选修水表网管点27 个.经调查，本校所在地级市水价为2.86 元/m³,故一年漏掉的水费=漏水量×2.86.《建筑质量工程管理条例》规定水管的维护年限一般2 年，本题在计算时默认水管保质期为2 年，则把维修费与两年漏水费相比较，当两年漏水费＞维修费时，则选择修，当两年漏水费＜维修费时，则选择不修.

7.2 问题求解

利用excel 筛选出选修水表网管点27 个，计算维修花费及2 年该水管的漏水费，判断是否维修.

8 结语

本文中的模型主要解决校园供水系统的问题，已解决了如何确定供水管道漏损量及漏损位置等问题.该类模型还可以用于生活中的供电系统、供气系统等智能管理.

(1)对具体情境中可能出现的多种情况进行分析，使建立的模型更加优化.在问题二中，详细观察和分析附件中的数据，运用多元线性回归模型，能够很好的拟合出需要的数据.

(2)采用相关性分析得出数据的有效性更高.把抽象的大量数据转化为具体的图像或模型，从而更简明的揭示出问题的本质，帮助问题的解决.

(3)在对数据进行处理的过程中，对有些数据的采用比较理想化，使结果存在一定的局限性.

(4)由于所给部分数据的约束以及数据量过大，有些因素可能没有考虑到.

注释：

①网址：https://www.mcm.edu.cn/html_cn/node/10405905647c52abfd6377c0311632b5.html.