探究区间估计与假设检验的关系
2021-08-23朱海
朱 海
(重庆工商大学 数学与统计学院,重庆 400067)
1 背景与意义
近年来,有很多国内外学者都研究了区间估计与假设检验的关系.学者吴纯[1]通过证明提到:“一般情况下,利用假设检验可以建立区间估计,反之亦然”、“假设检验和区间估计的结果在解释上可以有差别”等结论,告诫大家统计学上的结论一定要注意其实质,不能只停留在问题表面;学者王建华[2]通过论证,纠正了“区间估计和假设检验是统一的,是一个问题的两个方面”这个似是而非的说法,说明了区间估计和假设检验既有联系,又有区别;也有学者通过“顺推法”和“反推法”[3]进行区间估计和假设检验关系的研究,最终确定了两者的区别和联系.现在,区间估计和假设检验的应用极为广泛,去年国外一篇论文发表出来,论文题目为:In‐fluence of multiple hypothesis testing on reproducibility in neuroimaging research: A simulation study and Python-based software[4],讲的是神经影像研究中多重假设检验对再现性的影响,整篇文章围绕假设检验进行了一系列模拟分析,这从侧面说明了假设检验应用范围之大.
本文对区间估计和假设检验的关系探究源自教材《概率论与数理统计教程第二版》(茆诗松,高等教育出版社,2011 年)中数理统计部分,该书在介绍参数估计和假设检验时,很多知识点覆盖面很广,但都只是单一的指出基本概念,至于其中多种统计推断方法是否有联系并未做过多介绍,比如在谈及区间估计和假设检验的关系之时,所用篇幅较少,只是谈及了区间估计时的枢轴量和假设检验时的检验统计量相同并非偶然,当然,枢轴量和检验统计量的相同的确很大程度的说明了区间估计和假设检验的关系匪浅.但是,区间估计和假设检验关系仅仅如此吗?区间估计中的置信水平和假设检验中的显著性水平有联系吗?区间估计和假设检验方法选择有啥参照吗?本文在此基础上,大篇幅地探究了两者的关系,包括区间估计和假设检验的基本概念、应用方面、优劣方面、联系及不同以及相关问题的深度剖析,都进行了总结和讨论,并通过一些例子对一些问题进行举例论证,并查阅了一些相关书籍和文献,整理结论并讨论,使得大家对这两种统计推断方法更加熟悉和深层次了解,一定程度上,能够帮助读者在处理相关问题时避免一些错误.
2 区间估计和假设检验的基本论述
2.1 区间估计概念
区间估计,顾名思义,是包含一个区间的估计,这个区间是用来度量一个点估计的精度.参数的点估计经计算得到了一个具体的数值,这样一个具体的数值方便计算和使用.但计算出来的点估计精度如何,点估计本身并不能说明,需要依靠对应的分布去反映,现实中,我们通常用一个区间去覆盖已知的点估计,也可以说求得点估计的取值范围,它应该是一个区间,下面给出具体定义[5]:
设θ是总体的一个参数,x1,x2,…,xn是样本,求得统计量θL(x1,x2,…,xn),θU(x1,x2,…,xn),使得θL<θU,得到样本观测值之后,便把θ估计在区间[θL,θU]内 . 由于样本具有随机性,区间 [θL,θU]覆盖参数θ的可能性并不确定,这里通常需要我们人为给定一个概率,诚然,我们肯定想区间覆盖θ的概率P越大越好,但是这必然会导致区间长度增大,这里把区间[θL,θU]覆盖住θ的概率给定为 1 −α,则有Pθ( )θL≤θ≤θU≥ 1 −α,则 称随机区间[θL,θU]为θ的置信水平为 1 −α的置信区间,θL和θU分别称为θ的(双侧)置信下限和置信上限.
2.2 置信区间计算方法
通常,要计算置信区间,一个最常用的方法就是枢轴量法[5].对于这种方法,寻找置信区间最关键的步骤就是要找准未知参数所对应的合适的枢轴量,这里记G为枢轴量,构造一个样本和未知参数θ的函数G(x1,…,xn,θ)使得G的分布不依赖于未知参数θ.另外枢轴量的寻找一般从θ的点估计入手.
区间估计适用范围:在参数的点估计不易计算,或者探究点估计精度如何时,区间估计往往能起到至关重要的作用,它能够指定概率(即置信水平)求得相应比较精确的区间进行估计,这些都是点估计无法做到的.例如众多分布中最常用的双参数正态分布,记正态总体为N(μ,σ2),在一个参数已知,另一个参数未知时,都可以求得未知参数对应的置信区间,得到对应的区间估计.
2.3 假设检验概念
所谓假设检验,顾名思义,就是一个检验假设是否成立的过程,又称统计假设检验.它是用来判断样本与样本之间、样本与总体之间的差异到底是由抽样误差引起,还是由样本之间本质差异造成的一种统计推断方法.假设检验有很多方法,显著性检验作为一种最常用的假设检验方法,其基本原理是先根据一些非样本信息对总体某个参数做出某种假设,然后通过对抽样信息的统计推理,对这个假设是否应该被拒绝做出判断.一些常用的假设检验方法有Z检验、T检验、卡方检验、F检验等.一个很经典的假设检验问题,例如女士品茶试验[5],女士每次猜对的概率为0.5,10 次都猜中概率为 2−10,很小的概率,几乎不可能发生的事件,竟然发生了,这样一个小概率原理,伟大的费希尔对这一试验诸多细节进行研究,最终形成了假设检验理论.
2.4 假设检验的基本步骤
ⅰ.建立假设:根据要求对参数设置原假设H0和备择假设H1.如一对假设为
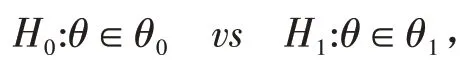
原假设有简单原假设和复杂原假设,相应的备择假设也有简单备择假设和复杂备择假设之分,其界限是考虑到假设里面θ0和θ1所包含的点的个数.因而整个假设又有双侧假设和单侧假设之分.
ⅱ.选择检验统计量,给出拒绝域形式:记W为检验的拒绝域,而Wˉ为检验的接受域.
ⅲ.选择显著性水平:一个是α,称犯第一类错误(也称弃真错误)的概率;另一个是β,称犯第二类错误(也称纳伪错误)的概率.
ⅳ.确定拒绝域:根据假设单侧或双侧检验,给出相应的拒绝域.
ⅴ.进行判断:通过样本观测值,观察相应参数值是否落在给出的拒绝域内.
2.5 假设检验 p 值与 α 的关系
(1)检验的p值:一个假设检验问题中,利用样本观测值能够作出拒绝原假设H0的最小显著性水平.每一个假设检验问题都对应一个确定的p值.
(2)检验的p值与人们心目中的显著性水平α进行比较可以对假设检验做出判断:
ⅰ.若α≥p,则拒绝原假设.
ⅱ.若α 区间估计主要是根据一个样本的观测数据得到参数的估计范围,在这个范围内,参数落在区间中的概率已知(一般人为给出),不仅能够很直观的检验对未知参数所做的点估计的准确性,也可以在大样本的情况下对参数进行估计,所得到的估计值应落于所得到的区间内;而假设检验首先则主要是对总体参数做出一个假设,然后利用样本信息和相关检验统计量的分布特征去检验这个假设,最终做出是否接受原假设的结论.如此看来,区间估计和假设检验在主要功能方面还是有交叉之处,都可以对参数的准确性进行判定.但要说明的是,假设检验是统计推断中的一项重要内容,它是根据原有资料作出一个对总体指标的限定,某一随机变量是否服从某种概率分布的假设,然后利用样本数据,采用合理的统计方法,计算出相关假设的检验统计量,然后依据小概率事件原理,以较小的风险度去判断估计值与总体值是否存在显著差异,是否应当接受原假设的一种检验方法.但是,在面对样本指标和总体指标时,一味地用样本指标去估计总体指标,其结果并非完全可靠,换句话说,对于诸多假设检验问题,不同问题具有不同程度上的可靠性,需要我们进一步对检验结果去加以检验和论证.通过对问题的检验,对样本指标与总体指标之间是否存在差异作出正确的判断,是否应该接受原假设.当然,这里也必须明确,进行假设检验的目的不是验证样本指标本身是否出错,而是为了分析样本指标与总体指标之间是否存在显著差异.从这个实际意义出发,假设检验又称为显著性检验,这在统计学意义上与区间估计有所不同.区间估计重在估计,是参数估计的一项重要内容,它为总体参数服务,但凡数理统计书中,首先总是会引入统计量的概念,让学者们第一时间弄懂统计量的相关知识,其目的在于对一些深层次问题进行统计推断,而在实际生活中,我们往往会向众多分布中的未知参数靠近,这样一来,区间估计出现也不足为奇了. 区间估计不仅是统计推断中的重要内容,也可以应用于抽样推断.根据区间估计和假设检验的定义以及步骤来看,对于这两种统计推断方法,在应用领域方向,不仅仅是书本上的理论推理,现实中也可以运用于科学研究、医疗卫生、金融投资等各个方面.但是若真要比较两种方法的用途谁广泛,还真得分类讨论.对于区间估计来说,它是一个非常依赖样本信息的一种推断方法,样本信息包含越全面、越准确,得到的置信区间也就越精确,这样一来,便对研究者提出了要求,如果样本信息量足够说明真实情况,此时使用区间估计便没什么问题.对于假设检验而言,首先在人们拿到一个假设检验时,必须根据需要设置一对假设,原假设H0和备择假设H1,然后根据得到的数据信息,对假设进行判断.然而,假设检验人为的确定的假设必须要避免偏差,否则会对结果产生巨大影响,甚至可能导致判断偏差.假设检验一般而言是研究者偏向于拒绝域进行统计推断方法,由于原假设与样本信息无多大关系,故而假设检验对样本信息的敏感度没有区间估计那般强烈.综上,区间估计和假设检验的应用各有侧重,当研究者所研究的问题需要确切的样本信息时,这时候选择区间估计较好;当研究者所研究的问题需要较多非样本信息(如前人经验、无法看做样本信息的信息)时,建议选用假设检验. (1)区间估计属于参数估计的一种,参数估计是以样本数据为基础,进而去准确的估计总体参数的确定值;然而假设检验则是以样本数据的相关信息去检验总体参数原始假设是否成立. (2)区间估计事先需要给定一定概率(也称置信水平),区间估计要求概率越大越好,得到的估计区间会更加精确;而假设检验是在小概率原理上立足的,最终所求的概率p值越小越显著. (3)区间估计最终得到的是双侧置信区间;而假设检验会根据题意确定双侧检验或者单侧检验. 通过下文区间估计和假设检验应用举例可以看出,区间估计所使用的枢轴量与假设检验所使用的检验统计量是一样的.这是为什么呢?现从假设检验的右侧、左侧、双侧分三种情况进行讨论(假设σ已知,样本为x1,x2,...,xn来自正态总体N(μ,σ2): 3.4.1 右侧检验 3.4.2 左侧检验 3.4.3 双侧检验 综上所述,正态总体参数的置信区间与假设检验问题的检验存在非常密切的联系,枢轴量与检验统计量的相同不是偶然,而是这两种统计推断方法中存在一一对应关系,两种问题可以相互转化,假设检验问题能够成为区间估计问题,区间估计也能够成为假设检验问题. 3.5.1 置信区间误区 以下文例1 为例,有些熟悉区间估计定义的人可能会说:“题中得到的95% 置信区间为[12.282,12.518],它是以0.95 的概率覆盖总体均值(即题目中的平均长度)”,其实,仔细琢磨,这种说法欠妥.为什么呢?因为在这里,如果换成是在大量样本中得到的置信区间,只能说大约95%会覆盖总体均值,题目中只是由一个样本得到的置信区间,到底包含或者不包含总体均值,没有概率可言.我们都知道,总体均值其实是一个固定的数值,而求得的置信区间也是一对固定的数值,这里不存在随机变量,故而不可能存在覆盖的概率,最初的随机区间一旦实现,就变成了两个固定数字,便失去了随机性,进而也无法谈及概率. 3.5.2 假设检验误区 (1)大家都知道,做假设检验的目的是从假设中找到需要的答案,所以说拒绝原假设的显著性水平α的选择很重要[6].抛开书本理论,选择α时必须与实际问题相结合,具体问题具体分析,课程当中的例子过于理想化,很多影响问题的敏感因素都未曾给出,但是在实际生活中往往缺乏可信度.比如警察在通过DNA 或者指纹去判断作案凶手、血缘关系时,对于这种非常敏感的问题,α取值稍微过大,都会使得到的结果可信度大打折扣,此时α应该是一个非常小的数.相反,如果实际要求α不宜过小,α就应该取相对大,否则,一些大的影响因素可能就会错过.总之,α的大小选择并不能简单的全默认看成是0.01、0.05、0.1,应该灵活处理. (2)通常我们在面对假设检验结果的时候,认为落入了拒绝域,则表示拒绝原假设,这个判断没有错误;但是反之,当我们不能拒绝原假设的时候,很多人就会很自然的认为应该接受原假设,这便是不够严谨了.举一个例子如下:判断一个罪犯是小偷,设置原假设为H0:不是小偷,备择假设H1:是小偷.当在小偷身上或家里发现别人的东西,在几乎不太可能( )p→0有一模一样的东西的前提下,这时候就拒绝原假设:不是小偷,认为他是小偷.当在小偷身上或家里没有发现别人的东西,就说明没有证据说明拒绝原假设:不是小偷,但是这不能说明小偷从未偷过东西,只是证据不足而已.因此,证据不足接受原假设和实际上就接受原假设是有差别的. 例:某公司规定一批零件直径为10cm时为合格,现在随机抽取50 个零件作为样本进行检测,根据样本数据显示,得到样本均值xˉ= 10.2,已知标准差为0.4,假设取α= 0.05,检验这批零件是否合格. (1)区间估计法 (2)假设检验法 根据题意设置假设 :H0:μ0= 10vsH1:μ0≠ 10 , 综上可知,在同样的显著性水平下,区间估计和假设检验的结果一样,说明这两种方法可以相通. 5.1.1 区间估计中 显著性水平是估计总体未知参数落在某一区间内的一个概率,也表示为可能犯错误的概率,一般用α表示,但是,通常以置信水平(1 −α)为盖住区间的概率而被我们事先给定. 5.1.2 假设检验中 根据人们做判断时误判的错误类型,将犯第一类错误概率(即弃真错误)叫做显著性水平,用α表示 . 相同问题条件下,区间估计中1 −α置信区间问题与显著性水平为α的假设检验问题一一对应,且判断结果相同. 假设检验过程中,在选择显著性水平时,引入了两类错误:第一类错误(弃真错误),用α表示,第二类错误(纳伪错误),用β表示.任何一个假设检验问题,我们不可能找到一个检验同时使这两类错误都尽可能小,只能选择其中一种错误,让它尽可能小.书中引入功效函数[7]进行说明两类错误的关系,结果是α与β中一个减小必然导致另一个增大,但是α+β并不一定等于1,且这个结论具有一般性.那么为什么要选择α作为显著性水平,而不是β呢?原因有以下几点: (1)从心理学角度来看,第一类错误为弃真错误,认为本来原假设是真的,却被拒绝,这会让人懊悔不已;第二类错误为纳伪错误,认为原假设不是真的,却被接受,这种错误即使发生了,顶多就说判断错误,或者说找“学艺不精”的理由,相对来说,犯第一类错误更不能让人接受;从现实危害角度来看,犯第一类错误可能会产生巨大影响,它的不良后果会更加大于犯第二类错误,比如所有人都犯了第一类错误,后面人可能一直无法找到真的;相反,犯第二类错误之后,如果重新设计实验便可能快速发现问题所在. (2)一般而言,第二类错误概率对具体参数要求颇高,相比较于α来说,β在不少场合不容易求出,产生β的原因多与实验设计、样本数据、处理效应等因素有关,α更容易被计算出. 此处对显著性水平的进一步分析并非偶然,而是通过对显著性水平的了解,我们能够对区间估计和假设检验的关系更加明确,虽说两处定义不一样,但是只有在α一定的情况下,研究区间估计和假设检验才有价值;再者显著性水平的选择存在很多误区,能够很好的了解它,就能更好的学习假设检验. 从上述分析有如下结论:区间估计和假设检验可以应用于金融、医药、农业等各个领域;区间估计问题和假设检验问题可以相互转化;选择区间估计和假设检验方法时应该观察问题本身是否与样本信息相关联;显著性水平在两种统计推断方法起重要枢纽作用等.通过讨论,可以看出这两种统计推断方法在理论和实际中的应用都非常复杂,日常生活中,有些人对两种方法认识不够,存在个别误区;在解决一个实际问题时,并未首先关注问题的实质,以致于容易犯错.在处理任何一个问题时,均需要对两种方法足够熟悉,才能更好地避免犯错.统计学作为一门学科,但并非是一门独立的学科,它依赖于很多数学、计算机等专业知识;要想做好统计研究,必须具备丰富的专业知识以及较强的逻辑分析能力,不能一贯地参考经验,也不能一味地关注样本本身,要学会具体问题具体分析.通过本文的讨论,我们能够对区间估计和假设检验这两种推断方法更加熟悉和了解,能够将这两种方法应用于一些实际问题之中.3 理论论证
3.1 区间估计和假设检验的统计学意义
3.2 区间估计和假设检验应用
3.3 区间估计和假设检验的区别
3.4 区间估计和假设检验的联系
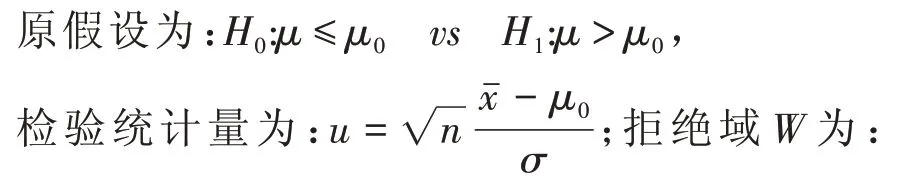



3.5 区间估计和假设检验的误区
4 例题论证:区间估计和假设检验关系举例
5 显著性水平的进一步讨论
5.1 显著性水平概念
5.2 两者关系
5.3 两类错误的关系及深度探究
6 结论和建议
