考虑可再生能源不确定性的最优潮流研究
2021-08-23王亭岭
李 鹏,王亭岭
(1.郑州电力高等专科学校,河南 郑州 450000;2.华北水利水电大学,河南 郑州 450045)
0 引言
潮流计算是电力系统规划和运行中的重要内容,直接影响系统的运行结果。而潮流优化是以优化某一目标为目的的计算,需要考虑等式约束和不等式约束。目前,可再生能源中以风电、光伏为代表的机组接入电网也给潮流优化带来了新的挑战,在考虑经济成本、环境成本和网络安全等因素后,潮流优化使得含有可再生能源的电网运行效果最优。
目前,针对可再生能源接入电网的影响研究比较充分。文献[1]针对光伏和风电互补性对高渗透率可再生能源集群接入规划影响进行了分析。文献[2]在分布式电源选址定容时考虑了负荷和分布式电源出力的时序波动性。文献[3]研究了考虑可再生能源出力概率模型和预测负荷区间模型的输电网规划方法。文献[4]针对基于配电网静态电压质量机会性约束的可再生能源分布式发电容量规划进行了分析。文献[5]研究了考虑可再生能源跨区域消纳的主动配电网多目标优化调度。文献[6]提出了一种高比例可再生能源电力系统的输配协同优化调度方法。
针对最优潮流,文献[7]提出了基于离散傅里叶变换矩阵的概率最优潮流计算方法。文献[8]考虑了风电资源的间歇性。文献[9]提出了一种计及风电置信风险成本的多目标最优潮流计算。目前,在最优潮流中计入可再生能源的不确定性研究的报道较少。
本文首先对最优潮流的数学模型进行了分析,针对风电、光伏和水轮机组建立了不确定性的模型,并对所建立的模型提出了最优潮流模型;然后以成本最小以及网损最小为目标函数,考虑功率平衡约束、潮流约束、节点电压约束、机组出力约束和网络安全约束,利用改进斑点鬣狗算法对模型进行了求解;最后对本文所提的模型和算法进行了仿真分析。
1 可再生能源不确定性建模
1.1 风机出力不确定性
考虑到风机出力完全依赖于风速,因此须要对风速的性质进行研究。实际工程中,风速分布选择Weibull概率分布函数[10],具体表达式如下:
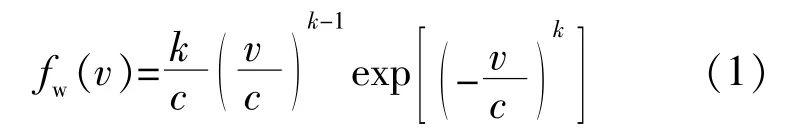
式中:v为风速,m/s;k为形状系数;c为尺度系数。
利用蒙特卡洛模拟得到的风速概率分布如图1所示。
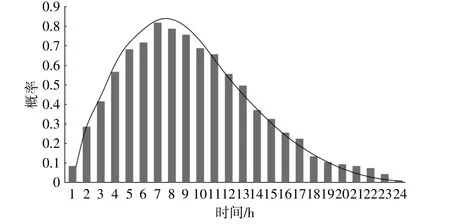
图1 风速概率分布Fig.1 Distribution of wind speed
工程上双馈感应式风机的实际出力PWi较为常用的计算方法如下:

式中:Pri为机组额定容量;vcin,vcout,vr分别为风速的切入、切出、额定值。
从式(2)可以看出,在风速低于切入风速或高于切出风速时,风机出力在某些区域会出现离散的情况,这类情况的概率函数为
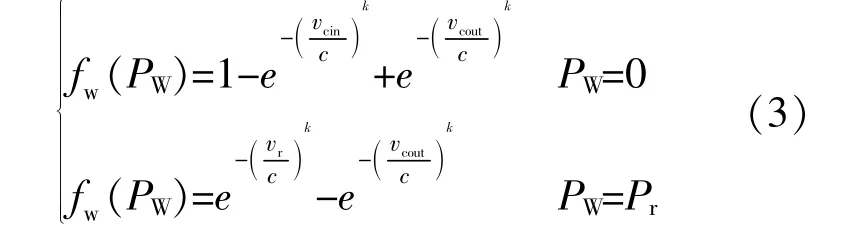
连续出力时的概率密度函数为

1.2 光伏出力不确定性建模
光伏发电依赖于光照辐射。工程上,日光照辐射强度G服从对数分布[11],具体表达式如下:

式中:μ,σ分别为光照辐射强度均值、标准差。
利用蒙特卡洛模拟之后的光照概率分布如图2所示。

图2 光照概率分布Fig.2 Distribution of solar irradiance
光伏太阳能板的出力计算式如下:

式中:Gstd为标准环境下光照辐射强度;RC为某辐射值。
1.3 水轮机出力
水轮机出力受到水流速度Qh和水头压力Hh的影响。Qh按照Gumbel概率分布,其概率密度函数为

式中:γ为尺寸参数;λ为位置参数。
水轮机的输出功率表达式为
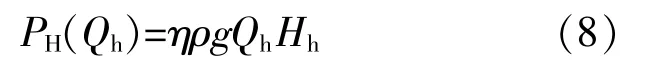
式中:η为水轮机效率;ρ为水量密度;g为重力加速度。
水流速概率分布如图3所示。

图3 水流速概率分布Fig.3 Distribution of flow rate
2 含可再生能源的最优潮流模型
2.1 传统最优潮流数学模型
最优潮流是一类优化问题,其数学模型如下:

s.t.

式中:f为目标函数;gk为等式约束;hl为不等式约束;x为状态变量;v为控制变量。
针对电力系统最优潮流,状态变量主要包括松弛节点有功、发电机节点无功、负荷节点电压和传输线功率;控制变量包括发电机节点电压、发电机节点有功、变压器分接头、并联电容补偿装置等。
考虑到可再生能源的不确定性,对上述模型进行扩展,将本文所提的不确定性计入目标函数和约束条件中,得到考虑可再生能源不确定性的最优潮流模型。
2.2 目标函数
可再生能源接入电网后,需要保持火电机组和可再生能源机组的总成本最小。其中传统火电机组的成本函数[12]为

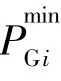
考虑到可再生能源机组的所有权,在运行时运行商支付相应的费用给机组的所有者,因此须要考虑这部分调度的直接费用,具体表达式如下:
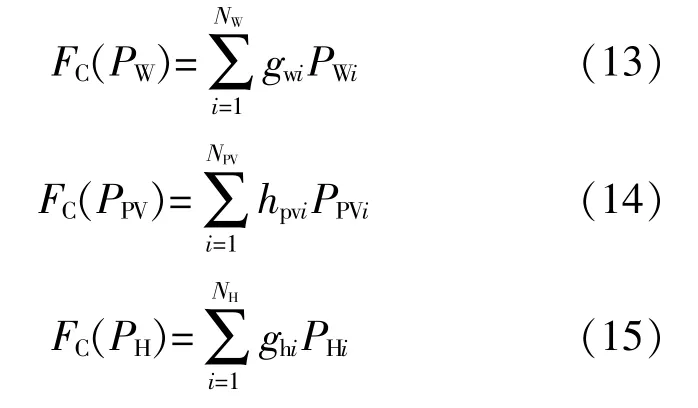
式中:PW,PPV和PH分别为风机、光伏和水轮机组的出力;gw,hpv和gh分别为风机、光伏和水轮机组的出力成本系数。
类似地,光伏和水电机组均会产生备用成本和罚成本。则全系统的总成本为

目标函数1为

目标函数2为系统中网损最小,表达式如下:
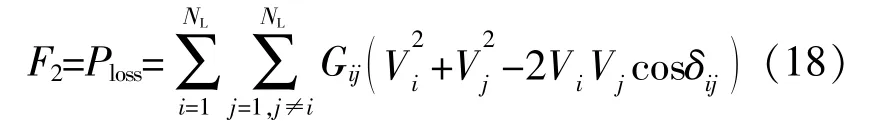
式中:NL为支路数量;Gij为ij节点之间支路电导;δij为节点ij之间电压角;Vi,Vj为节点i和j的电压;Ploss为网络损耗。
2.3 可再生能源不确定性在模型中的计及
考虑到这类机组的随机性和波动性,实际可用出力会与调度预想数据有偏差,因此调度中心须要留有一定备用容量。风机的备用成本表达式如下:
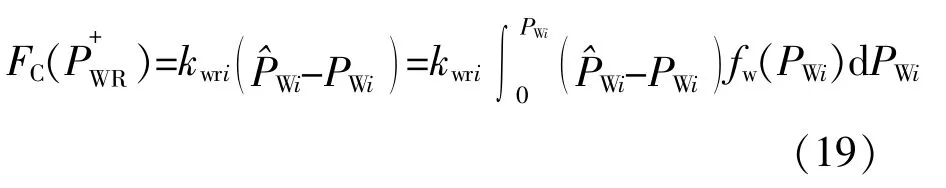
如果风机出力大于调度计划值,则调度中心须要削减火电机组出力,其罚成本为
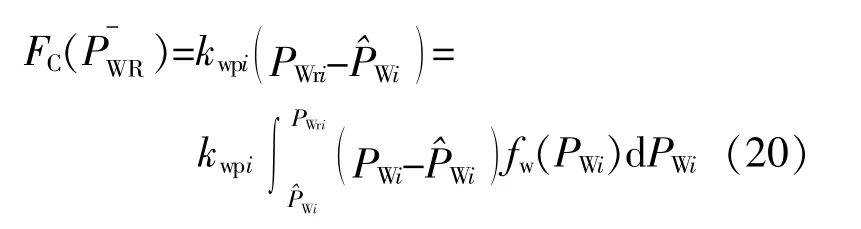
其他可再生能源的不确定性考虑方法与之类似。
2.4 约束条件
①功率平衡约束
等式约束主要指功率平衡约束,具体约束条件如下:
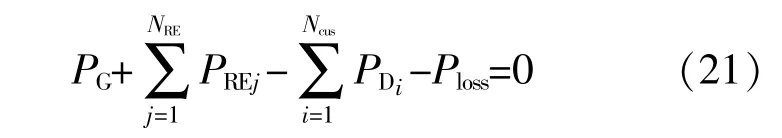
式中:PDi为节点i的负荷需求;Ncus为负荷节点数;PREj为第j个可再生能源机组出力;NRE为可再生能源机组数。
②潮流约束
潮流约束满足有功潮流和无功潮流平衡约束。
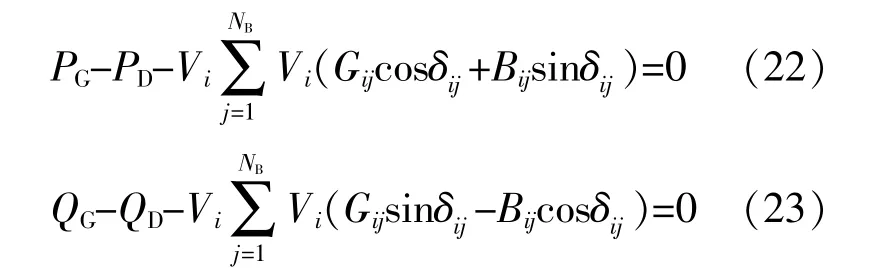
式中:QG为系统发出无功;δij为节点电纳。
③发电机节点电压约束
发电机节点电压约束保持网络节点电压稳定,具体表达式如下:
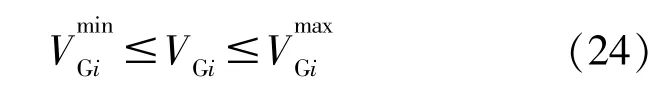
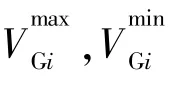
④机组出力约束
各机组的出力均应在限值之内。
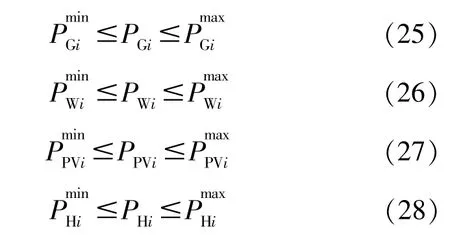
⑤网络安全约束
考虑到PQ节点的电压限制和线路热稳定极限,有:
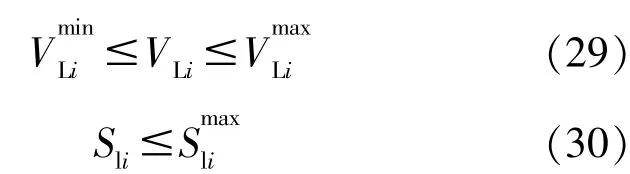
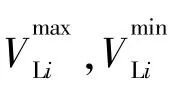
3 改进斑点鬣狗优化算法求解
3.1 斑点鬣狗优化算法
斑点鬣狗优化算法是模拟斑点鬣狗猎食行为的一种优化算法,考虑到斑点鬣狗的群居性、多重感官,对同一种族的关系进行内部排序,地位高的个体优先获得信任。其主要的捕食机制包括搜索、包围、狩猎和攻击。算法具体步骤如下。
①初始化
输入参数包括比例参数Gp和整体参数GI。
②生成随机数
根据初始化参数,生成随机矩阵:
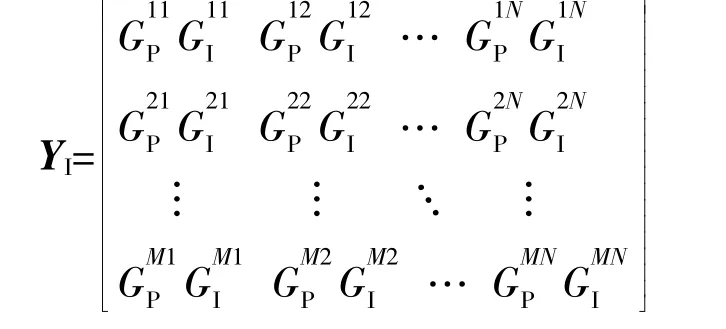
③适应度函数
目标行为R与时间T和误差信号E有关。

④位置更新
计算适应度值后要对鬣狗的实际位置进行估计,并判断与猎物的距离。

⑤围攻猎物
假设目标猎物为最佳选择,并且更新最佳位置。
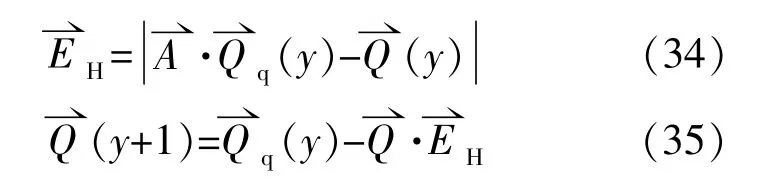
其中:

式中:rand1和rand2为0~1的随机数;I为迭代次数;Imax为最大迭代次数。
⑥捕猎
鬣狗捕猎的过程如下:

⑦攻击猎物
对猎物的攻击表达式如下:
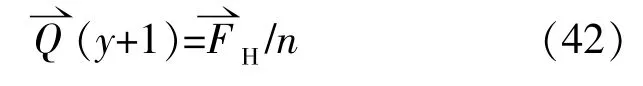
⑧搜寻猎物
鬣狗在范围内搜寻猎物,|D|>1时表示远离猎物;|D|<1时为靠近猎物。
3.2 改进斑点鬣狗优化算法
β函数是一种应用较广的分布函数,本文利用归一化函数加入混沌序列控制向量h。该向量作用于猎物搜寻阶段,从而提升算法的整体寻优性能。
①利用初始参数生成β混沌序列

②进行归一化


则归一化后的序列为

③计算任意时刻的序列值

3.3 求解流程
本文所提改进算法的求解流程如图4所示。
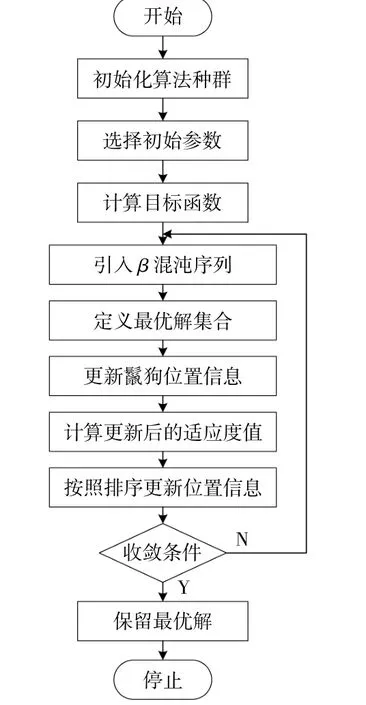
图4 算法流程图Fig.4 Flow chart of the proposed algorithm
4 算例分析
4.1 算例说明
本文选用IEEE 30节点系统[13]进行仿真,具体接线图如图5所示。该系统共有30个节点、6台机组和24个负荷节点。火电机组连接于1,2,5,8,11,13节点。为验证本文所提模型,将火电机组置于1,2,8节点,5节点为风机,11节点为光伏,13节点为水轮机组。则本文采用的系统共有30个节点、41条支路、6个发电机节点、24个负荷节点、11个控制变量(除松弛节点外所有发电机节点的有功出力和所有发电机节点的电压)。
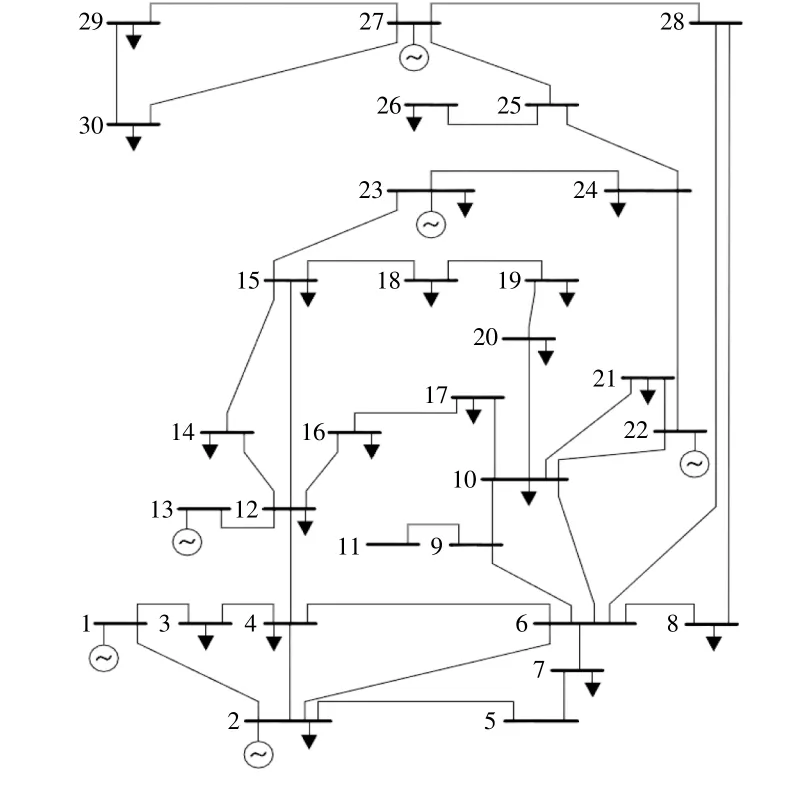
图5 IEEE 30节点图Fig.5 IEEE 30 bus feeder
对于风速不确定性,k=3,c=9;光伏的μ为6,σ为0.6。光伏额定功率为60 MW;风机额定功率为68 MW,切入、切出、额定风速分别为2.8,30,15 m/s。
针对本文所提算法,种群规模为50,最大迭代次数为150。
4.2 算例分析
利用本文所提算法进行分析,得到的潮流计算结果如表1所示。

表1 潮流计算结果Table 1 Results of optimal power flow
由表1可以看出,本文所提算法在求解网损和成本方面更优,相比粒子群(PSO)算法,总网损下降10%,总成本下降3.13%。
为了说明本文提出的改进算法的有效性,与PSO算法进行对比分析。同样选取网损最小、成本最小为目标,分别利用上述算法进行计算,结果表明,PSO算法求解耗时为38.36 s,本文所提算法求解耗时为29.66 s。
两种算法的网损、成本收敛情况分别如图6,7所示。
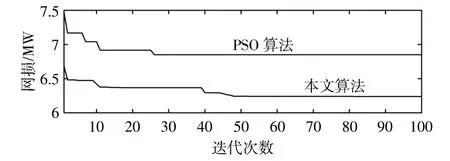
图6 两种算法的网损收敛情况Fig.6 Convergence comparison in two cases
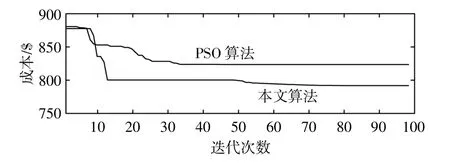
图7 两种算法的成本收敛情况Fig.7 Convergence comparison in two cases
可见,在收敛性和求解速度上,通过引入β过程进行优化,实现了在求解效率和收敛性上的改进。
5 结论
本文提出了考虑可再生能源不确定性的网络最优潮流模型。通过考虑可再生能源的不确定性,能够实现网络潮流的进一步优化。仿真分析表明,考虑可再生能源不确定性的网络潮流比原始网络潮流的成本和电压波动进一步降低,本文所提的算法能够在更短的时间内得到全局最优解,收敛性更好。
