基于迭代制导的运载火箭入轨级弹道设计及仿真
2021-08-23高家智陈小前
高家智,陈小前
(1.国防科技大学空天科学学院,长沙,410073;2.太原卫星发射中心,太原,030027)
0 引 言
迭代制导制导精度高、任务适应性强、箭上飞行软件简单、对地面诸元准备要求相对较低,在运载火箭上应用越来越广泛[1~3]。文献[4]针对主发动机推力为常值的情况,通过优化开关机时间来满足终端位置约束,引入权重因子提高迭代求解的精度;文献[5]针对多约束入轨条件,提出一种将迭代制导与数值积分相结合的轨迹预测制导方法,增加的推进剂的消耗在可接受范围之内;文献[6]在地心惯性系中建立航天器模型,以目标轨道要素为终端约束条件,得到一种简单有效的控件变轨迭代制导算法;针对飞行过程中发动机推力下降的重大故障,文献[7]基于迭代制导算法对弹道进行了重构,在完成故障识别和能力预测后,利用迭代制导将有效载荷送入预先设计好的救援轨道上去。
Boeing 公司针对阿波罗计划使用的土星5 运载火箭迭代制导方法的不足,开发了线性正切制导律(Linear Tangent Guidance,LTG),并在飞马火箭上升段入轨控制和离轨段返回控制中得到应用[8]。本文方法利用了其闭路制导律和预估公式,但制导计算的思路与文献提供的相反,引入了制导迭代变量,采用了根据初值求解两点边值问题的Newton-Raphson 方法。最后利用数值仿真验证了本文所设计方法的有效性。
1 最优控制问题及其制导律
在不考虑稀薄大气的情况下,火箭在真空段内的运动方程可表示如下[9]:

终端约束条件为

式中V,R分别为火箭在地心发射惯性坐标系中的速度和位置;G为重力矢量,G=-ω2R=-3R,其中,fM= 3.986 × 105km3s2为引力常数;ω为地球自转角速度;为秒流量;a为加速度的模,a=,其中,P为发动机推力,m为质量;Ue为有效排气速度;u为推力方向的单位向量。
定义哈密顿函数H和增广函数F如下:

这里的λ,α和β是拉格朗日乘子。
定义如下变量:
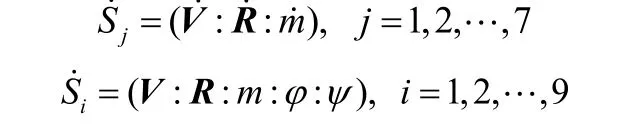
式中φ,ψ分别为俯仰角和偏航角。根据最优控制的必要条件有如下欧拉方程和横截条件:

由欧拉方程可解出:

式中uR=unit(R)为火箭质心地心矢径的单位向量。
由横截条件可得出:

相对于地球半径而言,火箭因推进引起高度的变化量是小量,并且λ与uR的夹角在90°附近,因此在式(8)中可忽略高阶向量,得:

该方程的解为

式中t为飞行时间;λK为定常单位向量;为定常速率向量;K为定常时间,一般情况下K≈Tgo2,Tgo为剩余飞行时间。如果是常值加速度,则K=Tgo2。
可以证明,对于圆轨道入轨时,下式成立:

即两矢量正交。
由于在迭代过程中,不断刷新K、λK和,为简便起见,省去下标K,即有:

考察式(13),存在如下特性:
b)如果采用地球平面假设,因为ω=0,则:

在本文的制导研究中,仍考虑地球是球体,且使用上述有关假设:
b)ω=λ˙;
c)忽略式(8)中的 3ω2(λ·uR)uR;
那么,制导律为

简化为LTG 制导律:

2 迭代制导的实现
2.1 端点状态预估
运载火箭的迭代制导属于复杂的两点边值问题,关机时刻火箭位置和速度的预估精度关系到迭代制导的精度、稳定性和鲁棒性。数值积分是一种精确的解决办法,但却是无法在箭上实时实现的办法,所以推导简化的解析代数公式就是一项根本任务。
在制导律式(15)的控制作用下,火箭在真空段的运动方程为

假设剩余飞行时间Tgo是已知的,且存在如下封闭形式的积分:

式中F1,F2,F3为待定系数。
积分式(18)有:

式中VD,RD分别为末端速度和位置矢量。
改写式(19)、(20),得到:
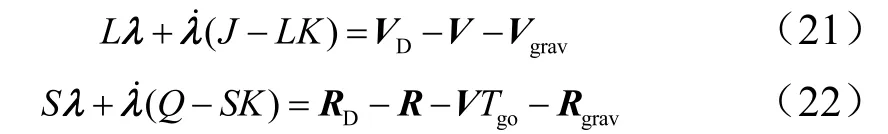
再积分式(17),得到:
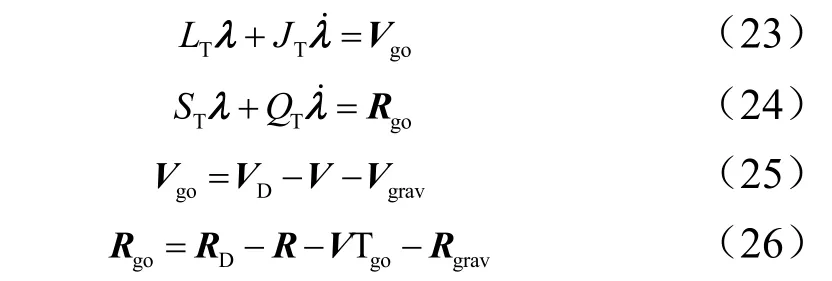
式中Vgo,Rgo分别为待增速度和位置矢量。
因此,如果已经知道λ和,就可以根据积分公式LT、ST、QT得出Vgo和Rgo,从而在当前位置R和速度V下,由制导律式(15)进行制导的端点的预估公式为

式中VP,RP分别为预测的末端速度和位置矢量。
2.2 纵平面迭代制导
运载火箭的欧拉角采用3-2-1 型表示的发惯系动力学方程组,可知只有侧平面的运动影响纵平面的运动,但纵平面的运动不会影响侧平面的运动,特别当偏航角很小时飞行控制可以解耦。因此可以先进行纵平面的迭代控制,再进行侧平面的迭代控制。
纵平面内的迭代控制采用标准入轨参数作为边界条件。这里的边界条件是采用极坐标边界条件而非直角指标边界条件,因为半长轴和偏心率与极坐标直接相关,所以在纵平面内的运动控制边界条件是满足标准入轨点对应的地心矢径、速度大小和当地速度倾角,这样就保证了椭圆轨道的半长轴和偏心率,加上侧平面的标准轨道跟踪导引,控制了zK和,理论上也是控制轨道根数的5 个变量。升交点赤经Ω主要由发射窗口的起飞时刻、火箭飞行时间和方位角决定,近地点幅角虽然是放开的,但跟踪Z通道的标准轨道这种约束本身也对第6 个轨道根数进行了隐式控制,这种方法一定程度约束了近地点幅角偏差的放大。
这里采用极坐标边界条件的另一个目的是提高迭代制导的鲁棒稳定性和收敛性,减小迭代制导结尾阶段的过早发散效应,三自由度制导仿真计算表明选择这种边界条件与视加速度反馈措施一起可以有效提高迭代制导的精度,使跳出迭代的剩余常值飞行时间小于0.5~1.0 s,几乎迭代至最后,提高了制导精度。
纵平面内的迭代控制采用 LTG 制导律方法,预测纵平面内关机时刻发惯系内的直角坐标参数Xp、、Yp和,然后进一步预测关机时刻的位置矢径Rp、速度大小Vp和当地速度倾角Θp,即:

迭代公式采用牛顿迭代法,即:

式中α,β为与俯仰角有关的制导变量。
因为采用了极坐标边界条件,没有显式解,校正计算需要采用3 变量的牛顿快速迭代法,涉及3×3 雅可比逆矩阵的实时计算,3×3 雅可比逆矩阵不需要数值计算,可以有解析表达式,并且因为上一步计算得到了的初值,下一步牛顿迭代计算只需一次就很精确,完全满足制导收敛精度。
由迭代解α,β,Tgo可以计算LTG 制导律的乘子向量λ和得到:

发惯系纵平面推力方向的单位控制向量:

记u=[u(1),u(2)]T,故当前时刻满足边界条件的俯仰姿态角应为

2.3 侧平面迭代制导
发射惯性系中的姿态角为俯仰角和偏航角为φ和ψ,初始质量m0,秒流量,轴向推力F在发射惯性系中推力分量表示为

动力学方程为

若偏航角为常值规律,火箭推力通常假设是常值,则推力的Z通道分量为常值,那么侧向通道在关机点的状态可以解析预测,即:

利用纵平面预测得到的纵向关机点状态和关机时间以及上述侧向通道关机点状态公式预测,可以进行轨道倾角i的解析预测计算,方法为:在纵向通道迭代计算完毕,预估纵向关机速度和位置,再根据上述常值偏航角和常值推力计算关机时的发惯系侧向速度和侧向位置,然后转换到发射地惯系计算轨道倾角,则i=i(ψ),根据轨道倾角期望值ic,容易单变量迭代求解偏航角指令。
那么对偏航角进行迭代满足所要求的轨道倾角属于单变量迭代,很容易快速求解。
3 仿真结果及分析
仿真起始条件为:发惯系下起滑点及第3 级关机点参数X=593 125.71 m,Y=184 422.32 m,Z=-77 388 m,VX=6676.607 m/s,Vy=648.986 m/s,Vz=-286.533 m/s,标准点火时刻532.3 s,推力28 000 N,初始质量1206.3 kg,秒耗量10 kg/s,标准滑行时间303.7 s[10]。
目标卫星轨道参数为:半长轴a=6860.788 km,偏心率e=0,轨道倾角i=97.3 °。
制导精度要求:半长轴偏差小于1 km,偏心率偏差小于0.0001,轨道倾角偏差小于0.01°。
经过仿真计算,发惯系位移及速度变化情况见图1所示。

图1 发惯系位移及速度变化情况Fig.1 Position and Velocity Changes in Launch Inertial System
俯仰角、偏航角以及其它参数变化曲线如图2 所示,滑行轨道、迭代制导轨道与运行轨道的放大图如图3 所示。输出结果如下:半长轴6860.768 km,偏心率0.000 012,轨道倾角97.3072°,制导时间49.35 s,升交点角距163.42°。可见长半轴误差20 m,偏心率偏差0.000 012,轨道倾角偏差0.0072°,均满足制导精度要求。
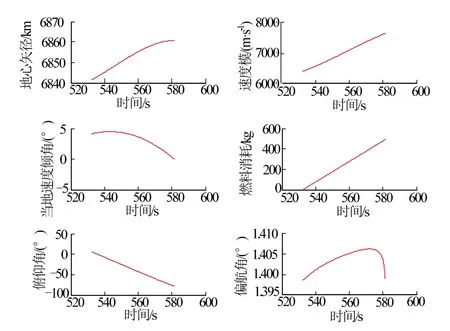
图2 主要飞行变量变化情况Fig.2 Major Flight Variable Variations

图3 滑行轨道、迭代制导轨道及运行轨道放大图Fig.3 Enlarged View of Dragging Track,Iterated Guidance Track,and Orbit
4 结束语
本文对多级运载火箭入轨段的迭代制导方法进行了较为深入研究,从仿真结果来看本文所提出的入轨级迭代制导方法制导精度高,且计算简单、易于实现。
